Effect of 3-D step topography on ground motion
-
摘要: 运用谱元法模拟了不同类型三维台阶地形对点源地震动的影响, 发现在中小地震中, 大型山系边缘的三维台阶地形对地表地震波具有一定的影响. 台阶斜坡与上水平地层交线和下水平地层交线的影响作用各不相同. 通过地表接收到的地震动描述了各种不同地形的波形快照特点, 并且通过绘制的台阶斜坡与上水平地层交线及下水平地层交线的测线图, 发现波形相对于水平地形有明显的后续波. 同时发现, 台阶地形上下测线相对于水平地形具有放大作用.下测线波形放大倍数基本在1.1—1.5, 上测线放大倍数在0.9—1之间. 通过描述山体边缘台阶结构在点源地震中产生的影响, 定量计算了三维台阶不同角度各个位置相对于水平地形的放大倍数, 为以后工程研究提供一个依据.Abstract: This paper simulates the different types of three-dimensional step topography effects on ground motion due to a point source by using spectral element method. Level topography and several different 3-D step topographies are simulated, which shows that the 3-D step topographies have an important impact on seismic waves. The effect from the intersecting lines of step slopes with upper level is different from that with the lower level. Moreover, the characteristics of various topographies are described using snapshots of the ground motions; the measuring line diagrams of the intersecting lines of step slope with upper level and those with the lower level demonstrate that the waveform diagrams of 3-D step topography have obvious scattering waves relative to level topography. Also it shows that the values on the upper and lower measuring lines on 3-D step topography are amplified relative to level topography. On the waveforms of lower measuring lines the amplification ranges from 1.1 to 1.5, and that is from 0.9 to 1 on the waveforms of upper measuring lines. These studies describe the impact of step topography at the edge of the mountain due to a point-source earthquake and give the respective positions’magnification of the 3-D step topography relative to level topography, providing a basis for forward engineering studies.
-
引言
大量的观测资料及研究表明，地表地形对地震动有重要影响，地表凸起地形和小山包顶部的震害更为严重． 例如，1970年云南通海地震震后分析结果显示，局部孤突地形震害明显，比平缓场地明显高1倍左右； 1988年云南澜沧-耿马地震，大部分高烈度点位于孤立凸起地形上(周正华等，2003)． 地震工程学已经定性地认识到孤突地形会产生更加严重的震害，但是对于山体的边缘部分，现在的研究还不是很多． 山体边缘地形对于地震动的影响研究具有非常重要的意义，也是本文旨在研究的问题. 随着我国经济建设快速发展，一些大型工程项目的实施等，不可能都建在平原上，部分区段将不可避免地建造在山地和斜坡，如何了解各种不同地形对震害的影响，成为迫切研究的问题． 本文将山体边缘地形简化为台阶地形进行研究． 由于实际地形中标准的台阶地形是十分少见的，更多的是台阶存在各种凹凸，因而研究三维台阶地形对地表地震动的影响更为重要.
在宏观调查中发现，特殊地形区域(山脊、 河谷、 陡坎、 悬崖等)处的建筑物的烈度异常，通过地形观测台阵系统研究地震动的影响，获得了大量的观测数据，进一步确定了地表局部地形对于地震动的影响(王伟，2011)． Boore(1972)通过对1971年2月9日San Fern and o地震中Pacoima大坝上记录的地震动加速度进行分析发现，坝上地震动在任何周期上的加速度与没有地形效应影响的记录对比有25%—50%的差异. 但是由于实际地形的特殊性，以及地球内部介质的复杂性，很难将这种影响简单归为是单一的地形造成的影响，因此这就需要寻求一种理论的方法，单独将地形提取出来进行对比，了解地形具体对于地表地震动造成了哪些影响，这就需要用数值模拟方法来进行计算研究. 数值模拟方法主要包括有限差分法、 有限元法、 伪谱法和谱元法. 有限差分法计算效率高，占用内存小，并且空间离散化简单． 有限差分法可以精确地模拟三维复杂介质(如沉积盆地、 断裂带、 俯冲带等)中的地震． 但是这种方法灵活性差，处理不规则界面问题能力差. 特殊自由表面条件需要特别处理. 尽管坐标转换(Jih，et al，1988)和网格变形法(Tessmer et al， 1992； Tessmer，Kosloff，1994)取得了相当的成功，但这使得地下复杂介质的边界扭曲变形，影响了研究. 特别是对于动态破裂问题，破裂面位错的不连续与计算节点很难一致. 有限元法满足自由表面条件，灵活性强，可以处理任意形状的介质. 但是这种方法计算效率很低，内存需要大，网格剖分复杂耗时. 伪谱法(Tessmer et al， 1992； Tessmer，Kosloff，1994; Wang et al， 2001)是一种全局方法，但由于其全局性，妨碍它的并行化，限制了在大规模计算中的应用. 谱元法是一种加权余量的方法，被Seriani等(1992)首次应用于地震波传播模拟运算当中，目前已经成功应用于二维和三维弹性介质地震波传播问题(Komatitsch，Vilotte，1998; Komititsch，Tromp，1999)． 然而通常的Legendre谱元法对于更为复杂的边界，不能采用结构化网格划分． 而非结构化网格剖分必须引入三角单元谱元理论，三角单元理论比四边形单元更为复杂，且效率和精度降低． 对此，周红和陈晓非(2007)提出了交叉单元的Legendre谱元法，保留了结构化网格的优势，同时又可以处理更为复杂的边界问题． 这种方法应用范围广泛，计算效率高，为地震波模拟提供了非常有效的方法.
局部地表地形对地震动的影响已经引起了研究人员的广泛关注，并且进行了大量的研究试验工作(袁晓铭，廖振鹏，1996; 薄景山等，2003; 董良国，2005; 王海云，谢礼立，2010; 胡元鑫等，2011)． Boore(1972)使用有限差分法计算了SH波入射下简单山体地形的地震动反应特征． 结果表明，当入射地震波波长与地形特征尺寸相当且坡度相对较陡时，地形对地震波的影响与频率相关，而且地震动大小会有放大、 缩小的变化． 研究发现，山体地形地震动的放大系数与平坦场地放大系数具有75%的差异. 刘晶波(1996)运用有限元法结合修正的透射人工边界，研究了二维不规则地形中P波，SV波和瑞雷波传播对地面运动的影响． 结果表明，瑞雷波传播时孤突地形对地面运动的放大作用显著大于P波和SV波，相邻不规则地形的存在使地面运动进一步放大，持时延长． 陈丙午(1982)提出了“双向剪切变形”的有限元模型，将三维问题简化为二维，对典型震害实震进行模拟，研究了山体地形及参数对地震动的影响． 景立平等(2005)采用显示集中质量有限元与透射边界相结合的方法，研究复杂场地对地震波传播的影响． 周红(2007)、 周红等(2010)利用局域离散波数法计算了地形与地震频率的关系，并计算了多组不同地形对面波的影响． 上述模拟结果均观测到了地表凸起和小山包顶部地震动增强的效应. 荣棉水和李小军(2007)、 荣棉水等(2009)利用显示有限元有限差分方法进行了二维场地地形影响分析，发现地形的特征尺寸和入射角对地震动的峰值和谱特性均有影响.
本文运用谱元法模拟不同类型三维台阶地形对点源地震动的影响. 大型山脉的两端地形可简化为具有各种凹凸的三维台阶地形. 本文以点源地震为例，运用谱元法，构造了多种不同的三维台阶模型，模拟地表地震波场，绘制了地表接收的速度波形快照，三维台阶地形中斜坡与上水平面交线(上测线)和下水平面交线(下测线)的波形图，并且计算了各种三维台阶地形相对于水平地形速度和加速度的放大倍数，以此来研究山体边缘不同三维台阶对于地震动的具体影响. 目前大部分地形效应研究都是基于二维地形模型进行的，并且主要是针对地表单个小规模的凸起凹陷地形进行． 而针对大型山系的三维地形影响的研究目前还很少． 本研究对于进一步认识三维台阶地表地形对地震动的影响具有重要意义，并为工程选址提供参考.
1. 谱元法简介
本文通过Legendre谱方法模拟山体边缘不同台阶地形对地表地震波场的影响. 下面对该方法进行简单的阐述(周红，2007).
对于地下介质中传播的地震波，可以由波动方程、 初始条件和边界条件来描述，即在Ω中地震波位移满足方程
式中，u是位移向量，σ是应力张量，C是刚度张量，ρ是密度，f是外力，T表示转置，“∶”表示张量相乘，u上的点表示时间微分.
在谱元法中，方程(1)点乘任意试验权函数w，并且分步积分，得到方程为
式中，Ω是物理计算域，Γ是它的边界，包括自由地表边界Γf和人工吸收边界Γabs． 由于地表应力为零，Γf在部分过程中消失，因此上式自然满足地表条件.
Legendre谱元方法在具体计算过程中，首先将计算区域离散划分为不重叠的四边形(二维)或六面型(三维)小单元，并利用局域坐标将小单元Ωe映射到规则的考察区域[-1，1]nΛ上. 在参考单元Λ中，引入N阶多项式的基函数，它在单元Ωe上对应一组节点，uNe和wNe是u和w在这些节点上的Legrange插值. 这些节点在[-1，1]区间内取为Gauss-Lobatto-Legendre点，它们是方程
的根. P′N(ξ)是Legendre N阶多项式的偏导数. 在参考单元Λ中，ueN表示为
式中，h(ξp)表示p项一维Lagrange插值，在点ξ=ξp为1，在其它点ξ=ξp，q≠p等于0. 一旦引入多项式近似，方程(2)的积分利用Gauss-Lobatto-Legendre积分规则得到
式中，wi是积分系数，Ji是Jacobian矩阵，由影射Ωe到Λ的关系Γe决定. 空间离散化后，进行时间离散化，用U表示介质位移未知量，得到
式中，M是质量矩阵，K是刚度矩阵，F是源项. Legendre 谱元的不重叠单元的空间离散，以Gauss-Lobatto-Legendre节点插值多项式，结合Gauss-Lobatto-Legendre积分规则，使得质量矩阵M为对角线矩阵，K为带宽矩阵． M的对角性使得谱元法的计算效率较有限元法有了较大提高．
2. 模型计算与分析
对于大型山系两端以及高原抬起部分，可以简化为台阶地形． 同时由于实际地表地形的复杂性，并不存在非常规则的台阶地形，因此为了使得研究结果更加接近于实际地形，选取了不同的三维台阶地形模型来进行研究.
按照上述方法，首先设计了一个长宽深为60 km×55 km×50 km的计算区域. 建立空间直角坐标系，将计算区域置于坐标系中，长、 宽、 深分别对应x，y，z轴． 其中台阶起始处位于计算区域x=18 km处，台阶倾角为π/4，台阶垂直高度为4 km，尖凸在倾斜面的跨度为8 km. 在3种模型中，震源位置均位于35 km、 22 km和5 km处，这样可以使得地表接收点远离极震区，以排除极震区波场效应的影响. 对介质进行标准化处理后各介质参数为ρ=1，λ=μ=1，地震波频率f=1. 对3类地表地形进行模拟，包括水平地形、 简单台阶地形、 三维台阶地形． 其中三维地形主要研究斜坡面存在的尖凸、 尖凹、 圆凸和圆凹4种情形． 这主要是由于实际地形的复杂性，台阶边缘存在各种不同大小的凸凹，如图 1所示.
![]()
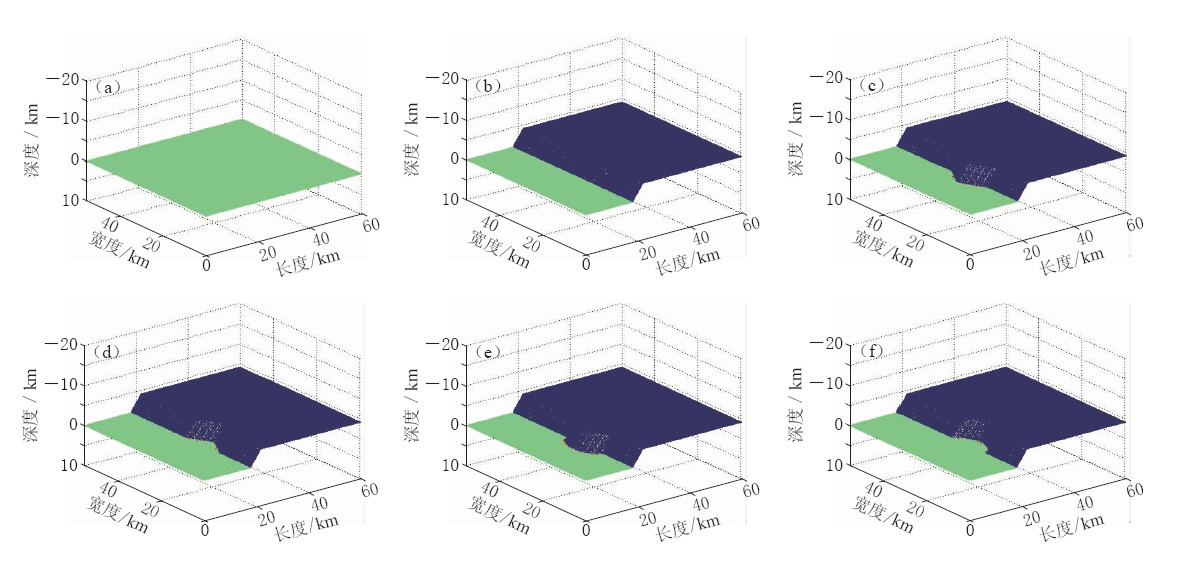
图 1 三类地形模型 (a) 水平地形； (b) 简单的二维阶梯地形； (c) 有尖凸的阶梯地形； (d) 有尖凹的阶梯地形； (e) 有圆凸的阶梯地形； (f) 中间有圆凹的阶梯地形Figure 1. The three types of terrain models (a) The level terrain； (b) The terrain with a simple step； (c) The step terrain with a sharp convex； (d) The step terrain with a sharp concave； (e) The step terrain with a rounded convex; (f) The step terrain with a rounded concave为便于观察，使各个地形中震源正上方同时接收到地震波，在水平地形中，震源位置为35，22和9 km，这样方便对比研究. 通过并行计算，模拟了6种模型在地表x向的速度波形快照，并且分析研究了各种模型对于点源地表地震动的影响，如图 2所示.
![]()
图 2 对应图1(a)—(f) 6种地形的地表x分量速度7—9 s快照Figure 2. Snapshots of x-component velocity waveforms on the surface position corresponding to the six types of terrains in Figs.1(a)-(f) ranging from 7 s to 9 s图 2中每个时间切片中的6个小图分别与图 1中的6个地形一一对应． 从图中可以清楚地看到不同的地形对于地表接收到的地震波形有明显的影响，总体上由震源正上方向周围扩散． 由于震源位于地形变化的对称线(y=22 km)上，使得波形快照上下对称. 由于地形差别，不同地形的波形图略有差别. 通过不同地形对比，可以观察到以下现象.
1)水平地形(图 1a)与简单台阶地形(图 1b)对比，发现9 s时地震波初动达到了台阶地形斜坡位置． 由于斜坡距离震中位置更近，先于水平地形接收到地震波，并开始向各方向传播，由此在地表接收的波形图的斜坡位置出现了弧形圆凸.
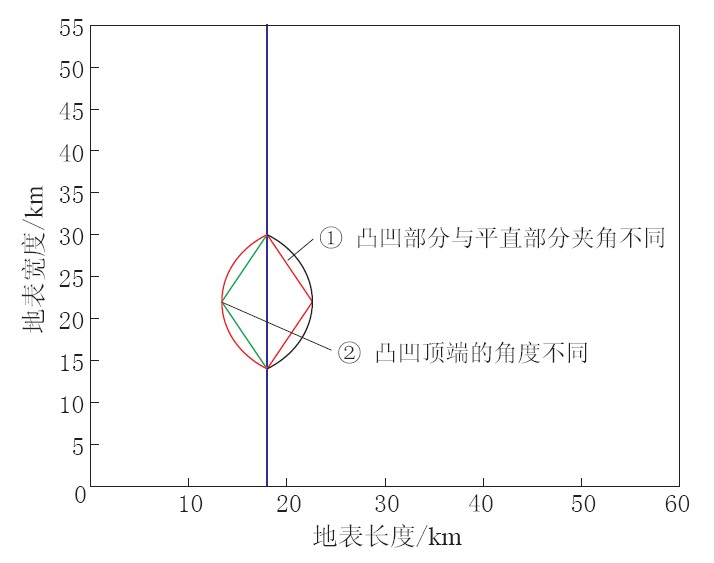
2)水平地形(图 1a)与具有尖凸(图 1c)和圆凸(图 1e)地形对比，发现11 s地震波初动已经到达了台阶地形的斜坡处，波同时传播到台阶的斜坡处． 但是由于地形的差别，速度波形快照图在尖凸的斜坡处形成圆弧，而在圆凸地形的斜坡处形成了一个尖锐的凸起，这与地形斜坡凸起的拐角有关(如图 3中①所示)． 随着时间推移，速度波形快照趋于一致．
3)水平地形(图 1a)与具有尖凹(图 1d)和圆凹(图 1f)的地形对比，发现7s时波形已经传播到斜坡的凹处的顶端； 在尖凹处，形状比较尖锐； 在圆凹处，形状比较圆润． 这是由于凹处顶点的形状不同所致(如图 3中②所示)． 随着时间推移，波形趋于一致.
![]()
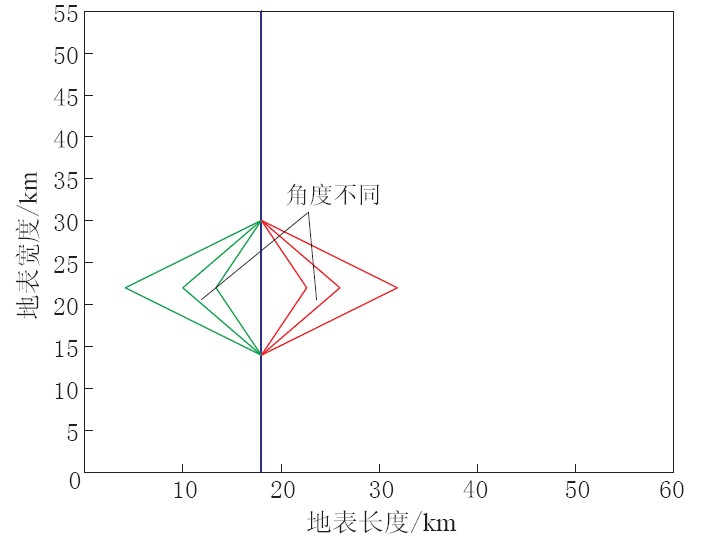
图 3 台阶下测线 蓝色、 绿色、 黄色、 红色、 黑色分别 对应图1中(b)—(f)的地形Figure 3. The lower lines of steps Blue, green, yellow, red, black lines correspond to the terrains in Figs.1(b)-(f), respectively因此，不同形状的台阶地形对于速度波形的影响主要体现斜坡凹凸的形状及顶角的角度，如图 3和图 4所示. 当台阶没有凸凹时，波形首先到达斜坡处后，由于震源距离不同，速度波形快照出现了凸起． 随着时间推移，当波通过斜坡后，又以与水平地形相同的规律向后传播． 当斜坡出现凹凸形状时，波形发生了变化． 这种变化主要与凹凸的各个拐角的大小有关. 当拐角较小时，速度快照出现尖锐的凸起； 当拐角较大时，速度快照出现圆润的凸起. 其中y方向与z方向的速度波形快照规律与x方向规律基本一致，不再赘述.
![]()
图 4 不同角度台阶下测线 绿色、 红色分别对应图1中(c)、 (d)不同角度的地形Figure 4. The lower lines of steps with different angles Green and red lines correspond to the terrains with different angles in Figs.1(c) and 1(d), respectively为了更好地研究大型山系边缘凸凹地形在中小地震中的影响，模拟了地表接收到的x方向速度峰值图，如图 5所示． 图 5中各模型分别为水平地形及图 4所示从左到右的7个模型，依次为水平地形，尖凸台阶地形(图 1c)中夹角分别为60°，90°和120°情形，简单台阶地形(图 1b)，及尖凹台阶地形(图 1d)中夹角为120°，90°和60°的情形.
![]()
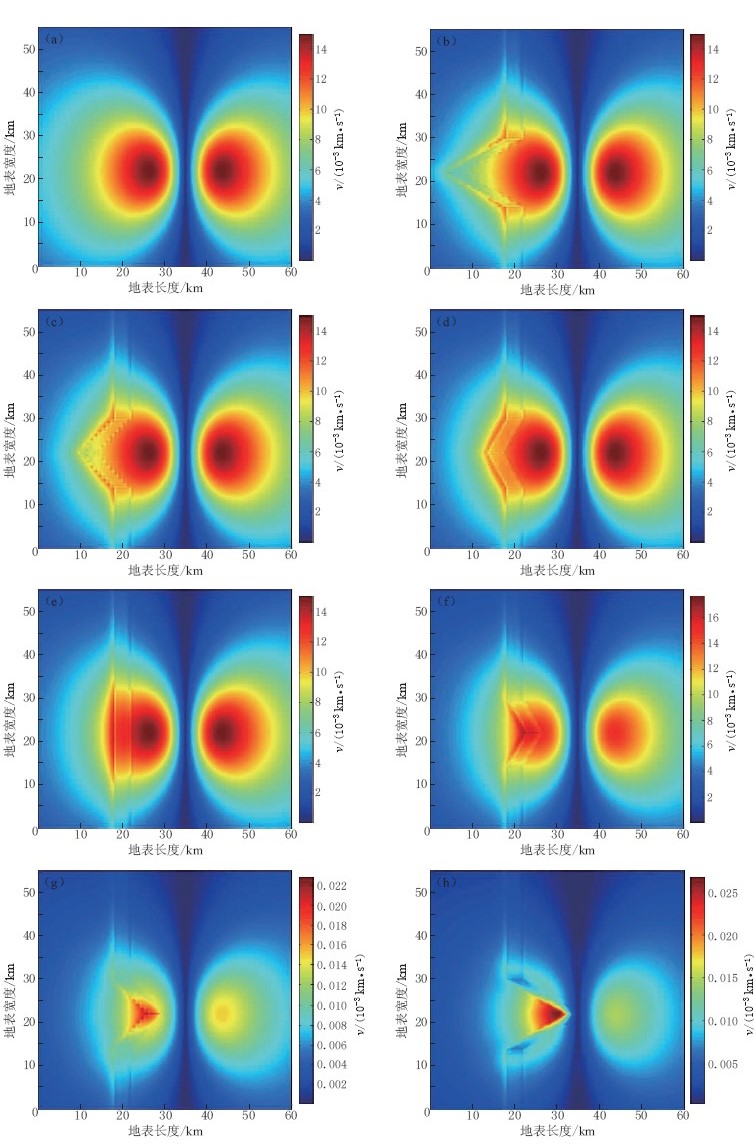
图 5 各个模型地表接收到的狓方向速度峰值图 (a)水平地形;(b)夹角为60°的尖凸地形;(c)夹角为90°的尖凸地形;(d)夹角为120°的尖凸地形; (e)简单台阶地形;(f)夹角为120°的尖凹地形;(g)夹角为90°的尖凹地形;(h)夹角为60°的尖凹地形Figure 5. The x-componet peak velocities observed on the surface of each model (a)Thelevel terrain;(b)The terrain with 60° sharp convex;(c) Theterrain with 90° sharp convex;(d) The terrain with 120° sharpconvex;(e) Simple two-dimensional step terrain;(f) The terrain with 120°sharp concave;(g) The terrain with 90° sharp concave;(h) The terrain with 60° sharp concave从图 5中可以清楚地看到，台阶斜坡与上地表交线(上测线)附近变化不大，斜坡处的峰值减小； 而下水平面接近于台阶斜坡与下地表的交线(下测线)附近的值有比较明显的放大作用． 对于尖凸地形(图 1c)，放大作用主要出现在图 3中①的位置附近，并且沿着图 3中①—②位置的测线，放大作用逐渐减小. 对于图 1d，放大作用主要出现在尖凹的下测线顶点处，并且随着向两侧延伸，放大作用逐渐减小.
为了观察地形台阶处接收到的速度波形的差异，单独提取了上测线和下测线的速度波形图，如图 6所示．
![]()
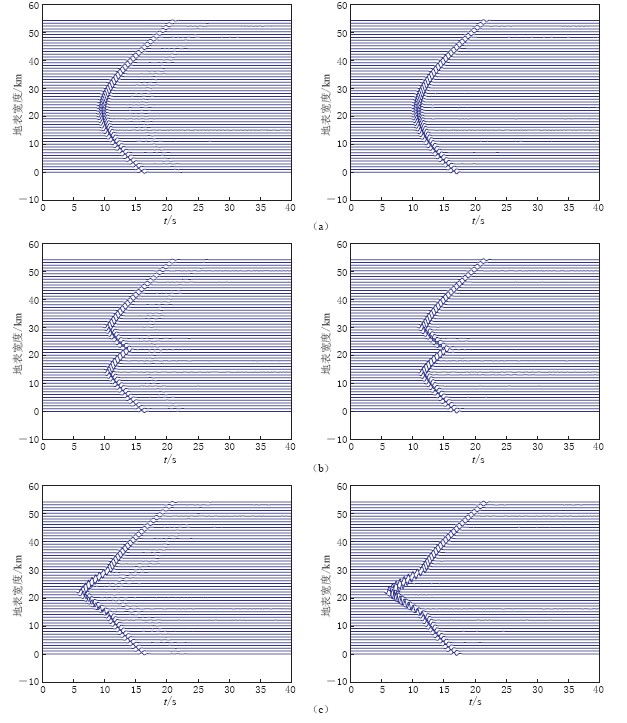
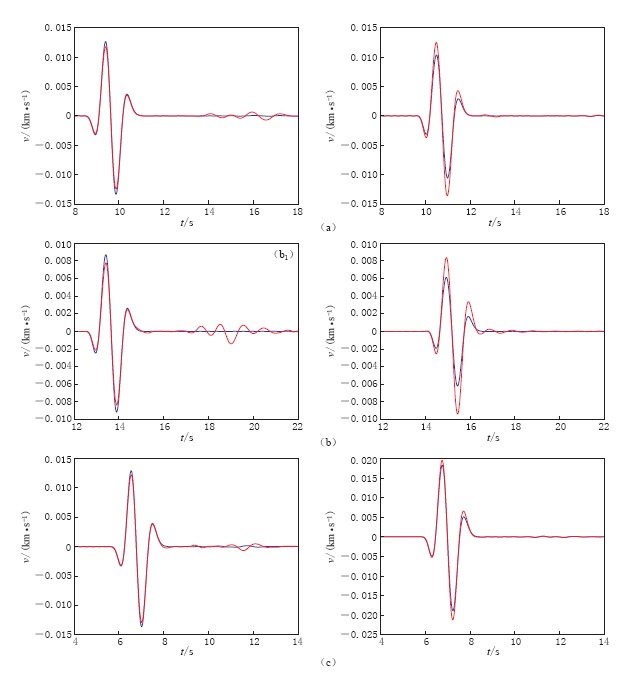
图 6 台阶端线x分量波形图(左侧图为上测线波形， 右侧图为下测线波形) (a) 简单二维台阶地形波形； (b) 尖凸台阶地形波形； (c) 尖凹台阶地形波形Figure 6. The x-component velocity waveforms (the left panels are waveforms measured on upper line， and the right ones are measured on lower line) (a) The diagram of the simple two-dimensional step terrain； (b) The diagram of the step terrain with sharp convex； (c) The diagram of the step terrain with the sharp concave图 6中左侧为上测线x分量速度波形图，右侧为下测线速度波形图(波形放大了100倍)． 其中图 6a为图 1b对应的地形； 图 6b为图 1c对应的地形，尖凸夹角为90°; 图 6c为图 1d对应的地形，尖凹夹角为90°. 从图 6a中可以看到，震源在测线上的投影点首先接收到地震波，然后逐渐向两侧依次接受地震波，振幅中间最大． 随着距离震中越来越远，振幅逐渐减小，其中上测线与下测线无明显差别． 图 6b中尖凸两侧与拐点(图 3中①的位置)首先接收到地震波，依次向两侧传播，随着距离越来越远，振幅越来越小，其中振幅最大值出现在尖凸两侧拐点处，上测线振幅略小于下测线振幅． 图 6c中尖凸地形中，尖凸的顶点最先接收到地震波，两侧振幅越来越小，振幅最大值出现在尖凸的顶点处，可以明显地看到下交线的振幅略大于上交线的振幅. 为了细致地看到波形的变化，提取各图中震源在上测线和下测线投影点的速度和加速度波形图． 为了消除震源到接收点距离不同的影响，以上测线与上水平地形重合的地形为参照，下测线选取了与下水平地层重合的地形为参照，如图 7、 图 8所示． 图中红色表示台阶地形投影点的x分量速度波形，蓝色表示水平地形对应点的x分量速度波形． 图 7—8中a，b，c分别与图 6中相应的图形对应． 通过观察发现，地形对上测线和下测线具有不同的影响． 上测线直达波峰值相对于水平地形略有减小，但在直达波之后开始出现了小的振荡； 下测线直达波相对于水平地形具有放大作用，直达波之后几乎没有振荡出现. 由此可见，具有三维地形的情形对波形的影响体现在两个方面，即振幅和后续波． 振幅在上测线上相对水平地形缩小，下侧线相对水平地形放大； 后续波则是主要在下测线影响比较大. 速度波形图与加速度波形图一致. 以上图形均以水平向的波形图为例，通过绘图，发现另外两个分量具有类似的规律，故不赘述.
![]()
图 7 震源在上测线(左侧图)和下测线(右侧图)投影点的x分量速度波形图 图(a)， (b)， (c)分别为图6(a), (b), (c)中震源在上下测线投影点的速度波形Figure 7. The x-component velocity waveformｓ of the projected point of the source on the upper (left panels) and lower (right panels) lines Figs.(a), (b), (c) separately correspond to the velocity waveforms projected on the point from the source to the survey line in Figs.6(a), (b), (c)![]()
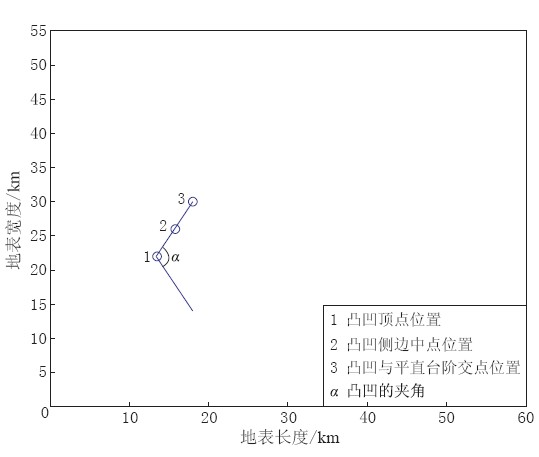
图 8 震源在上测线(左侧图)和下测线(右侧图)投影点的x分量加速度波形图 图(a)， (b)， (c)分别为图6(a)， (b)， (c)中震源在上下测线投影点的加速度波形Figure 8. The x-component acceleration waveforms of the projected point of the source on the upper (left panels) and lower (right panels) lines Figs.(a), (b), (c) separately correspond to the velocity waveforms projected on the point from the source to the survey line in Figs.6(a), (b), (c)通过上述各类图形可以明显地看到三维台阶地形对于地表地震波的影响． 对于尖凸台阶，这种影响主要体现在尖凸顶角的大小(图 4)． 这主要是由于当顶点的角度比较小时，两侧斜坡距离震源更近，更快地接收到地震波． 而对于尖凹台阶地形，则是当顶点处夹角比较小时，顶点距离震源更近，更快地接收到地震波，所以形成了图 4中的波形. 另外由于台阶地形中尖凸和尖凹的存在，使得地震波反射，形成了波形内部的小振荡． 这种振荡尖凹地形作用明显于尖凸地形，顶点处角度大的明显于角度小的地形. 为了更好地研究地形对于波形放大缩小的作用，选取了几个特殊点，将其与水平地形波形峰值进行比较，来观察三维地形效应的速度波形和加速度波形的放大倍数，如表 1、 表 2所示． 表中所述位置在图 9中进行了说明.
表 1 三维台阶地形与水平地形速度峰值比较(放大倍数)Table 1. Comparison of the peak velocities of three-dimensional step terrain with those of the horizontal terrain (magnification)
表 2 三维台阶地形与水平地形加速度峰值比较(放大倍数)Table 2. Comparison of the peak accelerations of three-dimensional step terrain with those of the horizontal terrain (magnification)
![]()
图 9 表1和表2中测点位置Figure 9. Distribution of the measuring points listed in Tables 1 and 2从表 1中可以看到，台阶地形下测线速度波形放大倍数基本为1.1—1.5，上测线放大倍数为0.9—1． 上测线的速度波形峰值相对于水平地形缩小了，但是变化非常小，在0.9—1之间浮动，其中三维尖凸角度大小对于波形放大倍数影响没有明显差别； 下测线的波形峰值相对于水平地形放大了，放大倍数相对于上测线变化比较大，基本为1.3左右． 同时可以观察到，这种放大倍数随着α角度的变化在变化，随着α的增大，放大倍数逐渐缩小. 同 时，位置2测线峰值的放大倍数大于位置1和位置3. 表中两个斜体的数据变化比较大，其原因是由于网格不是均匀划分，所选位置的特殊性所致. 从表 2可以看到，台阶地形下测线加速度波形放大倍数基本为1.1—1.5，上测线放大倍数为0.9—1． 加速度波形放大倍数规律与速度波形放大倍数规律比较一致.
通过上述观察，三维台阶地形对地表波形有一定的影响，这种影响在台阶上部和下部具有不同的体现，在上测线主要体现在波形变得复杂，有后续波出现，而峰值无明显变化； 在下测线主要体现在峰值的变化上，波形的形状无明显变化． 对于具体放大倍数，见表 1、 表 2所列.
3. 讨论与结论
我们运用谱元法，模拟了不同类型三维台阶地形对点源地震动的影响，绘制了地表接收的速度波形快照和台阶与地表交线的测线图． 结果表明，三维台阶地形结构对于地震动具有一定影响，主要体现在波形和振幅上的变化． 由于地形作用，使得地表地震波出现了明显的后续波，而这种后续波在水平地形中是观察不到的． 同时主波的振幅相对于平层地形也有变化，台阶地形下测线波形放大倍数基本为1.1—1.5，上测线放大倍数为0.9—1． 此结果为以后的工程研究具有一定的参考意义．
中小地震在模拟中可以将震源简化为点源，而三维台阶地形模型是各大型山系的两端地形的简化，因此，本研究代表了大型山系两端以及高原抬起部分地形在中小型地震地表地震动的影响. 在此类研究中，在进行中小地震及大型山系模拟时，在对台阶上下测线的处理时，可以根据其三维模型凸角不同乘以一个系数，以此将其当成水平地层处理． 本文描述大型山体边缘台阶结构在中小型地震中产生的影响，并且定量计算了三维台阶凹凸角度各个位置相对水平地形的放大倍数，其结果可为以后地震安全性评估提供一个参考．
本文所做的研究是针对大型山系边缘三维地形情况，在中小地震中的影响，具有一定的特殊性． 对于山体中部，在中小型地震和大地震中的影响，以及频率在山体地形中的影响，将在后续的研究中逐步进行报道.
-
![]()
图 1 三类地形模型 (a) 水平地形； (b) 简单的二维阶梯地形； (c) 有尖凸的阶梯地形； (d) 有尖凹的阶梯地形； (e) 有圆凸的阶梯地形； (f) 中间有圆凹的阶梯地形
Figure 1. The three types of terrain models (a) The level terrain； (b) The terrain with a simple step； (c) The step terrain with a sharp convex； (d) The step terrain with a sharp concave； (e) The step terrain with a rounded convex; (f) The step terrain with a rounded concave
![]()
图 2 对应图1(a)—(f) 6种地形的地表x分量速度7—9 s快照
Figure 2. Snapshots of x-component velocity waveforms on the surface position corresponding to the six types of terrains in Figs.1(a)-(f) ranging from 7 s to 9 s
![]()
图 3 台阶下测线 蓝色、 绿色、 黄色、 红色、 黑色分别 对应图1中(b)—(f)的地形
Figure 3. The lower lines of steps Blue, green, yellow, red, black lines correspond to the terrains in Figs.1(b)-(f), respectively
![]()
图 4 不同角度台阶下测线 绿色、 红色分别对应图1中(c)、 (d)不同角度的地形
Figure 4. The lower lines of steps with different angles Green and red lines correspond to the terrains with different angles in Figs.1(c) and 1(d), respectively
![]()
图 5 各个模型地表接收到的狓方向速度峰值图 (a)水平地形;(b)夹角为60°的尖凸地形;(c)夹角为90°的尖凸地形;(d)夹角为120°的尖凸地形; (e)简单台阶地形;(f)夹角为120°的尖凹地形;(g)夹角为90°的尖凹地形;(h)夹角为60°的尖凹地形
Figure 5. The x-componet peak velocities observed on the surface of each model (a)Thelevel terrain;(b)The terrain with 60° sharp convex;(c) Theterrain with 90° sharp convex;(d) The terrain with 120° sharpconvex;(e) Simple two-dimensional step terrain;(f) The terrain with 120°sharp concave;(g) The terrain with 90° sharp concave;(h) The terrain with 60° sharp concave
![]()
图 6 台阶端线x分量波形图(左侧图为上测线波形， 右侧图为下测线波形) (a) 简单二维台阶地形波形； (b) 尖凸台阶地形波形； (c) 尖凹台阶地形波形
Figure 6. The x-component velocity waveforms (the left panels are waveforms measured on upper line， and the right ones are measured on lower line) (a) The diagram of the simple two-dimensional step terrain； (b) The diagram of the step terrain with sharp convex； (c) The diagram of the step terrain with the sharp concave
![]()
图 7 震源在上测线(左侧图)和下测线(右侧图)投影点的x分量速度波形图 图(a)， (b)， (c)分别为图6(a), (b), (c)中震源在上下测线投影点的速度波形
Figure 7. The x-component velocity waveformｓ of the projected point of the source on the upper (left panels) and lower (right panels) lines Figs.(a), (b), (c) separately correspond to the velocity waveforms projected on the point from the source to the survey line in Figs.6(a), (b), (c)
![]()
图 8 震源在上测线(左侧图)和下测线(右侧图)投影点的x分量加速度波形图 图(a)， (b)， (c)分别为图6(a)， (b)， (c)中震源在上下测线投影点的加速度波形
Figure 8. The x-component acceleration waveforms of the projected point of the source on the upper (left panels) and lower (right panels) lines Figs.(a), (b), (c) separately correspond to the velocity waveforms projected on the point from the source to the survey line in Figs.6(a), (b), (c)
![]()
图 9 表1和表2中测点位置
Figure 9. Distribution of the measuring points listed in Tables 1 and 2
表 1 三维台阶地形与水平地形速度峰值比较(放大倍数)
Table 1 Comparison of the peak velocities of three-dimensional step terrain with those of the horizontal terrain (magnification)
下载: 导出CSV
表 2 三维台阶地形与水平地形加速度峰值比较(放大倍数)
Table 2 Comparison of the peak accelerations of three-dimensional step terrain with those of the horizontal terrain (magnification)
下载: 导出CSV
-
薄景山, 李秀领, 李山有. 2003. 场地条件对地震动影响研究的若干进展[J]. 世界地震工程, 19(2): 11-15. Bo J S, Li X L, Li S Y. 2003. Some progress of study on the effect of site conditions on ground motion[J]. World Earthquake Engineering, 19(2): 11-15 (in Chinese).
陈丙午. 1982. 不规则地形对地震动及震害的影响[J]. 地震工程与工程振动, 2(1): 12-19. Chen B W. 1982. Effect of irregular topography on earthquake motion and earthquake damage[J]. Earthquake Engineering and Engineering Vibration, 2(1): 12-19 (in Chinese).
董良国. 2005. 复杂地表条件下地震波传播数值模拟[J]. 勘探地球物理进展, 28(3): 187-194. Dong G L. 2005. Numerlcal simulation of seismic wave propagation under complex near surface conditions[J]. Progress in Exploration Geophysics, 28(3): 187-194 (in Chinese).
胡元鑫, 刘新荣, 罗建华, 张梁, 葛华. 2011. 汶川震区地震动三维地形效应的谱元法模拟[J]. 兰州大学学报: 自然科学版, 47(4): 393-402. Hu Y X, Liu X R, Luo J H, Zhang L, Ge H. 2011. Simulation of three-dimensional topographic effects on seismic ground motion in Wenchuan earthquake region based upon the spectral-element method[J]. Journal of Lanzhou University: Natural Sciences, 47(4): 393-402 (in Chinese).
景立平, 卓旭炀, 王祥建. 2005. 复杂场地对地震波传播的影响[J]. 地震工程与工程振动, 25(6): 16-23. Jing L P, Zhuo X Y, Wang X J. 2005. Effect of complex site on seismic wave propagation[J]. Earthquake Engineering and Engineering Vibration, 25(6): 16-23 (in Chinese).
刘晶波. 1996. 局部不规则地形对地震地面运动的影响[J]. 地震学报, 18(2): 239-245. Liu J B.1996. The effect of local irregular topography on seismic ground motion[J]. Acta Seismologica Sinica, 18(2): 239-245.
袁晓铭, 廖振鹏. 1996. 任意圆弧形凸起地形对平面SH波的散射[J]. 地震工程与工程振动, 16(2): 1-12. Yuan X M, Liao Z P. 1996. Scattering of plane SH waves by a cylingrical hill of circular-arc cross-section[J]. Earthquake Engineering and Engineering Vibration, 16(2): 1-12 (in Chinese).
荣棉水, 李小军. 2007. 局部地形对出平面运动谱特性的影响分析[J]. 中国地震, 23(2): 147-156. Rong M S, Li X J. 2007. The effect analysis of topography on the spectrum property of anti-plane movement[J]. Earthquake Research in China, 23(2): 147-156 (in Chinese).
荣棉水, 李小军, 吕悦军, 尤红兵. 2009. 平台地形对地震地面运动特征周期值的影响[J]. 中国地震, 25(2): 178-185. Rong M S, Li X J, Lu Y J, You H B. 2009. Effect of protruding topography on characteristic period of ground motion[J]. Earthquake Research in China, 25(2): 178-185 (in Chinese).
王海云, 谢礼立. 2010. 自贡市西山公园地形对地震动的影响[J]. 地球物理学报, 53(7): 1631-1638. Wang H Y, Xie L L. 2010. Effects of topography on ground motion in the Xishan park, Zigong city[J]. Chinese Journal of Geophysics, 53(7): 1631-1638 (in Chinese).
王伟. 2011. 地震动的山体效应[D]. 哈尔滨: 中国地震局工程力学研究所: 1-173. Wang W. 2011. Effect of Hill Topography on Ground Motion[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 1-173 (in Chinese).
周红. 2007. 两种地震波传播方法的研究[D]. 北京: 北京大学: 1-47. Zhou H. 2007. The Study of Two Kinds of Seismic Wave Propagation Methods[D]. Beijing: Peking University: 1-47 (in Chinese).
周红, 陈晓非. 2007. 凹陷地形对Rayleigh面波传播影响的研究[J]. 地球物理学报, 50(4): 1182-1189. Zhou H, Chen X F. 2007. A study on the effect of depressed topography on Rayleigh surface wave[J]. Chinese Journal of Geophysics, 50(4): 1182-1189 (in Chinese).
周红, 高孟潭, 愈言祥. 2010. SH波地形效应特征的研究[J]. 地球物理学进展, 25(3): 775-782. Zhou H, Gao M T, Yu Y X. 2010. A study of topographical effect on SH waves[J]. Progress in Geophysics, 25(3): 775-782 (in Chinese).
周正华, 张艳梅, 孙平善, 杨柏坡. 2003. 断层对震害影响的研究[J]. 自然灾害学报, 12(4): 20-24. Zhou Z H, Zhang Y M, Sun P S, Yang B P. 2003. Study on effect of fault on seismic damage[J]. Journal of Natural Disasters, 12(4): 20-24 (in Chinese).
Boore D M. 1972. A note on the effect of simple topography on seismic SH waves[J]. Bull Seismol Soc Am, 62(1): 275-284.
Jih R S, Mclaughlin K L, Der Z A. 1988. Free-boundary conditions of arbitrary topography in a two-dimensional explicit elastic finite-difference scheme[J]. Geohphysics, 53(8): 1045-1055.
Komatitsch D, Vilotte J P. 1998. The spectral element method: An efficient tool to simulation the seismic response of 2D and 3D geological structure[J]. Bull Seismol Soc Am, 88(2): 368-392.
Komititsch D, Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation[J]. Geophys J Int, 139(3): 806-822.
Seriani G. 1998. 3-D large-scale wave propagation modeling by spectral element method on Gray T3E multiprocessor[J]. Comp Meth Appl Mech Eng, 164(1): 235-247.
Tessmer E, Kosloff D, Behle A. 1992. Elastic wave-propagation simulation in the presence of surface-topograghy[J]. Geophys J Int, 108(2): 621-632.
Tessmer E, Kosloff D. 1994. 3-D elastic modeling with surface topography by a Chebychev spectral method[J]. Geophysics, 59(3): 464-473.
Wang Y B, Takenaka H, Furumura T. 2001. Modeling seismic wave propagation in a two-dimensional cylindrical whole-earth model using pseudo-spectral method[J]. Geophys J Int, 145(3): 689-708.
-
期刊类型引用(6)
1. 李鸿晶，王竞雄. 时域谱元法的质量特性模型及其构建方法. 地震学报. 2022(01): 60-75 . 
本站查看
2. 冯广军，刘中宪，陈頔，黄磊，李程程，刘国瑞. 近断层山体地形三维地震动放大效应谱元法模拟. 防灾减灾工程学报. 2022(04): 778-787 . 百度学术
3. 巴振宁，赵靖轩，吴孟桃，梁建文，塔拉. 基于逆断层动力学模型的三维山体地震动谱元法模拟. 地震工程与工程振动. 2021(03): 32-42 . 百度学术
4. 张季，梁建文，巴振宁. SH波入射时凸起场地的地形和土层放大效应. 地震工程与工程振动. 2016(02): 56-67 . 百度学术
5. 刘甲美，高孟潭，陈鲲. 地形效应影响下地震动参数与斜坡稳定性的相关性研究. 地震学报. 2015(05): 865-874+886 . 本站查看
6. 赵瑞斌，张建军，刘中宪，马利华. 基于粘弹性人工边界的阶梯地形地震波动问题分析. 世界地震工程. 2015(03): 220-227 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 557
- HTML全文浏览量: 252
- PDF下载量: 22
- 被引次数: 10
