Numerical simulation for the influence of two-end grounded cables on georesistivity observation
-
摘要: 针对我国地震监测预报中地电阻率定点连续观测中存在的偶极接地线的干扰问题, 本文将台站区域地层简化为3层均匀介质模型, 将接地线等效为偶极接地的电阻体, 建立了接地线干扰地电阻率观测的耦合物理模型. 通过有限元分析软件ANSYS模拟分析不同电性断面情况下接地线对地电阻率观测的影响, 同时分析这种干扰的产生机理, 并结合实际观测中存在的干扰问题作了对比验证分析. 结果表明: ① 接地线使得供电电极产生的地下对称性电场分布发生局部调整, 从而影响地电阻率观测; ② 接地线对地电阻率观测的影响主要取决于线缆的位置及方位角的大小; ③ 适当增大电极埋深可以减小其对地电阻率观测的影响; ④ 电性结构的差异性决定干扰变化幅度的大小. 本文结果对相关台站地电阻率观测异常分析落实及干扰源避让和观测系统改造具有参考意义.Abstract: Two-end grounded cables often generate interference to continuous georesistivity observation at fixed sites for earthquake monitoring and prediction in China. By taking the grounded cables as two-end grounded resistors and simplifying the medium of geoelectric observation sites into horizontally inhomogeneous three-layered medium, a coupled physical model is built up in this paper. Based on this model, influences of two-end grounded cables on georesistivity observation are simulated under different electric structures by using the finite element analysis software ANSYS. Furthermore, the effects of interference factors, such as position, azimuth and buried depth of electrodes, on georesistivity observation are analyzed. And the interference mechanisms are also discussed. Besides, some existing interferences are also presented to give out a comparative study. The results showed that the first, the grounded cables can cause local adjustment of the symmetric underground electric field distribution generated by the current electrode, affecting normal georesistivity observation; the second, the effects of grounded cables on georesistivity observation, mainly depend on position of cables and their azimuth; the third, the effects tend to be reduced obviously with buried depth of electrodes increasing; and the forth, the difference of the electric structures determine the magnitude of interference. The simulation results are of significance as a reference to analyzing the similar resistivity anomalies, choosing the evaded distance of the interference source and the reform of the observing system.
-
引言
随着数字地震观测资料应用的日益广泛和深入,地震学者对震相自动识别技术日趋关注,震相自动识别在海量资料分析和实时资料处理等领域得到了较快的发展.
1976年,Stevenson发表了其在地震自动分析方面的研究成果,其方法核心即为长短时平均能量比(short term average/long term average,简写为STA/LTA)(Stevenson,1976). 次年Stewart(1977)提出了用于近震实时检测和定位的方法. 1978年,Allen发表了应用单通道地震记录进行地震自动检测和到时识别的文章(Allen,1978). 1982年,Allen又对当时震相自动识别的应用现状和未来发展进行了总结和展望,同时提出了用特征函数作为输入参数的STA/LTA算法(Allen,1982). 该特征函数思想经过不断发展目前仍在广泛应用(李山有等,2006; 高淑芳等,2008). 迄今,经过30多年的发展,各种新的震相自动识别算法随着数字信号处理技术、 概率论以及自动控制理论的发展被广泛提出和应用. 我们将震相自动识别分为3步. 第一步: 预处理. 是对原始信号进行各种滤波和时频转换,包括傅里叶变换、 Gaber变换、 Wigner-Ville分布、 小波变换、 小波包变换、 Hilbert-Huang变换等预处理算法(刘希强等, 1998,2000,2002; 杨配新等,2004; Granet,1983). 第二步: 震相识别算法. 又可分为能量成分算法(如STA/LTA算法)、 频率成分算法(如瞬时频率算法)、 波形算法(如AIC算法)、 波动矢量差异算法(如偏斜角)和动态特征算法(如偏振分析、 线性度、 功率谱和频谱)等5部分(Roberts et al,1989). 第三步: 方法综合判定. 对第二步的算法进行各种组合和阈值设定,并依据各种情形确定相应的识别程序及方法,包括后期的用人工神经网络对判定方法进行训练(Baer,Kradolfer,1987). 经过上述3步的震相自动识别方法在P波s震相识别方面得到了广泛的应用,并取得了良好的效果. 但是在S波自动识别方面,由于P波尾波以及各种反射震相,如PmP的强干扰,STA/LTA算法用于S波震相自动识别的效果较差,Roberts等(1989)基于S波与P波质点振动方向的差异,提出了用偏振分析方法识别S波. Cichowicz(1993)提出了采用偏斜角、 偏振度和切向能量与总能量比值3种参数相乘得到的值作为判断依据的方法,该方法总有效性达到65%—70%. Bai和Kennett(2000)采用能量分析、 自回归表征和瞬时频率技术并与偏振分析结合进行综合震相识别,此方法对震中距17.3°—41.6°的各种远震震相的识别能力较高,包括远震S波震相识别,但用于近震识别S波震相识别精度较低. Diehl等(2009)提出了用于地震层析成像的S波自动识别方法,该方法需经过STA/LTA判定、 偏振分析、 坐标系变换、 自回归Akaike信息准则(auto regressive-Akaike information criterion,简写为AR-AIC)等一系列综合判定,计算量较大,可用于资料的后续分析. 经过对2500个S波震相识别结果与人工分析结果比较,该方法最大误差大约为0.27 s. Amoroso(2012)对台网资料后续分析的S波自动识别采用了偏振滤波与波形一致性方法. Kuperkoch等(2012)采用波形自回归预测方法,对地方震、 近震和远震的S波进行了自动判定,识别的平均误差为0.5 s±0.8 s.
本文旨在研究根据实时地震波形进行地震早期预警方面的快速S波震相识别. 依据马强(2008)的地震预警动态定位的6种情形,S波到时圆包含地震预警动态定位的重要信息,对S波进行识别是地震预警动态定位的必要环节. 本文尝试性地提出一种S波自动识别的方法,秉承“滤波越少,算法越好”(“the less filtering,the better the algorithm”)的思想(Douglas,1997),对原始三分向记录波形不做任何滤波处理,由于已知由其它自动识别方法得到的P波到时,从而对S波到时可进行快速自动高精度的识别. 对于P波的精确识别,推荐采用刘希强等(2009)的三阶统计Akaike信息准则(three order cumulative-Akaike information criterion,简写为TOC-AIC)方法.
1. 识别方法
本文方法的基本思路是根据由其它方法自动识别的P波的动态特征,求得波形的波动矢量,即P波的质点振动方向,并选取计算窗长对后续波形进行质点振动方向滑动计算,求得后续波形质点振动方向与P波质点振动方向的夹角,即偏斜角; 将偏斜角和水平能量占总能量的比值的平方积作为确定识别区间的依据; 然后根据方差Akaike信息准则(variance-Akaike information criterion,简写为VAR-AIC)判定两个水平分向S波初动位置,并对两个水平分向各自的识别结果进行分析判断,确定S波震相到时.
1.1 确定窗长
鉴于震中距小于100 km 的地方震,其P波的周期约为0.05—0.2 s,S波的周期约为0.1—0.5 s(朱元清等,2002). 根据山东省地震台网密度,以及Nyquist采样定理,选取P波到时之后0.5 s的波形数据,计算P波的卓越频率(Boore,1983; Andrews,1986)

式中,fP为P波卓越频率,m1和m2计算公式为

式中,v2(f)和D2(f)分别为速度功率谱密度和相应的位移功率谱密度. 将fP/2作为S波的卓越频率,计算窗长

式中,fS为采样率,lw为计算波形偏振方向的窗长.
鉴于本研究所用资料为山东数字地震台网记录的数据,为速度记录,所以在计算m2之前要将速度记录仿真为位移记录. 本文采用的数值积分方法为Newton-Cotes求积算法

式中,[a,b]为积分区间,C(n)k为Cotes系数.

从计算精度和计算量两方面综合分析,本文选择n=4时的Newton-Cotes公式

该计算结果具有5次代数精度,其截断误差为

同时,对窗长进行限定,大于采样率的1/5,小于采样率的一半(即Nyquist频率).
1.2 计算偏斜角
选取P波之后lw长度的数据计算其最大特征值对应的特征向量,即P波的偏振方向(质点振动方向),单台三分向lw长度的数据协方差矩阵为

长度为lw的任意两组变量x和y的协方差为

从lw长度之后开始进行逐点滑动,求得各个数据窗最大特征值对应的特征向量,并计算与P波偏振方向的夹角.
1.3 水平能量与总能量比值
水平能量与总能量比值,即窗内两个水平分向能量和与三分向能量和的比值,计算公式为

式中,x和y为两个水平分向波形数据序列,z为垂直分向波形数据序列.
1.4 VAR-AIC
Maeda(1985)提出了直接根据地震图记录而得到AIC函数的方法,称为VAR-AIC方法. AIC函数的最小值对应的时间就是地震震相初至. AIC函数表示为

式中,var(x[1,k])和(var(x[k+1,N])分别表示两个时间段内数据的方差.
1.5 判定标准
对于S波的初步判定,选取偏斜角和水平能量与总能量比值的平方积作为特征函数(cf),即

阈值选择自P波开始至计算点位置的均值的5倍加方差的5倍. 以此特征函数作为判定S波识别区间的判据,对S波进行初步判定. 之后选取初判位置前3个lw长度和后3个lw长度的数据作为精确判定的区间,采用VAR-AIC方法分别对NS和EW分向进行S波的精确识别. 对于识别的两个分向各自的S波位置,如果时间差小于0.1 s,则认为二者的差值是由于S波分裂造成,则取二者的平均值作为识别的S波位置; 如果二者的差值大于0.1 s,则认为某一个分向存在误识别,分别计算两个分向各自的识别位置前后lw长度信号的信噪比,取信噪比较大的一个分向的判定结果作为S波的识别位置.
2. 资料和结果分析
结合山东数字地震台网记录的数据,将本文震相识别方法的结果与人机交互处理结果进行对比,最后确定其有效性.
按照震级不同选取29个地震事件,每个地震事件选择震中距100 km范围内的台站记录,要求记录可以精确识别P波到时,共选取56个台站的118个三分向记录. 通过这118个三分向记录波形对本文方法进行了测试. 本研究所涉及的地震及台站分布见图 1. 本文所选取的地震事件参数见表 1. 地震选取考虑以下3方面: ① 信噪比随震级的变化; ② 信噪比随震中距变化; ③ 信噪比受台站背景噪声及地震射线传播路径影响. 此方法统筹同一台站对不同震级地震的识别能力,又兼顾全省台站各自背景噪声的不同,从而在全省不同位置选取地震事件,同时也在相近震中位置选取不同震级的事件(烟台莱州震群和濮阳范县附近4次不同震级地震).
表 1 本文所选取的地震事件参数Table 1. Detailed information of selected earthquake events
为了体现该方法的实时性,在对三分向记录进行S波识别时,采用与现有Jopens系统类似的方法,将三分向数据以数据包形式分割发送,每秒1个包,模拟从数采实时获取数据.
图 2为118个三分向记录的自动识别结果与人机交互识别结果的对比,即以人机交互结果为标准,自动识别结果的误差分布图. 图中横轴为二者的差值,纵轴为S波对P波尾波的信噪比. 对118个三分向记录的识别结果按照S波对P波尾波的信噪比不同进行了统计(表 2). 对于误差大于0.1 s的震相识别作为无效识别. 本文所采用的118个三分向记录,其信噪比均小于12. 最高信噪比为11.56,最低信噪比为-2.28.
表 2 识别结果统计Table 2. Statistics on identification results
如表 2所示,本文所提出的S波实时自动识别方法对于信噪比大于5的地震事件,按照识别误差小于0.1 s的精度要求,识别有效率高达89.39%,有效识别平均误差为0.05 s. 对于低信噪比大于0小于5的三分向地震记录,按照识别误差小于0.1 s的精度要求,识别有效率达到65.79%,有效识别平均误差为0.07 s. 综上,本文识别方法在信噪比相对较低的情况下能够实现较高的有效率和较小的识别误差.
3. 讨论与结论
本文提出了一种用于地震早期预警的S波震相实时自动识别方法. 该方法不对原始信号进行任何滤波处理,直接根据偏斜角和水平能量与总能量比值确定识别区间; 采用VAR-AIC方法对两个水平分向分别进行精确识别; 对两个识别结果进行判断,确定S波初动时刻.
经过对118个三分向记录的实际应用验证,本文方法具有识别有效率高、 识别误差小的优点. 由于P波尾波以及各种反射震相的强干扰,S波的信噪比整体偏低,不利于S波有效识别及识别精度的提高. 本文方法对于信噪比大于5的地震记录可以实现S波震相高精度的实时有效识别. 虽然与目前已有的P波0.02 s的识别精度还有一定差距,但0.1 s的识别误差小于Amoroso等(2012)和Kuperkoch等(2012)的识别误差,而且本方法识别有效率高达89.39%.
本文方法是在基于P波已经由其它方法精确识别的基础上提出的. 其P波卓越频率、 窗长及P波偏振方向的计算均受P波的识别精度影响,但是鉴于目前P波识别精度已达到0.02 s,而且本文选择窗长为0.5 s,故本方法能够达到较高的识别精度.
-
图 2 水平3层介质中对称四极装置(剖面)(a)和偶极接地线模型示意图(俯视)(b)图(b)中左上角(b1)小图为其右下角(b2)小图中接地线PQ的细节结构示意图
Figure 2. (a)Schlumberger array of apparent resistivity observation in horizontally inhomogeneous three-layered medium;(b)The physical model of two-end grounded cable. And the part(b1)in the upper-left corner is the details of grounded cable PQ shown in part(b2)in the lower-right corner
表 1 模型的电性结构参数
Table 1 Physical parameters of the electric structures for the three-layered model

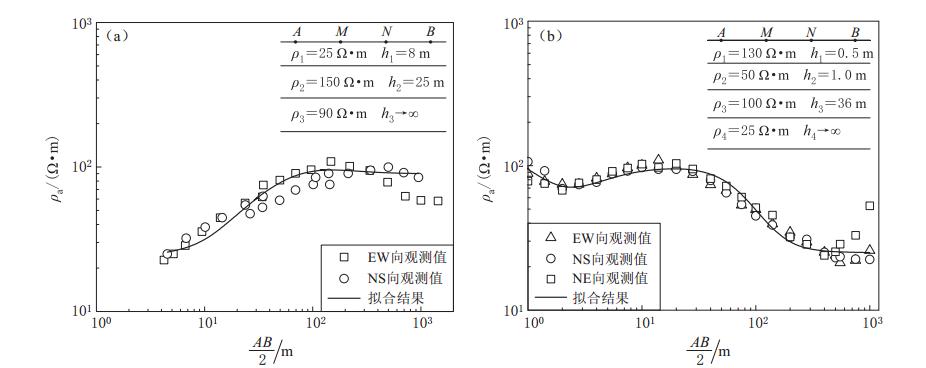
表 2 新沂台和固原台偶极接地线干扰地电阻率观测的模拟结果与实测结果对比
Table 2 Comparison of the simulated and observed georesistivities at the stations Xinyi and Guyuan under the influence of two-end grounded cables

-
-
期刊类型引用(5)
1. 孔凌浩,严鹏,刘晓,周朝,张翔宇,卢文波. 爆破地震波中P波及S波初至自动识别方法. 振动与冲击. 2025(05): 253-262 .  百度学术
百度学术
2. 杨招伟,卢文波,高启栋,陈明,胡浩然,严鹏,王高辉. 爆破地震波中S波识别方法及其应用. 爆炸与冲击. 2018(01): 28-36 .  百度学术
百度学术
3. 田优平,赵爱华. 基于小波包和峰度赤池信息量准则的P波震相自动识别方法. 地震学报. 2016(01): 71-85+157 .  本站查看
本站查看
4. 张楚旋,李夕兵,董陇军,马举,陈光辉. 三函数四指标矿震信号S波到时拾取方法及应用. 岩石力学与工程学报. 2015(08): 1650-1659 .  百度学术
百度学术
5. 刘希强,蔡寅,赵瑞,曲保安,赵银刚,冯志军,李红. 区域地震信号自动识别方法及应用(英文). Applied Geophysics. 2014(02): 128-138+252 .  百度学术
百度学术
其他类型引用(3)





 下载:
下载: