A method for computing the aperiodicity parameter of the strong earthquake recurrence interval
-
摘要: 确定强震复发间隔变异系数在强震发生概率的计算中具有重要意义. 考虑到由小样本量地震序列计算得到变异系数的估计值与实际值可能存在一定的偏差， 本文提出了一种计算强震复发间隔变异系数的新方法. 该方法首先利用最大似然估计法计算出大量小样本地震序列的变异系数估计值； 然后先对这些变异系数的估计值进行标准化处理， 再对这些标准化的变异系数估计值进行统计分析； 最后在广泛搜集的39个地震序列的基础上， 利用该方法计算得到一个通用的变异系数值(α=0.34)， 并讨论了该值的物理意义及其应用.Abstract: Determining the aperiodicity parameter α (equivalent to the familiar coefficient of variation) is important for calculating the possibility of large earthquake occurrence. Considering the deviation between the estimate values of α from small sample of earthquake sequences and the actual values of α， this paper presents a new method for computing α. Firstly, a large number of estimated values of α for small samples from earthquake sequences are calculated by maximum likelihood estimate method， and then the estimated values are standardized and statistically analyzed. Finally, based on the 39 recurrent earthquake sequences, a general value of α is given (α=0.34), and the physical meaning and application of the value are also discussed.
-
Keywords:
- strong earthquake /
- recurrence interval /
- aperiodicity parameter /
- normalization
-
-
![]()
图 1 抽取5次(a)和7次(b)地震事件的变异系数α ′ 值分布
Figure 1. Distribution of aperiodicity parameter α ′ values for 5-event (a) and 7-event (b) synthetic earthquake series
![]()
图 2 抽取5次地震事件α ′ 值的正态概率检验(a)和对数正态概率检验(b)
Figure 2. The normal probability test (a) and log-normal probability test (b) of α ′ values for 5-event synthetic earthquake series
![]()
图 4 本文所统计的39个地震序列变异系数α ′ 估计值的分布柱状图
Figure 4. The histogram of estimated aperiodicity parameter α ′ for 39 earthquake sequences in this study
表 1 不同地震事件数目和α值所对应的a值
Table 1 a values corresponding to different event number of synthetic earthquake series and α values
序列的地震数目 α=0.4 α=0.5 α=0.6 a ρ a ρ a ρ 5 0.3478 0.8695 0.4219 0.8438 0.4885 0.8142 6 0.3566 0.8915 0.4346 0.8692 0.5064 0.8440 7 0.3632 0.9080 0.4437 0.8874 0.5186 0.8643 8 0.3679 0.9197 0.4504 0.9008 0.5267 0.8778 9 0.3717 0.9292 0.4561 0.9122 0.5332 0.8887 10 0.3742 0.9355 0.4592 0.9184 0.5395 0.8992 11 0.3770 0.9425 0.4632 0.9264 0.5437 0.9062 
下载: 导出CSV
表 2 39个地震序列及其α ′ 的估计值
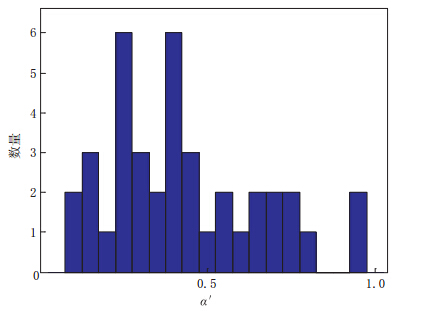
Table 2 Estimated α ′ values for 39 earthquake sequences
地震地点 M 最近一次地 震发生年份 地震 数目 中值 α′ 参考文献 Copper River Delta，USA 9.2 1964 9 683 0.23 Plafker和Rubin(1994) Willipa Bay，USA 9.0 1700 7 526 0.53 Atwater和Hemphill-Haley(1997) Wairarapa fault，NZ 8.2 1855 5 1551 0.18 Van Dissen和Berryman(1996) Nankaido，Japan 8.1 1946 9 158 0.40 Ishibashi和Satake(1998) Tonankai，Japan 8.1 1944 7 210 0.75 Ishibashi和Satake(1998) Pallett Creek，USA 7.8 1857 10 146 0.97 Sieh等(1989) Wrightwood，USA 7.8 1857 6 150 0.71 Biasi和Weldon(1998) Pitman Canyon，USA 7.8 1812 6 180 0.96 Seitz等(1997) Miyagi-Oki，Japan 7.5 1978 11 36 0.27 Utsu(1984) Brigham City，USA 7.0 BC130 6 1 476 0.31 McCalpin和Nishenko(1996) Tanna fault，Japan 7.0 1930 7 972 0.65 The Tanna Fault Trenching Research Group (1983) Concepcion Chile 8.3 1939 5 92.3 0.10 Nishenko和Buland(1987) Middleton Island 1964 6 1020.8 0.16 Nishenko和Buland(1987) Irpinia fault，Italy 6.9 1980 5 2058 0.58 Pantosti等(1993) 延矾盆地北缘断裂南段 1338 7 5412 0.34 刘静和汪良谋(1996) 怀涿盆地北缘断裂南段 6 5120 0.36 刘静和汪良谋(1996) 华山山前断裂段 8.0 1556 5 1766 0.24 刘静和汪良谋(1996) 古浪断裂天桥沟段 8.0 1927 7 4602 0.42 李正芳等(2012) 古浪断裂黄羊川段 8.0 1927 5 1795 0.39 郑文俊等(2004) 老虎山—毛毛山断裂老虎山段 7.0 1888 6 1130 0.27 郑文俊等(2004) 老虎山—毛毛山断裂毛毛山段 5 1713 0.12 郑文俊等(2004) 海原断裂带西段 7.7 1920 8 1943 0.38 郑文俊等(2004) 海原断裂带中段 7.5 1920 7 1083 0.54 张培震等(2003) 冷龙岭断裂西段 5 1364 0.26 李正芳等(2012) 鄂拉山断裂 5 2475 0.44 李正芳等(2012) 东昆仑断裂带库赛湖段 8.1 2001 6 3522 0.15 李正芳等(2012) 东昆仑断裂带玛沁段 6 1724 0.70 李正芳等(2012) 东昆仑断裂带玛曲段 7 1964 0.76 李正芳等(2012) 昌马—俄博断裂昌马断层段 7.6 1932 7 1860 0.48 李正芳等(2012) 黄河—灵武断裂灵武段 5 5250 0.42 李正芳等(2012) 新疆富蕴断裂 8.0 1931 8 1204 0.31 时振梁等(1997) 贺兰山东麓断裂 8.0 1739 5 1995 0.31 闵伟等(2000) 大青山山前断裂土右旗西段 5 2260 0.63 冉永康等(2003) 大青山山前断裂呼和浩特段 7 2462 0.15 冉永康等(2003) 色尔腾山山前断裂 8 814 0.44 陈立春(2002) 乌拉山山前断裂 6 1346 0.44 陈立春(2002) 延庆盆地北缘断裂韩方段 5 4846 0.24 陈立春(2002) 灵武断裂 5 5288 0.42 柴炽章等(2001) 六盘山东麓断裂 6 6250 0.80 向宏发等(1999)
下载: 导出CSV
表 3 迭代过程
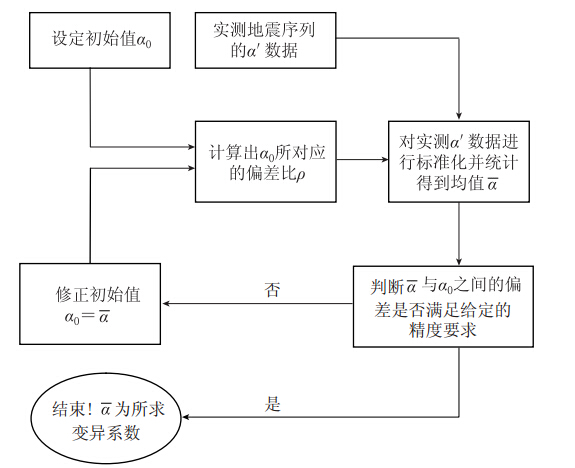
Table 3 The iterative process
α ρ(5) ρ(6) ρ(7) ρ(8) ρ(9) ρ(10) ρ(11) a α0=0.4000 0.8695 0.8915 0.9080 0.9197 0.9292 0.9355 0.9425 0.3434 α1=0.3434 0.8812 0.9060 0.9192 0.9300 0.9380 0.9442 0.9497 0.3395 α2=0.3395 0.8830 0.9041 0.9211 0.9313 0.9384 0.9448 0.9507 0.3393 α3=0.34
下载: 导出CSV
-
陈立春. 2002. 河套断陷带的古地震、 强震复发规律和未来可能强震地点[D]. 北京: 中国地震局地质研究所: 16-48. Chen L C. 2002. Paleoearthquakes,the Law of Strong Earthquake Recurrence and Potential Sites for the Occurrence of Future Strong Earthquakes in the Hetao Fault-Depression Zone[D]. Beijing: Institute of Geology,China Earthquake Administration: 16-48 (in Chinese).
Atwater B F,Hemphill-Haley E. 1997. Recurrence Intervals for Great Earthquakes of the Past 3500 Years at Northeastern Willapa Bay[R]. Washington: U S Geological Survey Professional Paper 1576: 108.
Biasi G,Weldon R J. 1998. Paleoseismic date refinement and implications for seismic hazard estimation[M]//Dating and Earthquakes: Review of Quaternary Geochronology and Its Application to Paleoseismology. U S Nuclear Regulatory Commission,NURGE-5562: 3-61-3-66.
Ellsworth W L,Matthews M V,Nadeau R M,Nishenko S P,Reasenberg P A,Simpson R W. 1999. A Physically Based Earthquake Recurrence Model for Estimation of Long-Term Earthquake Probabilities[R]. U S Geological Survey Open-File Report: 99-522.
Ishibashi K,Satake K. 1998. Problems on forecasting great earthquakes in the subduction zones around Japan by means of paleoseismology[J]. J Seismol Soc Japan, 50 (Suppl): 1-21.
Plafker G,Rubin M. 1994. Paleoseismic Evidence for “Yo-Yo” Tectonics Above the Eastern Aleutian Subduction Zone: Coseismic Uplift Alternating with Even Larger Interseismic Submergence: Proceedings of the Workshop on Paleoseismology[R]. U S Geological Survey Open-File Report 94-568: 155-157.
Reid H F. 1910. The Mechanics of the Earthquake,the California Earthquake of April 18,1906[R]. Washinton: State Investigation Commission,Carnegie Institution of Washington,(2): 43-47.
Working Group on California Earthquake Probabilities. 2003. Earthquake Probabilities in the San Francisco Bay Region: 2002 to 2031[R]. U S Geological Survey Open-File Report: 03-214.
Working Group on California Earthquake Probabilities. 2007. The Uniform California Earthquake Rupture Forecast,Version 2[R]. U S Geological Survey Open-File Report: 2007-1437.
计量
- 文章访问数: 839
- HTML全文浏览量: 325
- PDF下载量: 10
