Response of the non-homogeneous saturated foundation to incident plane P-SV waves
-
摘要: 基于Biot多孔介质波动模型,研究了非均匀饱和土层对平面P-SV波入射时的动力响应.考虑饱和土地基的物理力学特性沿厚度方向连续变化,利用亥姆霍兹矢量分解原理和动力刚度法,分析了平面入射P-SV波在非均匀饱和土层中的反射和透射,并给出了基岩表面和自由表面处反射系数和透射系数的计算表达式.基于理论推导结果,数值分析了平面SV波入射下非均匀饱和土自由场地的动力响应,其中假设饱和土地基的物理力学性质沿土层深度按幂律梯度变化.数值结果表明,平面SV波入射所引起的地面位移与基岩位移之比均随土层厚度和土体的非均匀程度、波的入射角和入射频率的增加而减小,且其竖向位移比的减小更为显著,厚土层对地震波的耗散作用尤为明显.Abstract: Based on Biot's model for saturated porous media,the dynamic responses of non-homogeneous saturated soil was studied by using Helmholtz vector decomposition principle and exact dynamic stiffness method (EDSM) when P-SV wave was incident from bedrock.Reflection and transmission of incident plane P-SV wave in non-homogeneous saturated soil were analyzed considering the continuous variation of physical and mechanical properties about saturated foundation along the thickness direction.As a consequence,the general calculation formulas about the reflection coefficient and transmission coefficient of bedrock and free-field on the both surfaces were given.As numerical examples,assuming that the material properties of the saturated foundation had an exponential law distribution and gradient variation along the thickness-coordinate,the dynamic response of non-homogeneous saturated soil and free-field to incident plane SV was discussed.The numerical results indicate that the ratio of ground displacement to bedrock displacement decreases with the increase of the thickness and heterogeneity index of saturated soil,incident angle and frequency of seismic wave.The vertical displacement ratio decreases more significantly than the horizontal one.The dissipation of seismic wave caused by the thickness of soil layer is obvious,which all should be taken into account in engineering practice especially on complex layered situations.
-
引言
自Biot(1956a,b)建立了液饱和多孔介质的本构方程以来,地震波在非均匀饱和土中的传播问题,已经在地震工程、岩土工程等多个领域得到了广泛关注.国内外众多研究者为饱和土波动理论的完善和发展起到了重要的推动作用(陈龙珠等,1987; Corapcioglu,1991;王立忠,吴世明,1995;杨峻等,1996).吴世明(1997)以弹性波基本理论为基础,作了较为系统的理论研究,对深入研究土的动力特征具有重要的学术价值;门福录(1981)引入准微观连续条件的概念,得到了液饱和多孔介质的动力学方程组;陈少林和廖振鹏(2002,2003)将透射公式推广到考虑衰减波入射时的情形,分析了衰减波入射时两种极限情形下反射系数的变化情况. Deresiewicz和Rice(1964)研究了地震波在液饱和土体界面处的反射和透射问题; Stoll和Kan(1991)求解了地震波在海洋沉积土界面处的反透射问题,丰富了海洋领域的地震勘探资料; Santos等(1992)导出了弹性波在液体与多孔介质交界面上位移和能量的透射和反射系数,分析了黏滞修正系数的影响作用.乔文孝等(1992)、杨峻和吴世明(1997)分析了波以任意角度由一种液饱和土层入射到另一种液饱和土层时的反射和透射的结果;胡亚元等(1998)、赵成刚等(1999)和叶陈江等(2005)讨论了弹性波在弹性土与饱和土分界面的反射和透射问题.以往的研究多集中在单相介质(Wolf,1985)和均匀饱和多孔介质方面.而弹性波在非均匀饱和多孔介质分层界面上的动力问题是波动理论的一个研究热点,在实际工程中有着非常广泛的应用,但目前研究较少.鉴于此,本文将分析地震波从基岩处以任意角度入射,向上传播到非均匀饱和土中,并在土层中反射和透射时所引起土体的动力特性.
动力刚度法的概念是由Kolousek(1973)提出的,多用于解决工程中的结构振动问题,最早用于考察杆、梁及框架结构的动力响应(Kolousek,1973).动力刚度法也称为精确方法,只要建立了最初的位移场假设,就可以精确地求解运动微分方程,且不需要再引入其它任何假设或近似.张引科等(2000)用传递矩阵法处理了弹性饱和多孔介质半空间的动力问题,分析指出传递矩阵法将边界上的应力和位移与介质内的应力和位移联系在一起,以方便数值模拟.钟阳等(1995,2003)、钟阳和赵晓雷(2005)分别用传递矩阵法和刚度矩阵法对弹性半空间的动力响应问题作了分析,研究表明刚度矩阵法可以克服传递矩阵法在数值计算中的缺陷,使计算更为精确.
本文将在Biot多孔介质理论的基础上,假设饱和土地基的物理力学性质沿土层深度按幂律梯度变化,分析当平面P-SV波从基岩入射时上覆非均匀饱和土地基的动力响应问题.理论推导出SV波在非均匀饱和土中反射和透射时所引起非均匀饱和土上表面与基岩上表面位移比的计算表达式.通过给出具有实际意义的数值算例,探讨地震波的入射角和入射频率对动力响应的影响,并分析非均匀饱和土的土层厚度和土体的非均匀性对地震波引起的位移比的影响.
1. 基本方程
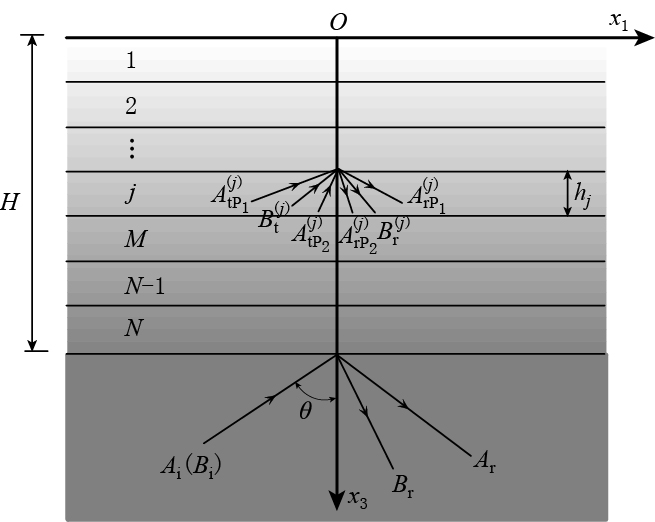
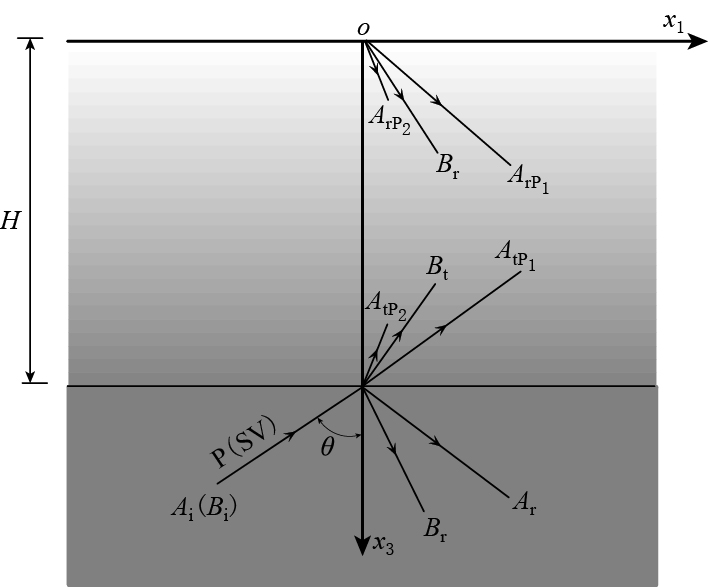
图 1为考虑饱和土的自由场地示意图.位于基岩上的饱和土覆盖层厚度为H,从基岩入射的平面P波或SV波的入射角为θ,波幅为Ai或Bi.
1.1 两相多孔介质的控制方程及通解
根据Biot多孔介质理论,均匀、各向同性的饱和土介质弹性波动方程为(Zhou et al,2013)


式中: u和w分别为固体骨架位移矢量和流体相对于土骨架的位移矢量; e=ui,i,ζ=-wi,i; λ和μ为固体骨架拉梅弹性常数; b=η/kf,η为流体黏滞系数,kf为渗透系数; α和M为考虑两相材料压缩性的Biot参数,α=1-K/Ks,1/M=(α-n)/Ks+n/Kf,其中K,Ks和Kf分别为固体骨架、固体颗粒和孔隙流体的体积模量; m=ρf/n为与孔隙水的质量密度及孔隙几何特征有关的参数; ρ=(1-n)ρs+nρf为混合物介质的质量密度,其中n为孔隙率,ρs和ρf分别为固相和液相的密度.
根据亥姆霍兹矢量分解原理,位移矢量 u和w可以用势函数φu,ψu和φw,ψw表示为

假设饱和土层中位移势函数为

式中: AtP1和ArP1分别为透射P1波和反射P1波的波幅系数; AtP2和ArP2分别为透射P2波和反射P2波的波幅系数; Bt和Br分别为透射SV波和反射SV波的波幅系数; k1=ωsinθ/v,表示平面波在x1方向的波数,ω=2πf为圆频率,f为地震波的入射频率; v为平面波的传播速度.其中
由于这里只考虑x1ox3平面内的P-SV波,与x2坐标无关,故可得饱和土的位移与应力为

式中,
ξ1=-2μk3S2-γ12(λ+α2M+αMδP1),ξ2=-2μk3P22-γ22(λ+α2M+αMδP2).
1.2 单相固体介质的控制方程及通解
将基岩视为单相固体弹性介质,类似于对饱和土的推导过程.假设位移势函数为

式中:φb和ψb分别为基岩中波的标量势函数和矢量势函数; Ai和Ar分别为入射P波和反射P波的波幅系数; Bi和Br分别为入射SV波和反射SV波的波幅系数; k3bP=ωcosθ/vP,vP为入射P波的波速;k3bS=ωcosθ/vS,vS为入射SV波的波速.
基岩的位移与应力分别为

式中,ub为基岩的位移矢量.
2. 饱和土自由场地响应
土层在沉积过程中,由于受不同的环境、地理和气候等条件的影响,导致土体特性沿土层深度表现出明显的差别.而对于层厚较大的同一类土,这一沿着地层深度的非均匀特性尤为突出.介质材料的非均匀特性,导致以此介质材料为研究对象的问题的控制方程变得比较复杂,通常情况下采用变系数的偏微分方程组,很难获得相应的解析解答.因此,在土体的厚度方向上,将非均匀饱和土层简化为许多均匀的饱和土薄层,如图 2所示.所简化的土层层数N的多少根据问题的精度要求来决定.图中给出了第j层中P1波、 P2波和SV波的反射和透射.
2.1 传递矩阵
令P=k3P1x3,Q=k3P2x3,R=k3Sx3,将式(5)整理得到:

式中,上标j表示第j层的饱和土.其中,
显然,式(8)对于第j层中介于0—hj的任何深度都成立.此外,如果取x3=0,则可得第j层顶面上的位移分量.由于分界面处存在位移与应力的连续性条件,则第j层顶面上的位移分量等于第j-1层底面的对应量.用下标B表示底面,T表示顶面.当x3=0时,P=0,Q=0,R=0,容易得出此时的F(j)矩阵,记为F0(j).其逆矩阵记为f0(j),即第j-1层底面上的位移与应力分量值可表示为

式(9)左右两边同时左乘f0(j),代入式(8)中,可建立起第j-1层底面与第j层的位移分量之间的关系,即

矩阵F(j)和f0(j)中各元素均为地震波在第j层介质传播时的纵波速度、横波速度、土层厚度和入射角的函数,代表了波在该层介质中传播时的物理特征.令G(j)= F (j) f0 (j),则矩阵G(j)可称为第j层的层矩阵.当x3=hj时,则有 Ghj (j)= Fhj (j) f 0(j),结合式(10)有

根据第N-1层底面与第N层顶面的位移与应力分别相等的边界条件,递推得到第N层介质顶面附近的位移和应力与第一层底面的位移和应力之间的关系为

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
将第一层层底与层顶的位移与应力的关系式,结合第N层层顶的位移与应力的关系式带入式(12)中可得

令a = F 0(N) Y,b = MF h1(1) Y,Y为构造矩阵,
则式(13)可简化为

其中,
X 1=[ ArP1(1) AtP1(1) ArP2(1) AtP2(1) Br(1) Bt(1) ]T,XN=[ ArP1(N)AtP1(N)ArP2(N)AtP2(N) Br(N)Bt(N) ]T.
2.2 边界面条件
在自由表面处,σ33=σ13=p=0,即

在第N层土与基岩交界面处,ub1=u1,ub3=u3,σb33=σ33,σb13=σ13,w3=0,即

结合式(14)、(15)和(16)建立线性方程组:

式中,
C=[cij]14×14,D=[dij]14×1,
X=[ArP1(1) AtP1(1) ArP2(1) AtP2(1) Br(1) Bt(1) ArP1(N) AtP1(N) ArP2(N) AtP2(N) Br(N) Bt(N) Ar Br]T.
求解式(17),可获得第一层、第N层和基岩中的未知波幅系数.将所求的波幅系数带入式(5)和式(7)中,取x3=0,即可求得饱和土体上表面与基岩顶面的位移比值.由于文中无法得到解析解,只能求得数值解,故在以下算例中均采用Matlab编程进行数值计算.
3. 数值算例分析
3.1 非均匀饱和土材料性质
假设饱和土层的孔隙率沿厚度方向按幂函数形式连续变化(Zhou et al,2013),即

式中: γ表示梯度因子,不同的γ值代表非均匀程度不同的多孔介质; H为上覆非均匀饱和土的厚度.算例中取上表面处(x3=0)的孔隙率为n(0)=n0=0.45,仿照Wang等(2013)取值方法,其它物理力学参数取值分别为λ0=4.43×107 N/m2,μ0=2.70×107 N/m2,α=1,ρ0=2 100 kg/m3,M0=4.967×109 N/m2,ρνf0=1 000 kg/m3,kf0=6×10-4 cm/s,n0=0.45.下表面处(x3=H)的孔隙率为n(H)=0.25.
此外假设饱和土的物理力学性质与孔隙率n的关系(Zhou et al,2013)为

式中: κ为土体物理力学性质随孔隙率变化的指数; G为饱和土体的ρ,λ,μ,α和M等物理力学参数; n0,kf0和G0为饱和土体上表面处孔隙率以及相应的物理力学参数值.选取基岩的材料参数分别为λb=2.059×109 N/m2,μb=1.427×109 N/m2,ρb=2 460 kg/m3.
3.2 方法的有效性
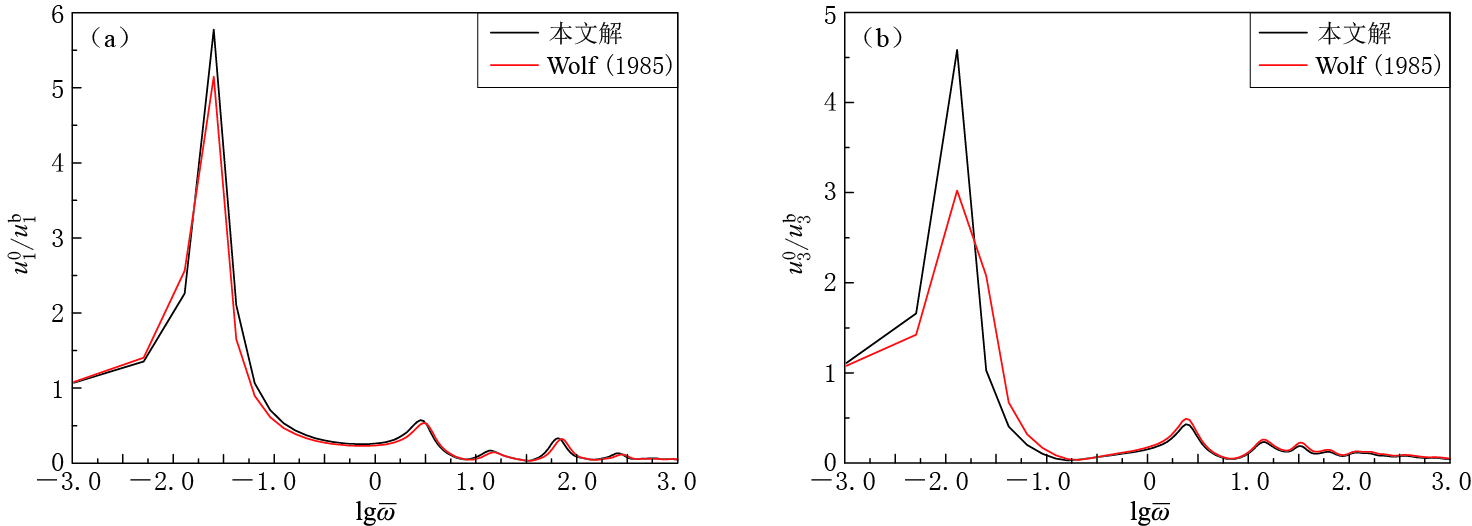
取非均匀参数γ=0,将非均匀地基退化为单层均质地基.考虑SV波水平入射的情形,与Wolf(1985)中具有相同求解条件的单相介质的解答进行比较,如图 3所示.可以看出,两者结果基本一致.
3.3 数值模拟结果
本文中仅考虑平面SV波入射的情形,即入射P波的波幅Ai=0.选取参数γ=1,κ=1,H=20 m.通过试算,选取分层数N=100可满足精度要求.
This page contains the following errors:
error on line 1 at column 68: Extra content at the end of the documentBelow is a rendering of the page up to the first error.
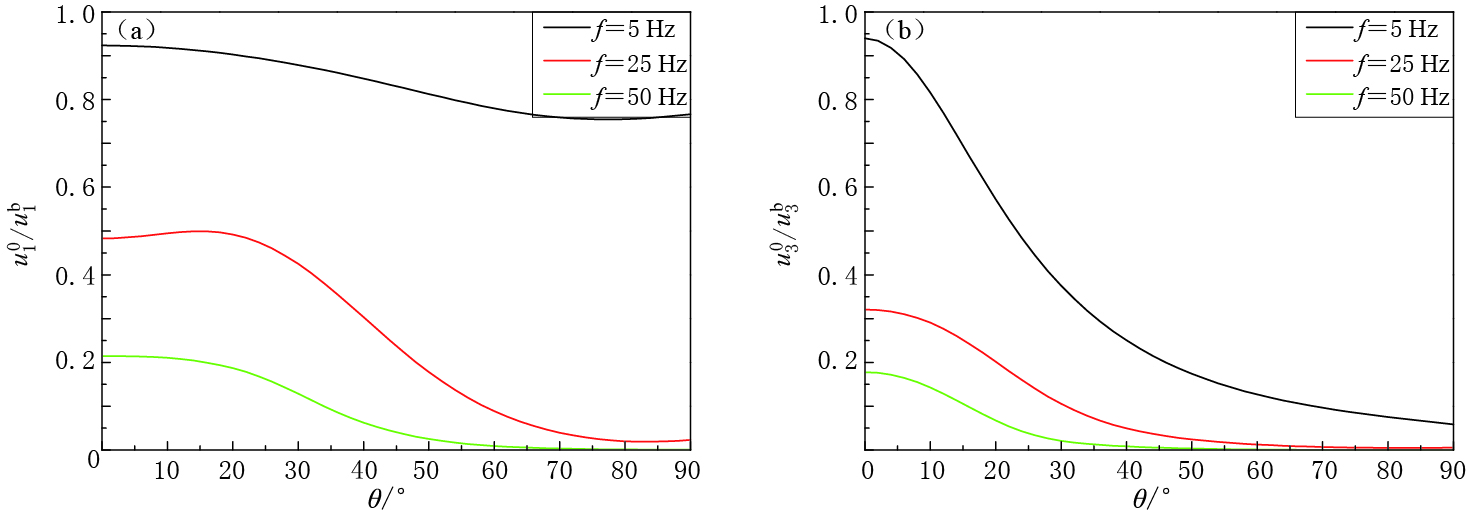
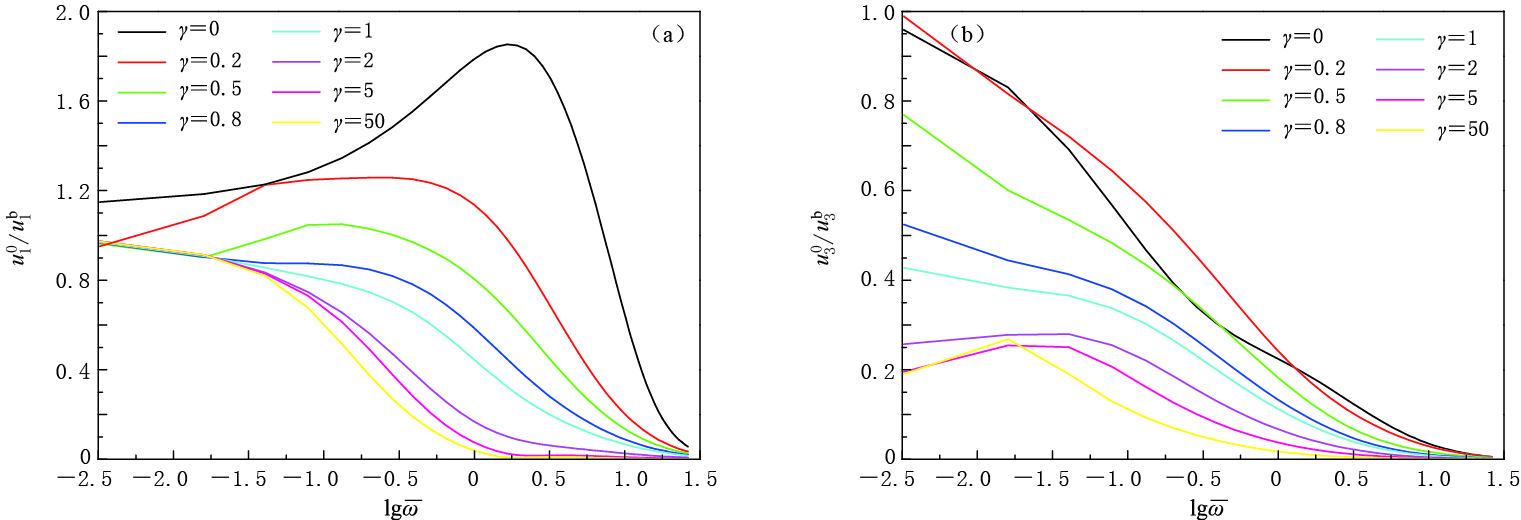
图 4为了分析土体非均匀性对自由场地动力响应的影响,图 7给出了不同非均匀指数情形下,位移比与频率的变化曲线.可以看出,位移比随频率的增加大体呈减小趋势,与图 4中所得结论一致.随着非均匀指数的增大,竖向位移比和水平向位移比的最大值将减小.
4. 讨论与结论
基于Biot多孔介质模型,应用动力刚度法研究了平面P-SV波入射时所引起的非均匀饱和土自由场地的响应,数值分析了SV波入射时,位移比与频率、入射角、上覆非均匀饱和土层厚度以及非均匀指数之间的关系,结果表明:
1)动力刚度法对于求解非均匀饱和土中地震波的传播具有很好的适用性,其求解简单方便、易于理解、便于编程,并且具有较高的求解精度.
2)平面P-SV波的入射角、频率以及土体的非均匀性对饱和土层的动力响应有很大的影响,与均质土地基相比具有明显不同的特性.
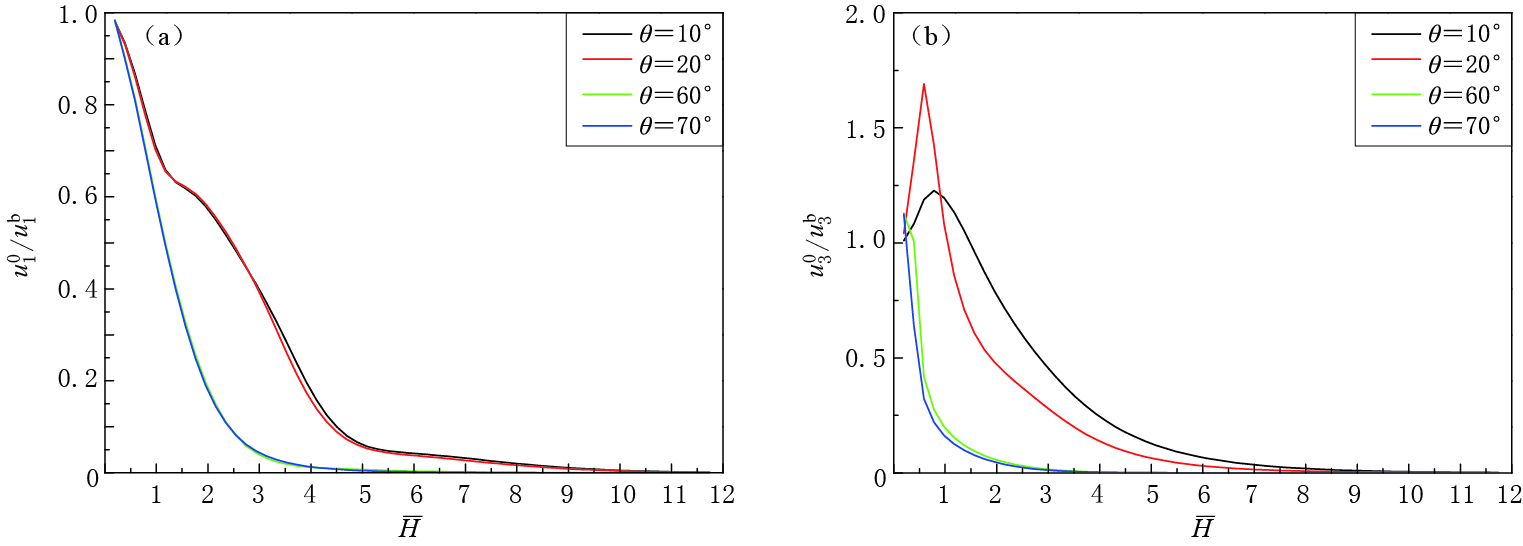
3)随着土层厚度的增加,地面的动力响应逐渐减小并趋于零,表明厚土层对地震波的耗散作用尤为明显;地面位移与基岩位移之比均随饱和土的非均匀指数、地震波的入射角和入射频率的增加而减小,且竖向位移比减小得更为显著.
本文考虑土体在沉积过程中自身的非均匀性,基于混合物连续介质的基本理论,针对具有梯度饱和土覆盖层的空间体中地震波的传播特性进行系统分析,对非均匀材料力学和混合物连续介质理论的发展有促进作用.鉴于实际饱和土层比较复杂的特点,本文根据求解需求及梯度饱和土覆盖层的特性,只假设了饱和土介质的物理力学参数沿深度呈幂律梯度变化的情况,以往也有假设为指数变化和线性变化的情况.更精确的土介质参数与深度的函数关系应根据多组试验进行拟合确定,这将是下一步研究的重点.
-
-
吴世明.1997.土介质中的波[M].北京:科学出版社:14-26. Wu S M.1997.Wave Propagation in Soils[M].Beijing:Science Press:14-26(in Chinese).
Biot M A.1956a.Theory of propagation of elastic waves in a fluid-saturated porous solid:Ⅰ.Low-frequency range[J].J Acoust Soc Am,28(2):168-178.
Biot M A.1956b.Theory of propagation of elastic waves in a fluid-saturated porous solid:Ⅱ.Higher frequency range[J].J Acoust Soc Am,28(2):179-191.
Corapcioglu M Y.1991.Wave propagation in porous media:A review[G]//Transport Processes in Porous Media NATO ASI Series 202.Netherlands:Springer:373-469.
Kolousek V.1973.Dynamics in Engineering Structures[M].London:Butterworths:20-50.
Wolf J P.1985.Dynamic Soil-Structure Interaction[M].New Jersey:American Society of Civil Engineers:112-131
-
期刊类型引用(5)
1. 焦豪,马强,周凤玺. P波入射下饱和冻土自由场地地震地面运动分析. 冰川冻土. 2024(01): 137-151 .  百度学术
百度学术
2. 周凤玺,姚桃岐,柳鸿博. P_1波在非饱和土自由边界上反射的能量特性研究. 振动工程学报. 2024(12): 2066-2077 .  百度学术
百度学术
3. 柯小飞,陈少林,张洪翔. 海水-海床体系在P-SV波入射时的动力响应分析. 建筑结构. 2018(S2): 915-919 .  百度学术
百度学术
4. 赵宇昕,陈少林. 关于传递矩阵法分析饱和成层介质响应问题的讨论. 力学学报. 2016(05): 1145-1158 .  百度学术
百度学术
5. 赵瑞斌,毕铭,张彦,刘中宪,吴朝阳. 半空间SV波斜入射在土体中的应力路径及空心圆柱动扭剪试验模拟. 世界地震工程. 2016(04): 231-238 .  百度学术
百度学术
其他类型引用(11)




 下载:
下载: