Equivalent anisotropic first-order pseudo-acoustic wave equations modeling and its efficiency analysis
-
摘要: 为克服各向异性弹性波动方程正演模拟的局限,本文研究了各向异性介质拟声波方程的交错网格有限差分数值解法.首先,从VTI介质胡克定律和qP-qSV波频散关系两种思路出发,通过声假设近似,给出了两种不同形式的VTI介质一阶拟声波方程,并通过引入波场的伪速度分量,推导了一种新的VTI介质一阶应力-速度方程,并通过旋转坐标系将其推广到TTI介质中;其次,构造了一阶拟声波方程的交错网格高阶有限差分格式,并推导了相应的PML边界条件;最后,对本文方法中固有的qSV人为干扰波的产生机制和压制方法进行了简单讨论.数值结果表明:3种一阶拟声波方程在运动学和动力学上是等价的,相对于各向异性弹性波正演模拟,其节省了内存,提高了计算效率;各向异性因素会影响反射波旅行时和振幅等波场特征,在后续的处理、反演和解释中不可忽略;VTI介质HESS模型的逆时偏移结果也验证了本文方法的合理性.Abstract: In order to overcome the limitations of anisotropic elastic wave equations modeling, this paper studied anisotropic pseudo-acoustic wave modeling by using staggered-grid finite-difference method. Starting from two different ideas, i.e., Hooke’s law and qP-qSV dispersion relation for VTI media, two first-order pseudo-acoustic wave equations in two forms for VTI media are given. Meanwhile, a new VTI first-order stress-velocity equations is derived through introducing the pseudo-velocity components of the wavefields, and then they are generalized to TTI media through the rotated coordinate system. Then the staggered-gird high-order finite-difference forms of the first-order pseudo-acoustic wave equations and the corresponding PML boundary condition are deduced. Finally, the inherent qSV-wave artifact generating mechanism and suppression method are discussed briefly. Numerical results show that the three first-order pseudo-acoustic wave equations are equivalent in kinematics and dynamics. Compared with anisotropic elastic wave modeling, they can save computational memory and enhance the efficiency. Anisotropic factor can affect the travel-time and amplitude of the reflection wave so we cannot ignore them in subsequent processing,inversion and interpretation. The reverse-time migration results of VTI-HESS model also validate the method proposed in this paper.
-
引言
正演模拟是研究地震波在地球介质中传播规律的重要工具.目前波动方程类的数值模拟方法主要有有限差分法、虚谱法和有限元法等(董渊等,2003).有限差分法(裴正林,2004)的主要优点是计算速度快,占用内存小;缺点是会产生数值频散,而且传统的规则网格有限差分法精度较低.交错网格有限差分法(Virieux,1986;董良国等,2000)则可以大大减少数值频散、提高计算精度,是实际应用中常用的一种数值模拟方法.
地球介质中广泛存在着各向异性,横向各向同性(transversely isotropic media,简写为TI)介质是最普遍的一种,包括VTI(vertical transversely isotropic media),HTI(horizon taltransversely isotropic media)和TTI(tilted transversely isotropic media)介质.基于各向同性假设的正演模拟方法不足以准确地描述实际地球介质中地震波的传播.在以往的研究中,考虑各向异性的弹性波动方程正演模拟取得了一定的进展(裴正林,2004).该方法是用三分量矢量场来描述弹性波波场,其正演结果能够获得比标量波场更丰富的波场信息.但其存在一定的缺陷(何兵寿,张会星,2006):①各向异性参数复杂,物理意义不明确,在实际生产中难以获得;②多分量数据占用资源大,计算效率低;③由于多分量地震勘探成本高,目前野外采集仍然以纵波地震资料为主,多分量弹性波理论的应用受到资料不足的限制.
为克服各向异性弹性波动方程在实际应用中的局限,Alkhalifah(2000)从VTI介质的精确qP-qSV波频散关系出发,假设垂向剪切波速度vS0=0,推导了VTI介质四阶拟声波方程.为降低四阶偏微分方程计算的复杂性,Zhou等(2006)和Du等(2008)从声学近似的频散关系出发,通过引入不同的辅助波场函数,分别推导了两种VTI介质二阶耦合拟声波方程.为结合交错网格技术实现精确的有限差分数值模拟,Hestholm(2009)推导了一阶偏微分形式的VTI介质拟声波方程.Duveneck等(2008)从声学近似的胡克定律出发,也推导了二阶形式和一阶应力-速度形式的VTI介质拟声波方程.与Alkhalifah(2000)方程一样,几种拟声波方程均存在低速度、低振幅的qSV人为干扰波问题(Grechka et al,2004),而这种干扰波的存在会影响正演模拟和偏移成像的最终结果.
本文以VTI介质为例,首先从声学近似的胡克定律和频散关系两个不同角度出发,研究了3种不同形式的VTI介质一阶拟声波方程,并引入旋转坐标系,将其推广到TTI介质中;然后采用交错网格有限差分方法求解其关于时间和空间的一阶偏微分算子,实现了各向异性拟声波数值模拟,并通过数值结果的对比分析验证了3种一阶拟声波方程在运动学和动力学上的等价性;最后应用VTI介质拟声波逆时偏移算法实现了各向异性HESS模型的准确成像.
1. 各向异性介质一阶拟声波方程推导
1.1 从声学近似的胡克定律角度
首先对VTI介质胡克定律进行经典的声假设近似(Alkhalifah,2000).令垂向剪切波速度vS0=0,得到用Thomsen参数表示的VTI介质声假设近似胡克定律:

式中:σij和εkl分别为应力张量和应变张量(下标1,2,3分别对应x,y,z方向);ρ为密度;vP0为垂向纵波速度;ε和δ为Thomsen各向异性参数(Thomsen,1986).
波动方程1.式(1)两端对时间t求导,并结合运动方程ρ∂vi/∂t=∂σij/∂xj(下标ij=1,2,3分别对应x,y,z方向),可得到一阶应力-速度形式的VTI介质拟声波方程(Duvenecket al,2008):

式中:u,v,w分别为沿x,y,z方向的速度分量;p=σ11=σ22和q=σ33分别为水平应力分量和垂直应力分量;vPx为对称平面内的qP波速度,v2Px=v2P0(1+2ε);vPn为qP波的正常时差速度,v2Pn=v2P0(1+2δ).
1.2 从声学近似的qP-qSV波频散关系角度
从声假设近似的三维VTI介质频散关系出发,

式中:w为角频率;kx,ky,kz为空间波数;vP0,vPx,vPn的物理意义同式(2).由于式(3)中相应的时空域四阶偏微分方程中存在四阶空间和时空混合偏导,不易直接求解,Alkhalifah(2000)引入辅助中间变量p(x,y,z,t),令p=∂F2/∂t2,将其转换为二阶偏微分形式的波动方程:

基于同样的声近似频散关系,Du等(2008)引入新的辅助波场,得到二阶耦合形式的VTI介质拟声波方程:

式中,p=p(x,y,z,t)为伪应力波场,q=q(x,y,z,t)是为简化计算而引入的辅助波场.
波动方程2.Hestholm(2009)在式(4)的基础上,通过引入3个中间变量κ,ψ,ζ,得到一阶偏微分形式的VTI介质拟声波方程:

式中:u,v,w分别为x,y,z方向上的质点振动速度;η=(ε-δ)/(1+2δ)为非椭圆参数.
波动方程3.本文在式(5)的基础上,引入波场p和q的伪速度分量up,vp,wp和uq,vq,wq,并分别沿x,y,z3个方向进行分解,得到新的VTI介质一阶应力-速度拟声波方程:

式中,up,vp,wp和uq,vq,wq分别表示波场p和q在x,y,z方向的伪速度分量.
1.3 从VTI介质推广至TTI介质
由VTI介质推广至TTI介质只是增加了代数复杂性,两者在物理意义上并没有本质的差异.因此,可以通过引入对称轴倾角θ和方位角φ,将垂直坐标系X(x,y,z)旋转至倾斜坐标系X′(x′,y′,z′)中.引入三维坐标系的旋转关系(Cheng,Kang,2014):

式中,旋转矩阵A依赖于倾角θ和方位角φ,即

由此可得旋转坐标系与垂直坐标系下的一阶偏导算子关系为

式中AT为旋转矩阵A的转置.将VTI介质一阶拟声波方程中相应的偏导算子通过坐标旋转后即可得到TTI介质形式.
2. VTI介质一阶拟声波方程的数值解法
2.1 交错网格高阶有限差分格式的构造
交错网格技术的基本思想是计算两个相邻网格点之间的偏导数(董良国等,2000).本文以式(7)的二维形式为例,利用交错网格对其应力和速度分量进行差分离散(图 1),得到时间二阶和空间高阶的交错网格有限差分格式(式(2)和式(6)的差分格式同理可得):

式中:Δt为时间步长;Δx和Δz分别为x和z方向上的空间步长;i,j为空间离散点号;k为时间离散点号;pk+1/2i,j表示(k+1/2)时刻的pi,j值;2N为差分方程的精度;C(N)n为交错网格一阶差分系数.
2.2 完全匹配层边界条件
完全匹配层(perfectlymatchedlayer,简写为PML)边界条件是Berenger(1994)提出的一种高效吸收边界条件,被认为是目前吸收效果最好的边界条件而得到广泛应用.本文以式(7)的二维形式为例,依据PML方程分裂思路,推导相应的时间域PML控制方程如下:

式中:d(x),d(z)为x和z方向的阻尼因子;px,pz和qx,qz分别为波场p,q在x和z方向上的分裂算子.
3. qSV人为干扰波噪音及压制方法
通过数值求解各向异性介质拟声波方程,可以比较准确地描述各向异性介质中qP波的运动学特征.然而在qP波传播的同时,其内部还存在一种菱形状的qSV人为干扰波(Grechkaet al,2004).它的存在不仅会产生噪声问题,而且由于其速度值相对较低,往往还会引起较为严重的数值频散,进而影响正演模拟结果和降低偏移成像精度,因此必须对其进行压制或消除.
3.1 人为干扰波的产生机制
为求解各向异性介质拟声波方程,利用平面波解F(x,z,t)=A(t)exp[i(kxx+kzz)]作为试验解,将其代入式(4)的二维形式可得到两组复数解:

其中

分析可知,该两组复数解按指数增加或衰减的关键取决于指数项的符号.Alkhalifah(2000)研究发现,在实际介质中a1恒为负数,此时式(13)中F1的解对应qP波,其描述的是qP波的传播.当a2为正值,即η=(ε-δ)/(1+2δ)<0时,式(13)中F2的解呈指数增长,这会导致数值结果不稳定.而当a2为负值,即η> 0时,F2对应的解会产生一组“人造的”地震波,其波速小于qP波,实际介质中这种人为干扰波并不存在.其产生的根源是基于声近似的拟声波方程并不是纯qP波方程,虽然将沿对称轴方向的剪切波相速度设为零,但在其它传播方向上的值并不为零,更为重要的是qSV波的群速度值也是非零的.
3.2 人为干扰波的压制方法
由人为干扰波的产生机制可知,当η=0(即ε=δ)时,式(4)退化为各向同性介质纵波方程,此时式(13)中F2的解变为一个与时间无关的函数,即其对应的qSV波不会在各向同性或椭圆各向异性(ε=δ)介质中传播.因此,在激发震源的周围设置一个环状的各向同性或椭圆各向异性盒子,即震源环(Duvenecket al,2008),则可以有效地压制人为干扰波的传播.此外,也可以采用投影滤波方法来进一步压制人为干扰波(Zhang,Zhang,2009).Xu和Zhou(2014)通过引入一个辅助标量算子S,提出一种纯的拟声波方程,以更好地解决复杂各向异性介质中产生的qSV人为干扰波问题.
4. 模型试算
4.1 各向异性均匀介质模型
采用空间十阶和时间二阶的交错网格有限差分方法对3种一阶拟声波方程式(2)、(6)、(7)进行数值模拟.均匀VTI介质模型参数为vP0=3000m/s,ε=0.24,δ=0.10,ρ=1g/cm3.网格大小为301×301,网格尺寸为Δx=Δz=10m,时间采样间隔Δt=1ms,雷克子波震源主频为30Hz,位于模型中心处.
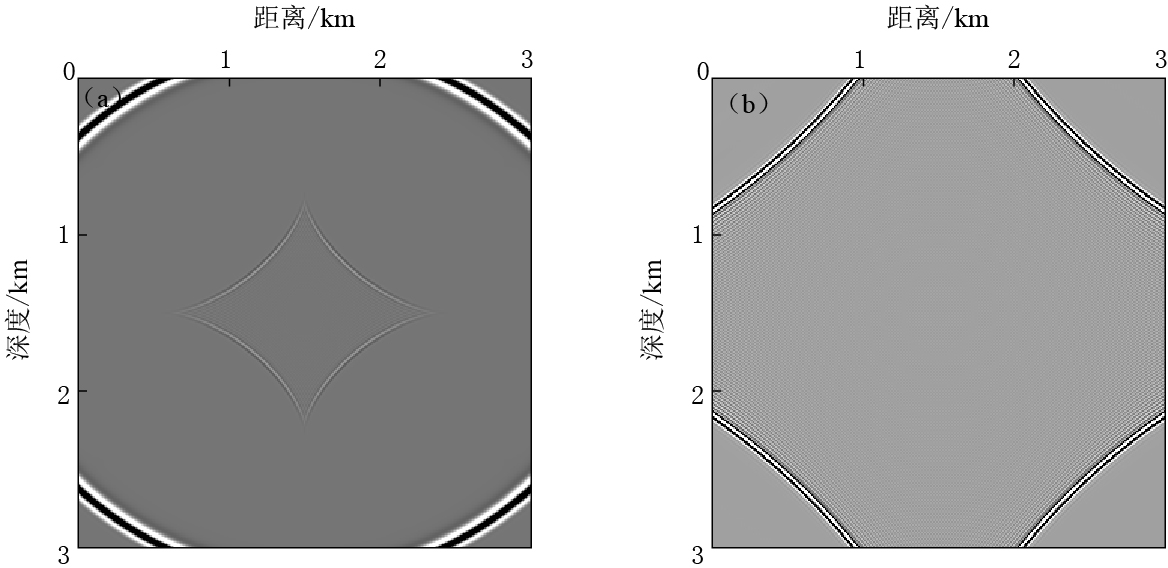
图 2为VTI介质弹性波方程与3种一阶拟声波方程正演模拟得到的波场快照结果.由图 2b,c,d可知,外层传播较快的波是本文主要研究的qP波,且3种拟声波方程正演模拟均存在qSV人为干扰波(内层传播较慢的菱形状波形).与图 2a对比可知,3种一阶拟声波方程均能有效地描述VTI介质中qP波的运动学特征,因此三者在运动学上是等价的.需注意,本文后面给出的各种波动方程的波场快照和地震记录均表示与图 2相同的分量.
![]() 图 2 波场快照对比(t=400 ms)(a)VTI介质弹性波方程正演得到的垂直应力分量波场;(b)用式(2)正演得到的波场q;(c)用式(6)正演得到的波场p;(d)用式(7)正演得到的波场pFigure 2. Comparison of wavefield snapshots (t=400 ms)(a)Wavefield of vertical stress component modeled by elastic wave equation in VTI media;(b)Wavefield q modeled by equation(2);(c)Wavefield p modeled by equation(6);(d) Wavefield p modeled by equation(7)
图 2 波场快照对比(t=400 ms)(a)VTI介质弹性波方程正演得到的垂直应力分量波场;(b)用式(2)正演得到的波场q;(c)用式(6)正演得到的波场p;(d)用式(7)正演得到的波场pFigure 2. Comparison of wavefield snapshots (t=400 ms)(a)Wavefield of vertical stress component modeled by elastic wave equation in VTI media;(b)Wavefield q modeled by equation(2);(c)Wavefield p modeled by equation(6);(d) Wavefield p modeled by equation(7)图 3为应用公式(12)中的PML边界条件对qP波(图 3a)和qSV波(图 3b)的吸收效果.可以看出,PML边界条件不仅可以有效地衰减qP波,对qSV波也有较好的吸收效果,并未因为低速度的人为干扰波而在模型边界处引起较大的数值频散.
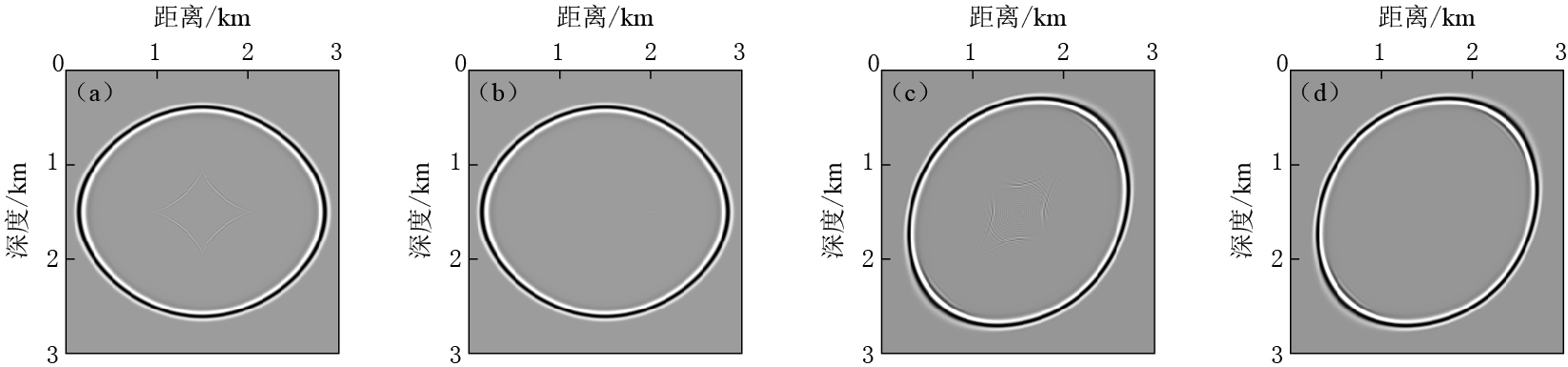
图 4a,b给出了设置震源环前后式(7)所对应的正演模拟结果.在震源附近设置半径为30m的小区域震源环,可以有效地压制拟声波正演模拟中产生的qSV人为干扰波.同时,利用旋转坐标系,可以得到TTI拟声波正演模拟对应的波场快照(图 4c,d).
![]() 图 4 设置震源环前后各向异性介质拟声波正演的波场快照对比(t=400 ms)(a)VTI介质(设置震源环前);(b)VTI介质(设置震源环后);(c)TTI介质(设置震源环前,θ=45°);(d)TTI介质(设置震源环后,θ=45°)Figure 4. Wavefield snapshots comparison of anisotropic pseudo-acoustic wave modeling without and with source box (t=400 ms)(a)VTI media (without source box);(b)VTI media (with source box);(c)TTI media (without source box, θ=45°);(d)TTI media (with source box, θ=45°)
图 4 设置震源环前后各向异性介质拟声波正演的波场快照对比(t=400 ms)(a)VTI介质(设置震源环前);(b)VTI介质(设置震源环后);(c)TTI介质(设置震源环前,θ=45°);(d)TTI介质(设置震源环后,θ=45°)Figure 4. Wavefield snapshots comparison of anisotropic pseudo-acoustic wave modeling without and with source box (t=400 ms)(a)VTI media (without source box);(b)VTI media (with source box);(c)TTI media (without source box, θ=45°);(d)TTI media (with source box, θ=45°)4.2 TTI介质层状模型
4.2.1 波场特征分析
图 5给出了TTI介质层状模型及其各向异性参数.采用3种一阶拟声波方程进行正演模拟,其观测系统如下:模型网格大小为301×151,网格间距为10m×10m;选用震源主频为30Hz的雷克子波,并将炮点置于模型中(1500m,10m)位置处;采用中间放炮、两边接收的方式,共301道,道间距为10m;时间采样间隔Δt=1ms,记录时间为1.5s.
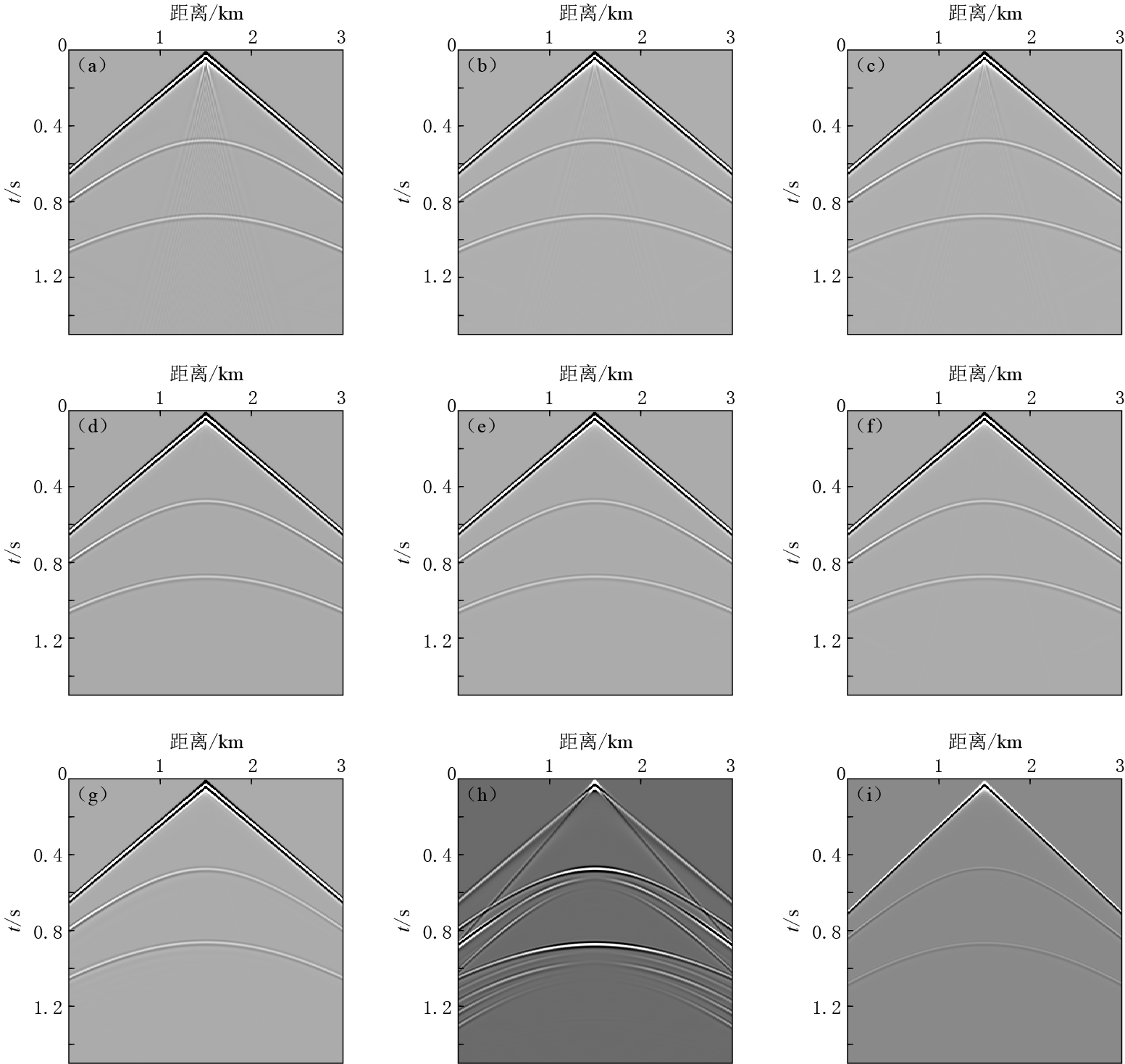
图 6分别显示了3种VTI一阶拟声波方法(图 6a-f)、TTI一阶拟声波方法(图 6g)、VTI弹性波方法(图 6h)和各向同性声波方法(图 6i)正演模拟得到的合成地震记录.从图 6a,b,c中地面位置为1200m处抽取一个近偏移距地震道记录,得到如图 7a所示的单道地震信号对比图.同样,从图 6d,e,f中相应位置处抽取一个地震道,得到的结果如图 7b所示.需注意,图 7中所有的单道地震信号对比图均是切除直达波后的结果,其振幅值表示相对大小,并且只取400—1200ms的旅行时范围,主要研究两个反射层位的有效信号.
![]() 图 6 单炮地震记录对比(a,d)用式(2)正演得到的炮记录;(b,e)用式(6)正演得到的炮记录;(c,f)用式(7)正演得到的炮记录;(g)TTI介质拟声波方程正演得到的炮记录;(h)VTI介质弹性波方程正演得到的炮记录;(i)各向同性声波方程正演得到的炮记录.其中,(a)-(c)为设置震源环前的结果;(d)-(f)为设置震源环后的结果Figure 6. Comparison of single shot seismic records(a,d) Shot records modeled by equation (2);(b,e) Shot records modeled by equation (6);(c,f) Shot records modeled by equation (7);(g) Shot records modeled by TTI pseudo-acoustic wave equation;(h)Shot records modeled by VTI elastic wave equation;(i) Shot records modeled by isotropic acoustic wave equation. Figs.(a)-(c) are results without source box, and Figs.(d)-(f) are results with source box
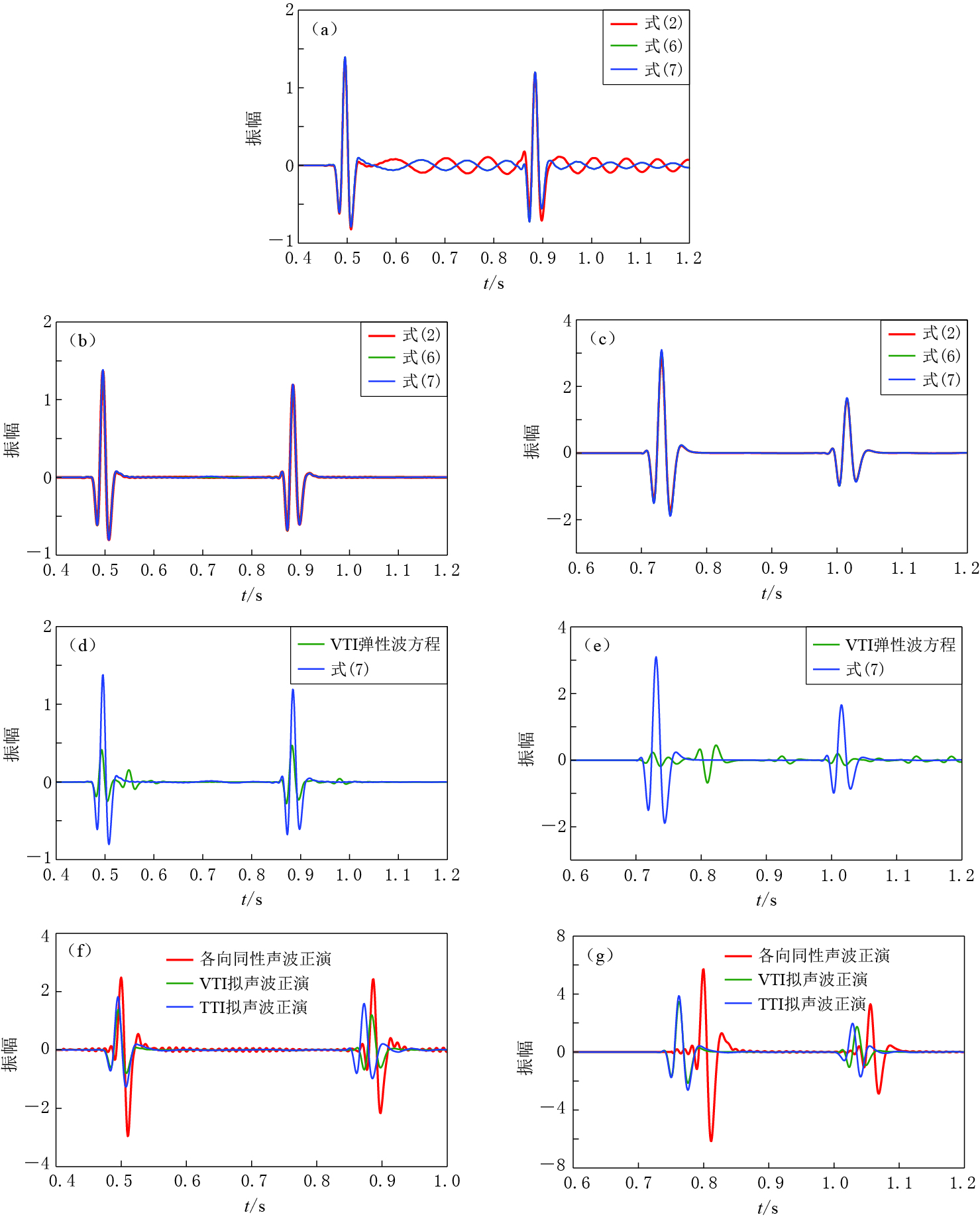
图 6 单炮地震记录对比(a,d)用式(2)正演得到的炮记录;(b,e)用式(6)正演得到的炮记录;(c,f)用式(7)正演得到的炮记录;(g)TTI介质拟声波方程正演得到的炮记录;(h)VTI介质弹性波方程正演得到的炮记录;(i)各向同性声波方程正演得到的炮记录.其中,(a)-(c)为设置震源环前的结果;(d)-(f)为设置震源环后的结果Figure 6. Comparison of single shot seismic records(a,d) Shot records modeled by equation (2);(b,e) Shot records modeled by equation (6);(c,f) Shot records modeled by equation (7);(g) Shot records modeled by TTI pseudo-acoustic wave equation;(h)Shot records modeled by VTI elastic wave equation;(i) Shot records modeled by isotropic acoustic wave equation. Figs.(a)-(c) are results without source box, and Figs.(d)-(f) are results with source box![]() 图 7 单道地震信号对比(a)从图6a,b,c中近偏移距(地面位置为1 200 m)处抽取的单道信号对比;(b,c)从图6d e,f中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比;(d,e)从图6f,h中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比;(f,g) 从图6f,g,i中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比Figure 7. Comparison of single trace seismic signalsFig.(a) is single trace signals comparison of near offset (distance=1 200 m) extracted from Figs.6a,b,c; Fig.(b) and (c) are single trace signals comparison of near offset (distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6d,e,f; Figs.(d) and (e) are single trace signals comparison between near offset (distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6f, h; Figs.(f) and (g) are single trace signals comparison between near offset(distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6f, g, i
图 7 单道地震信号对比(a)从图6a,b,c中近偏移距(地面位置为1 200 m)处抽取的单道信号对比;(b,c)从图6d e,f中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比;(d,e)从图6f,h中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比;(f,g) 从图6f,g,i中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比Figure 7. Comparison of single trace seismic signalsFig.(a) is single trace signals comparison of near offset (distance=1 200 m) extracted from Figs.6a,b,c; Fig.(b) and (c) are single trace signals comparison of near offset (distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6d,e,f; Figs.(d) and (e) are single trace signals comparison between near offset (distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6f, h; Figs.(f) and (g) are single trace signals comparison between near offset(distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6f, g, i图 7a中由于低速度的qSV人为干扰波造成了数值频散,设置震源环后,人为干扰波得到了很好地压制,且几乎不会对qP波产生影响,如图 7b所示.由图 7b还可以看出,3种一阶拟声波正演模拟方法具有很好的一致性,各层同相轴、旅行时和振幅均吻合较好,三者在运动学和动力学上是等价的.类似地,图 7c是从图 6d,e,f中远偏移距(地面位置为200m)处抽取的单道信号对比结果,也能得到相同的结论.
图 7d是从图 6f,h中近偏移距(地面位置为1200m)处抽取的单道地震记录.对比图 7d中蓝线与绿线可知,在两个反射层上,VTI介质一阶拟声波方程与弹性波方程的qP波反射旅行时吻合较好,但振幅值有所差异.因此,本文推导的一阶拟声波方程能够比较准确地模拟VTI介质中qP波的运动学(旅行时和速度等)特征,而在动力学(振幅等)特征上也是VTI弹性波方程的有效近似.类似地,图 7e中远偏移距(地面位置为200m)处抽取的地震道信号对比结果也能得到相同的结论.
图 7f,g分别是从图 6f,g,i中近偏移距(地面位置为1200m)和远偏移距(地面位置为200m)处抽取的单道地震记录.通过对比可知,由于考虑各向异性介质(VTI和TTI)的影响,各层的反射旅行时和振幅均会发生变化,且往往造成旅行时和振幅减小,特别是远偏移距(地面位置为200m)处,这种影响更明显.同时可以看出,模型第二层中受到TTI介质的倾角影响后,振幅和旅行时会进一步发生改变.因此,在实际应用中,对大倾角构造进行处理时必须要考虑到TI介质的倾角因素.
4.2.2 计算效率分析
在波动方程类的正演模拟和逆时偏移中,数值计算效率也是值得关注的.本文将3种VTI一阶拟声波方程、各向同性声波方程及VTI弹性波方程的计算效率进行了对比,其中偏微分算子的有限差分实现占据了波动方程类数值模拟的主要计算量.表 1展示了二维情形下几种波动方程各自的计算量,以及对于同一层状模型(图 5)正演模拟所需的平均计算时间(取10次结果的平均).虽然计算机硬件不同可能会导致计算时间的差异,但是在同等条件下得到的计算时间还是具有一定的参考价值.可以看出:VTI一阶拟声波方程(2)的计算时间最少,与各向同性声波方程相当;而另外两种VTI一阶拟声波方程(6)和(7)的计算时间相对多一些,但仍然少于VTI弹性波方程的计算时间.因此,利用VTI介质拟声波方程不仅能减少计算所需的内存,还能有效地提高计算效率.
表 1 几种波动方程的计算效率对比Table 1. Computational efficiency comparison of the several wave equations方程类型 计算量 平均计算时间/s VTI一阶拟声波方程(2) ∂p/∂x,∂q/∂z,∂u/∂x,∂w/∂z 72 VTI一阶拟声波方程(6) ∂p/∂x,∂p/∂z,∂u/∂x,∂k/∂z,∂w/∂z,∂ζ/∂z 105 VTI一阶拟声波方程(7) ∂p/∂x,∂p/∂z,∂q/∂x,∂q/∂z,∂up/∂x,∂wq/∂z 103 各向同性声波方程 ∂p/∂x,∂p/∂z,∂u/∂x,∂w/∂z 70 VTI弹性波方程 ∂τxx/∂x,∂τxz/∂z,∂τxz/∂x,∂τzz/∂z,∂vx/∂x,∂vx/∂z,
∂vz/∂x,∂vz/∂z130 4.3 VTI介质HESS模型
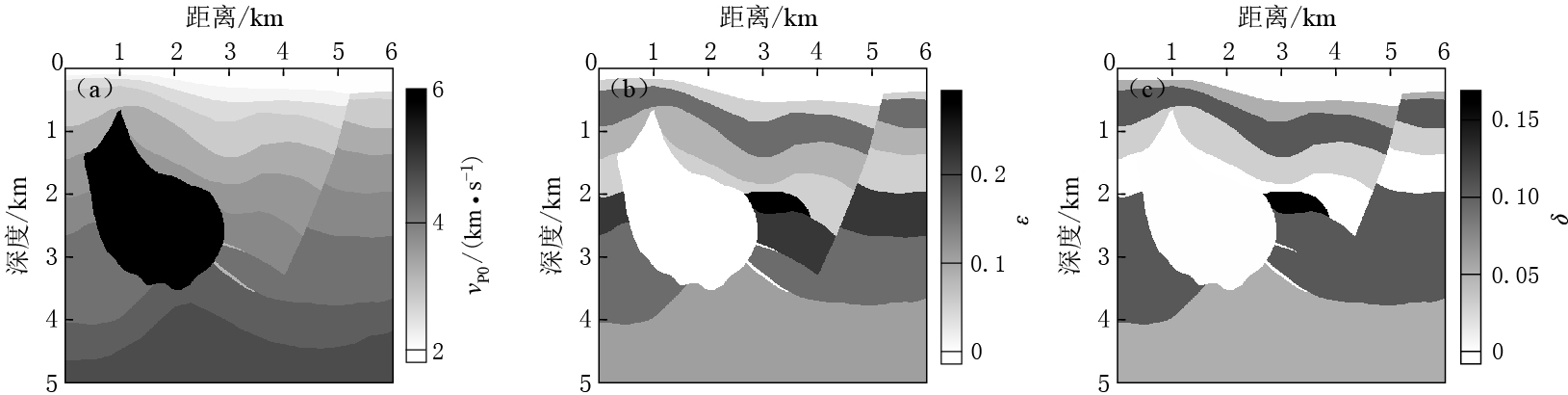
为进一步验证本文方法的准确性,首先用本文的VTI一阶拟声波方程正演模拟方法得到HESS模型的合成地震记录,然后对其进行逆时偏移成像.HESS模型的网格大小为601×501,网格间距为10 m×10 m,其各向异性参数如图 8所示.正演模拟的观测系统为:选用震源主频为30 Hz的雷克子波,采用中间放炮、两边接收的方式;第一个炮点位于模型的(1 500 m,10 m)位置处,总共31炮,每炮301道接收;炮间距为100 m,道间距为10 m;时间采样间隔Δt=1 ms,总采样时间为4 s.分析对比两种偏移结果可知:由于各向异性因素的影响,常规的各向同性声波逆时偏移方法成像效果较差,特别是陡倾角断层及各向异性较强的区域(图 9a);而利用VTI介质拟声波逆时偏移方法则能够准确地刻画地下各向异性构造和陡倾角断层,如图 9中红色方框所示区域.
5. 讨论与结论
从声学近似的VTI介质胡克定律和频散关系两种思路出发,对比分析了3种不同形式的VTI介质一阶拟声波方程,并利用交错网格高阶有限差分法实现了VTI介质一阶拟声波数值模拟,然后通过旋转坐标系将其推广到TTI介质中.相比于四阶和二阶形式,一阶拟声波方程形式简单,易于结合交错网格技术得到精确的正演模拟结果.波场快照验证了本文推导的PML边界条件能够达到理想的边界反射吸收效果.最后,从VTI介质拟声波方程的解析解出发,简单讨论了其固有的qSV人为干扰波的产生机制,并通过设置震源环的方法实现了对干扰波噪音的有效压制.
数值结果表明,3种一阶拟声波方程在运动学和动力学上是等价的,它们均能比较准确地模拟各向异性介质中qP波的运动学(旅行时和速度等)特征,这便于研究qP波的传播规律.结合计算效率分析可知,相对于各向异性弹性波正演模拟,拟声波正演模拟不仅节省了计算内存、效率更高,同时克服了前者的弹性参数意义不明确、波场分离困难等缺陷.设置小区域的震源环能够有效地压制人为干扰波,且不会对有效qP波造成较大影响.由于各向异性因素的影响,地震记录的波场特征(旅行时和振幅等)会发生一定变化,特别是远偏移距处这种影响更为明显,进而会影响偏移和反演的精度.因此,在实际大偏移距、宽方位地震资料的应用中,各向异性因素不能忽略.
本文采用震源环方法虽能从震源处实现对人为干扰波的有效压制,但其难以处理波传播过程中散射源新产生的干扰噪音.因此,人为干扰波的压制方法还有待完善,各向异性介质中纯qP波模式的波动方程及其正演模拟方法也将是今后的研究重点.
衷心感谢审稿专家和编辑部对本文提出的宝贵意见和建议;感谢中国石油大学(华东)Leon课题组的帮助.
-
图 2 波场快照对比(t=400 ms)
(a)VTI介质弹性波方程正演得到的垂直应力分量波场;(b)用式(2)正演得到的波场q;(c)用式(6)正演得到的波场p;(d)用式(7)正演得到的波场p
Figure 2. Comparison of wavefield snapshots (t=400 ms)
(a)Wavefield of vertical stress component modeled by elastic wave equation in VTI media;(b)Wavefield q modeled by equation(2);(c)Wavefield p modeled by equation(6);(d) Wavefield p modeled by equation(7)
图 4 设置震源环前后各向异性介质拟声波正演的波场快照对比(t=400 ms)
(a)VTI介质(设置震源环前);(b)VTI介质(设置震源环后);(c)TTI介质(设置震源环前,θ=45°);(d)TTI介质(设置震源环后,θ=45°)
Figure 4. Wavefield snapshots comparison of anisotropic pseudo-acoustic wave modeling without and with source box (t=400 ms)
(a)VTI media (without source box);(b)VTI media (with source box);(c)TTI media (without source box, θ=45°);(d)TTI media (with source box, θ=45°)
图 6 单炮地震记录对比
(a,d)用式(2)正演得到的炮记录;(b,e)用式(6)正演得到的炮记录;(c,f)用式(7)正演得到的炮记录;(g)TTI介质拟声波方程正演得到的炮记录;(h)VTI介质弹性波方程正演得到的炮记录;(i)各向同性声波方程正演得到的炮记录.其中,(a)-(c)为设置震源环前的结果;(d)-(f)为设置震源环后的结果
Figure 6. Comparison of single shot seismic records
(a,d) Shot records modeled by equation (2);(b,e) Shot records modeled by equation (6);(c,f) Shot records modeled by equation (7);(g) Shot records modeled by TTI pseudo-acoustic wave equation;(h)Shot records modeled by VTI elastic wave equation;(i) Shot records modeled by isotropic acoustic wave equation. Figs.(a)-(c) are results without source box, and Figs.(d)-(f) are results with source box
图 7 单道地震信号对比
(a)从图6a,b,c中近偏移距(地面位置为1 200 m)处抽取的单道信号对比;(b,c)从图6d e,f中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比;(d,e)从图6f,h中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比;(f,g) 从图6f,g,i中近偏移距(地面位置为1 200 m)和远偏移距(地面位置为200 m)处抽取的单道信号对比
Figure 7. Comparison of single trace seismic signals
Fig.(a) is single trace signals comparison of near offset (distance=1 200 m) extracted from Figs.6a,b,c; Fig.(b) and (c) are single trace signals comparison of near offset (distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6d,e,f; Figs.(d) and (e) are single trace signals comparison between near offset (distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6f, h; Figs.(f) and (g) are single trace signals comparison between near offset(distance=1 200 m) and far offset (distance=200 m) extracted from Figs.6f, g, i
表 1 几种波动方程的计算效率对比
Table 1 Computational efficiency comparison of the several wave equations
方程类型 计算量 平均计算时间/s VTI一阶拟声波方程(2) ∂p/∂x,∂q/∂z,∂u/∂x,∂w/∂z 72 VTI一阶拟声波方程(6) ∂p/∂x,∂p/∂z,∂u/∂x,∂k/∂z,∂w/∂z,∂ζ/∂z 105 VTI一阶拟声波方程(7) ∂p/∂x,∂p/∂z,∂q/∂x,∂q/∂z,∂up/∂x,∂wq/∂z 103 各向同性声波方程 ∂p/∂x,∂p/∂z,∂u/∂x,∂w/∂z 70 VTI弹性波方程 ∂τxx/∂x,∂τxz/∂z,∂τxz/∂x,∂τzz/∂z,∂vx/∂x,∂vx/∂z,
∂vz/∂x,∂vz/∂z130 -
Du X, Fletcher R, Fowler P J. 2008. A new pseudo-acoustic wave equation for VTI media[C]//70th EAGE Conference and Exhibition. Rome: European Association of Geoscientists and Engineers: 1-5.
Duveneck E, Milcik P, Bakker P M. 2008. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[C]//SEG Technical Program Expanded Abstracts. Las Vegas: Society of Exploration Geophysicists: 2186-2190.
Zhang H, Zhang G. 2009. Removing S-wave noise in TTI reverse time migration[C]//79th International Exposition and Annual Meeting, SEG. Houston: Society of Exploration Geophysicists: 1-5.
Zhou H, Zhang G, Zhang Y. 2006. An anisotropic acoustic wave equation for VTI media[C]//68th EAGE Conference and Exhibition. Vienna: European Association of Geoscientists and Engineers: 1-5.
-
期刊类型引用(4)
1. 陈利新,王胜雷,万效国,苏洲,马兵山. 哈拉哈塘地区共轭走滑断裂差异特征及演化. 西南石油大学学报(自然科学版). 2024(04): 19-37 .  百度学术
百度学术
2. 曾庆才,王清华,曾同生,陈胜,张凯. 基于测井修正的TTI伪弹性波逆时偏移优化方法. 西南石油大学学报(自然科学版). 2024(04): 38-50 .  百度学术
百度学术
3. 秦宁. VTI介质角度叠加逆时偏移. 石油地球物理勘探. 2019(02): 341-347+237-238 .  百度学术
百度学术
4. 李振春,杨富森,王小丹. 基于LS-RSGFD方法优化的横向各向同性(TI)介质一阶qP波高精度数值模拟. 地球物理学报. 2016(04): 1477-1490 .  百度学术
百度学术
其他类型引用(6)





 下载:
下载: