引 言

自弹性回跳理论提出以来，人们逐渐认识到地震的发生与断层存在密切关系，随后准静态位错理论(简称位错理论)逐渐成为断层地震震源机制解的核心．现代地震研究中的震源机制、地球内部构造、断层反演、大地测量结果解释、震源参数确定和地震预报等都需要建立在精细完善的位错理论基础上．因此，位错理论的重要性不言而喻(孙文科，2008)．自Steketee(1958)将位错理论引入地震学以来，该理论被广泛应用于地震同震、震后的应力、应变和倾斜等研究中(Chinnery， 1961，1963，1965；Berry，Sales，1962；Maruyama，1964；Press，1965；Mansinha，Smylie，1971; 陈运泰等， 1975，1979；Yamazaki，1978；Iwasaki，Sato，1979；李兴才，陈运泰，1982；Davis，1983；Matsu′ura，Iwasaki，1983)．随后Okada(1985，1992)总结了一套半空间均匀位错模型的计算公式，成为位错理论发展的一个里程碑．为使该模型更加符合地球特征，诸多研究者致力于半空间分层模型的研究，通过不同的方法得到地球分层的效果(Thomson，1950；Haskell，1953；Sato，1971；Sato，Matsu′ura，1973)．Wang 等(2003，2006)所发展的半空间分层模型软件包(EDGRN/EDCMP和PSGRN/PSCMP)，将半空间分层位错模型推向成熟．此后，球位错模型的发展不仅考虑了地球分层的影响，而且囊括了地球曲率的影响，在对远场(100 km以外(Pollitz，1996))的计算中相对于前两者明显提高了计算精度，然而该计算的繁琐性影响了其发展(Sun，1992；Sun，Okubo，1993；付广裕，孙文科，2012a)．本文对半无限空间位错模型和球位错模型分别进行分析，对两者的发展进程及其在地震研究方面的差异进行总结，最后对地震位错理论的应用研究成果进行讨论．

1.   半无限空间位错理论

1.1   均匀介质模型

Steketee(1958)首先将位错理论引入地震学中，在各项同性介质内穿过断层面Σ的位错Δu_i(ξ₁，ξ₂，ξ₃)所产生的位移场可表示为

式中：δ_jk为克罗内克符号，λ和μ为拉梅常数，v_k为断层面法向矢量分量，上述几个量均为已知量；u_i^j为在点(ξ₁，ξ₂，ξ₃)处振幅为F的点源的j分量在点(x₁，x₂，x₃)处产生的i分量位移，该表达式由Press(1965)给出． 之后，许多研究人员深入研究了半无限空间均匀介质中的变形问题．Chinnery(1961，1963)给出了垂直于地面的走滑断层的位移与应力场表达式，并在此基础上进一步研究了垂向变形的性质(Chinnery，1965). Berry和Sales(1962)给出了水平张性断层的位移表达式，Maruyama(1964)在其基础上导出了垂直和水平张性断层所引起的地表位移场的完整解析解，Mansinha和Smylie(1971)给出了与地面斜交的走滑和倾滑断层模型下位移场的解析表达式. 陈运泰等(1975)与黄福明和王廷韫(1980)在此基础上分别给出了拉梅常数不相等的情况下，半无限空间弹性介质中任意倾角的矩形斜滑断层所引起的地震位移场与应力场解析表达式. Yamazaki(1978)对膨胀源所产生的变形场进行了研究，陈运泰等(1979)运用大地测量资料反演了唐山地震的位错模式． 赵国光和张超(1981)给出了线性黏弹性半空间中任意倾角的矩形斜滑断层所引起的准静态位移场的完整解析表达式. 李兴才和陈运泰(1982)采用了倾斜断层模式，研究了倾斜断层所引起的应变和倾斜变化．Davis(1983)对倾斜张性断层所导致的形变场进行了分析，并给出了垂向位移的表达式．Matsu′ura和Iwasaki(1983)针对黏弹性介质下同震及震后的地表位移场进行了讨论．

直到1985年，Okada(1985)总结了前人的研究成果，得出一套半无限均匀介质中，剪切和张性断层位错所产生的位移、应变和倾斜的表达式．以走滑位错为例，式(2)给出了点源在每个断层面ΔΣ所引起的位错计算式：

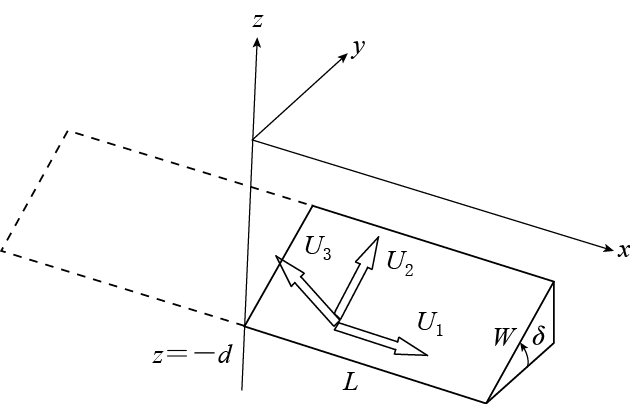
式中，U₁为走滑位错分量，δ为倾角，如图 1所示．图中其它参数含义如下：d为震源深度，L为断层长度，W为断层宽度，U₂和U₃分别为对应任意位错的倾滑和引张位错分量．

图  1  震源模型的几何结构示意图(引自Okada，1985)

Figure  1.  Schematic diagram of geometry of the source model (after Okada，1985)

下载: 全尺寸图片 幻灯片

将u_i^j的表达式(Press，1965)带入式(2)，并取(ξ₁，ξ₂，ξ₃)为(0，0，－d)，即可得到震源在地表所产生的位移，经过微商可进一步得到相应的倾斜和应变．

对于有限矩形位错源，只需将式(2)进行简单变换即可得到最终表达式：

式中p=ycosδ+dsinδ，具体推导过程可参阅Sato和Matsu′ura(1974)、Chinnery(1961)和孙文科(2012)等文章． 在此基础上，Okada(1992)又给出了半无限介质内部的同震应变计算方法.

在实际应用中，由于震源一般较浅，其所引起的、能被观测到的地表变形一般分布在较小的范围内，这就使得地球曲率的影响较小，可以忽略不计．起初，研究人员基于解析公式研究半空间位错理论中相关问题，并作了大量的正反演研究工作(例如，Chinnery， 1961，1963；Berry，Sales，1962；Maruyama，1964；Press，1965；Savage，Hastie， 1966，1969；Mansinha，Smylie，1971；Jovanovich et al，1974a，b；陈运泰等， 1975，1979，2000；Yamazaki，1978；Iwasaki，Sato，1979；黄福明，王廷韫，1980；赵国光，张超，1981；Davis，1983；Matsu′ura，Iwasaki，1983; Chen et al，1996)．1985年后，考虑到Okada(1985)半无限空间模型形式简洁、全面系统、计算方便，因此其成为地震研究中的首选方法(例如，申重阳等，2001；单新建等，2004；王勇等，2004；孙文科，2012)．值得一提的是，Matsu′ura等(1986)基于Okada的理论，发展了负位错模型，其基本假设为块体边界区域的地表位移为刚性块体运动减去由块体边界上部部分锁定导致的地表位移．基于负位错模型可以通过地表位移反演得到块体边界断层带的相对闭锁区，该方法体系对地震中长期预报有重要意义．

在重力研究方面，Okubo(1991，1992)采用类似于Okada(1985)的方法，给出了点源位错和有限矩形位错所产生重力变化的表达式．该表达式与Okada(1985，1992)表达式一起成为研究半空间位错理论的经典表达式．

1.2   分层模型

由于真实的地球介质并不均匀，Okada(1985)模型未考虑地球分层对位错结果的影响(袁旭东等，2007)，因此诸多研究者针对半无限空间层状模型开展了研究(Thomson，1950；Haskell，1953；Wang，1999)．

分层弹性半空间模型更符合实际地球介质结构，其精度明显高于均匀模型. 其求解同震变形的重要途径为利用传播矩阵算法(Thomson，1950；Haskell，1953)解场的微分方程并求得核函数．理论上传播矩阵是可行的，诸多研究者也曾给出利用传播矩阵法计算水平成层介质中点源位错产生的静态位移场(Ben-Menahem，Singh，1968a；Singh，1970；Sato，1971；Sato，Matsu′ura，1973)．但在实际应用中，当进行高频计算或者层与层之间厚度很大时，如果以某一特定入射角进入的波逐渐消散时，传播矩阵法就会变得很不稳定(Ma et al，2008)．为解决这一问题，前人也作了诸多研究(Dunkin，1965；Jovanovich et al，1974b；Müller，1985)． 其中，反射和透射系数矩阵法将4×4阶矩阵转变为2×2阶矩阵来处理(Kennett， 1974，1980；Kennett，Ketty，1979)；离散波数法可以有效求解多个弹性动力学问题中的格林函数(Bouchon，1981)．姚振兴等总结上述两种方法并将其结合，发展了广义反射、透射系数矩阵和离散波数法(Yao，Harkrider，1983；姚振兴，郑天愉，1984)，可以有效地计算近场的格林函数．上述方法相对于传播矩阵法，显著地提高了计算稳定性和求解效率．

另外，Wang(1999)采用正交归一技术，分别对弹性和黏弹性半空间分层模型提出了稳定快速的算法．相对于其它方法，该方法对原始的Thomson-Haskell传播矩阵做了最小的改动，计算效率也相对较高．基于上述计算模式，Wang等(2003，2006)提供了开源的FORTRAN软件包(EDGRN/EDCMP和PSGRN/PSCMP). 由于这两组程序快捷稳定、简单易行，故得到了广泛的应用(李志才等，2005a；单斌等， 2009，2013；谈洪波等，2009；张晁军等，2011)．

2.   球位错理论的发展

半空间位错模型未考虑地球曲率的影响，当计算范围变大时地球曲率的影响已逐渐显现(李志才等，2005b)．球体分层模型是位错理论进一步发展的结果，该模型考虑了地球的曲率和层状构造，显然是更符合地球实际的位错模型．

早在20世纪60年代末，人们就开始对均质无自重球形地球模型进行了理论研究(Ben-Menahem，Singh，1968b；Ben-Menahem et al，1969；Ben-Menahem，Israel，1970)，推导了地球内部位错导致的位移和应变的解析解．计算结果表明，对于浅源地震地球曲率影响在震源距20°以内可以忽略不计，但是地球的层状构造和横向不均匀性可能会有较大影响，由于数值计算等困难他们没有给出震源距2°以内的结果(孙文科，2012)．此外，Saito(1967)提出了球对称层状地球模型的点源自由震荡理论，并给出了源函数，该研究为此后的球形地球位错理论研究奠定了基础．Kagan(1987a，b)进一步给出了各种震源源函数的一般解．

球位错理论的进一步发展则是考虑了地球的黏滞性．Pollitz(1992)研究了黏弹无重力地球模型内位错在震源区域内产生的位移场和应变场；Piersanti等(1995，1997)和Sabadini等(1995)研究了自重黏弹层状地球模型内位错产生的位移场和位移变化率．由于上述研究均基于自由震荡简正模方法，要求地球模型相对简单．当层状地球模型的层数超过一定数量时，计算中出现的简正模数量会急剧增加，从付广裕，孙文科，2012b)．

为了进行更为精确的模拟，Sun(1992)，Sun和Okubo(1993)基于1066A(Gilbert，Dziewonski，1975)以及PREM(Dziewonski，Anderson，1981)模型建立了新的位错理论．该模型定义了位错勒夫数，给出了4个独立点源位错所对应的重力位错格林函数，并在此基础上给出了计算任意类型位错所引起的同震重力位变化与重力变化的总公式．随后，Sun等(1996，2006)将此理论扩展到同震位移和应变研究领域，总结了前期球位错理论的研究进展，排除了前期工作中存在的符号错误，并给出了统一的位错格林函数表达式(Sun et al，2009)．

相对于球体位错理论本身的发展，其计算程序的推广相对滞后．最近付广裕和孙文科(2012a)提供了一套球体位错理论计算程序，为该理论的推广应用提供了条件．该程序主要由3部分组成，可用来计算球对称地球模型中任意地震位错在地球表面所产生的同震位移、应变、大地水准面和重力变化．

球形位错理论的最新研究进展是考虑地球的横向不均匀性．东亚地区的S波速度结构展现出很强的横向扰动(Friederich，2003)；Zhao(2001，2009)在5°×5°空间分辨率情况下所给出的三维P波速度场与球对称模型相比，大约存在1％的横向偏差．上述结果都是利用经典射线理论计算获得，如果利用更高精度的有限频率波动理论计算，其横向扰动的幅度将在此基础上扩大30%左右(Montelli et al，2004)，这在一定程度上反映了地球并非球对称结构．一个符合实际的地球模型应该是自转、微椭、横向不均匀和各向异性的黏弹模型．付广裕和孙文科(2012b)以Molodenskiy(1977，1980)的三维不均匀潮汐理论及Sun(1992)的球对称地球模型位错理论为基础，借助互换定律和扰动方法，推导出一整套计算公式，用来计算三维不均匀地球模型中地震位错所引起的地表及空间固定点同震重力变化和地表同震位移，在一定程度上推动了球位错模型的发展．然而，上述讨论是基于5°×5°三维地球模型，对应于36阶球函数，更为精细的三维地球模型目前仍不存在．孙文科(2012)研究认为，一个更高阶模型会使得横向扰动变大，相应横向不均匀效应也会变得更大．这也是三维地球模型的局限所在，未来仍需要研究更为精细的三维地球模型．

3.   不同位错理论的对比

不同位错理论的比较主要是半空间位错理论与球形位错理论的对比，以及均匀介质、层状介质与横向不均匀介质位错理论之间的比较．前者考虑的是地球曲率的影响，后者考虑的是地球分层的影响．

位错理论的应用主要受地球层状结构和曲率的影响，两者相比之下，分层影响相对较大．袁旭东等(2007)利用同震和震后变形模拟软件包(EDGRN/EDCMP和PSGRN/PSCMP)，以我国唐山M_S7.8和伽师M_S6.8地震为例，在考虑和忽略重力两种条件下，分别采用弹性半空间均匀模型和分层模型，模拟对比了同震地表水平与垂直形变的差异，发现分层对同震变形的影响较大，超出了可观测量级．李志才等(2005b)定量研究了球体分层模型、球体均匀模型和半空间均匀模型在计算不同类型地震断层(走滑断层、逆冲断层)中所产生的地表同震变形差异，结果显示半空间均匀模型与球位错模型的差异显著超出现有测量技术的精度．Pollitz(1996)分析表明，震源附近100 km范围内曲率影响小于2%，当忽略地球层状结构时，计算差异可达20%．除此之外，重力也是位错理论应用中不可忽略的因素之一．Dong等(2014)分别研究了地球层状介质、重力和曲率对同震形变的影响，并进行对比得到层状结构影响最大，重力次之，曲率的影响最小的结论．Amelung和Wolf(1994)研究了表面负荷的球面效应问题，他们比较了考虑重力的球形模型与无重力的半无限空间模型，发现曲率和重力对计算结果都有影响，但同时忽略这两部分时，各自的影响部分相互抵消．此外，震源深度及断层倾角对研究结果也有一定的影响．Sun和Okubo(2002)对比研究了半无限空间地球模型、均质球形地球模型与层状球形地球模型之间的差异，分析了地球曲率和层状构造影响对震源深度的依赖性，结果表明曲率和层状结构影响的大小与震源深度和震源类型有关且不能忽略，其中层状结构影响较大，量值可达25%；另外，地球曲率效应和层状构造效应均随震源深度增加而增加，深源地震导致的较大差异主要来源于地球层状构造的影响．Fu等(2010)通过2008年汶川地震和2004年苏门答腊地震比较了半无限空间位错理论与球位错理论之间的差异，结果表明由于断层倾角的不同，曲率与层状结构对汶川地震造成的影响比对苏门答腊地震造成的影响要大(汶川地震断层倾角适中，而苏门答腊地震倾角较小)，忽略该影响会在远场变形计算中导致100%—200%的偏差．值得注意的是，上述研究结果均未考虑研究区域地形的影响．林晓光和孙文科(2014)以2011年日本大地震为例，研究了地形对同震变形计算的影响，结果显示起伏较大的地形及局部地质构造对同震形变的影响均不容忽略．然而目前位错理论还无法考虑到实际地球表面地形的影响．

综上所述，地球分层、重力、地球曲率、地形起伏、震源深度以及断层倾角都会对位错理论的应用产生一定的影响(表 1)．其中，地球分层带来的影响最大，明显超出了误差接受范围；重力影响次之，最高可达11%(Dong et al，2014)；曲率影响在近场(100 km以内)影响较小可以忽略，但在远场计算中需考虑；震源深度主要通过改变地球层状结构带来的差异来间接影响位错模型的应用；地形的影响虽然较大，但由于位错理论的局限性，在研究过程中无法考虑实际地球表面地形的影响．其中地球分层与曲率直接影响位错理论的应用效果，震源深度与断层倾角主要是通过增加或减小曲率及分层所带来的差异来间接影响位错理论的应用．根据不同因素对位错理论的影响程度进行对比，可以得到不同位错模型的特点及适用条件，如表 2所示．

表  1  位错理论应用的影响因素

Table  1.  Influence factors of dislocation theory in application

影响因素	影响程度	特点
地球分层	≤25%	如果对结果精度要求不高可以忽略，如半空间均匀模型
重力	≤11%	影响程度介于地球分层与曲率之间
地球曲率	≤5%	在近场(100 km以内)影响较小可以忽略
地表起伏	未知	由于位错理论的局限性，目前仍无法考虑实际地球表面地形的影响
震源深度与断层倾角	较小	通过增加或减小曲率及分层所带来的差异来间接影响位错理论的应用

下载: 导出CSV 

| 显示表格

表  2  不同位错模型的特点及适用条件

Table  2.  Characteristics of different dislocation models and their applicable conditions

模型种类	特点	适用条件
半空间均匀模型	不考虑地球层状结构及曲率，使用简单方便，无法考虑地形影响，精度偏低	使用简单，适用于近场且对精度要求不高的研究
半空间分层模型	不考虑地球曲率影响， 使用相对简单，无法考率地形影响，精度相对均匀模型较高	未考虑地球曲率影响，适用于近场研究
球位错模型	考虑地球曲率及层状结构，使用复杂，精度相对半空间模型较高	使用较为复杂，适用于曲率影响无法忽略的远场研究

下载: 导出CSV 

| 显示表格

4.   地震位错理论的应用研究进展

4.1   同震研究

位错理论发展之初主要应用于同震研究中，基于Okada(1985，1992)公式，只需知道震源深度、断层位错量和介质拉梅常数等物理量就可以通过计算得到同震位移、应变和倾斜等结果，如果应用分层半空间模型还需知道分层状态等．近年来，位错理论的应用向更广泛的领域拓展．在对2013年芦山地震的研究中，Wang等(2013)应用半空间位错模型，得到了芦山地震引起的同震、震后位移场和重力场变化，认为芦山地震是一次逆冲型地震. 这与武艳强等(2013)利用GPS观测资料反演得到的结果基本一致，但后者认为芦山地震除了主要的逆冲性质外，还具有细微但较为显著的左旋走滑特征．同时Jiang等(2014)也发现了相同的特性，他们利用近场GPS资料作约束进行同震位错反演，获得的模型位移场与GPS观测结果相吻合，并与余震区显示的破裂面基本相符，所得到的断层滑动虽以逆冲为主，但带有少量左旋成分；同时该研究还发现，即使是芦山地震这样破裂尺度不大的地震，采用分层介质模型并考虑介质的横向非均匀性对结果仍然是有影响的；相比半空间均匀模型，考虑介质横向不均匀性使得滑动角向正逆冲方向偏转了3°，使断层滑动面更靠近余震分布面，该结果对认识芦山地震和龙门山断裂带南段的构造特征有一定意义．此外，在其它地震研究方面，Chen等(2011)基于Okada(1985，1992)半空间位错理论，得到了2011年日本大地震地表位移场和应变场分布．郝金来和姚振兴(2012)基于均匀弹性水平层状介质，发展了利用广义反射透射系数矩阵和离散波数计算同震位移的方法，使之可以计算应变和同震库仑应力的变化．Bai等(2010)采用Okada(1985，1992)模型模拟了2008年汶川地震的垂直和水平同震位移场，发现垂直位移具有明显的不均匀性，其最大位移在断层末端．对于远场研究，球位错模型具有更高的精度. Fu和Sun(2010)应用球位错理论和地震断层模型，计算了2004年苏门答腊地震在四川-云南地区所引起的水平位移分布，发现该结果与GPS观测结果具有一致性，同时还给出了苏门答腊地震导致中国大陆及其周边地区的同震位移、应变、重力和大地水准面的变化. 付广裕(2008)应用球体位错理论计算了汶川地震导致的三峡坝区和北京地区的同震位移、应变、重力和大地水准面的变化，结果表明：汶川地震在三峡坝区产生的位移约为2004年苏门答腊地震的一半，应变为其2—3倍；在北京地区产生的形变总体比苏门答腊地震小1—2个量级．总之，位错理论对地震同震所引起的位移和应变等变化已较为成熟．同时，在应用位错理论时，要注意地球介质的不均匀性等特征，以便得到较好的结果．

4.2   震前、震后研究

随着位错理论的发展，其在震前与震后形变场和重力场研究中也得到了广泛的应用．程佳等(2009)利用半空间弹性三维断裂位错模型，反演了2001年昆仑山口西地震前各断裂带的运动速率．李志才等(2005a)采用黏弹性地球模型计算了唐山地震后28年所产生的形变场．王丽凤等(2013)利用分层模型，应用PSGRN/PSCMP软件计算了2011年日本大地震后的形变场．

地震前后会产生地球重力场的局部变化，这一变化被认为是由断层运动引起地壳形变的结果．燕乃玲等(2003)研究了用有限矩形位错模型计算地壳形变引起的地面重力场变化的方法；谈洪波等(2009)基于有限矩形位错理论模拟计算了黏弹分层半空间条件下汶川地震产生的同震和震后地表变形和重力变化．

负位错模型也是进行震前、震后研究的重要方法．张希等(2009)利用负位错模型反演得到了2008年汶川地震与攀枝花地震震前周边断裂的变形特征与应变积累特征；赵静等(2012，2013)利用GPS速度场数据和负位错理论反演得到了汶川地震和芦山地震前龙门山断裂带闭锁程度和滑动亏损分布，结果表明汶川地震前龙门山断裂带中北段的闭锁深度明显比南段深，该结果有助于理解汶川地震破裂过程往北东方向发展，以及芦山地震震级小、破裂范围窄等特点．

4.3   与其它理论结合研究

在海啸研究中，位错理论也发挥着重要作用．赵曦(2011)将Okada(1985，1992)模型与完全非线性高阶频散性波希涅斯克(Boussinesq)方程结合，建立了海啸生成、传播及爬高的数值模型．其研究流程为先通过位错模型模拟海底的地震过程，再利用高阶波希涅斯克方程描述底面运动引起的水面波动．该方法可以有效地计算自由表面对底面运动过程的响应，并能很好地反映底面的垂向运动形式．

在反演断层滑动速率时，位错理论还可以与粒子群算法结合．段虎荣等(2010)基于位错理论模型，针对所模拟的水平位移观测值分别采用PSO算法、遗传算法以及蒙特卡罗算法对断层的三维滑动速率进行了对比分析；张秀霞(2010)利用Okada(1985，1992)位错模型，结合遗传算法进行正反演研究，分析了龙门山断裂带和榆木山断裂的断层走滑、倾滑和拉张运动分量．总之，位错理论在与其它理论结合时，是采取对同一研究的两个部分分别进行计算，然后进行综合分析的过程，可以达到相互促进的目的．

5.   讨论与结论

地震位错理论在计算地震产生的同震变形，包括位移、倾斜、应变、大地水准面和重力变化，以及解释大地测量观测结果等方面发挥了重要作用．然而，在具体应用中，则应根据各位错模型的特点和适用条件的不同，有效地使用合适的模型．

1)对于均匀介质半空间位错理论，Okada(1985，1992)给出的表达式是该理论发展的一个里程碑. 该表达式具有数学上的简洁性和解析性，此后诸多研究都是基于此进行的．另一方面，该表达式未考虑地球分层和曲率的影响，在精确度方面有其局限性．因此，在具体应用中如果计算效率是首要考虑因素且研究范围距震源区较近，Okada(1985，1992)模型是一个较好的选择．

2)对于半空间分层介质模型，其虽未考虑地球曲率的影响，但是考虑了分层介质因素，相对于Okada(1985，1992)模型在精确度方面更具优势．因此，对于近场的位错计算来说，地球曲率影响较小，基于分层介质模型的半空间位错理论是最佳选择．

3)对于层状球位错模型理论，虽然表达式相对复杂，计算效率较低，但其既考虑了地球分层的影响，又考虑了地球曲率的影响．因此，对于远场计算来说，应优先考虑采用层状球位错模型．

4)地震位错理论的最新进展是考虑了地球的横向不均匀性．横向不均匀性更加符合实际地球的物质分布形态，其计算精度虽有所提高，但是距实际应用还有一段距离．目前应用广泛的球位错模型并没有考虑这一点．

5)地震位错理论还在继续发展中，一些物理问题应该进一步加以考虑．例如，更详细的三维构造模型、考虑时间变化的黏性构造和地形的影响等．另一方面，重力观测研究将会更加深入并得到更广泛的应用(邹正波等，2008；Zheng et al，2008；Li，Shen，2011；姜磊等，2014)．这些理论与观测的发展和进步也将促进地球内部构造、地震断层反演以及各种大地测量数据解释等方面的研究．

6)在计算同震形变方面，位错理论对于地球三维结构及介质不均匀性等因素的考虑还不够充分．在实际计算方面其它的方法也是不错的选择，如有限元数值模拟方法等(朱桂芝等，2003；丰成君等，2013)．