The strain energy accumulating-releasing period and strong earthquake prediction in Sichuan-Yunnan rhombic block
-
摘要: 将川滇菱形地块分为两个地块, 分别以形变确定应变速率、 深部速度构造确定弹性模量、 联合地块体积确定地块应变能积累与时间的关系, 结合历史强震研究应变能积累释放周期以及该周期内的强震活动, 进而研究应变能积累释放与强震活动的关系. 结果表明, 地块应变能积累释放存在周期性并可预测强震震级. 在应变能积累前期, 没有强震(M≥7.0)发生; 随着时间增加, 应变能继续增加, 地块上先后发生几次强震, 但每次强震震级均小于预测震级, 即一次强震只释放了一部分能量; 而后应变能积累继续增加, 直到一、 二次特大强震(M≥7.5)发生, 将绝大部分应变能释放. 至此, 老的周期结束, 新的周期开始. 应变能积累从小到大直到最后完全释放的周期性导致了地震的平静活跃周期, 地震活跃期比平静期长得多. 本文认为, 大区域地理范围因其含有多个地块, 不宜讨论其地震平静活跃周期, 而对于小范围单次强震也不宜讨论其复发周期. 虽然活跃期中的强震从时间上看并无任何规律, 但利用活动地块应变能的积累释放曲线所预测的震级与实际震级很接近. 本文结果对于地震安全性评价工作可能有重要意义.Abstract: In this paper, the Sichuan-Yunnan rhombic block is divided into two parts. The strain rate is achieved by deformation, the elastic modulus is acquired by velocity structure in the deep, the volume of the block is calculated by the area and thickness of block, and then the variation of accumulated strain energy with time is confirmed. On this basis, combined with the research of historical strong earthquakes, the relationship between the period of energy accumulating-releasing and the seismic activity is obtained. The results show that the strain energy accumulating-releasing emerges periodically, which can be used for strong earthquake prediction. The strong earthquakes (M≥7.0) do not occur at initial stage of strain energy accumulation. The strain energy increases continuously with time and then several strong events occur firstly, but each event is smaller in magnitude than the predicted ones, i.e., one event releases a small part energy and later energy increases incessantly. The energy is not completely released until one or two great strong events (M≥7.5) occur. Thus, the old cycle ends and a new cycle starts. Obviously, the quiet to active periods are caused by the cycle of strain energy accumulation from small to great, and then to completely releasing. Active stage is much longer than the quiet one. Therefore, it is unsuitable to discuss the quiet-active period for a great geographic area covered by many blocks or to discuss the repeat period of single strong earthquake for a small region. Although the occurrence of strong earthquakes does not obey any law in time, the magnitude predicted by the strain energy accumulating-releasing curves is coincident with the real one, which may be significant for seismic safety evaluation.
-
引言
地磁场是重要的地球物理场之一,由地核场、地壳磁场、变化磁场和感应磁场等4部分构成(傅承义等,1985;徐文耀,2009).地磁学是以观测为基础的学科,地磁场基础观测数据直接或间接地用于地球基本磁场及其长期变化、地球外部空间电磁环境监测,以及震磁关系和地震预报等方面的研究,并为其它测量手段(如航海、地球物理勘探等)提供通化标准.因此,地磁观测数据不仅具有学术研究意义,而且是不可或缺的国家基础战略资源(徐文耀,2003).
截至2014年,我国已基本建成了由160个观测台站组成的覆盖全国的数字化地磁前兆观测网络,实现了观测数据的准实时传输和自动汇集,积累了大量的高精度观测数据,这些数据被广泛应用于地震前兆、地球和太阳活动及地磁场模型等研究中. Ida等(2012)和冯志生等(2013)利用地磁观测数据分析了不同地震前的地磁场变化特征; Li等(2009)、王源等(2010)和赵旭东等(2010)等利用地磁观测数据研究了磁暴和Sq电流体系的变化特征; Gu等(2006)和陈斌等(2012)等利用台站观测数据进行了地磁场模型的研究.因此,完整的高精度地磁数据不仅服务于地磁学本身,更是地震、地质构造、地球深部和矿产勘探等研究的基础.
然而,在地磁台站观测中通常会由于仪器故障、仪器定向和雷击等因素的影响而出现数据记录缺失的情形.数据缺失时间通常较长,多为数小时到数天,这不仅影响了数据的完整性,同时也会对数据分析结果造成很大影响.因此,在数据缺失的情况下,尽可能不失真地重构观测数据、保证数据的可用性,对地磁数据分析具有重大意义.
目前地震学上常用的数据重构方法有3种:①基于预测滤波理论的频率域(f-x域)插值方法(Spitz,1991)和抗假频频率-波数域(f-k域)插值方法(Gulunay,Chambers,1996);②基于波场传播理论并结合动力波动方程,正常时差校正(normal moveout,简写为NMO)与逆倾角时差校正(dip moveout,简写为DMO)联合的重构方法(Ronen,1987);③基于数学变换的重构方法,例如非均匀傅里叶变换(高建军等,2009)、曲波变换重构非规则缺失数据方法(Herrmann,Hennenfent,2008; Naghizadeh,Sacchi,2010)等.然而,对于地磁数据重构方法的研究却很少. 姚法章(1988)曾将订正法应用于绝对观测数据填补的研究中,即利用魏尔德(Wild)公式将多年对应缺数月份的均值作为订正参考值,基于该订正值对缺失数据的数值进行估计.然而,地磁相对记录主要受空间电流体系的影响(徐文耀,2009),磁场活动水平不同,相对记录数据差异较大,无法将多年的数据用于缺失数据填补,因此订正法不适用于相对记录数据. 朱兆才(1989)利用地磁观测数据在空间上的较高相关性,将相邻单台数据与缺失台站数据进行回归分析,提出了利用回归方程填补缺失数据的方法. Lockwood等(2013)在重现过去167年地磁活动性与近地行星际关系的研究中,利用简单的最小二乘拟合法将附近单台数据用于缺失数据的填补,取得了较好的结果.因此,邻台重构是值得尝试的方法,但由于单个邻台数据质量限制以及日变形态差异等因素,仅用一个台站来进行缺数重构无法保证重构精度.鉴于此,本文将在考虑地磁相对记录空间相关性及日变差异的情况下进行多台数据重构,将不同的权重赋予不同的邻近台站,利用空间加权的方法尽可能不失真地重构数据,以保障数据的可用性.
1. 数据重构原理与方法
地球变化磁场起源于地球外部并叠加在基本磁场上的各种短周期地磁变化.产生变化磁场的根本原因在于固体地球外部的各种电流体系,除一些特殊的磁异常区以外,地球表面一个局部小区域内若干点的地磁变化主要受同源影响并具有相似性(朱兆才,1989).各台站记录到的变化磁场在时间上具有较好的同步性,且相关性较强,因此本文利用缺数台站(以下称为目标台站)附近台站(以下称为参考台站)的数据进行加权拟合,重构缺失数据,称之为空间加权法.
1.1 地磁空间相关性
本文以观测质量较好的红山台(LYH)为中心,选取距其400-4 000 km范围内、跨越其东西两侧且观测质量较好的蒙城台(MCH)、乾陵台(QIX)、长春台(CNH)、德都台(DED)、拉萨台(LSA)、乌鲁木齐台(WMQ)和喀什台(KSH)等7个台站进行地磁相对记录数据的相关分析,台站分布如图 1所示.这7个台站与红山台的距离分别为478.52,662.73,1 132.70,1 543.96,2 357.50,2 448.48和3 372.79 km.各台站相对记录数据与红山台记录数据之间的相关性如图 2所示,可以看出:两台站间的相关性与其间距Δ基本成反比,Δ越小,相关系数C越大;当Δ≤1 000 km时,地磁相对记录具有较高的空间相关性,C>0.9,并且随着Δ增大,相关性降低.因此,为了确保参考台站与目标台站之间具有较高的相关性,须满足Δ < 1 000 km.
![]() 图 1 秒数据台站及本研究所使用台站分布图.大圆圈为距红山台750 km的范围Figure 1. The distribution of stations with one-second data and those used in this studyOpen triangels represent all stations, solid triangles represent reference stations, the star is target station, and the great circle represents the range of 750 km centered on the station LYH
图 1 秒数据台站及本研究所使用台站分布图.大圆圈为距红山台750 km的范围Figure 1. The distribution of stations with one-second data and those used in this studyOpen triangels represent all stations, solid triangles represent reference stations, the star is target station, and the great circle represents the range of 750 km centered on the station LYH地磁日变依赖于地方时,位于不同地理经度的台站间的地磁日变形态有相位差,称为日变延时. 冯志生等(2005)的研究表明,相位随经度的延时约为4 min/°.相位延时同样会影响重构结果,因此参考台站与目标台站的距离应尽量选择在半个时区(750 km)以内,即任意两参考台站间的地方时差不超过1 h.综合台站的空间相关性及日变延时因素,本文认为在以目标台站为圆心、半径为750 km的范围内进行参考台站选取较为合理,如图 1中大圆圈所示.此外,为了抵消日变相位差的影响,各参考台站与目标台站的经度差之和越接近零越好.若以目标台站为原点,向东为正,向西为负,则有

(1) 式中,N为参考台站个数,λ0为目标台站地理经度,λi为参考台站地理经度.
1.2 数据重构原理
空间加权法中最重要的部分是各参考台站权重的确定.在确定各台站权重前,本文作了以下3个假设:
1)在不考虑台站数据质量的情况下,假设台站间相关系数与其间距成反比关系,即

(2) 式中,ki为第i个参考台站的比例系数,Ci为目标台站与第i个参考台站的相关系数,Ri为两台站间距,c为常数.在地磁空间相关性的研究中,两台站间的相关性与其间距基本成反比,间距越小,相关系数越大,其变化关系可用简单线性拟合.
2)在式(2)的基础上,假设各参考台站的权重因子与其到目标台站的距离Δ成反比,间距越大,权重越小,即

(3) 式中, Wi为第i个台站分配的权重.目标台站数据并不是由单一台站数据拟合而来,而是由各台站加权拟合得到.
3)假设各台站间观测值为线性关系,即

(4) 式中,Ki为拟合系数,y0为目标台站数据,yi为第i个参考台站数据,ci为常数.对于单个台站(目标台站)的记录数据,均可以利用其附近任一台站(参考台站)的数据进行线性拟合,拟合关系表达式为式(4).
地磁场强度一般为几万nT左右(刘佳等,2007),而正常日变幅度仅为几十nT,若仪器动态范围较大,则其分辨力会降低.为了记录地磁场的微弱变化,提高磁力仪的分辨力,通常会在磁通门仪器探头上加补偿线圈,这样就会产生一个与地磁场大小相同、方向相反的补偿磁场,使探头铁芯近似工作于零场状态,在地磁观测技术上称为仪器补偿(胡星星等,2010).然而,由于仪器的补偿差异,各台站相对记录数据在形态上相似,但在数值上却相差较大,如图 3所示.为避免由于仪器补偿导致的输入数据量级差别较大而造成的较大重构误差,在数据重构前先将各台站数据进行归一化处理,归一化公式的表达式为

(5) 式中,yij为归一化后第i个参考台站的第j个数据,Bmin和Bmax分别为非缺失记录数据中的最小值和最大值,Bij为归一化前第i个参考台站的第j个数据.
由式(1)-(4)可得

(6) 式中,Yj为第j个归一化后的重构数据,r为残差项.将Yj反归一化即可得重构数据Bj.
1.3 台阶改正
虽然式(1)确保了参考台站与目标台站之间的经度差较小,但经度差为零的情况几乎不存在,日变形态差异所造成的相位延时对数据重构仍有影响,数据形态在重构前后表现为首尾台阶差,如图 4所示.
![]() 图 4 2013年7月1日红山台线性台阶改正结果Figure 4. The result of linear-step correction of the station LYH on 1 July, 2013The thin black line indicates original data, the thick black line indicates reconstruction data before linear-step correction and the thick grey line indicates reconstruction data after linear-step correction
图 4 2013年7月1日红山台线性台阶改正结果Figure 4. The result of linear-step correction of the station LYH on 1 July, 2013The thin black line indicates original data, the thick black line indicates reconstruction data before linear-step correction and the thick grey line indicates reconstruction data after linear-step correction为保证数据的连续性,采用线性台阶改正的方式进行台阶补偿,其表达式为

(7) 式中,B′j为最终重构结果,M为缺失数据个数,dB1为加权后的首台阶差,dB2为加权后的尾台阶差.
2. 数据仿真
为了计算空间加权法的重构精度并检验该方法的适用性,本文进行了数据仿真.以红山台(LYH)为目标台站,假设缺失该台站其中一套仪器GM4-1一整天的数据,将另一套仪器GM4-2的数据作为参考,以距其750 km为半径的范围选取参考台站,如图 1所示.考虑到观测数据质量及相位延迟互补,选取泰安(TAA)、榆林(YUL)、蒙城(MCH)和乾陵(QIX)等4个台站作为参考台站进行加权数据重构,各台站与红山台(LYH)的距离分别为253.1,454.4,478.5和662.7 km,经度差之和为7.3°.
在利用红山台另一套仪器GM4-2进行重构时,因参考台站与目标台站为同一台站,权重设为1,仅利用归一化和反归一化便可重构缺失数据.由于不涉及日变相位差,故不进行台阶改正.
为了分析磁场活动程度对空间加权法的影响,对2013年所有静日和扰日的数据进行了仿真.利用绝对残差R计算其重构精度,其表达式为

(8) 式中,f(n)为地磁台站原始观测信号,
 表 1 不同季节静扰日重构残差Table 1. The residuals of reconstruction of quiet and disturbed days in different seasons
表 1 不同季节静扰日重构残差Table 1. The residuals of reconstruction of quiet and disturbed days in different seasons季节 日期 静/扰日 空间加权重构残差/nT 同台重构残差/nT D H Z D H Z 春秋季 2013-03-08 静日 0.10 0.19 0.12 0.10 0.25 0.27 2013-03-17 扰日 0.36 0.32 0.36 0.40 0.84 0.56 2013-04-19 静日 0.09 0.15 0.12 0.10 0.15 0.21 2013-04-24 扰日 0.20 0.22 0.21 0.28 0.34 0.29 2013-09-28 静日 0.08 0.08 0.10 0.12 0.19 0.22 2013-09-19 扰日 0.17 0.12 0.18 0.27 0.32 0.16 2013-10-05 静日 0.07 0.08 0.12 0.15 0.16 0.10 2013-10-02 扰日 0.31 0.22 0.40 0.76 0.66 0.28 夏季 2013-05-29 静日 0.12 0.15 0.15 0.10 0.34 0.29 2013-05-01 扰日 0.25 0.19 0.28 0.18 0.41 0.38 2013-06-26 静日 0.14 0.14 0.13 0.10 0.22 0.38 2013-06-01 扰日 0.34 0.27 0.36 0.16 0.20 0.51 2013-07-02 静日 0.13 0.14 0.15 0.10 0.30 0.27 2013-07-06 扰日 0.19 0.17 0.21 0.17 0.27 0.43 2013-08-29 静日 0.09 0.10 0.12 0.33 0.28 0.15 2013-08-16 扰日 0.21 0.22 0.24 0.43 0.50 0.23 冬季 2013-01-22 静日 0.08 0.10 0.10 0.08 0.18 0.17 2013-01-26 扰日 0.15 0.17 0.17 0.17 0.13 0.15 2013-02-06 静日 0.08 0.11 0.12 0.10 0.14 0.10 2013-02-14 扰日 0.12 0.14 0.14 0.14 0.17 0.12 2013-11-25 静日 0.08 0.09 0.12 0.14 0.15 0.09 2013-11-11 扰日 0.16 0.13 0.20 0.47 0.21 0.13 2013-12-02 静日 0.08 0.10 0.10 0.10 0.17 0.14 2013-12-08 扰日 0.23 0.18 0.28 0.62 0.17 0.22 静日均值 静日 0.10 0.12 0.12 0.13 0.21 0.20 扰日均值 扰日 0.24 0.23 0.23 0.34 0.35 0.29 总均值 0.16 0.16 0.19 0.23 0.28 0.24 注:D为磁偏角,H为水平分量,Z为垂直分量. 将不同季节静扰日的仿真结果列于表 1,可以看出:磁扰日的重构绝对残差R高于磁静日,空间加权法重构残差低于同台重构残差,空间加权法重构残差约为0.15 nT,与仪器分辨力(0.1 nT)相当,低于台站背景噪声水平(0.2 nT)(姚休义,2015),重构精度较高;在季节变化上,夏季的重构残差最大,春秋季与冬季基本持平,冬季略低于春秋季.究其原因,均与磁场活动水平有关. 袁亚红等(2012)的研究结果也表明,地磁活动呈现出显著的季节变化特点,夏季活动最强,春秋季次之,冬季活动最弱.因此,重构精度也随着磁场活动程度或季节变化而有所不同.此外,因外源感应“电流源”均位于地表附近且“电流源”相对于地表是水平的,或位于仪器附近且与仪器处于同一水平面,根据毕奥-萨法尔(Biot-Savart)定律,仪器感应到的异常主要体现在垂直分量Z,因此Z分量与地下结构的联系最为紧密,最能反映地下结构或观测环境的变化(丁鉴海等,1994;李琪等,2006),但其对外源电流体系变化的反应弱于D和H分量,故Z分量的重构残差较D和H分量的重构残差略大.
图 5和图 6分别以2013年12月2日和2013年2月14日为例,给出了静扰日重构数据与原始数据的对比.从图 5a可以看出,磁静日的两条曲线几乎完全重合,各分量重构数据与原始数据的相关系数几乎为1,重构结果很好.从图 5b可以看出,三分量的重构残差基本在零线附近波动,其平均重构残差R分别为0.08,0.10和0.10 nT,均不高于仪器分辨力0.1 nT;利用红山台另一套仪器GM4-2得到的平均重构残差分别为0.10,0.17和0.13 nT.因此,在磁静日利用空间加权方法得到的重构残差低于同台重构残差,且低于仪器分辨力,这说明利用空间加权法进行静日地磁数据重构是可行的.
磁扰日的重构效果略低于磁静日,尤其是在磁扰剧烈的时刻,如图 6所示.可以看出,D,H,Z分量均在6时11分的磁扰最为剧烈,磁场变化较快,D和H分量的残差约为±1 nT,Z分量残差却达2.7 nT,其它磁扰时段的残差值基本在零线附近波动.通过考察各参考台站当日的数据记录发现,泰安、榆林两台站的Z分量在6时11分产生的磁扰与蒙城、乾陵两台站呈反向,如图 7所示.正是Z分量反向造成其平均重构残差较大,其原因可能与该地区地下结构变化所导致的电导率异常有关(徐文耀等,1978).当天的D,H和Z分量重构残差R分别为0.12,0.14和0.14 nT,利用红山台另一套仪器GM4-2得到的平均重构残差分别为0.14,0.16和0.12 nT,D和H分量的空间加权重构残差均低于同台重构残差,而Z分量的加权重构残差略高于同台重构残差,故本文认为Z分量残差较大与参考台站泰安与榆林、蒙城与乾陵在磁扰时段的Z分量反向有关.磁扰日重构残差高于磁静日,虽然与同台重构结果相比其精度仍较高,但在磁扰剧烈时段,尤其当电导率异常区域两侧的磁扰曲线出现相位反向时,重构残差较大.因此,针对重构中出现的磁扰时段单个残差较大的情况,确实需要考虑空间加权法在磁扰时段的适用性.
3. 重构检验
重构数据与原始数据的重叠及其较低的重构残差在一定程度上保证了重构数据的高精度,然而数据重构过程中是否遗漏或丢失了某些重要信息则是数据重构需要验证的一个问题.为了确保空间加权法的适用性,本文分别计算了原始数据和重构数据的Welch功率谱(Welch,1967).从频率域对原始相对记录数据和重构数据进行分析,图 8给出了静扰日的原始相对记录数据和重构数据的三分量功率谱密度.可以看出:原始相对记录数据和重构数据的功率谱密度均表现出低频能量高于高频的特点;在f < 0.2 Hz的低频范围内极为一致,在f>0.2 Hz的高频噪声部分有细微差别.另外,计算了原始数据功率谱密度与重构数据功率谱密度之间的相关系数,磁静扰日各分量的功率谱密度相关性高达1.0,呈显著相关;垂直分量Z相关性略低,是由局部电性结构差异造成各台站感应场不同所致.空间加权法重构数据是各参考台站感应场的平均效果,所以与原始数据之间略有差异,该差异主要集中在高频部分(浅层),多为噪声成分,观测台站不同,其噪声水平也不同.总之,当对数据高频部分要求不高时,利用空间加权法进行数据重构是可行的.
4. 讨论与结论
本文在对地磁相对记录数据的空间相关性的研究基础上,将空间加权法应用于地磁相对记录数据的缺失重构.通过数据仿真和检验,得到以下结论:
1)空间加权法重构精度受地磁活动性影响.不同季节、不同地磁活动程度下的重构残差变化表明,磁场活动越平静,重构残差越小,重构精度越高.磁静日的平均重构残差为0.11 nT,磁扰日的平均重构残差为0.23 nT.
2)空间加权法重构残差低于同台站重构残差.在利用空间加权法进行数据重构时,选取同台站另一套仪器的数据进行对比研究的结果表明,在大部分重构结果中,尤其是在磁静日时,空间加权法重构残差低于同台重构残差.
3) D和H分量的重构残差小于Z分量. Z分量受地下结构影响较D和H分量大,故Z分量的重构残差略大,重构效果较D和H分量略差.
4)重构数据与原始数据功率谱密度相关性较好.原始记录数据与重构数据的功率谱密度的对比研究表明,重构信号与原始记录信号在频域内能达到较大程度的完整重构,遗漏或错构数据较少.但是,由于各台站噪声水平差异,尤其是数据采集过程中产生的仪器噪声不一致会导致高频部分略有差异.
值得注意的是,空间加权法虽然在绝大多数情况下能取得较好的重构结果,但当地磁活动中出现急变型剧烈磁扰时,因空间加权法重构残差较大,对此类磁扰事件不建议使用空间加权法进行重构.此外,空间加权法对信号高频部分的重构能力较差,对重构后的数据也不建议使用其高频部分.空间加权法虽然在地磁数据重构过程中显示了重构精度高、信号完整度强、计算速率快的优点,但重构数据毕竟属于非真实数据,可用于背景研究或解决数据处理中因缺数造成的计算问题,但不能作为异常进行提取,尤其在震磁异常分析时,须避开该段重构数据的异常特征.
-
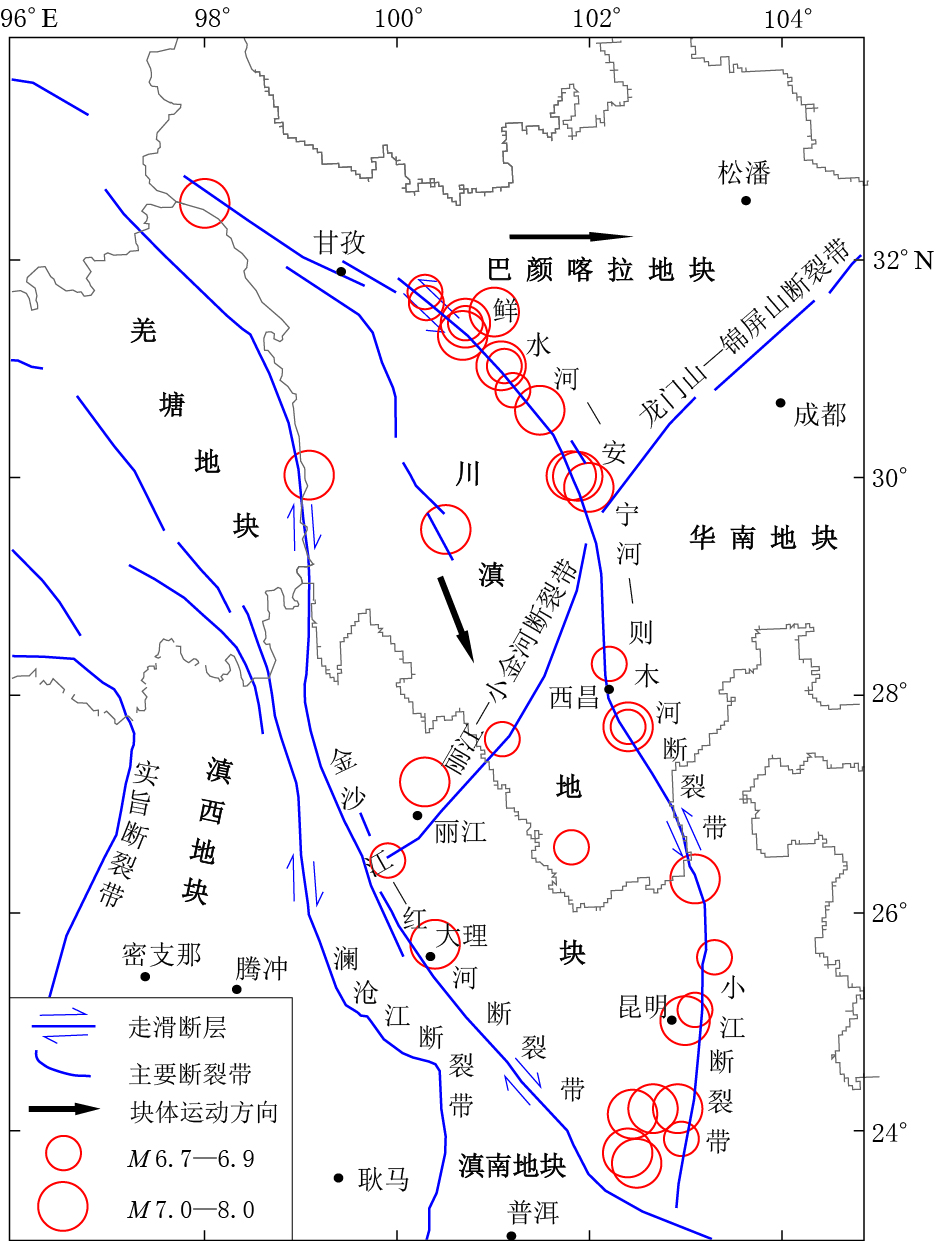
图 1 川滇菱形地块地质构造图及1700年以来M≥6.7强震分布图(引自皇甫岗等,2010)
Figure 1. Geological sructure of Sichuan-Yunnan rhombic block and distribution of strong earthquakes (M≥6.7) since the year 1700 (after Huangfu et al, 2010)
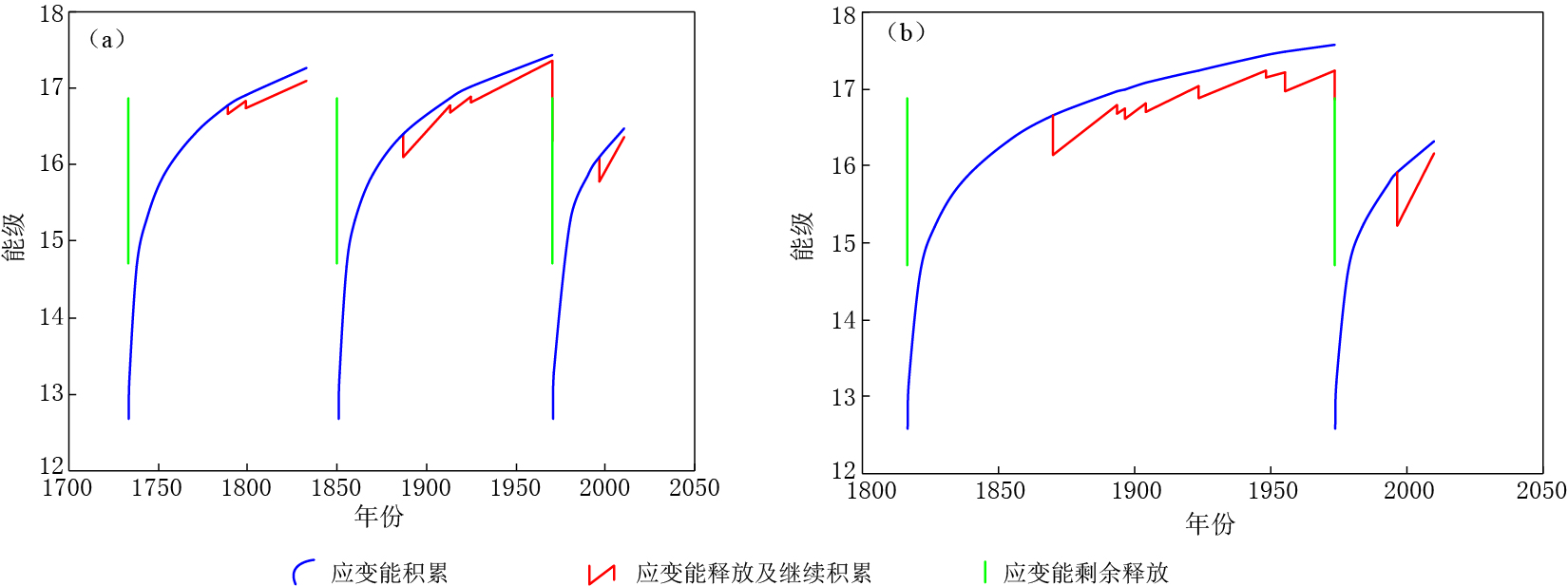
图 3 川滇菱形地块东南地块(a)和西北地块(b)应变能积累释放周期及强震活动曲线, 图中纵坐标为对实际积累的应变能取对数的结果
Figure 3. The period of strain energy accumulating-releasing and seismicity curves in southeastern (a) and northwestern (b) Sichuan-Yunnan rhombic block, where the ordinate represents the result by taking logarithm of actual accumulated strain energy
表 1 川滇菱形地块东南地块强震震级(M≥7.0)与用应变能积累释放曲线所预测震级的比较
Table 1 Comparison of the magnitudes of strong earthquakes (M≥7.0) with those predicted by strain energy accumulating-releasing curve in southeastern Sichuan-Yunnan rhombic block
周期 年份 震级 北纬/° 东经/° 发震地点 能级 预测震级 第一周期 1733 7 ¾ 27.7 102.4 云南东川紫牛坡 1789 7 24.2 102.9 云南华宁路居 16.792 7.445 1799 7 23.8 102.4 云南石屏宝秀 16.862 7.492 1833 8 25.0 103.0 云南嵩明—杨林 17.233 7.739 第二周期 1850 7 ½ 27.7 102.4 四川西昌—普格 1887 7 23.7 102.5 云南石屏 16.432 7.205 1913 7 24.2 102.5 云南峨山 16.814 7.460 1925 7 25.7 100.4 云南大理 16.927 7.535 1970 7.8 24.2 102.7 云南通海 17.388 7.843 注: 能级为对实际积累的应变能取对数的结果, 下同. 表 2 川滇菱形地块西北地块强震震级(M≥7.0)与用应变能积累释放曲线所预测震级的比较
Table 2 Comparison of the magnitudes of strong earthquakes (M≥7.0) with those predicted by strain energy accumulating-releasing curve in northwestern Sichuan-Yunnan rhombic block
年份 震级 北纬/° 东经/° 发震地点 能级 预测震级 1816 7 ½ 31.4 100.7 四川炉霍 1870 7 1/4 30.0 99.1 四川巴塘 16.672 7.365 1893 7 30.6 101.5 四川道孚乾宁 16.805 7.454 1896 7 32.5 98.0 四川石渠洛须 16.765 7.427 1904 7 31.0 101.1 四川道孚 16.823 7.466 1923 7 1/4 31.5 101.0 四川炉霍—道孚 17.053 7.619 1948 7 1/4 29.5 100.5 四川理塘 17.249 7.750 1955 7.5 30.0 100.4 四川康定—折多塘 17.247 7.748 1973 7.6 31.3 100.7 四川炉霍 17.273 7.766 注: 1816年四川炉霍M7 ½ 地震至1973年四川炉霍MS7.6地震为应变能积累释放的一个周期. -
许绍燮. 1982. 地震活动性图象述评[C]//大陆地震活动和地震预报国际学术讨论会论文集. 北京: 地震出版社: 3-29. Xu S X. 1982. A review of the seismicity patterns[C]//A Collection of Papers of International Symposium on Continental Seismicity and Earthquake Prediction (ISCSEP). Beijing: Seismological Press: 3-29 (in Chinese).
尹祥础. 2011. 固体力学[M]. 北京: 地震出版社: 58-65, 388-427. Yin X C. 2011. Solid Mechanics[M]. Beijing: Seismological Press: 58-65, 388-427 (in Chinese).
Kanamori H. 2001. Energy budget of earthquakes and seismic efficiency[C]//Earthquake Thermodynamics and Phase Transformations in the Earth's Interior, International Geophysics Series, Volume 76. San Diego, California: Academic Press: 293-305.
Scholz C H. 1996. The Mechanics of Earthquakes and Faulting[M]. 2nd ed. New York: Cambridge University Press: 1-504.
-
期刊类型引用(9)
1. 赵乃千,郭宇鑫,廖绍欢,李雪浩. 成都地铁运营对成都地震中心站地磁观测的干扰分析. 地震地磁观测与研究. 2023(01): 67-73 .  百度学术
百度学术
2. 居海华,张乐,夏忠,张岑,应允翔. 基于铯光泵磁力仪的地震地磁矢量测量系统. 仪器仪表学报. 2023(09): 111-120 .  百度学术
百度学术
3. 王彬,李延峰,马文来,许正霖,罗宾生. 地磁剖面异常二维拟合算法研究. 高原地震. 2022(02): 58-65 .  百度学术
百度学术
4. 居海华,夏忠,宫杰,应允翔,张岑. 基于分体悬挂式球形线圈的质子矢量磁场测量仪. 仪器仪表学报. 2022(07): 17-25 .  百度学术
百度学术
5. 程文凯,杜劲松,陈超,艾萨·伊斯马伊力. 基于XGBoost机器学习的地磁日变重构方法研究. 地震学报. 2021(01): 100-112+136 .  本站查看
本站查看
6. 何朝博,滕云田,胡星星. 光泵磁力仪频率信号高精度测定技术实现. 地震学报. 2021(02): 245-254+136 .  本站查看
本站查看
7. 顾慧冬,姚休义,李东林. 基于空间加权法的地磁数据重构精度与D_(st)指数的关系. 地震地磁观测与研究. 2020(03): 91-97 .  百度学术
百度学术
8. 姚休义,滕云田,杨冬梅,姚远. 基于神经网络的地磁观测数据重构研究. 地球物理学报. 2018(06): 2358-2368 .  百度学术
百度学术
9. 严吉,樊冬,程文坤,李章. 泾县及周边地磁空间地震磁效应分析研究. 华南地震. 2018(04): 61-66 .  百度学术
百度学术
其他类型引用(4)





 下载:
下载: