Daily variation model of the geo-electric field based on the geo-electric data from the regional geo-electric observation networks
-
摘要: 应用泰勒多项式和曲面样条函数法建立了我国地电场观测台网中华东、 华北两个区域台网的地电场日变化(Kp≤5)模型，并对拟合结果进行了对比分析. 结果表明： ① 尽管地电场变化复杂，但用这两种方法建立的日变化模型相当吻合，模型曲线随时间的变化符合样本曲线随时间的变化; ② 用模型曲线可以描述其它年份同农历日期、 同等磁情时实测的地电场日变化; ③ 用模型曲线描述实测地电场日变化时，低磁情时得出的结果要优于高磁情时的结果; ④ 用多日样本曲线得到的模型曲线更能清晰地展示出地电场日变化的两次起伏波形、 幅度以及极值集中在午前午后等变化特点. 今后建立全国各区域台网不同磁情、 不同农历日期的地电场日变化模型可定量评价区域台网的地电场观测资料的质量，同时根据该模型能够分离出地电场的非正常变化，进而研判真实的异常，以服务于地震等灾害事件的预测以及地球电磁环境变化的监测等方面.Abstract: The planar and time-varying models (geomagnetic index Kp≤5) of the daily variation of the geo-electric field in two regional geo-electric networks in East China and North China are built up based on the Taylor polynomial and surface spline function methods, respectively. Then the fitting results are compared and analyzed. The results show that although the geo-electric field variation is more complex, the models of the daily variation fitted by the two methods are identical to each other, and the two model curves are consistent with the measured sample curves with the variation of time. The two model curves could be used to describe the measured daily variation on the same lunar date in other years with the similar geomagnetic index Kp. The daily variation results based on the two models on the condition of a low geomagnetic index are better than that on a high geomagnetic index. The average model curves based on multi-day sample curves more clearly show the daily variation features of geo-electric field such as the twice fluctuation waveform in some day and its amplitude and the extreme value concentrating on before and after noon. It is important to establish the daily variation models of geo-electric field for the different lunar date in the different geomagnetic indices in each regional network. The models can be used to quantitatively evaluate the quality of observation data of regional geo-electric field networks, and the geo-electric field anomaly measured by the networks can be picked up based on these models, which can be applied to prediction of disasters like earthquakes and monitoring the changes in the electromagnetic environment.
-
引言
场地卓越周期是描述场地特性的重要指标． 地表土层对不同周期的地震波有选择放大作用，致使在地震记录图上显示某些周期的波形特别多且好，即显得“卓越”，故称为地震卓越周期(《岩土工程手册》编写委员会，1994)． 确定场地卓越周期的方法有以下3种(童广才，刘康和，2000): ① 当场地内有强震动记录时，通过频谱分析确定； ② 由常时微动测试分析确定； ③ 根据场地分层剪切波速测试结果按其子层周期求和公式计算． 前两种方法均是通过确定场地的地震动卓越周期以进一步确定场地的卓越周期． 高广运等(2000)和陈鹏等(2009)将卓越周期分为记录卓越周期Tr、 测试卓越周期Tm和波速卓越周期Tv． Tr为真实反应地震动的卓越周期(利用地震动卓越周期间接反映场地卓越周期，该周期也在不同程度上受到地震震源谱特性和区域地壳介质对地震波传播的影响)，当工程场地范围内有适宜的强震动记录时，抗震设计应首选Tr; Tm为接近场地固有周期的卓越周期; Tv为与场地固有周期相比有一定误差的卓越周期，除非地基土层基本满足均匀平行的条件，否则应尽量避免选用．
场地卓越周期在数值上与卓越频率互为倒数，因此卓越周期可由卓越频率求倒得出． 目前日本强震动观测台网KiK-net记录中既有场地地下记录(NS1，EW1，UD1)，也有地表记录(NS2，EW2，UD2)，因此对场地内强震记录通过频谱分析确定其卓越频率时可以采用以下3种方法： ① 地表记录的傅里叶谱分析法； ② 地表水平/垂直傅里叶谱比法(Wen et al，2006； 任叶飞等，2013)； ③ 地表/地下傅里叶谱比法．
本文拟选取日本强震动观测台网中两个基岩台站和两个Ⅲ类场地台站的数百条记录，分别采用上述3种方法对两个基岩台站和两个Ⅲ类场地台站的卓越频率进行分析，并对比分析各种方法的优缺点及其适用情况．
1. 强震动数据
本文从日本强震动观测台网中选取了FKOH06和KGSH03两个基岩台站以及TCGH16和IBRH17两个Ⅲ类场地台站，这些台站分别有地表和相应的地下观测点，各台站分别获得了大量的地震事件记录． 在选择台站地震动记录时，对地震事件随机选取，但是需注意所选的地震动记录峰值加速度的分布应尽量能覆盖各个等级． 最终用于本文研究的强震动记录为： FKOH06台站29次地震事件的地表和地下记录，共174条； KGSH03台站25次地震事件的地表和地下条记录，共150条； TCGH16台站45次地震事件的地表和地下记录，共270条； IBRH17台站33次地震事件的地表和地下记录，共198条．
2. 数据分析
首先使用ViewWave软件读取地震记录，该软件默认对记录进行滤波和基线校正； 其次进行傅里叶变换，分别绘制出各条记录的傅里叶谱以及地表/地下和地表水平分量/垂直分量的傅里叶谱比曲线，读取傅里叶谱最大幅值以及傅里叶谱比曲线中谱比最大值所对应的频率值，即为卓越频率； 然后分别绘制出各场地经上述3种方法分析得到的卓越频率的散点分布图； 最后对比卓越频率的分布情况，分析在确定场地卓越频率时各方法的适用性．
图 1—6给出了FKOH06和KGSH03两个基岩台站所在场地的卓越频率分布． 由图 1和图 4可以看出，基岩台站地下和地表记录的3个分量的傅里叶谱卓越频率分布均很分散． 由图 2和图 5可以看出，台站所在场地的地表水平/垂直傅里叶谱比卓越频率分布也都很分散． 由图 3和图 6可以看出，场地的水平分量和垂直分量的地表/地下傅里叶谱比卓越频率分布不同： 对于FKOH06台站所在场地，水平分量南北向和东西向卓越频率分布比较分散，而垂直分量卓越频率分布相对集中； 对于KGSH03台站所在场地则得到相反的结论． 综上，对于基岩场地卓越频率，上述3种方法所得结果均很分散，无法给出一个准确的卓越频率值，这表明基岩地震动的卓越周期主要反映的是地震震源谱特性和区域地壳介质对地震波传播的影响，而局部基岩场地对地震动卓越周期的影响则不明显．
![]()
图 1 基岩台站FKOH06所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布 图中数字1和2分别表示地下和地表， 下同Figure 1. The distribution of Fourier spectrum dominant frequency in the site of bedrock station FKOH06 on the underground (a) and surface (b) The numbers one and two represent the underground and surface， respectively， the same below![]()
图 2 基岩台站FKOH06的地表水平/垂直 傅里叶谱比卓越频率分布Figure 2. The distribution of surface horizontal/ vertical Fourier spectral ratio dominant frequency in bedrock station FKOH06![]()
图 3 基岩台站FKOH06的地表/地下 傅里叶谱比卓越频率分布Figure 3. The distribution of surface/underground Fourier spectral ratio dominant frequency in bedrock station FKOH06![]()
图 4 基岩台站KGSH03所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布Figure 4. The distribution of Fourier spectrum dominant frequency in the site of bedrock station KGSH03 on the underground (a) and surface (b)![]()
图 5 基岩台站KGSH03的地表水平/垂直 傅里叶谱比卓越频率分布Figure 5. The distribution of surface horizontal/ vertical Fourier spectral ratio dominant frequency in bedrock station KGSH03![]()
图 6 基岩台站KGSH03的地表/地下 傅里叶谱比卓越频率分布Figure 6. The distribution of surface/underground Fourier spectral ratio dominant frequency in bedrock station KGSH03图 7—12为Ⅲ类场地台站的卓越频率分布图. 由图 7和图 10可以看出: Ⅲ类场地台站TCGH16和IBRH17地下记录的3个分量的傅里叶谱卓越频率分布比较分散； TCGH16台站地表水平分量的傅里叶谱卓越频率分布比较集中，约为4.47 Hz，而其垂直分量的傅里叶谱卓越频率分布比较分散； IBRH17台站地表水平分量和垂直分量的傅里叶谱卓越频率分布均比较集中，分别约为8.96 Hz和10.26 Hz． 由图 8和图 11可以看出，TCGH16台站所在场地的地表水平/垂直傅里叶谱比卓越频率分布比较集中，约为4.53 Hz，而IBRH17台站所在场地则比较分散． 由图 9和图 12可以看出，TCGH16和IBRH17台站所在场地的地表/地下傅里叶谱比卓越频率分布均比较集中，其所在场地的水平分量的地表/地下傅里叶谱比卓越频率分别约为4.54 Hz和9.35 Hz，相应垂直分量约为11.29 Hz和11.39 Hz． 由上述结果可知： 对于TCGH16台站所在场地，3种方法均能给出一个相对确定的卓越频率值，分别为4.47 Hz，4.53 Hz和4.54 Hz； 对于IBRH17台站所在场地，地表水平/垂直傅里叶谱比卓越频率分布比较分散，而由地表记录傅里叶变换所得到的卓越频率为8.96 Hz，由地表/地下傅里叶谱比法得到的卓越频率为9.35 Hz．
![]()
图 7 TCGH16台站所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布Figure 7. The distribution of Fourier spectrum dominant frequency in the site of station TCGH16 on the underground (a) and surface (b)![]()
图 8 TCGH16台站的地表水平/垂直 傅里叶谱比卓越频率分布Figure 8. The distribution of surface horizontal/ vertical Fourier spectral ratio dominant frequency in station TCGH16![]()
图 9 TCGH16台站的地表/地下傅里叶 谱比卓越频率分布Figure 9. The distribution of surface/underground Fourier spectral ratio dominant frequency in station TCGH16![]()
图 10 IBRH17台站所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布Figure 10. The distribution of Fourier spectrum dominant frequency in the site of station IBRH17 on the underground (a) and surface (b)![]()
图 11 IBRH17台站的地表水平/垂直傅里叶 谱比卓越频率分布Figure 11. The distribution of surface horizontal/ vertical Fourier spectral ratio dominant frequency in station IBRH17![]()
图 12 IBRH17台站的地表/地下傅里叶 谱比卓越频率分布Figure 12. The distribution of surface/underground Fourier spectral ratio dominant frequency in station IBRH173. 讨论与结论
对于基岩台站FKOH06和KGSH03所在场地，由3种方法所得的卓越频率分布均比较分散，无法给出一个确定的数值，初步认为是由于场地岩层坚硬、 局部场地条件对地震动影响较小所致，因此场地地表和地下记录所体现的主要还是地震震源谱特性和区域地壳介质对地震波传播的影响，而场地上不同地震的震源及地震波传播路径存在较大差异，从而导致所得的场地卓越频率分布比较分散．
对于Ⅲ类场地，TCGH16和IBRH17台站所在场地的土层条件不同，上述3种方法在具体场地的适用性也不同． 对于TCGH16台站所在场地，3种方法均能给出一个确定的卓越频率数值，且3种方法所得数值很接近． 对于IBRH17台站的所在场地，地表水平/垂直傅里叶谱比卓越频率分布比较分散，无法给出确定数值，而另外两种方法均可给出确定数值，但数值相差较大． 结合两个台站所在场地的具体土层条件分析，TCGH16和IBRH17台站所在场地土层均为砂层、 砂砾夹有黏土层，但等效剪切波速(前者172 m/s左右，后者272 m/s)及覆盖土层厚度(前者约75 m，而后者深达235 m)差别较大，初步认为是地表土层剪切波速及土层厚度的影响所导致的．
综合上述3种方法的分析结果，可以得到如下结论：
1)地表记录傅里叶谱分析法所得的卓越频率所包含信息较多，既有地震震源和区域地壳介质的影响，也有局部场地特性影响． 对于基岩场地，由于场地条件对地震动影响较小，而地震震源和区域地壳介质的影响比较突出，因此同一场地上由不同记录得出的结果偏差较大，如上述两个基岩台站所在场地． 但对于地表有土层的场地，场地条件对地震动影响明显，可以得出较为准确的结果．
2)地表水平/垂直傅里叶谱比法的前提是认为场地条件对地震动垂直分量的影响相对于水平分量要小得多，但当场地地表为较厚土层时，场地条件对地震动垂直分量的影响也较大，因此该方法在某些场地适用(如TCGH16台站所在场地)，但在某些场地所得结果却很分散(如IBRH17台站所在场地)．
3)地表/地下傅里叶谱比法理论上最能反映场地条件对地震动的影响，本文认为该方法所得场地卓越频率是比较准确的． 作者还选取了20次不同地震事件在TCGH16台站的地震动记录与相邻的TCGH12台站的地震动记录进行了对比分析，结果显示两个台站地下记录的傅里叶谱差异很小(图 13)，但在地表差异却较大(图 14)，这说明地表/地下傅里叶谱比法确实能很好地体现场地条件对地震动的影响，从而验证了该方法的准确性．
![]()
图 13 TCGH16(a)和TCGH12(b)台站地下记录的傅里叶谱Figure 13. Fourier spectrum recorded by station TCGH16 (a) and TCGH12 (b) on the underground![]()
图 14 TCGH16(a)和TCGH12(b)台站地表记录的傅里叶谱Figure 14. Fourier spectrum recorded by station TCGH16 (a) and TCGH12 (b) on the surface对于基岩场地，由于局部场地条件的影响相对较弱，地震动频谱中包含的场地特性影 响信息很少，所以3种方法所得结果均很分散； 对于地表存在土层的场地，地表水平/垂直傅里叶谱比法所得结果存在不确定性，而地表/地下傅里叶谱比法则能给出一个相对较为准确的场地卓越频率值．
-
![]()
图 1 天水台地电场NS测道2007年9月10日(a)和2007年8月18日(b)的分钟值曲线
Figure 1. The minute-value curves of geo-electric field in channel NS at the station Tianshui on September 10, 2007 (a) and on August 18, 2007 (b)
![]()
图 2 Ⅰ号区域(a)和Ⅱ号区域(b)地电场台站分布
Figure 2. Distribution of geo-electric field stations in region Ⅰ(a) and Ⅱ(b)
![]()
图 3 大柏舍台和延庆台NS测道2012年4月19—20日(农历3月29—30日，Kp=3)的地电场日变化模型曲线和实测样本分钟值曲线
(a，c) 大柏舍台泰勒多项式和曲面样条函数模型曲线；(e，g) 大柏舍台实测样本曲线；(b，d) 延庆台泰勒多项式和曲面样条函数模型曲线；(f，h) 延庆台实测样本曲线
Figure 3. The minute-value curves of geo-electric field model and measured sample in channel NS at the stations Daboshe and Yanqing on April 19 and 20, 2012 (on Lunar March 29 and 30, Kp=3)
(a) and (c) are the Taylor polynomial and surface spline model curves of the station Daboshe; (b) and (d) are the Taylor polynomial and surface spline model curves of the station Yanqing; (e, g) and (f, h) are the measured sample curves of the stations Daboshe and Yanqing, respectively
![]()
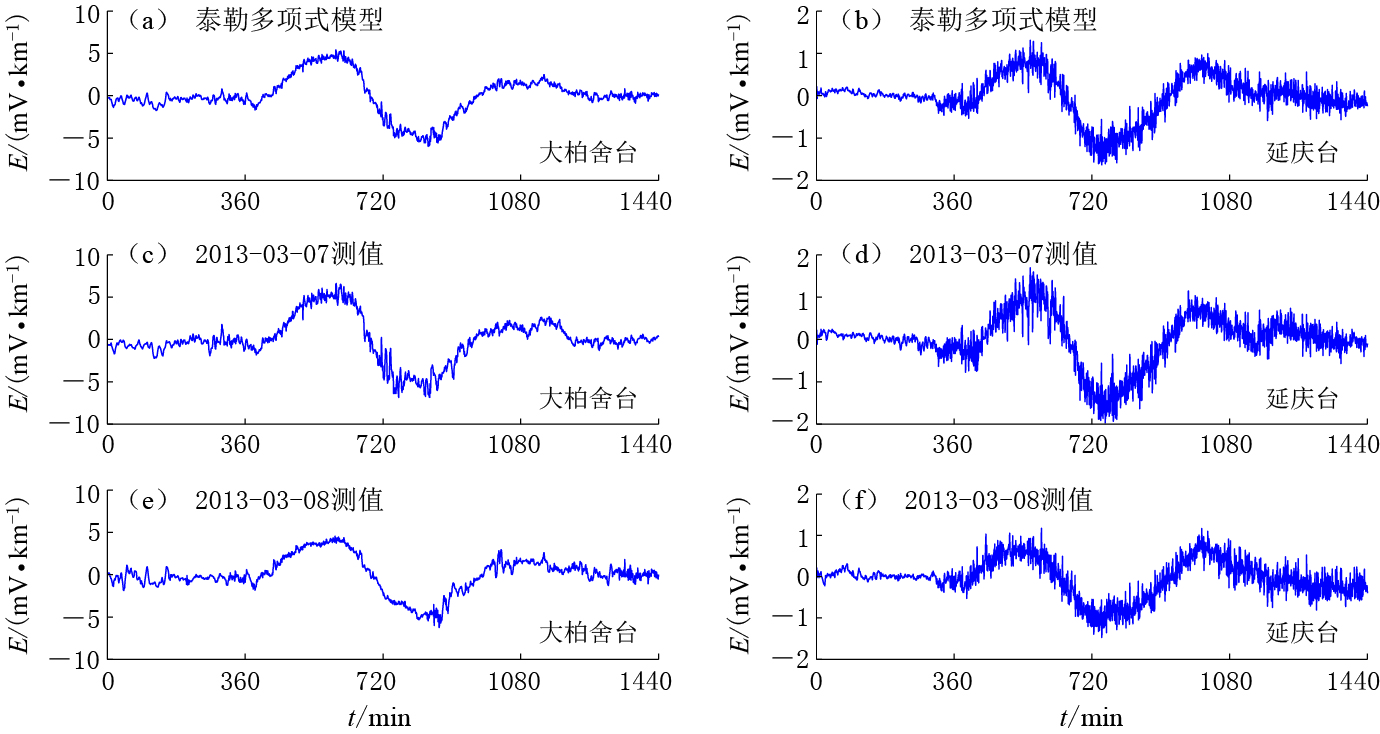
图 4 大柏舍台和延庆台NS测道2013年3月7—8日(农历1月26—27日, Kp=1)的地电场日变化模型曲线和实测样本分钟值曲线
(a, b) 大柏舍台和延庆台泰勒多项式模型曲线；(c，e) 大柏舍台实测样本曲线；(d，f) 延庆台实测样本曲线
Figure 4. The minute-value curves of geo-electric field model and measured sample in channel NS at the stations Daboshe and Yanqing on March 7 and 8, 2013 (on Lunar January 26 and 27, Kp=1)
(a) and (b) are the Taylor polynomial model curves of the stations Daboshe and Yanqing， respectively; (c, e) and (d, f) are the measured sample curves of the stations Daboshe and Yanqing， respectively
![]()
图 5 徐庄子台、 通州台和延庆台NS测道2010年5月29—30日(农历4月16—17日，Kp=5)的地电场日变化模型曲线和实测样本分钟值曲线
(a, b, c) 徐庄子台、 通州台和延庆台泰勒多项式模型曲线；(d，g) 徐庄子台实测样本曲线；(e，h) 通州台实测样本曲线；(f，i) 延庆台实测样本曲线
Figure 5. The minute-value curves of geo-electric field model and measured sample in channel NS at the stations Xuzhuangzi, Tongzhou and Yanqing on May 29 and 30, 2010 (on Lunar April 16 and 17, Kp=5)
(a)，(b) and (c) are the Taylor polynomial model curves of the stations Xuzhuangzi, Tongzhou and Yanqin, respectively; (d, g), (e, h) and (f，i) are the measured sample curves of the three stations, respectively
![]()
图 6 大柏舍台和延庆台NS测道2013年5月8日(农历3月29日，Kp=3)和2014年2月26日(农历1月27日，Kp=1)被描述的实测分钟值曲线
(a，c) 大柏舍台被描述的实测曲线；(b，d) 延庆台被描述的实测曲线
Figure 6. The described minute-value curves of geo-electric field in channel NS at the stations Daboshe and Yanqing on May 8, 2013 (on Lunar March 29, Kp=3) (upper) and on February 26, 2014 (on Lunar January 27, Kp=1) (lower)
(a, c) and (b, d) are the described curves of the stations Daboshe and Yanqing, respectively
![]()
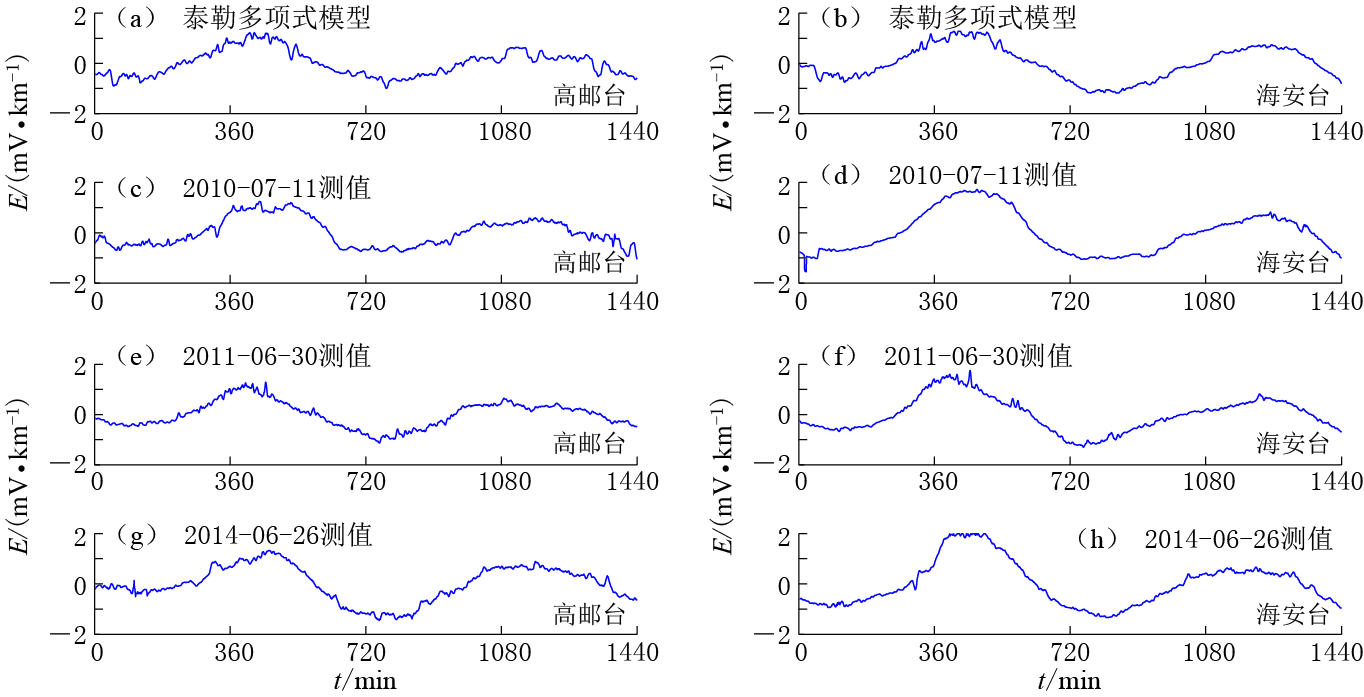
图 7 高邮台和海安台NS测道2012年7月18日(农历5月30日，Kp=1)泰勒多项式模型分钟值曲线及2010年7月11日、 2011年6月30日和2014年6月26日(农历5月30日，Kp=2)被描述的实测分钟值曲线
(a, b) 高邮台和海安台泰勒多项式模型曲线；(c，e，g) 高邮台被描述的实测曲线；(d，f，h) 海安台被描述的实测曲线
Figure 7. The minute-value curves of geo-electric field based on Taylor polynomial model on July 18, 2012 (on Lunar May 30， Kp=1) and described curves in channel NS at the stations Gaoyou and Haian on 11 July 2010, 30 June 2011 and 26 June 2014 (on Lunar May 30, Kp=2)
(a) and (b) are the Taylor polynomial model curves of the stations Gaoyou and Haian, respectively; (c, e, g) and (d, f, h) are the described curves of the stations Gaoyou and Haian, respectively
-
傅承义, 陈运泰, 祁贵仲. 1985. 地球物理学基础[M]. 北京: 科学出版社: 203-254. Fu C Y, Chen Y T, Qi G Z. 1985. Geophysical Foundation[M]. Beijing: Science Press: 203-254 (in Chinese).
克拉耶夫. 1954. 地电原理[M]. 张可迁, 陈培光, 张志诚译. 北京: 地质出版社: 100-236. ΚpaeB A Π. 1954. Geo-electrics Principle[M]. Zhang K Q, Chen P G, Zhang Z C, Trans. Beijing: Geological Publishing House: 100-236 (in Chinese).
李金铭. 2005. 地电场与电法勘探[M]. 北京: 地质出版社: 36-54. Li J M. 2005. Geoelectric Field and Electrical Exploration[M]. Beijing: Geological Publishing House : 36-54 (in Chinese).
孙正江, 王华俊. 1984. 地电概论[M]. 北京: 地震出版社: 3-95. Sun Z J, Wang H J. 1984. Introduction to Geo-electricity[M]. Beijing: Seismological Press: 3-95 (in Chinese).
徐文耀. 2003. 地磁学[M]. 北京: 地震出版社: 221-249. Xu W Y. 2003. Geomagnetism[M]. Beijing: Seismological Press: 221-249 (in Chinese).
曾融生. 1957. 大地电流勘探方法[J]. 地球物理勘探, (2): 1-7. Zeng R S. 1957. The exploration methods of the telluric current[J]. Geophysical Prospecting, (2): 1-7 (in Chinese).
中国地震局. 2006. 地震台站建设规范, 地电观测台站, 第2部分: 地电场台站(GB/T 18.2—2006)[S]. 北京: 地震出版社: 1-7. China Earthquake Administration. 2006. Specification for the Construction of Seismic Station, Geoelectrical Station, Part 2: Geoelctrical Field Observatory (GB/T 18.2—2006)[S]. Beijing: Seismological Press: 1-7 (in Chinese).
中国地震局. 2008. 地震观测仪器进网技术要求, 地电观测仪, 第2部分: 地电场仪 (GB/T 29.2—2008)[S]. 北京: 地震出版社: 1-11. China Earthquake Administratin. 2008. Technical Requirements of Instruments in Network for Earthquake Monitoring-Geoelectrical Meters, Part 2: Meter for Geoelectrical Field (GB/T 29.2—2008)[S]. Beijing: Seismological Press: 1-11 (in Chinese).
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 2004. 地震台站观测环境技术要求, 第2部分: 电磁观测(GB/T 19531.2—2004)[S]. 北京: 地震出版社: 1-16. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. 2004. Technical Requirement for the Observation Environment of Seismic Stations, Part 2: Electromagnetic Observation (GB/T 19531.2—2004)[S]. Beijing: Seismological Press: 1-16 (in Chinese).
-
期刊类型引用(10)
1. 陈钰鑫，李平，高志寅，田兆阳，薄景山，李孝波. 基于地脉动数据的北川老县城河谷场地效应研究. 振动与冲击. 2025(06): 254-262 . 
百度学术
2. 吴雄伟，杨江，夏界宁，范涛. 红沿河核电厂地震仪表系统震后数据分析. 大地测量与地球动力学. 2024(09): 985-990 . 百度学术
3. 李小军，钱玉，荣棉水，孔小山. 基于地震动反应谱与傅里叶谱确定场地卓越频率的差异性. 震灾防御技术. 2024(03): 421-435 . 百度学术
4. 李孝波，宋霖君，宣雨童，吴义文，欧阳刚垒. 基于HVSR和VRSR法的场地地震响应分析. 振动与冲击. 2023(22): 303-311 . 百度学术
5. 兰景岩，宋锡俊，王婷. 上覆海水层对自由场基本周期影响的离心模型试验研究. 岩土工程学报. 2021(04): 768-775 . 百度学术
6. 潘章容，李同林，崔建文，田秀丰，石文兵，张卫东，袁洁. 2021年5月21日云南漾濞M6.4及相关地震强震动记录特征分析. 地震工程学报. 2021(04): 791-798 . 百度学术
7. 黄俊阁，罗永红，王运生，朱兴貌，欧剑锋，张跃跃，南凯. 基于环境噪声测试表征斜坡地震动响应:以自贡西山斜坡为例. 成都理工大学学报(自然科学版). 2020(01): 16-27 . 百度学术
8. 华永超，齐文浩，薄景山，郑桐. 场地周期的确定方法综述. 地震工程与工程振动. 2020(02): 239-251 . 百度学术
9. 戴苗，王秋良，刘坚，黄俊，魏贵春，申学林. 2017-06三峡库区M4.3、M4.1双地震强震记录分析. 大地测量与地球动力学. 2018(01): 18-23 . 百度学术
10. 杜修力，袁雪纯，黄景琦，许紫刚. 典型土层场地随机地震反应规律分析. 震灾防御技术. 2017(03): 574-588 . 百度学术
其他类型引用(15)
下载:
计量
- 文章访问数: 519
- HTML全文浏览量: 218
- PDF下载量: 27
- 被引次数: 25
