Time-dependent probabilistic seismic hazard analysis methods and its applications based on characteristic earthquake models
-
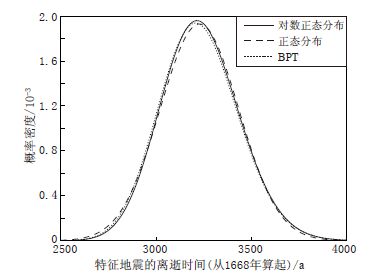
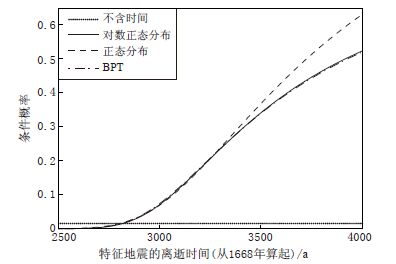
摘要: 本文介绍了特征地震的对数正态分布模型、 正态分布模型和布朗过程时间模型， 提出了使用地震破裂面源模型的特征地震含时间的概率地震危险性分析理论和方法. 通过具体算例对不同的特征地震模型进行了比较， 并对特征地震危险性分析方法进行了系统探索. 研究结果表明， 特征地震含时间模型在复发周期早期的地震危险性低于不含时间模型， 而在后期其地震危险性则高于不含时间模型. 特征地震复发周期的对数正态分布模型与布朗过程时间模型计算得出的地震危险性差别不大. 在未到期望复发时间时， 正态分布模型与前两种模型计算的地震危险性差别不大； 而接近期望复发时间及之后时段， 正态分布模型计算的地震危险性则迅速增大.
-
关键词:
- 含时间的概率地震危险性 /
- 特征地震 /
- 对数正态分布 /
- 布朗过程时间模型 /
- 地震破裂面源模型
Abstract: This paper introduces several kinds of characteristic earthquake models, which obey lognormal distribution, normal distribution and Brownian passage-time (BPT), and then proposes the theory and method of time-dependent probabilistic seismic hazard analysis (PSHA) of characteristic earthquake based on seismic rupture surface model. Finally different characteristic earthquake models are compared through several examples, and the PSHA method of characteristic earthquake are systematically explored. The results indicate that the seismic hazard of time-dependent models of characteristic earthquake in early periods of recurrence cycle is lower than that of time-independent model, and higher than that of time-independent model in later periods. The seismic hazard by using lognormal distribution model is similar to that by BPT model. Before expected recurrence time, the seismic hazard calculated by normal distribution model is similar to the two models mentioned above, but increases quickly near and beyond expected recurrence time. -
引言
高精度重力梯度测量作为一种新兴的地球物理探测技术，不仅在海洋重力辅助导航、 海底潜艇探测和海底资源勘探等领域具有重要意义(徐遵义等，2007； DiFrancesco et al，2009； Araya et al，2011)，而且在陆地资源勘探、 大型水库监测和水底坑洞探测等领域也是一种有效的地球物理探测技术(王谦身，2003; Woolrych et al，2015)． 此外，航空和卫星重力梯度测量在地球重力场等基础科学研究领域也具有重要的作用(宁津生等，1996，2002)．
自1971年美国空军首次提出精度为1 E的移动级重力梯度仪以来，高精度重力梯度仪的研究得到了迅速发展，其主要设计原理为差分加速度计和扭矩测量． 基于差分加速度计的航空重力梯度仪，由于其自身的高稳定性和高精度得到了迅速发展和应用(李红军等，2002； 刘凤鸣等，2009)，但大部分还处于实验样机阶段，目前唯一定型的商用重力梯度仪是美国贝尔实验室研制的旋转加速度计重力梯度仪(DiFrancesco et al，2009)． 基于扭矩测量的重力梯度仪，由于体积和稳定性问题，其发展受到了限制． 彭益武等(2006)设计的基于扭矩测量的二维簧片重力梯度仪在体积和稳定性等方面取得了突破． 另外，超导重力梯度仪由于其测量精度、 体积和整体质量等方面的优势，越来越多地被应用于航空重力测量中(吴琼等，2013)，具有非常好的发展前景(Moody et al，2002)．
上述各类梯度仪的设计原理均属于相对测量，需要对参考坐标及变化的物理量进行标定，不适用于发射到宇宙外星球进行长期的内部质量分布探测研究，因此，在美国宇航局20世纪末的火星探测计划中，Micro-G公司开展了基于激光干涉原理的绝对重力梯度仪的研制，其测量精度的设计指标为1 E，其目的是探测火星的深部结构(Brown et al，1999; Robertson，2001)．
受此启发，激光绝对重力梯度仪作为研究地球深部质量迁移的一种新型有效工具，更能满足地震的监测需求． 目前，我国差分加速度计的最高精度为10-6 m/s2，这与梯度仪要求的测量精度还有很大差距； 而现有的绝对重力测量技术的测量精度可达10-8 m/s2，完全能够满足重力梯度仪的精度要求(胡华等，2012； 滕云田等，2013)，故基于创新设计及软件开发，利用激光干涉法完成地表重力垂直梯度测量的方案是完全可行的． 虽然目前该仪器的体积较大，但从固定台站观测的角度看，该缺点可以忽略； 而且随着激光干涉重力梯度仪研究的进一步开展，将来可以进行小型化设计，使之满足移动重力垂直梯度仪的测量需求．
本文拟基于激光干涉法对新型地表重力垂直梯度测量系统进行研究并初步构建原理样机. 该测量系统采用激光干涉原理，通过测定两个落体同步自由下落时相对于刚性连接的两个参考点的位置信息确定各自的重力加速度，然后通过差分计算得到测点的重力垂直梯度． 由于两个参考点为刚性连接，其感受到地面的振动信息完全相同，且两个落体利用同一套伺服控制系统，由振动引入的测量误差将在差分时消除，这样即可得到某测点的高精度重力垂直梯度值． 与其它重力梯度仪相比，激光干涉重力梯度仪具有以下优点： ① 有较大的测量范围，无需标定，无漂移； ② 地面振动属于共模误差，无需设计特殊的隔振系统，对动态测量非常有利； ③ 地面倾斜属于共模误差； ④ 对地球浅层异常质量体敏感．
1. 设计原理
1.1 基本原理
基于激光干涉法重力垂直梯度测量的基本原理是，当两个落体在一个真空舱中同步自由下落时，运动过程中所受到的干扰因素可以等效为一个合力，并且该合力对每个落体的作用均相同，唯一不同的是所受重力场重力垂直梯度的影响． 因此，通过解算垂直向间隔为h的两个落体(较高位置的为上落体P1，较低位置的为下落体P2)在真空中作自由下落运动时测量得到的干涉条纹，分析重建各自的自由下落轨迹(吴琼等，2012)，并获取上落体P1在其有效测量高度href_U处的第一绝对重力加速度值gU和下落体P2在其有效测量高度href_D处的第二绝对重力加速度值gD，再根据下式得到单次下落的重力垂直梯度γ，即
(1) 图 1给出了重力梯度测量算法原理，主要是为了确定式(1)中的两个未知量href_U和href_D． 落体P1的初始位置为A00，其对应的初始速度和位移均为0，但在实际工作中一般将初始速度和位移无限接近于0的A0点作为其初始位置，在计算中近似认为A00与A0重合，因此hinst_U对应的是P1的初始位置． 在heff_U位置处，由于上落体P1在自由下落过程中所受到的重力梯度影响的综合效应为0，则测量得到的重力加速度值所对应的高度为
(2) 对于下落体P2，同样有
(3) ![]()
图 1 重力梯度测量算法原理Figure 1. Principle for the algorithm of the gravity vertical gradient measurement在计算重力垂直梯度时，首先计算heff_U和heff_D，然后将式(2)和(3)代入式(1)求得最终测点的垂直向重力梯度值． 对于heff_U和heff_D，二者采用的推导过程相同，这里仅以heff_U为例进行说明：
1)设定初始条件． 考虑到重力垂直梯度的测量精度要求，在heff_U的计算过程中，其计算精度须精确到mm； 对于上落体P1，从初始位置A00到位置A0的下落运动过程为非自由下落运动，距离一般小于5 μm，时间小于30 ms． 这段非自由下落运动过程对heff_U值的影响在误差允许范围内，因此在计算中可被忽略． 也就是说，假设上落体在t00时刻从初始位置A00开始进入自由下落运动，则t0=0，v0=0，x0=0； 初始位置A00的绝对重力加速度g0为已知设定值． 此外，(t1，x1)和(tn，xn)已根据所获取的干涉信号解算得到．
2) 落体的自由下落运动方程为
(4) 根据假设的初始条件，解上述方程，可得
(5) 由于gU是t1—tn时段内重力场平均作用于上落体P1的结果，则其表达式为
(6) 将式(5)代入式(6)，得
(7) 又由于gU为某个位置的绝对重力加速度值，将与其对应的位置记为C，则初始位置A00到位置C的距离记为heff_U，则
(8) 对比式(7)与式(8)，可得到
(9) 由式(9)可知，在利用同一套落体伺服控制系统对上、 下落体进行同步控制的过程中，heff_U与heff_D在对应的开始时间t1和结束时间tn的取值完全相同，即heff_U=heff_D，故将式(2)和式(3)代入式(1)，得
(10) 即利用式(1)进行重力垂直梯度计算时与g0的选取无关，仅取决于上、 下落体自由下落时重力加速度的计算和结构设计时所确定的两个落体光心之间的距离． 结构设计过程中，设上、 下落体光心间的水平距离为95 mm，若水平梯度按300—500 E(朱英，李卢玲，1982)计算，梯度测量误差为3—5 E，而本套梯度测量系统精度为100 E，因此水平梯度引入的误差可以暂时忽略，故式(1)中上、 下落体的光心间距即为上、 下落体光心间的垂直距离．
1.2 光路设计
激光干涉法重力垂直梯度测量系统的光路设计如图 2所示． 可以看到，激光器发出激光束入射至分光镜BS1的上表面，分别得到BS1上表面透射和反射两束同源激光，透射光入射至分光镜BS2的上表面，反射光经反射镜M反射后入射至分光镜BS3上表面． 分光镜BS2、 下落体P2和参考镜MS2等构成下落体P2的干涉测量光路，所形成的干涉条纹利用雪崩光电二极管(advanced photo diodes，简写为APD，下文分别用APD1和APD2表示上落体P1和下落体P2自由下落时形成的干涉条纹的接收器)接收并转换为电压信号被后端的高速数字化仪接收； 分光镜BS3、 上落体P1和参考镜MS1等构成P1的干涉测量光路，形成的干涉条纹被APD1接收并转换为电压信号被后端的高速数字化仪接收(吴琼等，2011)．
![]()
图 2 干涉法重力梯度测量原理Figure 2. Measuring principle of the gravity vertical gradient based on interferometry这套装置中，激光器、 分光镜(BS1，BS2，BS3)、 反射镜(M)、 参考镜(M1，M2)和光电接收器(APD1，APD2)均为刚性连接，真空舱中的P1和P2在同一套伺服电机控制系统作用下作自由下落运动，因此APD1和APD2接收到的干涉条纹所受到的地震动、 真空度、 气压、 极移和潮汐等环境干扰均保持相同． 源自这些因素的误差在测点重力梯度的差分计算时将被自动消除，不会影响最终测量结果的精度．
2. 测量系统设计
2.1 双落体伺服控制系统结构设计
基于激光干涉法的重力垂直梯度测量系统是利用一套电机伺服控制系统控制垂直方向间距为50 cm的两个落体作同步自由下落运动，故需要构建一个如图 3所示的真空系统，为落体的自由下落提供高真空环境，并为双落体伺服控制系统提供机械支撑．
真空系统安装在由3个支撑腿支撑的角架上，其中心旋转轴通过角架的质心，以确保角架完成水平调节后，真空系统的中心旋转轴为竖直状态． 该系统由上盖、 上二通底座、 上真空舱、 下真空舱和下二通底座等构成． 由于真空系统腔体较大，在构建真空环境时将分子泵直接安装在下二通底座上，并将其预抽至2×10-4 Pa以上时打开离子泵阀门，维持真空腔体内真空度优于5×10-4 Pa，满足落体自由下落对真空度的要求．
图 4为图 3所示真空系统内部安装的落体伺服控制系统． 图 4a显示的是落体伺服控制系统的整体结构，电机的输出力矩通过大气侧齿轮组和过真空传动机构驱动真空侧的齿条带动双落体作上下往复运动； 齿条经齿条运动导座约束后，可确保其沿竖直方向上下运动． 上托架内放置上落体P1，齿条通过万向联轴节驱动上托架，上托架沿上导轨作上下往复运动，对于下落体P2的驱动也采用同样的控制方式． 图 4b所示结构是为保证上、 下落体驱动的同步性而进行的特殊设计，由连接板、 连接块、 连接柱以及万向联轴节等构成． 连接板通过4个螺钉与上托架底端固定，末端与连接块固定； 连接块通过螺母锁定连接柱，三者构成“7”型结构； 连接柱通过万向联轴节与下托架固定． 该设计不仅可以保证上、 下托架在电机驱动下同步运动，还可抵消安装误差和制造误差所造成的径向力作用，使整套控制机构运行平稳可靠．
![]()
图 4 落体伺服控制系统设计(a)安装在真空舱内的落体伺服控制系统设计；(b)上、 下落体间刚性连接机构设计Figure 4. Design of the free-fall body servo control mechanism(a)Design of the free-fall body servo control mechanism in vacuum chamber;(b)Design of the rigid linkage between the up and down free-fall bodies2.2 双光路干涉测量系统设计
双光路干涉测量系统首先通过两个干涉光路测量单元分别采集上落体和下落体在自由下落过程中形成的激光干涉信号，再通过对其解算和差分运算得到地表重力垂直梯度．
依据图 2所示的测量原理设计双光路干涉测量系统的机械结构，如图 5所示． 激光器采用碘稳频激光系统，波长稳定度可达10-12，为整套测量系统提供长度基准． 高速数字化仪的时间基准由外部铷原子时钟提供，铷原子时钟输出频率的稳定度可达10-11，为整套仪器提供时间基准．
![]()
图 5 双光路激光干涉测量系统机构设计Figure 5. Design of the measuring structure of dual optical path measuring system based on laser interferometry干涉条纹的处理解算方面，由于上、 下落体自由下落的时间和位移信息可追溯到时间和长度基准，所以最后通过差分获得的重力垂直梯度值就具有了大动态范围、 无需标定和无零漂等特点； 构成双光路干涉测量系统所需的各个部件均刚性安装在双光路干涉测量系统的底板上，因此振动产生的误差属于共模误差，不会对最终的梯度测量结果产生影响．
光束垂直性调节方面，与激光干涉绝对重力仪不同，双光路干涉测量系统需要对两条测量光束进行垂直性调节． 首先，利用酒精液面提供的水平面和光学自准直仪，通过调整双光路干涉测量系统底板的支撑腿，调整入射上落体P1的测量光束的垂直性； 然后，同样利用酒精液面提供的水平面和光学自准直仪，通过调整反射镜M上的微调螺母，调整入射下落体P2的测量光束的垂直性． 这种调整方案的误差与光学自准直仪的误差相同，可以保证入射落体P1和P2的测量光束的垂直性误差小于0.2″．
2.3 测量系统构建与初步试验
目前，根据2.1和2.2节的设计已构建完成了一套可以正常工作的激光干涉法地表重力垂直梯度测量系统，如图 6a所示． 由于这套测量系统机构比较庞大，目前仅在实验室获取了初步的试验数据，如图 6b所示． 试验数据共有35组，每组进行16次测量.
![]()
图 6 激光干涉法地表重力垂直梯度测量系统(a)及其初步试验数据(b)Figure 6. The apparatus of the gravity vertical gradient measurement based on laser interferometry(a) and its preliminary test data(35 groups and 16 measurements per group)(b)在落体自由下落过程中，选取0.045—0.130 s时段的干涉信号进行计算． 对应落体自由下落距离为1—8 cm，生成的干涉信号是调频正弦波，频率为1.4—4.0 MHz(吴琼等，2012)． 考虑到采样频率引入的时间测量误差，选取采样频率为100 MHz，使得由采样引入的时间误差导致最终的测量误差小于1×10-8 m/s2．
图 7给出了单次测量中上落体自由下落时生成的干涉信号及其展开，可以看出，获取的干涉信号无明显干扰信号，信噪比高，可以满足高精度重力加速度值计算的要求．
![]()
图 7 实测上落体自由下落时得到的干涉条纹(a)及其展开(b)Figure 7. The interference fringes of the upper free-fall body during freely falling(a) and the expansion of the part of these fringes(b)3. 讨论与结论
在重力垂直梯度的测量过程中，潮汐、 极移、 气压、 真空度、 温度梯度、 涡流以及参考棱镜的振动等相较于明显的误差源，在绝对重力测量时不会影响重力垂直梯度的测量结果，但双落体自由下落的同步性控制、 参考点以及各个光学部件间的刚性和双测量光路的垂直性等则是影响其测量精度的重要因素．
2012年至今，在原有设计研发激光干涉重力仪的基础上，初步完成了激光干涉法地表重力垂直梯度测量系统的原理研究、 结构设计和系统构建等，并获取了本套测量系统的第一批试验数据． 从图 7所示的干涉信号可以看出，本套测量系统获取的上、 下落体在自由下落过程中所产生的干涉信号的信噪比高，干涉条纹清晰完整、 无畸变，完全满足后期的计算要求． 图 6b显示的是本次试验完成的35组测量结果的组平均值，试验中每组设定的测量次数为16次，共完成560次测量． 对测量获得的35组平均值再进行求平均计算，确定本次试验样机测量的测点的垂直向重力梯度为2886 E，精度为99 E．
2012年11月曾利用两台拉科斯特相对重力仪对本次试验所在测点的重力垂直梯度进行测量，得到的梯度值为2402 E(精度100 E)，对比分析初步确定本套梯度测量系统的测量准确度约为400 E．
本套梯度测量系统的精度和准确度不仅需要更多试验数据的测定，还需要制定更完备的测试精度和准确度的试验方案． 另外，针对伺服控制系统运行过程中的降噪问题、 数据处理算法和整套仪器的小型化设计等方面尚需进一步改进．
-
![]()
图 1 对数正态分布模型、 正态分布模型和BPT模型的概率密度
Figure 1. Probability density of lognormal distribution，normal distribution and BPT models
![]()
图 2 不含时间模型和3种含时间模型的50年内地震发生的条件概率
Figure 2. Conditional probability of earthquake occurrence in 50 years by time-independent model and the three time-dependent models
![]()
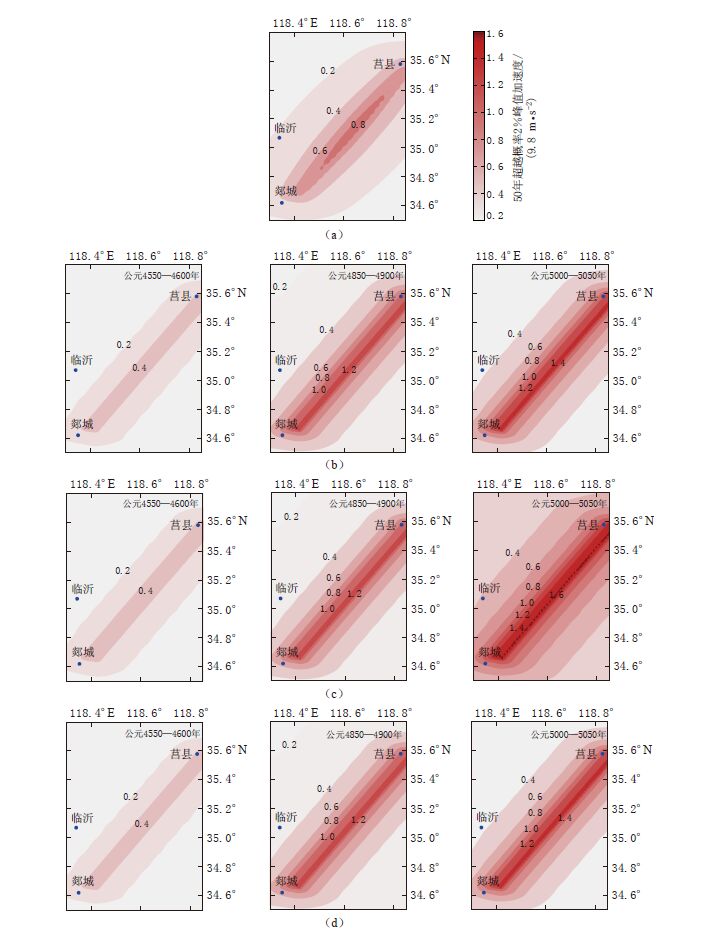
图 3 不同模型计算的郯庐断裂带莒县—郯城段及其附近地区的50年超越概率2%峰值加速度的地震危险性 (a)不含时间模型；(b)对数正态分布模型；(c)正态分布模型；(d)BPT模型
Figure 3. Seismic hazards of PGA of 2% exceedance probability in 50 years in Juxian-Tancheng segment of Tancheng-Lujiang fault and its adjacent areas calculated by different models (a)Time-independent model；(b)Lognormal distribution model；(c)Normal distribution model；(d)BPT model
![]()
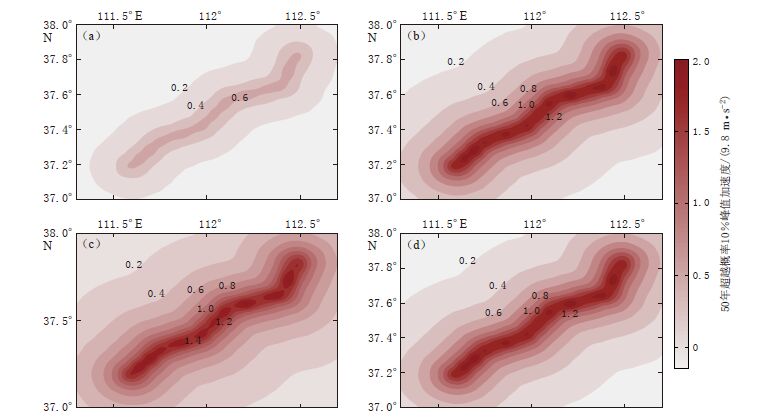
图 4 不同模型计算的交城断裂及其附近地区2015—2065年的50年超越概率10%峰值加速度的地震危险性 (a)不含时间模型；(b)对数正态分布模型；(c)正态分布模型；(d)BPT模型
Figure 4. Seismic hazards of PGA of 10% exceedance probability in 50 years from the year 2015 to 2065 in Jiaocheng fault and its adjacent areas calculated by different models (a)Time-independent model;(b)Lognormal distribution model;(c)Normal distribution model;(d)BPT model
表 1 对数正态分布模型、 正态分布模型和BPT模型在各计算时段的地震年发生率
Table 1 Annual earthquake occurrence rates in each time interval by lognormal distribution，normal distribution and BPT models
计算时段 地震年发生率 对数正态分布模型 正态分布模型 BPT模型 公元4550—4600年 0.0197 0.0322 0.0197 公元4850—4900年 0.0217 0.0497 0.0218 公元5000—5050年 0.0225 0.0608 0.0227 
下载: 导出CSV
表 2 地震动衰减关系系数(引自Sadigh et al，1997)
Table 2 Coefficients of ground motion attenuation relationship(after Sadigh et al，1997)
系数 C1 C2 C3 C4 C5 C6 C7 取值 -1.274 1.1 0.0 2.1 -0.48451 0.524 0.0
下载: 导出CSV
表 3 对数正态分布模型、 正态分布模型和BPT模型在公元2015—2065年的地震年发生率
Table 3 Annual earthquake occurrence rates by lognormal distribution，normal distribution and BPT models from the year 2015 to 2065
模型 对数正态分布 正态分布 BPT 不含时间 地震年发生率 0.0782 0.1010 0.0780 0.000395
下载: 导出CSV
-
Boyd O S, Zeng Y, Bufe C G. 2008. Toward a time-dependent probabilistic seismic hazard analysis for Alaska[G]//Active Tectonics and Seismic Potential of Alaska, Geophysical Monograph, Vol. 179. Washington D C: AGU: 399-416.
Working Group on California Earthquake Probabilities. 1988. Probabilities of Large Earthquakes Occurring in California on the San Andreas Fault[R]. USGS Open-File Report: 88-398.
Working Group on California Earthquake Probabilities. 1990. Probabilities of Large Earthquakes in the San Francisco Bay Region, California[R]. USGS Circular: 1053.
Working Group on California Earthquake Probabilities. 1999. Earthquake Probabilities in the San Francisco Bay Region: 2000—2030: A Summary of Findings[R]. USGS Open-File Report: 99-517.
Working Group on California Earthquake Probabilities. 2003. Earthquake Probabilities in the San Francisco Bay Region: 2002—2031[R]. USGS Open-File Report: 214.
Working Group on California Earthquake Probabilities. 2008. The Uniform California Earthquake Rupture Forecast, Version 2 (UCERF2)[R]. USGS Open-File Report 2007: 1437.
计量
- 文章访问数: 783
- HTML全文浏览量: 392
- PDF下载量: 22
