Comparison of seismic wavefield simulation between the curvilinear-grid finite difference method and ray method in undulated layered medium
-
摘要: 针对处理起伏地表(或含地下不规则波阻抗界面)条件下发展起来的地震波场数值模拟算法的模拟结果与解析解(大多数情形下无法得到)无法进行对比，且其有效性和正确性难以验证的情况，本文提出了一种可以相互验证波场数值模拟结果与射线追踪数值模拟结果的正确性和有效性的佐证方法，验证了参考射线追踪法.其中，波场数值模拟中采用曲线网格DRP/opt MacCormack有限差分法，射线追踪模拟则采用分区多步三角网格最短路径算法.通过系统对比上述两种方法得到的波场快照、单炮地震记录，以及合成理论地震图的结果显示，本方法相互作证了两种方法所得结果的正确性和有效性.双层和三层起伏层状模型的对比分析结果表明，这种方法不但可以加深理解地震波在复杂介质中的传播规律，同时射线法的引入为清晰识别和标定地震波场数值模拟中各种不同震相提供了一种便捷的途径.
-
关键词:
- 分区多步三角网格最短路径法 /
- 曲线网格有限差分法 /
- 地震波传播 /
- 数值模拟 /
- 起伏层状介质
Abstract: Commonly it is not possible to verify and test the accuracy and validity of the seismic wavefield modeling method, especially when the model surface (or subsurface) is undulated. For this reason, this paper tries an alternative way to mutually verify and test the computational accuracy and the solution correctness of both the ray theory (the multistage triangular shortest-path method) and the wave-equation simulation method (the curvilinear-grid finite difference method of the DRP/opt MacCormack format) in layered isotropic medium. Through the analysis and comparison of wave field snapshot, common source gather profile and synthetic seismogram, it is not only able to verify the accuracy and correctness of each of the methods at least for kinematic features, but also to thoroughly understand the kinematic and dynamic features of the wave propagation in isotropic media. The results show that the curvilinear-grid finite difference method is able to yield the correct results even for complex isotropic media; the multistage triangular shortest-path method is capable of predicting similar kinematic features as the wave-equation simulation method does, which can be used to mutually test each other for methodology accuracy and solution correctness. In addition, with the aid of the ray tracing results, it is easy to identify the multi-phases (or multiples) in the wave field snapshot, common source point gather seismic section and synthetic seismogram predicted by the wave-equation simulation method, which is a key issue for later seismic application. -
引言
“5·12”汶川地震后，一些科研人员研究指出，汶川地震造成的区域应力场改变与调整可能会导致四川盆地地震危险性的增加（Parsons et al，2008；阮祥等，2010；Lu et al，2011；宫悦等，2013；艾依飞，张健，2019；易桂喜等，2019，2020）。事实证明，汶川地震后四川盆地内中强地震比较活跃，相继发生了一系列MS4.0—5.5地震，例如2008年10月10日自贡MS4.1地震、2009年6月30日什邡MS5.5地震、2009年11月28日彭州MS5.0地震、2010年1月31日遂宁MS5.0地震、2013年2月19日三台MS4.7地震、2014年7月29日梓潼MS4.9地震、2015年1月14日金口河MS5.0地震等。
据中国地震台网测定，2013年2月19日22时17分43.4秒四川省绵阳市三台县与盐亭县交界处发生MS4.7地震，震中位置为（31.21°N，105.20°E），震源深度约为20 km。地震造成了20多户农房受损，无人员伤亡。三台地震区为弱地震活动区，本次地震为该区有地震记录以来发生的最大地震（吕锦雄等，2016；易桂喜等，2019，2020；赵博等，2019），且震区为地震研究空白区。所以，研究本次地震的发震构造、分析其是汶川“5·12”震后应力的调制震还是新构造活动所致及震区的构造应力场等，可为该区地震危险性评估、地震灾害研究与区划及防震减灾等工作提供参考。
在地震序列重定位和主震震源机制解分析的基础上，结合断层地表行迹或区域构造背景研究地震的发震构造在国内外都得到了广泛的应用（吕坚等，2008，2011；张项，2010；刘泽民等，2015；易桂喜等，2015，2016a，2017a；李翠平等，2019）。本文拟通过地震序列重定位和主震震源机制解的分析（吕锦雄，2017），结合野外地质调查和震区地质构造特征对此次地震的发震构造及发震机理进行初步研究。
1. 研究区地质简况
三台县域地势北高南低，海拔高度约为307—672 m，地貌属川中丘陵区，属于扬子准地台西北部的川中凹陷低缓构造区，为新华夏第三沉积带的川北台凹构造体系（吕锦雄，2017），地质构造简单，主要由褶皱构造组成；出露地层主要为侏罗系、白垩系及第四系，其中第四系地层主要分布在河流两岸及沟谷低洼处；基岩主要为黄褐色、紫红色和黄色中-厚层状或薄层状砂岩或泥质砂岩以及紫红色、紫褐色和灰色薄-中层状泥岩。基岩节理较发育，节理走向无明显的优势分布方向（图1）。震中附近断层有梓潼—三台断裂、绵阳—三台—大足断裂及蒲江—三台—巴中断裂。梓潼—三台断裂由李明欣（2013）通过遥感解译提出，该断裂贯穿研究区，呈近NS向展布，长度约为75.9 km，断裂性质不明；绵阳—三台—大足断裂走向约为330°，长度约为31.6 km，断裂性质不明；蒲江—三台—巴中断裂走向约为60°，长度约为56.2 km，断裂性质不明。绵阳—三台—大足断裂及蒲江—三台—巴中断裂为区域性基底大断裂（宋鸿彪，罗志立，1995；罗志立，1998；艾依飞，张健，2019）。
![]()
图 1 研究区构造背景（引自李明欣，2013）F1：汶川—青川断裂；F2：映秀—北川断裂；F3：香水断裂；F4：二郞庙断裂；F5：古城断裂；F6：平武—青川断裂；F7：茂汶断裂；F8：黄土梁断裂；F9：龙泉山断裂；F10：永兴断裂；F11：青莲场断裂；F12：梓潼—三台断裂；F13：岷江断裂；F14：黑水断裂；F15：高生庙断裂Figure 1. The tectonic background of the studied area （after Li，2013）F1：Wenchuan-Qingchuan fault； F2：Yingxiu-Beichuan fault； F3：Xiangshui fault； F4：Erlangmiao fault； F5：Gucheng fault； F6：Pingwu-Qingchuan fault； F7：Maowen fault； F8：Huangtuliang fault； F9：Longquanshan fault； F10：Yongxing fault； F11：Qinglianchang fault； F12：Zitong-Santai fault； F13：Minjiang fault； F14：Heishui fault； F15：Gaoshengmiao fault2. 地震序列分析
2.1 地震基本参数
地震发生后，四川省区域地震台网、中国地震台网中心和哈佛大学等给出了本次地震的基本参数（表1）。
表 1 三台地震参数Table 1. The parameters of the Santai earthquake发震时刻（北京时间） 北纬/° 东经/° 深度/km MS 数据来源 年-月-日 时:分:秒 2013-02-19 22:17:41.42 31.21 105.20 29.0 5.1 四川省区域地震台网 2013-02-19 22:17:43.40 31.21 105.20 20.0 4.7 中国地震台网中心 2013-02-19 22:17:44.60 31.18 105.26 19.6 4.9 哈佛大学全球矩心矩张量解 2.2 地震序列空间分布特征
精确的地震定位能准确地反映地震序列的空间分布特征，可为判断地震成因提供帮助（易桂喜等，2015，2017b；张丽芬等，2016；祁玉萍等，2018；李翠平等，2019）。地震序列重定位选用距离震中较近的安县数字化地震台网（区域台网）提供的多个地震台站（图2）记录的地震波形资料，选择信噪比高且方位角分布较好的4个以上台站，采用四川省地震局研发的数字化地震处理软件SeisDPS的区域模型搜索法，对三台MS4.7地震的前震、主震及余震进行重定位与分析。
![]()
图 2 三台地震震中区域台站分布Figure 2. Distribution of stations in epicentral zonefor Santai earthquake地震序列重定位后EW向，NS向和垂向的定位精度分别为0.8，0.7和12 km，主震震源位置为（31.22°N，105.21°E），深度为21.6 km。地震序列震中分布如图3a所示。
![]()
图 3 三台MS4.7地震序列震中分布图Figure 3. Epicenter distribution diagram of Santai MS4.7 earthquake sequence由图3a可知，余震序列长轴沿NW-SE方向展布，长轴约为18.3 km，短轴约为11.3 km，主震NW侧余震明显多于SE侧，且较大余震主要集中在主震附近。根据余震序列的空间展布可判断三台地震的发震构造为NW-SE走向。
地震序列的震源位置和余震深度的展布可以反映主震发震断层的几何形态，也可为探索地震孕育、发生的深部环境提供依据（Wu，Takeo，2004）。地震序列震源深度沿剖面AA′和剖面BB′的分布如图3b，c所示。从地震序列深度剖面可以看出，余震的深度主要为5—25 km，分布较分散，绝大多数的余震较主震浅，说明破裂面以向上部扩展为主。剖面AA′显示主震SE侧余震数目远少于NW侧，说明NW方向为地震序列扩展的优势方向。剖面BB′反映沿断层倾向震源分布较分散。
3. 震源机制解分析
利用震源机制解分析地震的成因和了解地震发生时震源部位的应力状态及运动学特征，有助于理解发震构造条件（杜龙等，2009；罗艳等，2015；吕锦雄等，2016；易桂喜等，2016b，2017b；李翠平等，2019；李君，2019）。很多科研人员曾采用近远震联合波形反演法求解了主震震源机制（黄建平等，2009；谢祖军等，2013；郑建常等，2013；吕锦雄，2017；朱冰清等，2019）。通常近场记录由于受地壳速度结构模型的影响较小，对震源性质更敏感，反演的震源机制更准确；而远场所记录的数据包含了pP，sP，sS和pS等深度震相的信息，对于中强地震的深度约束更好。因此，利用近远场的波形数据反演得到的震源机制解参数更加可靠（吕锦雄，2017）。近震波形数据由安县地震台网提供，远震数据来自美国地震学研究联合会（Incorporated Research Institutions for Seismology，缩写为IRIS）网站，取震中距在30°—90°之间和信噪比较高的波形数据，远震台站信息列于表2。地壳速度模型采用绵阳市地震局编著的《绵阳市及邻区地震分布规律研究》（杨恒书等，2016）一书中提到的四川地区地壳结构模型（表3）。近远震联合反演的误差-深度分布及主震震源机制解见表4及图4，最佳深度约为19 km，与重定位深度接近，矩震级为MW4.88。
表 2 远震台站统计表Table 2. Statistical table of remote seismic stations台站名 方位角/° 震中距/° 纬度/° 东经/° 台站名 方位角/° 震中距/° 纬度/° 东经/° HKPS 136.36 11.94 22N 114 KIEV 313.46 57.87 51N 29 KBS 347.20 60.05 79N 12 UOSS 274.40 43.39 25N 56 PET 44.16 43.87 53N 159 DGAR 224.74 49.78 7S 72 ARU 322.04 40.87 56N 59 COCO 191.88 44.16 12S 97 TIXI 10.79 42.36 72N 129 GUMO 106.82 40.34 14N 145 表 3 地壳速度模型参数表Table 3. Table of crustal velocity model parameters名称 深度/km P波速度/(km·s−1) 名称 深度/km P波速度/(km·s−1) 第1层 5 5.86 第4层 23 5.9 第2层 14 6.00 第5层 36 6.6 第3层 21 6.30 第6层 40 7.1 表 4 三台地震主震震源机制解参数Table 4. Parameters of focal mechanism solution for the mainshock of Santai earthquake sequence节面Ⅰ 节面Ⅱ P 轴 T 轴 N 轴 来源 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° 方位/° 倾角/° 方位/° 倾角/° 方位/° 倾角/° 320 83 −175 230 85 −5 182 4 274 5 30 85 本文 316 82 −177 226 87 −8 181 7 271 3 27 82 哈佛大学 ![]()
图 4 近远震联合反演的误差-深度分布图及主震震源机制解（a） 误差-深度分布图；（b） 本文所得震源机制解；（c） 哈佛大学给出的震源机制解Figure 4. Misfit variation with focal depth using CAP joint method and focal mechanism solutions of the mainshock（a） Error-depth distribution diagram；（b） The focal mechanism solution obtained in this study； （c） The focal mechanism solution given by Harvard University从表4和图4b，c可以看出，本文得到的三台地震主震震源机制与美国哈佛大学依据全球远场波形反演的震源机制十分接近。
单次地震震源机制解的主轴与该地震释放的应力有关（Mckenzie，1969；Raleigh et al，1972；刘泽民等，2015），即只反映本次地震产生时的构造作用力。由表4及图4中的P，T轴方位角可知，震源区构造应力场的主压应力轴为近NS向，主张应力轴为近EW向，反映产生本次地震的构造作用力与秦启荣等（2005）提出的川中地区NS向挤压的区域构造应力场特征基本一致（吕锦雄，2017）；由P，T轴的仰角可知，震源区的构造应力场近于水平，与成尔林（1981）、许忠淮等（1987）、蒋良文（1999）、马文涛等（2011）、曹颖等（2012）和李君等（2019）提出的四川盆地内区域构造应力场基本一致（吕锦雄，2017）；N轴倾角很大，说明断裂水平剪切错动。震源机制解两个节面的倾角都较陡，说明此次地震的发震构造近于直立。
4. 发震构造与发震机理分析
三台地震主震震源机制解（表4、图4）中的NW-SE向节面 Ⅰ 与重定位后的余震序列空间展布长轴方向一致，且在地震序列震中分布图（图3）中沿节面 Ⅰ 即剖面AA′的走向320°看去，主震东侧的余震多于西侧，这与断层上盘余震多于下盘余震的上盘效应现象相吻合（毛玉平，万登堡，2001；俞言祥，高孟潭，2001；何仲太等，2012；吕锦雄等，2016；罗全波等，2019），从而推断主震震源机制解中的节面Ⅰ为发震断裂面，即发震断层走向为NW-SE向，倾向为NE，倾角陡直，为有微小张性分量的右旋走滑型断裂。结合节面Ⅰ倾角83°及重定位后主震震源深度21.6 km，经计算地震的发震构造从主震震中SW侧约2.65 km处通过。对该带进行野外地质调查，调查中未见地表破碎带或显著的断层迹象，且研究区的节理走向无明显的优势方向，所以认为发震断裂可能为隐伏性构造。研究区有区域性基底大断裂通过，此次地震发生于绵阳—三台—大足断裂与蒲江—三台—巴中断裂的交会处（图5）。绵阳—三台—大足断裂与蒲江—三台—巴中断裂为四川盆地内部存在的基底深断裂，它们与其它深断裂将四川盆地基底分割成众多的或大或小的菱形块体，对四川盆地不同时期的构造演化，特别是晚中生代以后的构造格局的改造与发展有着重要影响（宋鸿彪，罗志立，1995；罗志立，1998；艾依飞，张健，2019）。本次三台地震序列的余震空间分布呈NW-SE向，且震源机制解的节面Ⅰ走向为320°，与绵阳—三台—大足断裂的走向非常接近且断裂性质相似，但此断裂与震源区相隔较远，距离大于15 km，与震源区位置无明显衔接；而蒲江—三台—巴中断裂呈NE-SW走向，与此次地震余震区长轴走向不符。可见，发震构造没有明显已知构造与其对应，据此推断可能为未知隐伏构造。
![]()
图 5 三台MS4.7地震震区地震地质图Figure 5. Seismogeologic map for the seismic region of Santai MS4.7 earthquake震源深度是地震学研究的关键参数，也是目前难以准确测定的参数，精确测定震源深度有助于了解地震活动与断层之间的关系（张帆等，2017，2019）。四川盆地内发生的与逆断层伴生的背斜构造有关的中强地震，具有震级低、震源浅的特点：例如1962年洪雅MS5.1地震，震源深度为5 km；1967年仁寿MS5.5地震，震源深度为4 km；1985年自贡MS4.6地震，震源深度为5 km；1989年重庆江北MS5.4地震，震源深度为5 km，这些地震震源深度位于沉积盖层内的弱岩层滑脱面之上（钱洪等，1992；黄圣睦等，2003），且背斜和逆断层常同步消失于地下3—6 km的低强度的砂页岩和泥岩的岩石中（钱洪，1995；周荣军等，2005）；蔡学林和曹家敏等（1998）研究认为盆地内构造变形主要沿基底与盖层间滑脱面以上5—10 km的沉积岩层发育，其变形构造为薄皮构造（张维宸，2009），该薄皮构造控制了盆地内地震震源深度。钱洪和唐荣昌（1992）研究认为作用于四川盆地的微弱现代构造应力场不足以推动盆地中的基底断裂，不会发生由于基底断裂的强烈断错而诱发强烈破坏性地震。但“5·12”汶川地震后，盆地内的中强地震明显增加，且震源深度都较大，例如遂宁MS5.0地震震源深度为10 km （Lu et al，2011）；金口河MS5.0地震震源深度为12 km （马超等，2017）等。从震源深度来看作者认为这两次地震也还是发生于盆地内基底与盖层间的滑脱面上或其上部。但也有发生于盆地基底断裂中的地震：如彭州MS5.0地震震源深度为21 km （黄闻等，2010）；梓潼MS4.9地震震源深度为21 km （吕锦雄等，2016）。本研究中的三台地震震源深度重定位结果为21.6 km，震源区位于盆地内川中地块上地壳底部的低速层内（图6），川中上地壳底部有厚约6 km的低速层，可能由花岗质的糜棱岩层组成，是具有塑性的滑脱层（罗志立，1998；张维宸，2009）。从震源深度来说，本文结果与罗钧等（2014）、李君等（2019）认为的四川盆地内地震大都发生在15—30 km深度的观点相吻合。
![]()
Figure 6. Model for the crust thickness and velocity structure （Cai et al，2008，2010）. The data in parentheses is the mean of participating，and the dotted line represents the low velocity layer in the crust周缘造山带应力状态发生重大变化导致四川盆地内部构造应力场的变化与调整，使盆地盖层断层与基底断裂及其次级断裂附近应力集中，增大了盆地内发生中强地震的可能性，作者认为发生于汶川地震后，震源深度大于20 km的中强地震应为四川盆地基底断裂重新活动的反映。已有研究表明四川盆地内区域构造应力场为近NS向的近水平挤压和近EW向的近水平拉张（成尔林，1981；许忠淮等，1987；蒋良文，1999；秦启荣，2005；马文涛等，2011；曹颖等，2012；李君等，2019）。盆地内区域应力场的最大主压应力轴方位角与本次地震推测发震断裂走向夹角约为40°，而最小主压应力轴方位角与推测发震断裂的走向夹角约为50°。在此区域应力场的作用下，发震断裂的摩擦阻力较小，而张性右旋作用较大（刘泽民等，2015），从而基底断裂发生张性右旋走滑错动，此结果与主震的震源机制解亦吻合较好（图7）。
![]()
图 7 构造应力场和震源机制解示意图Figure 7. Sketch map of tectonic stress field and focal mechanism solution5. 讨论与结论
汶川地震后，四川盆地内中强地震活动变得活跃。三台地震震级较小，无法得到有明显方向性的地震动衰减等震线图。利用地震目录、震相报告和波形等相关资料对三台地震的地震序列、主震震源机制解及发震构造等方面进行研究，并初步分析其发震机理，获得如下认识：
1） 根据主震震源机制解及地震序列重定位结果，该地震是发生在四川盆地内的一次有微小张性分量的右旋走滑破裂事件；
2） 发震构造无明显已知构造与其对应，可能为未知隐伏构造，发震断裂走向为NW-SE，倾向为NE，倾角近于直立；
3） 三台地震是在四川盆地近NS向的近水平挤压和近EW向的近水平拉张作用的区域构造应力场作用下，汶川地震造成的区域构造应力场改变与调整过程中，隐伏于前震旦纪结晶基底中的高角度断裂重新活动的结果。在区域构造应力作用下，活动断裂在四川盆地川中地块内的上地壳底部低速层活动，从而引发具有微小张性分量的走滑型地震事件。
绵阳市防震减灾局、安县防震减灾局及三台县防震减灾办公室在资料收集及野外工作中给予了大力支持，四川省地震台网、安县地震台站提供了地震资料及相关软件，作者在此一并表示感谢。
-
![]()
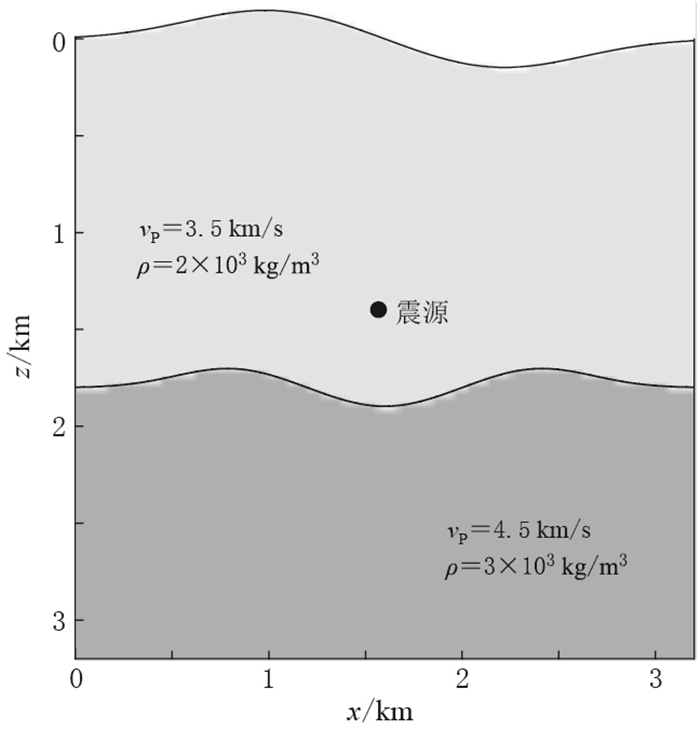
图 1 含起伏界面的层状模型示意图
(a)计算反射波、透射波、转换波的模型示意图；(b)模型参数化时所采用的三角单元十字表示震源；圆圈表示主节点；圆点表示次级节点
Figure 1. Schematic diagram of the undulating layered medium model
(a) A schematic explanation for computing the transmitted, reflected and converted arrivals; (b) A triangular cell used in the model parameterization The cross indicates earthquake source, circles indicate primary nodes, and dots indicate secondary nodes
![]()
图 2 起伏层状均匀介质中多震相射线路径
(a)一次纯P波反射波；(b)一次纯S波反射波；(c)一次P-S波反射转换波；(d)一次S-P波反射转换波
Figure 2. The multi-phase ray paths of undulating layered medium
(a) Purely primary reflected P-wave; (b) Purely primary reflected S-wave; (c) Primary reflected and converted from P to S wave; (d) Primary reflected and converted from S to P wave
![]()
图 3 曲线网格和计算网格的网格变换关系
Figure 3. Mapping between the boundary-conforming grid and uniform grid
![]()
图 5 双层介质模型中t=0.6 s时x分量波场快照.虚线表示模型速度界面
(a)曲线网格DRP/opt MacCormack差分法模拟结果；(b) MTSPM射线追踪法结果
Figure 5. Snapshots of x component wave field at the moment of 0.6 s for the two-layer model where the dashed lines indicate the model subsurface
(a) Results by the curvilinear-grid finite difference method of the DRP/opt MacCormack; (b) Results by MTSPM ray tracking algorithm ① P1; ② S1; ③ P1P1; ④ P1S1; ⑤ S1P1; ⑥ S1S2; ⑦ P1S2; ⑧ S1P2; ⑨ P1P2; ⑩ S1S1; ⑪ P1S1; ⑫ P1P1
![]()
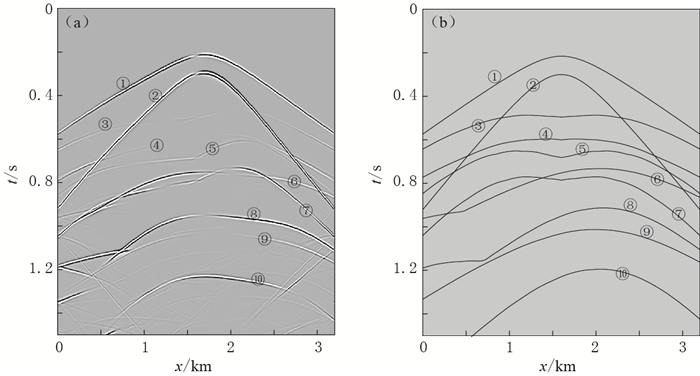
图 6 双层模型中x分量单炮地震记录剖面
(a)曲线网格DRP/opt MacCormack差分法模拟结果; (b) MTSPM射线追踪法结果
Figure 6. Common source point gather of x component for two-layer model
(a) Results by the curvilinear-grid finite difference method of the DRP/opt MacCormack; (b) Results by MTSPM ray tracking algorithm ① P1; ② S1; ③ P1P1; ④ S1P1; ⑤ P1S1; ⑥ P1P1; ⑦ S1S1; ⑧ P1S1; ⑨ S1P1; ⑩ S1S1
![]()
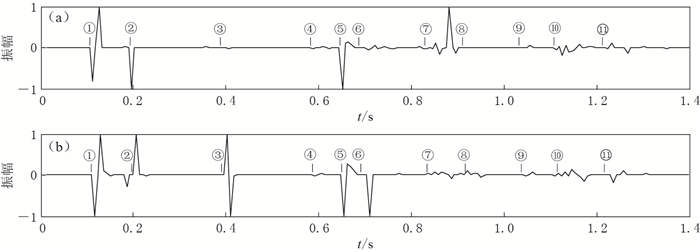
图 7 基于曲线网格DRP/opt MacCormack差分法得到的双层介质模型中x分量(a)和z分量(b)的合成理论地震图
垂线为MTSPM算法所预测的各震相理论初至时间
Figure 7. Synthetic seismogram for two-layer model with the curvilinear-grid finite difference method of the the DRP/opt MacCormack for x component (a) and z component (b)
Vertical lines indicate the onset times for possible phases by MTSPM algorithm. ① P1; ② S1; ③ P1P1; ④ S1P1; ⑤ P1P1; ⑥ S1S1; ⑦ P1S1; ⑧ S1P1; ⑨ P1P1P1; ⑩ S1S1; ⑪ P1P1P1
![]()
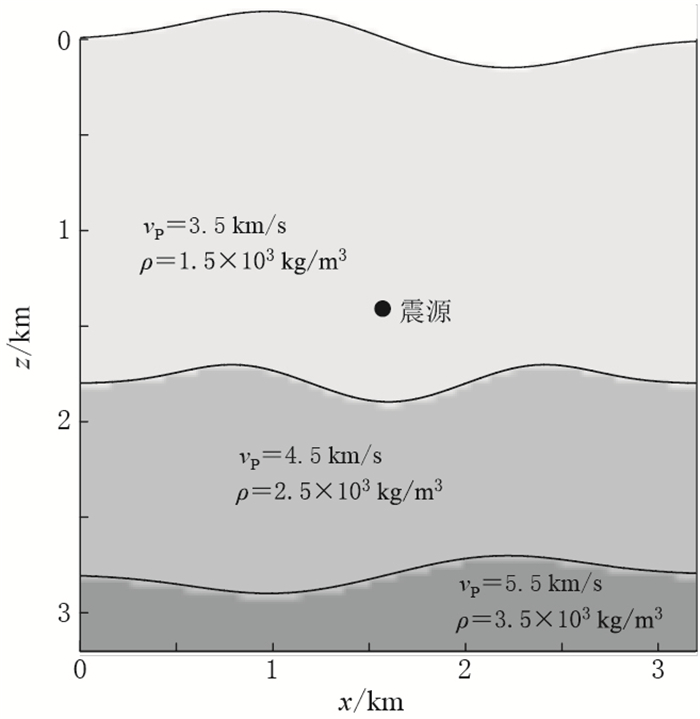
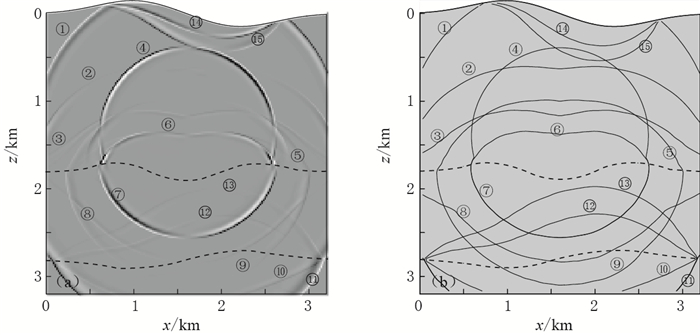
图 9 三层均匀介质模型中t=0.6 s时x分量波场快照.虚线表示模型速度界面
(a)曲线网格DRP/opt MacCormack差分法模拟结果; (b) MTSPM射线追踪法结果
Figure 9. Snapshots of x component wavefield at the moment of 0.6 s for the three-layer model where the dashed lines indicate the model subsurface
(a) Results by the curvilinear-grid finite difference method of the DRP/opt MacCormack; (b) Results by MTSPM ray tracking algorithm ① P1; ② P1P1; ③ P1S1; ④ S1; ⑤ S1P1; ⑥ S1S1; ⑦ S1S2; ⑧ S1P2; ⑨ P1S2; ⑩ P2P2S3; ⑪ P1P2P3; ⑫P1P2P2; ⑬ P1P2S2; ⑭ P1P1; ⑮ P1S1
![]()
图 10 三层模型中x分量单炮地震记录剖面
(a)曲线网格DRP/opt MacCormack差分法模拟结果；(b) MTSPM射线追踪法结果
Figure 10. Common source point gather of x component for three-layer model
(a) Results by the curvilinear-grid finite difference method of the DRP/opt MacCormack; (b) Results for MTSPM ray tracking algorithm ① P1; ② S1; ③ P1P1; ④ S1P1; ⑤ P1S1; ⑥ P1P1; ⑦ S1S1; ⑧ P1P2P2P1; ⑨ P1S1; ⑩ P1S2P2P1; ⑪ S1P1; ⑫ P1P2P2S1
![]()
图 11 基于曲线网格DRP/opt MacCormack差分法得到的三层介质模型中x分量(a)和z分量(b)的合成理论地震图
垂线为MTSPM算法各震相的理论初至时间
Figure 11. Synthetic seismogram for three-layer model with the curvilinear-grid finite difference method of the DRP/opt MacCormack for x component (a) and z component (b)
Vertical lines indicate the onset times for possible phases by MTSPM algorithm. ① P1; ② S1; ③ P1P1; ④ S1P1; ⑤ P1S1; ⑥ P1P1; ⑦ S1S1; ⑧ P1P2P2P1; ⑨ P1S1; ⑩ P1P2S2P1; ⑪ S1P1; ⑫ P1P2P2S1; ⑬ P1P2S2S1; ⑭ P1S2S2S1; ⑮ S1S2S2S1
-
黄国娇. 2014.各向同性/各向异性介质中多震相走时同时反演方法技术研究[D].西安:长安大学地质工程与测绘学院: 16-19. http://cdmd.cnki.com.cn/Article/CDMD-10710-1014070093.htm Huang G J. 2014. Simultaneous Traveltime Inversion in Complex Isotropic/Anisotropic Medium Using Multi-Phase Arrivals[D]. Xi'an: College of Geological Engineering and Surveying, Chang'an University: 16-19 (in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10710-1014070093.htm
黄国娇, 白超英, 钱卫. 2015.球坐标系下多震相走时三参数同时反演成像[J].地球物理学报, 58 (10): 3627-3638. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201510016.htm Huang G J, Bai C Y, Qian W. 2015. Simultaneous inversion of three model parameters with multiple phases of arrival times in spherical coordinates[J]. Chinese Journal of Geophysics, 58 (10): 3627-3638 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201510016.htm
蒋丽丽, 孙建国. 2008.基于Poisson方程的曲网格生成技术[J].世界地质, 27 (3): 298-305. http://www.cnki.com.cn/Article/CJFDTOTAL-SJDZ200803012.htm Jiang L L, Sun J G. 2008. Source terms of elliptic system in grid generation[J]. Global Geology, 27 (3): 298-305 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-SJDZ200803012.htm
李晓玲, 白超英, 胡光义. 2013.起伏层状TI介质中多次波射线追踪[J].石油地球物理勘探, 48 (6): 924-931. http://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ201306011.htm Li X L, Bai C Y, Hu G Y. 2013. Multiple ray tracing in an undulated layered TI media[J]. Oil Geophysical Prospect-ing, 48 (6): 924-931 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ201306011.htm
王涛, 张延腾, 白超英. 2014. 2D各向异性TTI介质中地震波场的射线法和波动方程数值模拟对比研究[J].地球物理学进展, 29 (2): 580-587. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201402014.htm Wang T, Zhang Y T, Bai C Y. 2014. Seismic wavefield propagation on 2D anisotropic TTI media through ray theory and wave-equation simulation and comparison[J]. Progress in Geophysics, 29 (2): 580-587 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201402014.htm
王涛, 白超英, 杨尚倍. 2016.各向同性介质中射线理论与有限差分地震波场模拟方法比较研究[J].地球物理学进展, 31 (2): 606-613. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201602013.htm Wang T, Bai C Y, Yang S B. 2016. Comparison of ray theory and FDM for simulating seismic wavefield in isotropic media[J]. Progress in Geophysics, 31 (2): 606-613 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201602013.htm
王童奎, 张美根, 李小凡, 李瑞华, 龙桂华. 2007. PS转换波界面二次源法射线追踪[J].地球物理学进展, 22 (1): 165-170. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ200701022.htm Wang T K, Zhang M G, Li X F, Li R H, Long G H. 2007. Interface points as secondary sources method raytracing PS converted waves[J]. Progress in Geophysics, 22 (1): 165-170 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ200701022.htm
赵爱华, 张中杰. 2004.三维复杂介质中转换波走时快速计算[J].地球物理学报, 47 (4): 702-707. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200404023.htm Zhao A H, Zhang Z J. 2004. Fast calculation of converted wave traveltime in 3-D complex media[J]. Chinese Journal of Geophysics, 47 (4): 702-707 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200404023.htm
赵爱华, 丁志峰. 2005.宽角反射地震波走时模拟的双重网格法[J].地球物理学报, 48 (5): 1141-1147. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200505022.htm Zhao A H, Ding Z F. 2005. A double-grid algorithm for calculating traveltimes of wide-angle reflection waves[J]. Chinese Journal of Geophysics, 48 (5): 1141-1147 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200505022.htm
朱多林, 白超英. 2011.基于波动方程理论的地震波场数值模拟方法综述[J].地球物理学进展, 26 (5): 1588-1599. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200505022.htm Zhu D L, Bai C Y. 2011. Review on the seismic wavefield forward modelling[J]. Progress in Geophysics, 26 (5): 1588-1599 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200505022.htm
Bai C Y, Li X L, Wang Q L, Peng J B. 2012. Multiple arrival tracking within irregular triangular or tetrahedral cell model[J]. J Geophys Eng, 9 (1): 29-38. doi: 10.1088/1742-2132/9/1/004
Carcione J M, Herman G C, Kroode A P E. 2002. Seismic modeling[J]. Geophysics, 67 (4): 1304-1325. doi: 10.1190/1.1500393
Červený V. 2001. Seismic Ray Theory[M]. Cambridge: Cambridge University Press: 117-118.
Crampin S. 1984. Effective anisotropic elastic constants for wave propagation through cracked solids[J]. Geophys J Int, 76 (1): 135-145. doi: 10.1111/j.1365-246X.1984.tb05029.x
Hixon R. 1998. Evaluation of a high-accuracy MacCormack-type scheme using benchmark problems[J]. J Comp Acoust, 6 (3): 291-305. doi: 10.1142/S0218396X9800020X
Hixon R, Turkel E. 2000. Compact implicit MacCormack-type schemes with high accuracy[J]. J Comp Phys, 158 (1): 51-70. doi: 10.1006/jcph.1999.6406
Igel H, Mora P, Riollet B. 1995. Anisotropic wave propagation through finite-difference grids[J]. Geophysics, 60 (4): 1203-1216. doi: 10.1190/1.1443849
Komatitsch D, Barnes C, Tromp J. 2000. Simulation of anisotropic wave propagation based upon a spectral element method[J]. Geophysics, 65 (4): 1251-1260. doi: 10.1190/1.1444816
Moser T J. 1991. Shortest path calculation of seismic rays[J]. Geophysics, 56 (1): 59-67. doi: 10.1190/1.1442958
Tam C K W, Webb J C. 1993. Dispersion-relation-preserving finite difference schemes for computational acoustics[J]. J Comp Phys, 107 (2): 262-281. doi: 10.1006/jcph.1993.1142
Zhang W, Chen X F. 2006. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J]. Geophys J Int, 167 (1): 337-353. doi: 10.1111/gji.2006.167.issue-1
Zhang W, Zhang Z G, Chen X F. 2012. Three-dimensional elastic wave numerical modelling in the presence of surface topography by a collocated-grid finite-difference method on curvilinear grids[J]. Geophys J Int, 190 (1): 358-378. doi: 10.1111/gji.2012.190.issue-1
Zhou H, Chen X F. 2008. Localized boundary integral equation-discrete wave number method for simulating wave propagation in irregular multiple layers, part I: Theory[J]. Bull Seismol Soc Am, 99 (3): 1984-1994.
Zhu J L, Dorman J. 2000. Two-dimensional, three-component wave propagation in a transversely isotropic medium with arbitrary orientation-finite-element modeling[J]. Geophysics, 65 (3): 934-942. doi: 10.1190/1.1444789
-
期刊类型引用(1)
1. 丁志华，崔月菊，盛艳蕊，张子广. 高光谱气体背景场特征及震情跟踪应用前景. 华北地震科学. 2019(03): 44-49 . 
百度学术
其他类型引用(5)
下载:
计量
- 文章访问数: 672
- HTML全文浏览量: 271
- PDF下载量: 21
- 被引次数: 6
