Quantitative analysis and discrimination of groundwater type in well-aquifer system
-
摘要: 利用水位、 气压和理论固体潮数据, 采用卷积回归法中水位对气压的阶跃响应函数, 定量地分析和判定了华北北部板桥井、 大灰厂井、 黄骅井、 大甸子井、 丰镇井和三号地井的井-含水层系统的地下水类型, 并结合研究时段内各井的气压系数和M2波潮汐因子的结果进行了对比分析. 结果表明: ① 各井的滞后时间与阶跃响应函数之间存在明显的以e为底的指数函数关系, 且底数e的系数的正负决定了井-含水层系统的地下水类型; ② 承压井的阶跃响应函数随滞后时间的增大而增大, 且最佳阶跃响应函数值越大, 相应的气压系数和M2波潮汐因子也越大, 反之亦然; ③ 潜水井和半承压水井的阶跃响应函数随滞后时间的增大而减小, 其最佳阶跃响应函数与气压系数和M2波潮汐因子间的关系不明显, 可能与含水层的水力特性、 井孔结构及固体潮汐波的频率有关.Abstract: In this study, we quantitatively analyzed and determined groundwater types of well-aquifer system for the wells Banqiao, Dahuichang, Huanghua, Dadianzi, Fengzhen and Sanhaodi by using water level, barometric pressure and theoretical earth tide. Furthermore, combining with step response function of water level to barometric pressure in convolutional regression, barometric coefficient and tidal factor of M2 wave are comparatively analyzed for each well in the studied period. The results show that: ① an obvious exponential relationship exists between lag time and step response function with “e” as the bottom, and the sign symbol of the coefficient before the base “e” could determine groundwater types of well-aquifer system; ② step response function is growing with lag time increase for artesian wells, and the larger the optimal step response function value is, the larger barometric coefficient and tidal factor of M2 wave are, and the reverse is also true; ③ step response function decreases with latency increase for phreatic and half artesian wells, and because of hydraulic characteristics of aquifer, borehole structures and frequency of solid tidal waves, the relationship between the optimal step response function and barometric coefficient, tidal factor of M2 wave is inconspicuous.
-
引言
根据地下水的储存埋藏条件,可将其分为包气带水、 潜水和承压水等3种主要类型(王大纯等,1995),其中具有承压性的井-含水层系统具备进行地震地下水前兆观测的理想条件. 但对于地震观测而言,观测井还需避开浅层地下水干扰. 例如深层承压水,要求观测井不但具有承压性,而且应具有一定深度的隔水层等,以减少可能出现的应力应变干扰. 目前应用于地震前兆观测的井孔,其地下水类型主要为潜水、 承压水以及二者的混合型(混合水或半承压水). 多年来,水文地质工作人员已从主要种类、 成因、 补给区与分布区的关系和动态特征等方面定性地分析了潜水和承压水等的分类原则、 分类标准和主要特征(秦同洛等,1989;国家地震局科技监测司,1995;王大纯等,1995).
考虑水位与气压间的非线性关系及滞后时间的卷积回归法,已成为近年来气压校正的主要方法之一(Rasmussen,Crawford,1997;Toll,Rasmussen,2007;Darner,Sheets,2012;方慧娜,2013;Husseinet al,2013;史浙明,王广才,2013;赵丹,王广才,2013;杨柳等,2014).该方法通过引入井水位对气压的阶跃响应函数,利用相应的水位和气压数据拟合出阶跃响应函数的最佳值,再由该最佳阶跃响应函数对水位进行校正. 若将固体潮因素(一般由传感器测量值或理论固体潮代替)考虑在内,该方法可同时校正观测井水位数据中的气压和固体潮.
在利用卷积回归法进行水位的气压和固体潮校正方面已经有了大量的研究成果,但在利用井水位对气压的阶跃响应函数进行地下水类型的定量判别方面的研究鲜有报道.Rasmussen和Crawford(1997)曾指出井水位对气压的滞后时间与阶跃响应函数之间存在以自然数e为底的指数函数关系,但其研究仅针对非承压(潜水)和半承压状态而言. 承压井含水层系统是否存在这样的指数关系,以及与非承压和半承压井相比,不同地下水类型具有的指数关系的差异性仍不明确,因此有必要深入开展利用井水位对气压的阶跃响应函数对地下水类型进行定量的研究,这对地震地下流体前兆观测测点的堪选,以及观测资料质量和可信度等的甄别均具有重要意义.
鉴于此,本文拟利用板桥、 大灰厂、 黄骅、 大甸子、 丰镇和三号地等6口井的水位、 气压和理论固体潮数据,结合卷积回归法中水位对气压的阶跃响应函数,定量地分析和判定各井的井-含水层系统的地下水类型,并结合研究时段内各井的气压系数和M2波潮汐因子进行对比分析,以期综合判定和检验井-含水层系统的地下水类型.
1. 基本理论及数据预处理
1.1 井水位对气压的阶跃响应函数
依据前人的研究结果(Rasmussen,Crawford,1997;Toll,Rasmussen,2007;王丽亚等,2012;李悦等,2015),采用卷积回归法,利用各井的水位、 气压和理论固体潮数据拟合最佳阶跃响应函数,并判断响应的滞后时间,最终计算出校正后的水位.
在不考虑补给和排泄等因素的情况下,井水位的变化量可表示为

(1) 式中,i为滞后时间,m为设置的最大滞后时间,ΔW(t)为t时刻的水位变化量,α(i)为滞后i时刻的气压单位脉冲响应函数,ΔB(t-i)为t-i时刻的气压变化量,β(i)为固体潮响应系数,ΔE(t-i)为t-i时刻的固体潮变化量.
井水位对气压的阶跃响应函数A(i)可表示为

(2) 校正后的水位可表示为

(3) 式中,Wt*为m-n时间内每个水位观测值的校正量,m为设置的最大滞后时间,n为观测数据个数,αm为与最大滞后时间对应的气压单位脉冲响应函数.
1.2 气压系数的获取
假设将水位的影响因素分解为气压、 潮汐、 趋势成分和随机成分等4个因素. 首先用卷积回归法剔除潮汐成分,然后用一般多项式分段拟合去除趋势和随机成分直至水位只余气压效应项. 若气压数据的趋势明显则要事先进行线性去趋势. 最后,利用剩余水位(只剩气压效应项的水位)和校正后的气压采用一阶差分来获取气压系数.
1.3 M2波潮汐因子的获取
利用卷积回归法剔除井水位的气压成分(气压校正),再用一般多项式分段拟合去除趋势和随机成分直至水位只余潮汐响应(固体潮效应)项,最后利用维尼迪柯夫调和分析程序获得M2波的潮汐因子等参数.
1.4 数据整理和预处理
首先,将数字化观测的板桥井、 大灰厂井、 黄骅井、 大甸子井、 丰镇井和三号地井等6口井的水位和气压分钟值数据转换为整点值,并结合三次样条插值和一般多项式分段拟合值进行缺数补齐; 其次,整理各井点的理论固体潮整点值; 最后,准备各井点的excel文件,内容包括时间(等间隔的整点值)、 水位、 气压和理论固体潮. 需要说明的是: 水位须由埋深值换算成水头高度值,单位为m.
2. 井水位对气压的阶跃响应函数及其变化特征
2.1 水井参数
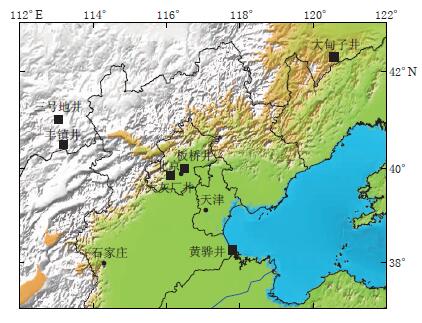
本文研究的板桥井、 大灰厂井、 黄骅井、 大甸子井、 丰镇井和三号地井等6口井主要位于华北北部,如图 1所示. 各井的井深、 含水层岩性、 地下水类型(依据贮存埋藏条件定性判定)、 水位埋深以及资料分析研究的起止时间等参数列于表 1.
表 1 本研究使用的6口井的基本参数Table 1. General information of six wells used in this study井点名称 井深/m 含水层岩性 地下水类型* 水位埋深/m 资料选取时段 板桥 283.60 硅质石灰岩 裂隙承压水 39.60 2011-01—2011-12 大灰厂 102.00 砂页岩 孔隙裂隙混合水 14.50 2011-01—2011-12 黄骅 1250.00 灰岩 裂隙承压水 5.20 2007-01—2007-12 大甸子 200.76 砂岩、 砂板岩 裂隙承压水 18.80 2002-01—2002-12 丰镇 98.99 砂砾岩 承压水 2.36 2014-06—2015-05 三号地 100.00 玄武岩 孔隙裂隙潜水 51.20 2013-01—2013-12 * 地下水类型依据储存埋藏条件定性判别而得. 2.2 滞后时间与阶跃响应函数之间的关系
本文在研究滞后时间与阶跃响应函数之间的关系时,同时进行气压和固体潮校正,参考Toll和Rasmussen(2007)将水位对气压的最大滞后时间也设为12 h,以便对计算结果进行比较,验证其可靠性.
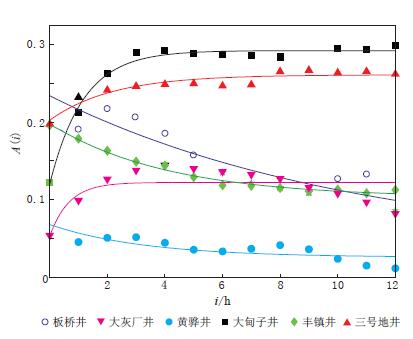
图 2给出了6口井的水位对气压的阶跃响应函数与滞后时间的关系曲线,其具体的统计关系及参数设置列于表 2. 从图 2和表 2可以看出,水位对气压的阶跃响应函数与滞后时间之间存在明显的以e为底的指数函数关系.通过对指数曲线的分析可知: 其滞后时间i的取值范围为0—12 h,阶跃响应函数A(i)的值域为0—1; 随着水位对气压的滞后时间逐渐增大,板桥井、 黄骅井和丰镇井的水位对气压的阶跃响应函数呈递减形式,这表明当底数e的系数大于0时,阶跃响应函数随滞后时间的增大而减小,井-含水层系统地下水类型为潜水或半承压水; 随着滞后时间逐渐增大,大灰厂井、 大甸子井和三号地井的阶跃响应函数呈增大趋势,这表明当底数e的系数小于0时,阶跃响应函数随滞后时间的增大而增大,井-含水层系统的地下水类型为承压水. 由此推断,底数e的系数的正负决定了井-含水层系统的地下水类型; 各井滞后时间i的系数均小于零,其值与井-含水层系统的地下水类型并无明显相关性,而与井孔的形状、 尺寸(结构)和含水层的水力特性有关(Rasmussen,Crawford,1997;王丽亚等,2012); 由于前期受到明显的井孔存储效应和皮肤效应(又称薄壁效应)的影响(Rasmussen,Crawford,1997;Toll,Rasmussen,2007;王丽亚等,2012),随着滞后时间的增加,大灰厂井、 大甸子井和三号地井的阶跃响应函数均呈增加趋势,后期阶跃响应函数(又称最佳阶跃响应函数)变化相对平稳,转变成相应的含水层类型. 因此从井-含水层系统的承压性强弱来看,大甸子井最强,三号地井次之,大灰厂井最弱.
表 2 6口井的水位对气压的阶跃响应函数与滞后时间的关系统计Table 2. Statistics on relationship between step response function of well water level to barometric pressure and lag time for the six wells井点
名称拟合方程 R2 标准差 地下水
类型*气压系数
/(mm·hPa-1)M2波潮汐因子
/(mm/10-9)板桥 A(i)=0.1994exp(-0.09361i)+0.0345 0.827 0.0193 非承压水和半承压水 4.00 2.150 大灰厂 A(i)=-0.06935exp(-1.487i)+0.1223 0.525 0.0201 承压水 1.80 0.157 黄骅 A(i)=0.2644exp(-0.01281i)-0.2078 0.775 0.0068 非承压水和半承压水 1.95 1.258 大甸子 A(i)=-0.1718exp(-0.86i)+0.2919 0.987 0.0063 承压水 3.20 0.979 丰镇 A(i)=0.09519exp(-0.2452i)+0.1029 0.988 0.0035 非承压水和半承压水 2.00 0.235 三号地 A(i)=-0.05837exp(-0.4529i)+0.2609 0.890 0.0069 承压水 2.10 0.337 注: R为阶跃响应函数与滞后时间的拟合值和计算值间的相关系数. 3.3 井潮效应和气压效应对结果的印证
对于承压井-含水层系统来说,一般情况下,其承压性越强,则水位对固体潮和气压的响应也越大. 但井水位的气压效率(系数)受到多种因素制约,主要困素为含水层的岩性和力学性质(张昭栋等,1986,1989,1991). 而影响井-含水层系统对固体潮响应的因素主要有含水层的水文地质特征、 井孔结构和固体潮汐波频率(Rojstaczer,1988;李春洪等,1990)等.
利用前述提及的获取井水位气压系数和M2潮汐因子的方法,对板桥井、 大灰厂井、 黄骅井、 大甸子井、 丰镇井和三号地井等各井在研究时段内的气压系数和M2波潮汐因子进行计算,分析比较井潮效应与气压效应,并利用井水位对气压的阶跃响应函数进行地下水类型判别的一致性和差异性分析,结果显示: 大灰厂井、 大甸子井和三号地井的井水位对气压的阶跃响应函数与气压系数和M2波潮汐因子具有明显的一致性,即对于这3口承压井而言,其井水位对气压的最佳阶跃响应函数值越大,相应的气压系数和M2波潮汐因子也越大,反之亦然(表 2).此外,具有潜水和半承压水性质的板桥井、 黄骅井和丰镇井,其水位对气压的最佳阶跃响应函数与气压系数和M2波潮汐因子之间的关系并不明显.
3. 讨论与结论
本文研究的板桥井、 大灰厂井、 黄骅井、 大甸子井、 丰镇井和三号地井等6口井中,各井的水位对气压的滞后时间与阶跃响应函数之间存在明显的以e为底的指数函数关系,且底数e的系数的正负,决定了井-含水层系统的地下水类型.
对于具有承压性质的井(譬如大灰厂井、 大甸子井和三号地井),其阶跃响应函数随着滞后时间的增大而增大,且最佳阶跃响应函数值越大,相应的气压系数和M2 波潮汐因子也越大; 对于具有潜水和半承压性质的井(例如板桥井、 黄骅井和丰镇井),其阶跃响应函数随着滞后时间的增大而减小,但最佳阶跃响应函数与气压系数和M2波潮汐因子间的关系不明显,可能与含水层的水力特性、 井孔结构和固体潮汐波频率有关.
按照地下水的贮存埋藏条件(水文地质方法)确定的地下水类型与本文通过阶跃响应函数方法确定的地下水类型大都不一致(大甸子井除外). 究其原因,很可能与各井含水层的水文地质特征、 井孔结构等有关.
通过水位对气压的阶跃响应函数的方法判别地下水类型,是基于水位与大气压力和潮汐应力的密切关系,而不需要考虑构造、 岩性、 地貌和成因等方面的因素,方法简单,在堪选测点及甄别观测资料质量和信度等方面具有一定的借鉴意义; 尤其对判别为具有承压性的井孔,可结合其最佳阶跃响应函数与气压系数和M2波潮汐因子之间的明显一致性,对地下水类型进行综合判定和检验.
本文仅以6口井为例,利用井水位对气压的阶跃响应函数进行地下水类型的判别研究,其结果是否具有普适性,尚需大量细致和深入的研究.
-
表 1 本研究使用的6口井的基本参数
Table 1 General information of six wells used in this study
井点名称 井深/m 含水层岩性 地下水类型* 水位埋深/m 资料选取时段 板桥 283.60 硅质石灰岩 裂隙承压水 39.60 2011-01—2011-12 大灰厂 102.00 砂页岩 孔隙裂隙混合水 14.50 2011-01—2011-12 黄骅 1250.00 灰岩 裂隙承压水 5.20 2007-01—2007-12 大甸子 200.76 砂岩、 砂板岩 裂隙承压水 18.80 2002-01—2002-12 丰镇 98.99 砂砾岩 承压水 2.36 2014-06—2015-05 三号地 100.00 玄武岩 孔隙裂隙潜水 51.20 2013-01—2013-12 * 地下水类型依据储存埋藏条件定性判别而得. 表 2 6口井的水位对气压的阶跃响应函数与滞后时间的关系统计
Table 2 Statistics on relationship between step response function of well water level to barometric pressure and lag time for the six wells
井点
名称拟合方程 R2 标准差 地下水
类型*气压系数
/(mm·hPa-1)M2波潮汐因子
/(mm/10-9)板桥 A(i)=0.1994exp(-0.09361i)+0.0345 0.827 0.0193 非承压水和半承压水 4.00 2.150 大灰厂 A(i)=-0.06935exp(-1.487i)+0.1223 0.525 0.0201 承压水 1.80 0.157 黄骅 A(i)=0.2644exp(-0.01281i)-0.2078 0.775 0.0068 非承压水和半承压水 1.95 1.258 大甸子 A(i)=-0.1718exp(-0.86i)+0.2919 0.987 0.0063 承压水 3.20 0.979 丰镇 A(i)=0.09519exp(-0.2452i)+0.1029 0.988 0.0035 非承压水和半承压水 2.00 0.235 三号地 A(i)=-0.05837exp(-0.4529i)+0.2609 0.890 0.0069 承压水 2.10 0.337 注: R为阶跃响应函数与滞后时间的拟合值和计算值间的相关系数. -
方慧娜. 2013. 利用地下水位气压效应反演汶川地震前后含水层参数的研究[D]. 北京: 中国地质大学(北京)地球科学与资源学院: 8-38. Fang H N. 2013. Estimating Aquifer Parameters From Barometric-Pressure Effect of Groundwater Before and After Wenchuan Earthquake[D]. Beijing: School of Earth Sciences and Resources, China University of Geosciences (Beijing): 8-38 (in Chinese).
国家地震局科技监测司. 1995. 地震地下水手册[M]. 北京: 地震出版社: 18-55. Department of Science and Technology Monitoring, State Seismological Bureau. 1995. Earthquake Ground Water Handbook[M]. Beijing: Seismological Press: 18-55 (in Chinese).
李春洪, 陈益惠, 田竹君. 1990. 井-含水层系统对固体潮的动态响应及其影响因素[J]. 中国地震, 6(2): 37-45. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD199002004.htm Li C H, Chen Y H, Tian Z J. 1990. The dynamic response of well-aquifer system to earth tides and its influence factors[J]. Earthquake Research in China, 6(2): 37-45 (in Chinese).
李悦, 姚会琴, 张杰卿, 邵永新. 2015. 2012年天津地区三次地震前水位对固体潮振幅响应计算分析[J]. 地震, 35(1): 131-139. http://www.cnki.com.cn/Article/CJFDTOTAL-DIZN201501014.htm Li Y, Yao H Q, Zhang J Q, Shao Y X. 2015. Responses of groundwater level to earth tides amplitude before three 2012 earthquakes in Tianjin area[J]. Earthquake, 35(1): 131-139 (in Chinese). http://www.baidu.com/link?url=75Tt0xXWZW5j9jN94ifRCsA_AtH_B7rsWoF6B1rVmsrMVfTj_vC7W2MqWpCL4eaMx9SEYxaKwcZBBKcSUsp5cyEcSTU2jpXR2atPozJ6_c8-VPsA7oITs4FPdDW1B7MDcyGtX_qwnvhWKSrqKe8pEGGP7GE2I4ajr9-GO9RjqS4c-o82BwQ4aZ-VQ1Xne5NNcNFgoq3Zgdb33QpqwLOQOb2ed-BM4rCyRVjvPBKkBtDVzFVmUlwoi7-8stdMGDyk6b1R8hud9joNZ3J50R2bnMdzyCviYGpNG2RXDl_XhUTMX8rLJugxOmtGWefKxQZKWcY2vVpx38mbycMBfx4t-Ol1CsaxcrgaHxb_L6RfQXwM3vPiIIJIXHgXM_dHZbWX&wd=&eqid=bfe8aace00020b8600000005588082f2
秦同洛, 李璗, 陈元千. 1989. 实用油藏工程方法[M]. 北京: 石油工业出版社: 64-66. Qin T L, Li D, Chen Y Q. 1989. Practical Methods of Reservoir Engineering[M]. Beijing: Petroleum Industry Press: 64-66 (in Chinese).
史浙明, 王广才. 2013. 承压含水层地下水位固体潮潮汐因子和相位滞后与汶川地震的关系[J]. 中国科学: 地球科学, 43(7): 1132-1140. http://www.cnki.com.cn/Article/CJFDTOTAL-JDXK201307007.htm Shi Z M, Wang G C. 2013. Relationship between the Earth tidal factor and phase lag of groundwater levels in confined aquifers and the Wenchuan MS8.0 earthquake of 2008[J]. Science China Earth Sciences, 56(10): 1722-1730. doi: 10.1007/s11430-013-4605-6
王大纯, 张人权, 史毅虹. 1995. 水文地质学基础[M]. 北京: 地质出版社: 23-29. Wang D C, Zhang R Q, Shi Y H. 1995. General Hydrogeology[M]. Beijing: Geological Publishing House: 23-29 (in Chinese).
王丽亚, 郭海朋, 李文鹏, 范珊珊, 朱菊艳, 凤蔚. 2012. 气压对观测井水位的影响及校正方法[J]. 水文地质工程地质, 39(6): 29-34. http://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201206009.htm Wang L Y, Guo H P, Li W P, Fan S S, Zhu J Y, Feng W. 2012. Impact of atmospheric loading on the water level in a well and methods for calibrating it[J]. Hydrogeology and Engineering Geology, 39(6): 29-34 (in Chinese). http://www.baidu.com/link?url=Kx6DugBi_feyncBnZz8fgcB6MRKT9WXVxKWVyGYFHM8lMF9vSe6lrhFZRWet8MHyrY6BBwtZbB-Oeb6ACihkvf7KVvun--DuoLAJ1Ll5C92q1Dzj2WbewebQS6JRNkwYWeRWMgTekQDYsNA2Fys7IH2TSEOGvfM1qqBDI1C6Is6AmhX7hyiyixsdk4nCtMmUAe2f3Tgw6QQN2q8NfybHcjvvhlucTMqXmp3TyjMAnImyCLQHrul8_CZw7eBohFlKpn1KFycGSse8qlXDon_Qb7vum3ZBn-ICCjiAMEBaIcxujOeYDOMcNXYIZAHizjLTFtWEwly7qq9yo_j2gWdENadJvSCzB3o5Y_-crZcY1ri&wd=&eqid=c1831156000234840000000558808312
杨柳, 马建英, 曹井泉, 邵永新, 刘文兵. 2014. 利用华北地区承压井水位资料反演含水层体应变[J]. 中国地震, 30(2): 249-259. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD201402013.htm Yang L, Ma J Y, Cao J Q, Shao Y X, Liu W B. 2014. Inversion of the volumetric strain of aquifer according to the tidal effect of groundwater in the North China region[J]. Earthquake Research in China, 30(2): 249-259 (in Chinese).
张昭栋, 郑金涵, 冯初刚. 1986. 气压对水井水位观测的影响[J]. 地震, (1): 42-46. http://www.cnki.com.cn/Article/CJFDTOTAL-DIZN198601006.htm Zhang Z D, Zheng J H, Feng C G. 1986. Effects of atmospheric pressure on observations of well water level variations[J]. Earthquake, (1): 42-46 (in Chinese). http://www.baidu.com/link?url=GdIYbRol-eOgyoYA1n6uFZtDwuwBAsIGrtI2-gwjyMouIKi4vBqCpu2KAQnOsguxbkdoa0sPapylMCqSIo4DynFM0mm5g4ZyW9dEMDoa4i5G6QUhf_32u6CE6Tk6wi-IxrWs2cM6i3IcTrpddN3ateBsZNXP2dEv0DNVYzgXDNzAp4Py67gbcFgh32sSKKQ7gT9qCbkv3ENrf2ioVacZE59WZcHILxSn5T_axoheNc71KsrsVrIMGU2rCut4ptARV6Y7xyAuOjv5Zk2VNV1K-Cfs1Kkk2-yJZmjKUCkLmpii-anLAANDWmC_lQ5Co160fswal8gWDi26NxaacYCxKC6AYpQZpKgY_naa31TJMZ3&wd=&eqid=c21f1708000241a70000000558808352
张昭栋, 郑金涵, 冯初刚. 1989. 井水位的固体潮效应和气压效应与含水层参数间的定量关系[J]. 西北地震学报, 11(3): 47-52. http://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ198903006.htm Zhang Z D, Zheng J H, Feng C G. 1989. Quantitative relationship between the earth tide effect of well water level, the barometric pressure effect and the parameters of aquifers[J]. Northwestern Seismological Journal, 11(3): 47-52 (in Chinese). http://www.baidu.com/link?url=bFFrqwN3jXn7ZTlZDtBngM5EZlk2EYdC2aateTBfIhhlfMi4ePO609W7y8mDqOx5G_Bw12VejZIXG5KPs5JJHRsi8V8iooP9z4yfS2o4k_txz0vYXMt78THZQXjN7QRzSGljiMhCUDsDHA5M4lgSNmxGXo3-BUWGtkKLrVBmAdQlLS6oCqmX1OUC7Je1CaTGpk5OJCge99O6AgTAtsh_IwOoPgBWyKbtdSXMNWl4lKuNNTXedzFtFKRQTepZ7zQQBdWscXRmO3AaXFIS6mYxgFg-FbgazfbGpToCKwNU0rJ3vOTYr-LdOPphEDK0FL8BfY-7Q_vN6W10iJd1ryQstCWe8vXNONw3xVS2lFwuPZxvZ7bX-G7yJlErdZLZMffG0PQKIyiKSU8HGdrE6tka-GFzWcvgrpQ_DDTU0qd6uulXRNXm9LX_j0mZgQ9EBVG4&wd=&eqid=c45583420002303a000000055880836a
张昭栋, 郑金涵, 冯初刚. 1991. 深井水位的固体潮效应[J]. 地震学报, 13(1): 66-75. http://www.dzxb.org/Magazine/Show?id=28370 Zhang Z D, Zheng J H, Feng C G. 1991. Effect of earth tide on deep well water level[J]. Acta Seismologica Sinica, 13(1): 66-75 (in Chinese). http://www.dzxb.org/Magazine/Show?id=28370
赵丹, 王广才. 2013. 地下水位气压效应的消除及主要气压影响分波的识别[J]. 中国科学: 技术科学, 43(1): 79-86. http://www.cnki.com.cn/Article/CJFDTOTAL-JEXK201301010.htm Zhao D, Wang G C. 2013. Removing barometric pressure effects from groundwater level and identifying main influential constituents[J]. Science China Technological Sciences, 56(1): 129-136. doi: 10.1007/s11431-012-5021-4
Darner R A, Sheets R A. 2012. Using existing data to estimate aquifer properties, Great Lakes Region, USA[J]. Groundwater, 50(3): 477-484. doi: 10.1111/gwat.2012.50.issue-3
Hussein M E A, Odling N E, Clark R A. 2013. Borehole water level response to barometric pressure as an indicator of aquifer vulnerability[J]. Water Resour Res, 49(10): 7102-7119. doi: 10.1002/2013WR014134
Rasmussen T C, Crawford L A. 1997. Identifying and removing barometric pressure effects in confined and unconfined aquifers[J]. Groundwater, 35(3): 502-511. doi: 10.1111/gwat.1997.35.issue-3
Rojstaczer S. 1988. Determination of fluid flow properties from the response of water levels in wells to atmospheric loading[J]. Water Resour Res, 24(11): 1927-1938. doi: 10.1029/WR024i011p01927
Toll N J, Rasmussen T C. 2007. Removal of barometric pressure effects and earth tides from observed water levels[J]. Ground Water, 45(1): 101-105. doi: 10.1111/gwat.2007.45.issue-1
-
期刊类型引用(9)
1. 曹白伦,洪敏,段勇,匡福江,陈建坤. 2022年汤加火山喷发引起的云南地表气压变化及深井水位响应研究. 大地测量与地球动力学. 2025(01): 97-103 .  百度学术
百度学术
2. 李自芮,要利锐,丁风和,朱鹏涛,余思汗,贺嘉伟. 固原东山坡井地下水类型及水化学特征分析. 地震地磁观测与研究. 2023(01): 92-100 .  百度学术
百度学术
3. 丁风和,车用太,刘耀炜,贺嘉伟. 地震观测井地下水埋藏类型判定方法及依据. 地震研究. 2022(02): 284-289 .  百度学术
百度学术
4. 姚林鹏,吕芳,宫静芝. 山西省地下流体观测井地下水类型综合判定. 地震地磁观测与研究. 2022(02): 115-120 .  百度学术
百度学术
5. 丁风和,贺嘉伟,栾博文,杨学峰,储翔. 宁夏南部及邻区地震观测井地下水埋藏类型综合评价. 地震研究. 2022(04): 599-607 .  百度学术
百度学术
6. 朱鹏涛,丁风和,沈宁,贺嘉伟,李新艳,王晨曦. 海原甘盐池地震观测井水位动态特征分析. 地震工程学报. 2022(06): 1489-1496 .  百度学术
百度学术
7. 陈竞. 如何利用物探测井方法判定含水层. 科技视界. 2021(12): 77-78 .  百度学术
百度学术
8. 姜佳佳,冯建刚,曹玲玲,张昱,张丽琼. 临夏水位高值异常分析及预报效能检验. 高原地震. 2021(01): 7-15 .  百度学术
百度学术
9. 王晓涛,丁风和,贺嘉伟,马云举,马治宁. 宁夏海原红羊井水位、水温同步变化特征分析. 防灾减灾学报. 2020(03): 61-67 .  百度学术
百度学术
其他类型引用(2)




 下载:
下载: