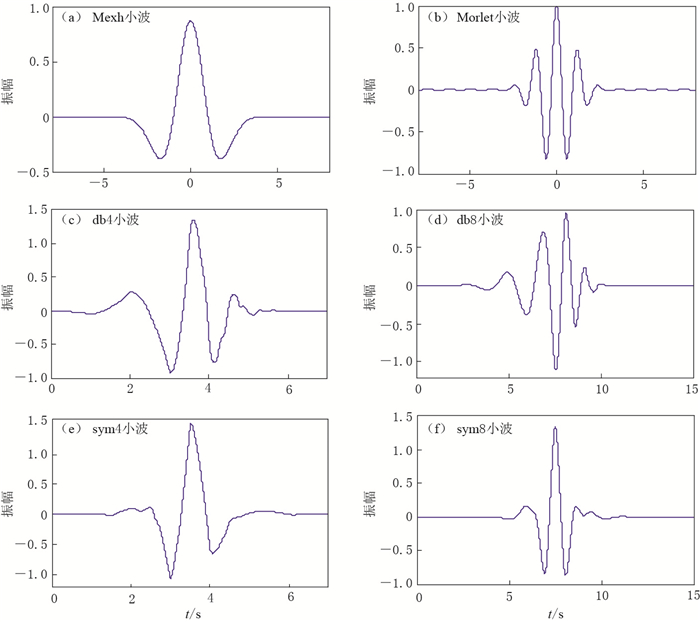
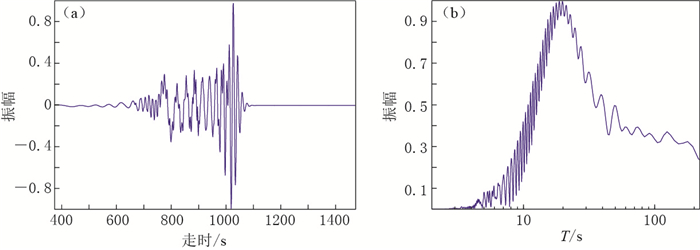
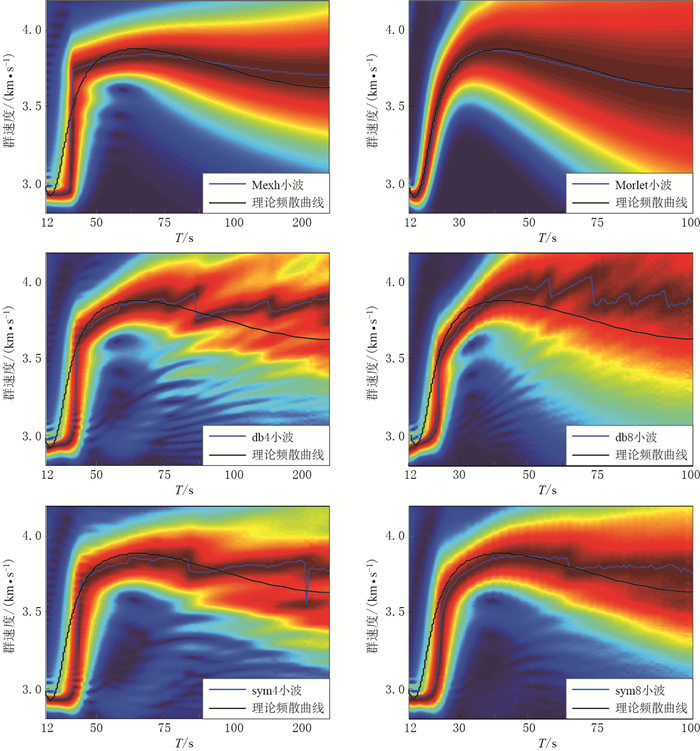
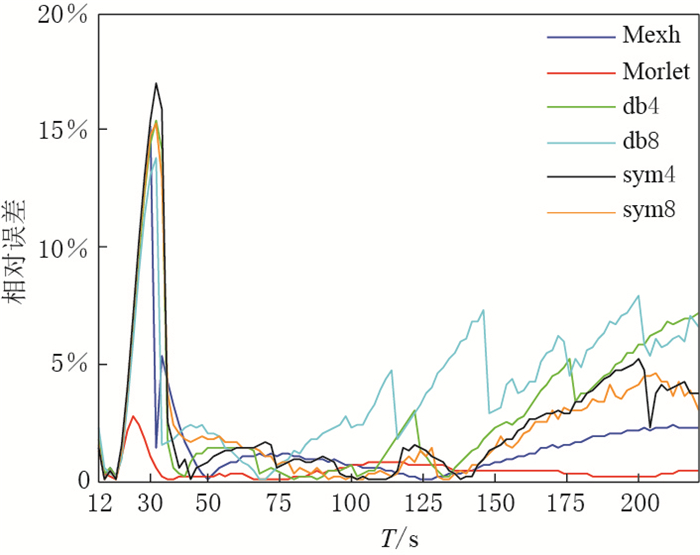
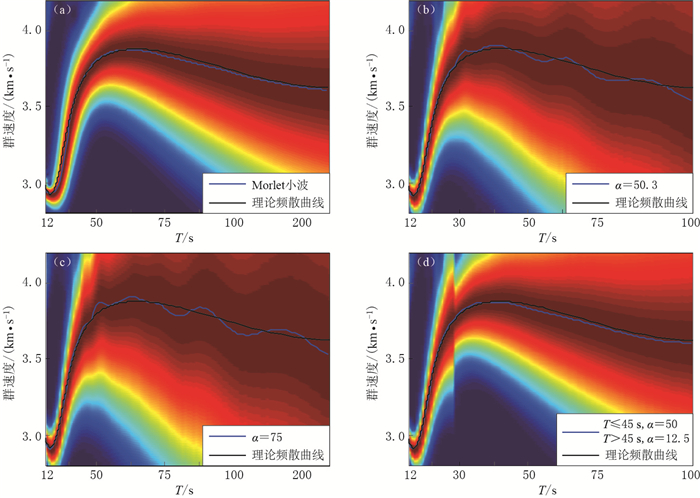
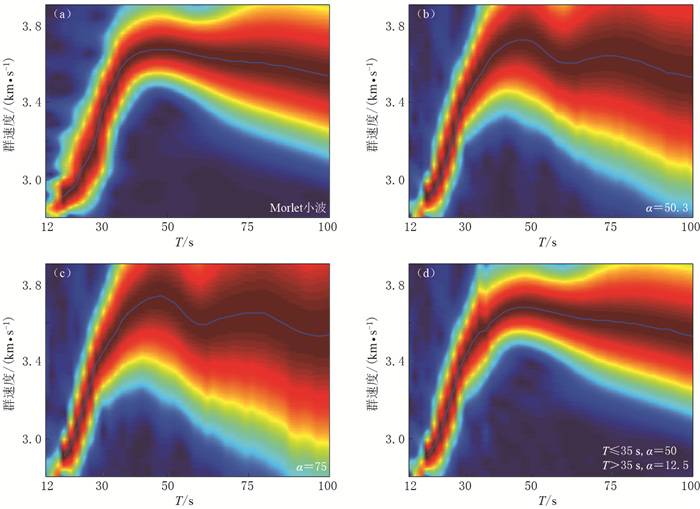
Measurement of surface wave group velocity using wavelet transform
-
摘要: 选取了几种常见的小波母函数，分别提取了同一理论下的面波数据的群速度，并与理论群速度进行对比，结果表明Morlet小波提取面波群速度的效果最好.此外，将Morlet小波与常用的多重滤波提取群速度的结果进行了比较，结果表明: ① 多重滤波法非常依赖高斯滤波系数α的取值，α的取值应随面波周期的增大而减小；② 在α取值得当的前提下，在20—35 s周期范围内多重滤波法提取面波群速度的相对误差比Morlet小波小，在周期大于35 s时，两者相对误差相近; ③ 合适的α值的选取需在不同周期段耗费大量时间进行大量试验，这说明多重滤波法不具备自适应性；而采用小波变换分析短周期信号时，时间窗变窄，频率窗变长，当分析长周期信号时，时间窗变长，频率窗变窄，具有对信号的自适应性，这是小波变换相比多重滤波法的最大优点.Abstract: Wavelet transform is proposed to measure surface wave group velocity in this paper. Several common mother wavelets are respectively used to calculate Rayleigh wave group velocities of the same synthetic seismograms, the results are compared with the theoretical group velocities. The comparison results indicate that Morlet wavelet is the most effective one in calculating group velocities. Furthermore, we compare Morlet wavelet transform with the most common used multiple filter technique in calculating group velocity, from which the following conclusions are drawn: ① multiple filter analysis method extremely depends on the value of Gaussain filter parameter α, and smaller value of α should be chosen during long period of surface wave; ② when the value of α is chosen adaptively, multiple filter analysis method is more accurate than Morlet wavelet transform in calculating group velocities when the period of surface wave is between 20 seconds and 35 seconds, while multiple filter analysis method has the similar accuracy with Morlet wavelet transform when the period of surface wave is over 35 seconds; ③ multiple filter analysis method will cost much more time to choose adaptive value of Gaussain filter parameter α for different periods without self-adaptivity to signals; however, wavelet transform can narrow the time window and lengthen the frequency window when analyzing short period signals and lengthen the time window and narrow the frequency window when analyzing long period signals with self-adaptivity to signals, which shows the outstanding advantage of wavelet transform over the multiple filter analysis method.
-
Keywords:
- surface wave /
- group velocity /
- wavelet transform /
- Morlet wavelet /
- multiple filter technique
-
引言
大量震害资料表明（Wood，1908；Seed，Idriss，1969；Seed et al，1988；李平等，2012），场地类别是影响地表地震动参数确定的重要因素之一。目前，我国由覆盖土层厚度和等效剪切波速划分场地的依据源于 《建筑抗震设计规范》 GB 50011—2010 （中国建筑科学研究院，2016），但是这两个指标的差异性对地表地震动的影响极其显著（文雯等，2012；陈卓识等，2015）。李红立和王贵珍（2012）关于不同场地条件对地震动参数影响的研究表明，随着覆盖土层厚度的增加，峰值加速度（peak ground acceleration，缩写为PGA）放大系数呈现先增大后减小的趋势。此外，随着场地类别从 Ⅰ 类到Ⅳ类，其对应的特征周期增大。梁久亮等（2015）通过构造若干典型土层剖面，利用一维等效线性化方法中基于频域的理论，研究覆盖土层厚度对地震动参数的影响，发现地表峰值加速度随覆盖土层厚度的增大呈现先增大后减小的趋势，而反应谱特征周期总体上随着覆盖层厚度的增加而逐渐增大；李平等（2010）、王国新和黄坤朋（2013）以及曹均锋等（2013）运用一维等效线性化方法研究土层剪切波速的变化对地震动参数的影响，其结果显示，当剪切波速减小时，设计反应谱平台值和地震动峰值加速度均减小，但反应谱特征周期变大。上述研究大多是基于现行 《建筑抗震设计规范》 规定的场地类别开展，而对于我国广泛分布的各类场地缺乏更加精细的研究。鉴于此，本文建立了包含四类场地的180个计算剖面，将其按照我国现有规范分类后进一步细分，以不同幅值的El Centro地震动作为输入地震动，采用一维等效线性化方法进行土层反应分析，计算得到场地地震动反应谱，将其规准化得到反应谱特征周期，探究细分之后场地类型对地表地震动反应谱特征周期的影响，以期为建筑物的抗震设防设计地震动参数的确定和相关规范的修订提供参考。
1. 土层地震反应分析方法
土层地震反应分析方法是研究场地地震动效应的重要方法之一，根据其本构模型及研究场地维数，可大致分为一维、二维和三维。虽然二维、三维模型更接近实际场地效应，但因其本构模型复杂、计算难度较大、不易掌握等因素未能得到广泛应用，目前地震工程界仍基本使用一维土层地震反应分析方法（周楷，2022）。一维土层地震反应分析方法常用的有传统等效线性化方法、频域相关等效线性化方法和时域非线性方法。考虑到本文是针对我国的场地类别进行详细的场地地震反应分析，选取我国工程界广泛应用的一维等效线性化方法，以便与国内主流方法保持一致而使其结果更为直观。等效线性化方法是间接考虑土体的非线性方法，其基本思想是使用等效剪切模量和阻尼比代替不同应变幅值下的剪切模量和阻尼比，将复杂的土体非线性计算转化成便于计算和建模的等效线性化计算（齐文浩，薄景山，2007；齐文浩等，2010；曹均锋等，2013）。1989年，廖振鹏院士提出了地表土层地震反应分析的等效线性化解法，并编制了相应的一维等效线性化计算程序LSSRLI-1，该方法至今仍是我国地震安全性评价中推荐的计算方法（廖振鹏，1989）。
2. 计算剖面和地震动输入
2.1 计算剖面
我国 GB 50011—2010 《建筑抗震设计规范》 （2016版）依据岩土名称和性状，将土层划分为岩石、坚硬土或软质岩石、中硬土、中软土、软弱土等五种类型，并给出各类型土对应的土层剪切波速范围，详情列于表1。
表 1 土的类型划分和剪切波速范围（引自中国建筑科学研究院，2016）Table 1. Classification of soil types and range of corresponding shear wave velocities （after China Academy of Building Research，2016）土的类型 岩土名称和性状 土层剪切波速
vS/（m·s−1）岩石 坚硬、较硬且完整的岩石 vS＞800 坚硬土或软质岩石 破碎、较破碎的岩石或软、较软的岩石，密实的碎石土 500＜vS≤800 中硬土 中密、稍密的碎石土，密实、中密的砾、粗、中砂，fak＞150 kPa的黏性土和粉土，坚硬黄土 250＜vS≤500 中软土 稍密的砾、粗、中砂，除松散外的细、粉砂，fak≤150 kPa的黏性土和粉土，fak＞130 kPa的填土，可塑性黄土 150＜vS≤250 软弱土 淤泥和淤泥质土，松散的砂，新近沉积的黏性土和粉土，fak≤130 kPa的填土，流塑性黄土 vS≤150 注：fak为荷载试验等方法得到的地基承载力特征值，vS为岩土剪切波速。 本文依据 《建筑抗震设计规范》 的场地类别划分建立了180个计算剖面进行场地分类。四个不同场地类别剖面的具体情况和土动力学参数详见李平（2010）。
本文I类场地的特点主要是覆盖土层厚度较薄且等效剪切波速范围分布较广，因此将Ⅰ类场地划分为四类，记为A1，A2，A3，A4类，其中：A1为软弱土，A2为中软土；硬类土按照等效剪切波速划分为A3和A4两类。Ⅱ类场地在我国分布广泛，且本文中Ⅱ类场地占比较高。为了细化研究，将Ⅱ类场地划分为四类，记为B1，B2，B3，B4类，其中：B1为软弱土，B2为中软土，B3和B4为中硬土。Ⅲ类场地的主要特点是场地覆盖土层厚度较大且土质较为软弱，因此将Ⅲ类场地分为软弱土C1类和中软土C2类。Ⅳ类场地主要为深厚的软弱土层，记为D类，共计10个剖面，分类结果列于表2。
表 2 四类场地模型分类情况Table 2. Classification of four classes of site models场地类别 土类号 H/m vSe/ （m·s−1） 剖面数量 I A1 0—3 vSe≤150 3 A2 0—3 150＜vSe≤250 7 A3 0—5 250＜vSe≤350 12 A4 0—5 350＜vSe ≤490 11 Ⅱ B1 3—15 60＜vSe≤150 10 B2 3—50 150＜vSe≤250 21 B3 5—90 250＜vSe≤350 34 B4 5—50 350＜vSe≤490 12 Ⅲ C1 15—80 60＜vSe≤150 25 C2 50—110 150＜vSe≤250 35 Ⅳ D 80—120 60＜vSe≤150 10 注：H为覆盖土层厚度，vSe为等效剪切波速。 2.2 输入地震动
El Centro地震动是人类记录到的第一条近场强地震动，被广泛应用于场地反应分析等研究。El Centro地震动频带范围宽，能较好地反映结构在地震作用下宽频率范围的响应特性。因此本文选择El Centro地震动作为输入地震动，并将其幅值分别调至50，100，200，300 cm/s2，以此来研究地震动峰值加速度对场地地震动参数的影响。峰值加速度为50 cm/s2的El Centro地震动加速度时程曲线和加速度反应谱如图1所示。
![]()
图 1 峰值加速度（PGA）为50 cm/s2的El Centro地震动加速度时程曲线 （a）及反应谱曲线 （b）Figure 1. Acceleration time history of El Centro seismic ground motion with PGA 50 cm/s2 （a） and corresponding response spectrum （b）3. 结果分析
基于180个场地计算剖面，将四条经调幅后的El Centro地震动作为输入地震动，在LSSRLI-1程序下进行土层地震反应分析计算，得到地表地震动参数，并对不同类别场地条件下的反应谱特征周期变化规律进行统计分析。
3.1 不同场地类别对反应谱特征周期的影响
采用差分进化法对计算所得地震反应谱进行规准（赵培培等，2017），得到特征周期Tg并对其进行分析。在研究反应谱特征周期时，本文将通过Tg随覆盖土层厚度变化的散点图进行趋势线拟合，进一步分析覆盖土层厚度对Tg的影响。各类场地特征周期随覆盖土层厚度的变化如图2—5所示。
![]()
图 2 输入不同PGA时Ⅰ类场地特征周期Tg 随覆盖土层厚度的变化Figure 2. Variation of characteristic period Tg of class Ⅰ site with depth of overburdens for different PGA inputs![]()
图 5 当60＜vSe≤150 m/s时不同PGA输入下Ⅳ类场地特征周期Tg随覆盖土层厚度的变化Figure 5. Variation of characteristic period Tg of class Ⅳ site with depth of overburden on the condition of 60＜vSe≤150 m/s for different PGA inputs对于Ⅰ类场地的A1，A2，A3，A4四个次类，相应剖面的反应谱特征周期均为0.65 s左右。由图2可知，在Ⅰ类场地中：当输入地震动强度为50—200 cm/s2时，Tg几乎不随着覆盖土层厚度的变化而变化；当输入地震动强度为300 cm/s2时，Tg随着覆盖土层厚度的增大而增大，反应谱向长周期方向移动。此外，可以看到反应谱特征周期在土层厚度大于2 m处突然下降，这是因为有些剖面存在的表层软弱土会导致反应谱特征周期减小（薄景山等，2003）。
由图3可见，在Ⅱ类场地中：当等效剪切波速60＜vSe≤250 m/s且覆盖土层厚度在3—50 m之间时，在输入四种不同强度地震动的情况下，特征周期Tg均随覆盖土层厚度的增加逐渐增大，且在同一覆盖土层厚度处输入基底的地震动强度越大，特征周期越大（图3a，b）；当250＜vSe≤490 m/s且覆盖土层厚度在5—90 m之间时，在输入四种不同强度地震动的情况下，Tg随着覆盖土层厚度的增大呈现先减小后增大的趋势，输入的地震动强度越大，增大趋势越明显（图3c，d）。
![]()
图 3 输入不同PGA时Ⅱ类场地特征周期Tg随覆盖土层厚度的变化Figure 3. Variation of characteristic period Tg of class Ⅱ site with depth of overburdens for different PGA inputs（a） 60＜vSe≤150 m/s；（b） 150＜vSe≤250 m/s；（c） 250＜vSe≤350 m/s；（d） 350＜vSe≤490 m/s由图4a可知，在Ⅲ类场地中，当等效剪切波速60＜vSe≤150 m/s且覆盖土层厚度在15—80 m之间时，输入相同强度的地震动，反应谱特征周期随覆盖土层厚度的增大整体呈增大趋势，且在同一土层厚度处输入的地震动强度越大，其特征周期越大。由图4b可知，在Ⅲ类场地中，当等效剪切波速150＜vSe≤250 m/s且覆盖土层厚度在50—110 m之间时，输入相同强度的地震动，反应谱特征周期随覆盖土层厚度的增加逐渐增大，且当输入相同强度的地震动时，对应的反应谱特征周期增长得更明显。
![]()
图 4 输入不同PGA时Ⅲ类场地特征周期Tg随覆盖土层厚度的变化Figure 4. Variation of characteristic period Tg of class Ⅲ site with depth of overburdens for different PGA inputs（a） 60＜vSe≤150 m/s；（b） 150＜vSe≤250 m/s由图5可知，在Ⅳ类软弱场地中，当60＜vSe≤150 m/s时反应谱特征周期随覆盖土层厚度的增大整体呈增大趋势。
3.2 不同场地类别反应谱特征周期参考值的确定
对计算所得结果进行统计分析，给出本文细分后场地类别反应谱特征周期的建议值。首先剔除数据中可能存在的异常值，使数值均在正负一倍标准差之内，再计算各类场地典型剖面的反应谱特征周期平均值，最终给出不同场地类别的特征周期建议值，结果列于表3。
表 3 不同场地类别的特征周期建议值Table 3. Reference values for the characteristic periods of different classes of sites场地类别 不同输入地震动峰值加速度下的特征周期/s 50 cm/s2 100 cm/s2 200 cm/s2 300 cm/s2 Ⅰ A1，A2，A3，A4 0.65 0.65 0.65 0.65 Ⅱ B4 0.70 0.70 0.70 0.70 B3 0.70 0.70 0.75 0.80 B2 0.70 0.75 0.90 1.00 B1 0.70 0.85 1.20 1.35 平均值 0.70 0.75 0.90 0.95 Ⅲ C2 0.75 0.80 0.95 1.15 C1 0.90 1.05 1.35 1.80 平均值 0.80 0.90 1.15 1.50 Ⅳ D 1.05 1.35 2.10 2.30 由表3分析可知：Ⅰ类场地，在不同地震动强度作用下的A1，A2，A3和A4类场地，反应谱特征周期不随场地类别的变化而变化，其反应谱特征周期参考值可取0.65 s；在Ⅱ类场地中，当输入地震动强度为50 cm/s2时，细分后的场地类别对反应谱特征周期的影响不大，其反应谱特征周期参考值可取0.7 s，然而当输入地震动强度为100—300 cm/s2时，B1类场地反应谱特征周期明显大于B4类场地，且随着输入地震动幅值的增大二者差值越大，这说明反应谱特征周期受等效剪切波速的影响比受覆盖土层厚度的影响更大；在Ⅲ类场地中，C1类场地反应谱特征周期明显大于C2类场地，同时随着输入地震动幅值的增大二者差值越大。在这四类场地中，输入相同强度的地震动，场地类别从Ⅰ类到Ⅳ类，反应谱特征周期逐渐增大。根据我国现行的场地类别划分准则，在同一类场地下，反应谱特征周期范围较大，因此在实际工程中，应对场地类别进行细分，更精确地选取反应谱特征周期。
3.3 结果验证
由于篇幅有限，本文选取西昌C2类场地的三个计算剖面和三河燕郊地区C2类场地的四个计算剖面，这些场地的剖面资料是通过收集整理实际钻孔资料获得（李平，2010）。选用四条不同幅值的El Centro地震动作为输入地震动，对每个剖面采用一维等效线性化方法进行计算，再使用差分进化法对土层地震反应分析得到的反应谱进行标定，从而得到特征周期，计算结果如表4所示。可见：总体结果满足本文所得到的规律，C2类场地的特征周期建议值对于输入地震动强度为中小强度地震的情况较适用；对于大震情况特征周期平均值基本适用，但是特征周期变化范围稍大，还需进一步深入研究。
表 4 典型剖面特征周期计算值与平均值Table 4. Calculated values and their average of characteristic periods for typical profiles输入地震动强度
/（cm·s−2）特征周期计算值/s 特征周期均值/s 50 0.65 0.70 0.70 0.70 0.85 0.85 0.85 0.75 100 0.75 0.75 0.75 0.75 0.85 0.85 0.90 0.80 200 1.05 0.80 0.75 0.80 0.90 1.05 1.05 0.95 300 1.20 0.85 0.85 0.90 1.05 1.20 1.20 1.05 4. 讨论与结论
本文建立了180个计算剖面，将不同幅值的El Centro地震动作为输入地震动，运用LSSRLI-1程序对各剖面进行土层地震反应分析计算，研究不同场地类别下加速度反应谱特征周期的变化，得出以下结论：① 在Ⅰ类场地中，随场地覆盖土层厚度的增加，反应谱特征周期基本不变；在Ⅱ类场地中，输入相同强度的地震动时，B1和B2类剖面的反应谱特征周期随覆盖土层厚度的增大而增大，B3和B4类剖面随覆盖土层厚度的增大，反应谱特征周期均呈现先减小后增大的趋势；在Ⅲ类和Ⅳ类场地中，输入相同强度的地震动时，反应谱特征周期随覆盖土层厚度的增大整体呈增大趋势。对于Ⅱ类和Ⅲ类场地而言，在同类场地中随着等效剪切波速的增大，其地表反应谱特征周期呈减小趋势；除Ⅰ类场地外，其余三类场地的特征周期均随基岩输入地震动强度的增大而增大。② 在不同类别场地中，当输入相同强度的地震动时，场地类别从 Ⅰ 类到Ⅳ类，反应谱特征周期逐渐增大。对四类场地来说，存在B1类场地特征周期大于C2类场地特征周期的异常情况，这主要是因为B1类场地属于等效剪切波速较小的浅层软弱土，C2类场地属于等效剪切波速较大的中厚层中软土，反应谱特征周期受等效剪切波速的影响较覆盖土层厚度的影响更大。③ 本文通过LSSRLI-1程序进行土层反应分析计算，因其计算方法自身的局限性以及土体非线性对地震动的影响，计算软弱土层和软夹层时会夸大土体的非线性影响，可能导致个别计算结果准确性不高，但不影响结果大体走向。④ 本文给出了细分后不同场地类别下反应谱特征周期建议值，并进行了验证，表明该结果可丰富场地地震动效应研究，亦可为场地地震动参数提供依据。
另一方面，本文仍存在许多不足之处值得讨论。① 本文选取具有代表性的C2类场地7个计算剖面进行特征周期建议值的验证，结果表明特征周期建议值对于输入地震动强度为50—100 cm/s2的情况更适用，对于输入更大地震动的情况尚需进一步的研究。② 本文Ⅰ类和Ⅳ类场地所选择的计算剖面较少，但场地类别对反应谱特征周期的影响规律能基本呈现。若想较全面地探究不同场地类别对反应谱特征周期的影响，尚需收集大量实际的场地剖面信息进行更为详细的计算分析。③ 基于强震记录结合场地条件分析是研究场地条件对地震动影响最有效和最可靠的手段，本文只采用了不同幅值的El Centro地震动作为输入地震动，未能采用多种强震记录进行分析，因此应结合强震记录和场地勘察数据开展进一步相关研究。
-
![]()
图 2 理论瑞雷面波垂向分量波形(a)和振幅谱(b)
Figure 2. Vertical component synthetic seismogram of Rayleigh wave (a) and its amplitude spectra (b)
![]()
图 3 不同小波母函数提取的面波群速度与理论群速度对比
Figure 3. Comparison between surface wave group velocities obtained from different wavelet generating functions with theoretical values
![]()
图 4 不同小波母函数提取面波群速度的相对误差
Figure 4. Relative errors of surface wave group velocities obtained from different wavelet generating functions
![]()
图 5 Morlet小波和多重滤波提取面波群速度与理论面波群速度对比
Figure 5. Comparison between surface wave group velocities obtained from Morlet wavelet transform and multiple filter technique with theoretical values
![]()
图 6 Morlet小波和多重滤波法提取面波群速度的相对误差
Figure 6. Relative errors of surface wave group velocities obtained by Morlet wavelet transform and multiple filter technique
![]()
图 7 南岭西部地区某台站记录到的MW7.1地震垂直分量瑞雷面波波形(a)和振幅谱(b)
Figure 7. Vertical component seismogram of Rayleigh wave (a) and its amplitude spectra (b) of MW7.1 earthquake recordod by one station in western Nanling region
-
曹小林, 张雪梅, 朱介寿. 1999.中国及邻区的地震面波频散反演[J].成都理工学院学报, 26(3): 295-298. https://www.researchgate.net/publication/298494957_Surface_wave_dispersion_inversion_in_China_and_adjacent_regions Cao X L, Zhang X M, Zhu J S. 1999. Surface wave dispersion inversion in China and adjacent regions[J]. Journal of Chengdu University of Technology, 26(3): 295-298 (in Chinese). https://www.researchgate.net/publication/298494957_Surface_wave_dispersion_inversion_in_China_and_adjacent_regions
陈浩朋, 朱良保, 王清东, 杨颖航, 张攀. 2014.面波群速度测量误差分析[J].地球物理学进展, 29(5): 1985-1995. doi: 10.6038/pg20140501 Chen H P, Zhu L B, Wang Q D, Yang Y H, Zhang P. 2014. An error analysis of surface wave group velocity measurement[J]. Progress in Geophysics, 29(5): 1985-1995 (in Chinese). doi: 10.6038/pg20140501
陈立, 薛梅, Plon L K, 杨挺. 2012.南海瑞雷面波群速度层析成像及其地球动力学意义[J].地震学报, 34(6): 754-772. https://www.researchgate.net/publication/272503488_Group_velocity_tomography_of_Rayleigh_waves_in_South_China_Sea_and_its_geodynamic_implications Chen L, Xue M, Plon L K, Yang T. 2012. Group velocity tomography of Rayleigh waves in South China Sea and its geodynamic implications[J]. Acta Seismologica Sinica, 34(6): 754-772 (in Chinese). https://www.researchgate.net/publication/272503488_Group_velocity_tomography_of_Rayleigh_waves_in_South_China_Sea_and_its_geodynamic_implications
房立华, 吴建平, 王未来, 王长在, 杨婷. 2013.华北地区勒夫波噪声层析成像研究[J].地球物理学报, 56(7): 2268-2277. doi: 10.6038/cjg20130714 Fang L H, Wu J P, Wang W L, Wang C Z, Yang T. 2013. Love wave tomography from ambient seismic noise in North-China[J]. Chinese Journal of Geophysics, 56(7): 2268-2277 (in Chinese). doi: 10.6038/cjg20130714
何正勤, 丁志峰, 叶太兰, 孙为国, 张乃铃. 2001.中国大陆及其邻域地壳上地幔速度结构的面波层析成像研究[J].地震学报, 23(6): 596-603. http://mall.cnki.net/magazine/Article/DZXY200106004.htm He Z Q, Ding Z F, Ye T L, Sun W G, Zhang N L. 2001. Surface wave tomography of the crust and upper mantle of Chinese mainland[J]. Acta Seismologica Sinica, 23(6): 596-603 (in Chinese). http://mall.cnki.net/magazine/Article/DZXY200106004.htm
潘佳铁, 吴庆举, 李永华, 张风雪, 张广成. 2011.华北地区瑞雷面波相速度层析成像[J].地球物理学报, 54(1): 67-76. http://manu39.magtech.com.cn/Geophy/EN/abstract/abstract7718.shtml Pan J T, Wu Q J, Li Y H, Zhang F X, Zhang G C. 2011. Rayleigh wave tomography of the phase velocity in North China[J]. Chinese Journal of Geophysics, 54(1): 67-76 (in Chinese). http://manu39.magtech.com.cn/Geophy/EN/abstract/abstract7718.shtml
王敏玲, 陈赟, 梁晓峰, 徐逸鹤, 范宇婷, 徐涛, 张忠杰, 滕吉文. 2015.华南及南海北部地区瑞利面波层析成像[J].地球物理学报, 58(6): 1963-1975. doi: 10.6038/cjg20150612 Wang M L, Chen Y, Liang X F, Xu Y H, Fan Y T, Xu T, Zhang Z J, Teng J W. 2015. Surface wave tomography for South China and the northern South China Sea area[J]. Chinese Journal of Geophysics, 58(6): 1963-1975 (in Chinese). doi: 10.6038/cjg20150612
余大新, 吴庆举, 王鹏, 叶庆东, 潘佳铁, 高孟潭. 2016.蒙古中南部地区基于天然地震的勒夫波相速度层析成像[J].地震学报, 38(1): 41-52. doi: 10.11939/jass.2016.01.004 Yu D X, Wu Q J, Wang P, Ye Q D, Pan J T, Gao M T. 2016. Love wave phase velocity tomography in the south-central Mongolia from earthquakes[J]. Acta Seismologica Sinica, 38(1): 41-52 (in Chinese). doi: 10.11939/jass.2016.01.004
周青云, 何永峰, 靳平, 廖桂生. 2006.利用多重滤波方法提取面波频散曲线[J].西北地震学报, 28(1): 46-50. http://en.cnki.com.cn/Article_en/CJFDTOTAL-ZBDZ200601009.htm Zhou Q Y, He Y F, Jin P, Liao G S. 2006. Using MFT obtain Rayleigh-wave dispersion curve[J]. Northwestern Seismological Journal, 28(1): 46-50 (in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-ZBDZ200601009.htm
朱介寿, 曹家敏, 蔡学林, 严忠琼, 曹小林. 2002.东亚及西太平洋边缘海高分辨率面波层析成像[J].地球物理学报, 45(5): 646-664. http://manu39.magtech.com.cn/Geophy/EN/Y2002/V45/I05/646 Zhu J S, Cao J M, Cai X L, Yan Z Q, Cao X L. 2002. High resolution surface wave tomography in East Asia and West Pacific marginal seas[J]. Chinese Journal of Geophysics, 45(5): 646-664 (in Chinese). http://manu39.magtech.com.cn/Geophy/EN/Y2002/V45/I05/646
朱良保, 熊安丽. 2007.面波频散测量的频时分析法[J].地震地磁观测与研究, 28(1): 1-13. http://en.cnki.com.cn/Article_en/CJFDTOTAL-DZGJ200701000.htm Zhu L B, Xiong A L. 2007. The frequency-time analysis method for surface wave dispersion measurement[J]. Seismological and Geomagnetic Observation and Research, 28(1): 1-13 (in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DZGJ200701000.htm
Cara M. 1973. Filtering of dispersed wavetrains[J]. Geophys J Int, 33(1): 65-80. doi: 10.1111/j.1365-246X.1973.tb03415.x
Daubechies I. 1988. Orthonormal bases of compactly supported wavelets[J]. Commun Pure Appl Math, 41(7): 909-996. doi: 10.1002/(ISSN)1097-0312
Daubechies I. 1990. The wavelet transform, time-frequency localization and signal analysis[J]. IEEE Trans Inf Theory, 36(5): 961-1005. doi: 10.1109/18.57199
Dziewonski A, Bloch S, Landisman M. 1969. A technique for the analysis of transient seismic signals[J]. Bull Seismol Soc Am, 59(1): 427-444. http://citeseerx.ist.psu.edu/showciting?cid=973577
Herrmann R B, Ammon C J. 2004. Computer programs in seismology, 3.30[CP/OL]. [2013-08-20]. http://www.eas.slu.edu/eqc/eqccps.html.
Inston H H, Marshall P D, Blamey C. 1971. Optimization of filter bandwidth in spectral analysis of wavetrains[J]. Geophys J Int, 23(2): 243-250. doi: 10.1111/gji.1971.23.issue-2
Kennett B L N, Engdahl E R, Buland R. 1995. Constraints on seismic velocities in the Earth from traveltimes[J]. Geophys J Int, 122(1): 108-124. doi: 10.1111/gji.1995.122.issue-1
Kolínský P. 2004. Surface wave dispersion curves of Eurasian earthquakes: The SVAL program[J]. Acta Geodyn Geomater, 1(2): 165-185. https://www.researchgate.net/publication/295315410_Surface_waves_dispersion_curves_of_eurasian_earthquakes_The_SVAL_program
Landisman M, Dziewonski A, Satȏ Y. 1969. Recent improvements in the analysis of surface wave observations[J]. Geophys J Int, 17(4): 369-403. doi: 10.1111/gji.1969.17.issue-4
Levshin A, Pisarenko V F, Pogrebinsky G A. 1972. On a frequency-time analysis of oscillations[J]. Ann Geophys, 28(2): 211-218. https://www.researchgate.net/publication/284699529_On_a_frequency-time_analysis_of_oscillations
Morlet J, Arens G, Fourgeau E, Giard D. 1982. Wave propagation and sampling theory, Part Ⅱ: Sampling theory and complex waves[J]. Geophysics, 47(2): 222-236. doi: 10.1190/1.1441329
Nyman D C, Landisman M. 1977. The display-equalized filter for frequency-time analysis[J]. Bull Seismol Soc Am, 67(2): 393-404. http://www.bssaonline.org/content/67/2/393.short
Wu Q J, Zheng X F, Pan J T, Zhang F X, Zhang G C. 2009. Measurement of interstation phase velocity by wavelet transformation[J]. Earthquake Science, 22(4): 425-429. doi: 10.1007/s11589-009-0425-3
-
期刊类型引用(1)
1. 刘芳，杨聪昆，周宏宇. 既有钻芯RC框架结构抗震性能研究. 西安工业大学学报. 2024(06): 733-742 . 
百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 933
- HTML全文浏览量: 561
- PDF下载量: 44
- 被引次数: 1
