Influence law of ground motion parameters on soil slope seismic response
-
摘要: 选取了具有不同峰值加速度、频谱和持时的6组地震动加速度时程作为输入,基于有限元数值模拟方法建立了二维均质边坡有限元模型,模拟分析了不同地震动作用下边坡模型的加速度和位移响应,揭示了地震动峰值加速度、频谱和持时对土坡地震响应的影响作用及其规律.研究结果显示:地震动峰值加速度、频谱和持时对土坡地震响应均有显著的影响,其中,边坡坡脚处和坡肩处的变形位移随地震动峰值加速度、特征周期和持时的增大而增大,坡体临空面各点的峰值加速度放大系数呈现随输入地震动特征周期的增大而增大、随输入地震动峰值加速度的增大而减小的规律.研究结果可为地震作用下边坡稳定性设计及防治研究提供参考.Abstract: Six groups of strong ground motion records with different characteristic parameters were selected as seismic input, a two-dimensional slope model with homogeneous soil was established based on the finite element numerical simulation method, and then the acceleration and displacement responses of the slope model were calculated and analyzed. Finally the influence degree and laws of the PGA, frequency spectrum and duration on the slope responses in earthquakes were revealed. The results showed that the PGA, characteristic period and duration all had an significant effect on slope seismic response. It was also indicated that the displacement of the slope foot and shoulder evidently increased with increase of the PGA, characteristic period and duration of earthquakes, and the amplification coefficients of PGA along the slope free surface also increased with increase of characteristic period while decreased with increase of the PGA. The result can provide reference for the design and prevention of slope stability under earthquake effect.
-
Keywords:
- ground motion parameters /
- soil slope /
- dynamic response /
- influence laws
-
引言
地震往往会触发大量山体滑坡等地质灾害. 2008年5月12日发生在我国四川省汶川县的MS8.0大地震引发了3万5000多处滑坡(黄润秋,2009),给当地人们的生命和财产造成了严重的损害.地震作用下的边坡动力稳定性问题一直备受国内外相关专家的关注.近些年来对众多地震滑坡震害现象的实际调查和理论试验研究(祁生文等,2003;徐光兴等,2008;黄润秋,2009; 殷跃平,2009)表明,地震动的幅值、频谱和持时这3个要素对地震边坡稳定性均有着不同程度的影响作用,地震动中不同幅值、频谱和持时的组合决定了地震作用下边坡等结构物的受灾程度(胡聿贤,1981).
峰值加速度是被较早接受的表征地震动强弱的参数,是控制地震动荷载对边坡稳定性影响的主要参数之一,也是边坡地震稳定性研究中使用最多的一个参数.目前已有较多研究通过现场调查或数值模拟方法进行了关于地震动峰值加速度对边坡动力响应的影响特性研究,并取得了很多成果(Wilson,Keefer,1985;Harp,Wilson,1995;Griffiths, Lane, 1999;祁生文等,2003;徐光兴等,2008;王秀英等,2009;言兴志等,2011).由于地震动频谱和持时较峰值加速度获取要相对复杂一些,因此针对地震动频谱和持时对边坡稳定性影响特性的研究较少,尤其在震后快速评估边坡稳定性时,选用峰值加速度这一指标具有一定的优势,但事实和已有研究均表明,具有不同频谱和持时的地震动对边坡稳定性的影响作用存在显著差异,因此,亟需对这些参数对边坡动力响应的影响规律加以研究.鉴于此, 本文拟基于有限元模拟方法选取不同幅值、频谱和持时的地震动加速度时程作为荷载输入,计算分析地震动参数对土质边坡响应的影响规律,以期为边坡地震稳定性的评价和地震动参数指标选取提供参考.
1. 计算模型与分析方法
1.1 边坡模型
为研究边坡在地震作用下的动力响应特性,建立如图 1所示的边坡模型.该模型参考徐光兴等(2008),并在其基础上,将模型尺寸扩大,以便进一步消除边界影响.有限元模型如图 1所示,长为170 m,高为70 m,边坡坡角为34°,坡高30 m,边坡坡顶后缘长度为80 m.模型材料为均质材料;边坡土体的密度为2 070 kg/m3,弹性模量为90.8 MPa,泊松比为0.3,黏聚力为13.99 kPa,内摩擦角为25°.
![]() 图 1 边坡有限元模型示意图(修改自徐光兴等,2008)Figure 1. Schematic diagram of soil slope finite element model (modified from Xu et al, 2008)
图 1 边坡有限元模型示意图(修改自徐光兴等,2008)Figure 1. Schematic diagram of soil slope finite element model (modified from Xu et al, 2008)1.2 动力方程与求解方法
对于边坡地震动力稳定性问题可以建立以下基本力学运动方程:

(1) 式中:M为质量矩阵,C为阻尼矩阵,K为刚度矩阵;



地震是一种完全随时间变化的复杂荷载,边坡岩土体在地震作用下往往会进入弹塑性状态,这时便无法得到解析解,解析方法也不再适用,但通过数值计算可以得到结构动力反应的数值解.常用的数值计算方法有分段解析法、中心差分法、平均常加速度法、线性加速度法、纽马克(Newmark)-β法和威尔逊(Wilson)-θ法,这些方法的核心是假定结构在每一个微小时间步长内呈线弹性反应,通过逐步积分来获取该结构在整个时域内的最终响应.在有限元模拟软件ABAQUS中有隐式和显式两种算法,其中隐式算法是以纽马克-β法为基础,而显式算法是采用中心差分法来解决动力学问题.本文采用隐式算法.
1.3 土体本构模型
对于边坡土体材料,本文的模拟分析选用理想弹塑性本构模型,屈服准则采用摩尔-库仑破坏准则.该破坏准则广泛应用于岩土材料的理论与实践中.
1.4 边界条件
在模拟分析边坡等半无限体的动力问题时,为了防止地震波传播至模型边界处反射回模型,通常需要设置人工边界,允许必要的能量发散.目前用于解决动力问题边界条件设置的方法主要有简单截断边界、黏弹性边界、透射边界等,这些方法各有利弊, 其中黏弹性边界较为简单且适用性强,可较好地用于边坡地震稳定性问题中,因此本文采用黏弹性边界(刘晶波等,2006),其中二维黏弹性人工边界等效物理系统的弹簧系数K和阻尼系数C可分别由下式求得:

(2) 
(3) 式中:KBN和KBT分别为弹簧法向、切向刚度;ρ为介质质量密度;αT和αN分别为切向、法向黏弹性人工边界参数,二者的取值范围通常分别为0.35—0.65和0.8—1.2(刘晶波等,2006),本文取其中值,即αT=0.5,αN=1.0;R为波源至人工边界点的距离;cS和cP分别为S波和P波波速,G为介质剪切模量,可通过下式分别求得:

(4) 
(5) 
(6) 式中,E和υ分别为结构材料的弹性模量和泊松比.
1.5 阻尼参数的确定
阻尼的设置是模拟计算中的一个关键环节,工程中常常采用瑞雷阻尼,即通过质量矩阵和刚度矩阵的线性组合来表述:C=αM+βK,其中α为质量阻尼系数,β为刚度阻尼系数.当计算选用的两阶阻尼比与结构阻尼比相等时,α和β可由下式确定:

(7) 
(8) 式中,ω1和ω2为结构前两阶振型的圆频率.经计算,本文中边坡模型的前两阶圆频率分别为4.96 rad/s和5.45 rad/s,阻尼比ξ一般取0.05即可满足计算要求.
2. 输入地震动
地震荷载采用输入实际地震动记录加速度时程来实现,输入至模型底部的水平方向.选取6条特征周期Tg分别集中在0.25,0.35,0.45,0.55,0.65和0.90 s的地震动记录,过滤掉20 Hz以上的高频成分,并将加速度幅值统一调整为1 m/s2,截取时长为19.98 s. 图 2给出了所记录的6条地震动加速度时程及其相应的反应谱曲线.
为模拟分析加速度幅值大小对边坡动力响应的影响,本文选取特征周期Tg=0.45 s的地震动加速度时程作为输入,将峰值加速度分别调整至1, 2, 3和4 m/s2,持时均设定为19.98 s.
为研究持时对边坡稳定性的影响,对于一条峰值加速度绝对值为amax的地震动时程而言,将其持时定义为加速度的绝对值a0首次与末次超过amax/3的持续时间(胡聿贤,1981).据此可以得到输入Tg=0.45 s的地震动加速度时程的持时为Td=7.5 s,如图 3所示.
3. 计算结果分析
3.1 地震动输入以及人工边界施加效果验证
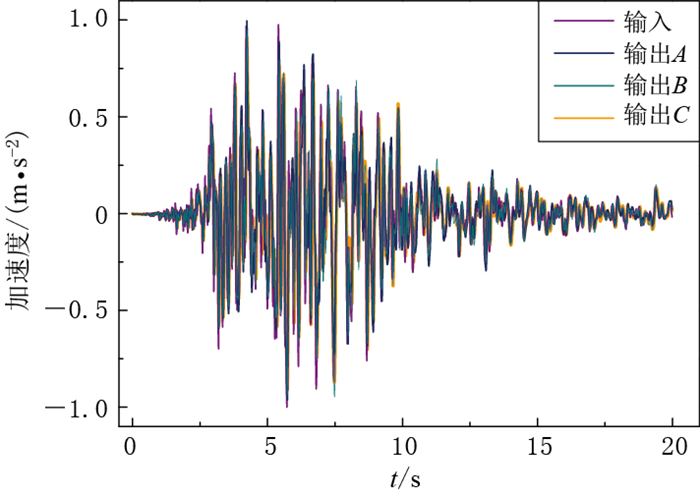
地震荷载以及合理地施加人工边界是确保计算模拟正确性的前提.为了更全面地验证地震荷载和所施加人工边界的效果,在程序完成计算后,提取图 1中模型底部观测点A, B, C的加速度时程并进行对比分析,结果如图 4所示.可知,输出与输入的加速度时程曲线吻合程度较高,较好地验证了地震动时程输入的正确性和所施加人工边界的良好效果.
3.2 地震动峰值加速度的影响
提取各地震动输入下各观测点的加速度、变形位移响应曲线和PGA放大系数,以分析峰值加速度对边坡响应的影响特性.
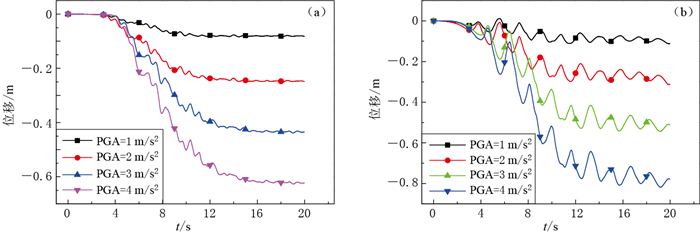
分别提取变形最为显著的坡肩处P1点的竖向变形位移时程和坡脚处P5点的水平向变形位移曲线,结果如图 5a和图 5b所示.可以看出,在P1和P5点,坡体反应的变形位移均随着输入地震动峰值加速度的增大而显著增大, 且输入的峰值加速度每增加1 m/s2,坡脚处P5点和坡肩处P1点的变形均增加0.2 m左右,这表明峰值加速度对边坡变形具有显著影响.
![]() 图 5 不同峰值加速度地震动输入下坡肩处P1点的竖向位移时程(a)和坡脚处P5点的水平位移时程(b). P1和P5点的位置见图 1Figure 5. Time-histories of vertical displacement of the point P1 at the slope shoulder (a) and horizontal displacement of the point P5 at the slope foot (b) under different input PGAs The locations of the points P1 and P5 are shown in Fig. 1
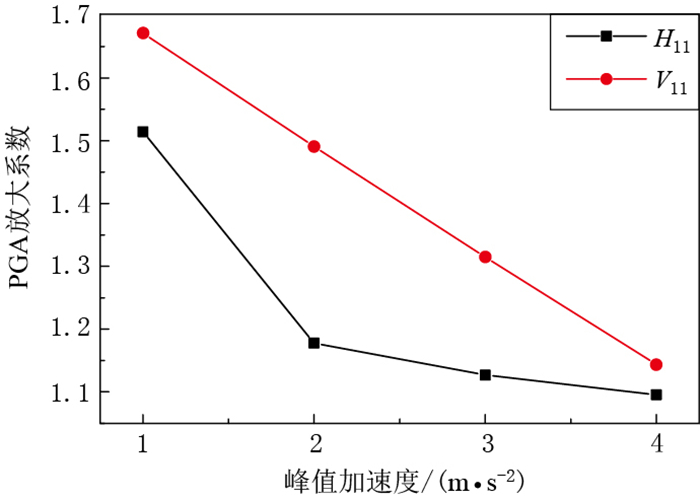
图 5 不同峰值加速度地震动输入下坡肩处P1点的竖向位移时程(a)和坡脚处P5点的水平位移时程(b). P1和P5点的位置见图 1Figure 5. Time-histories of vertical displacement of the point P1 at the slope shoulder (a) and horizontal displacement of the point P5 at the slope foot (b) under different input PGAs The locations of the points P1 and P5 are shown in Fig. 1为研究坡体对PGA的放大规律,选择坡顶V11点和坡面H11点(其位置见图 1)两处来分析,图 6给出了这两点在不同峰值加速度地震动输入下PGA放大作用的变化.可见,坡体对输入PGA的放大作用随着输入地震动PGA的增大呈减小的趋势.当输入峰值为1 m/s2时,坡顶V11点和坡面H11点两处对输入PGA分别放大了1.52倍和1.68倍;随着地震动PGA增大至4 m/s2,两观测点处的PGA放大系数分别减小至1.10倍和1.15倍.这可能是由于随着输入地震动PGA的增大,土体内部剪应变增大而导致阻尼增大,滤波作用增强,抑制了PGA的放大效果.
3.3 地震动频谱的影响
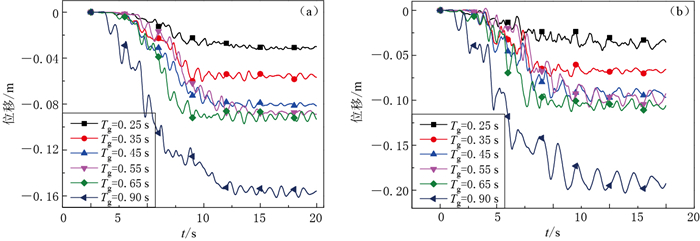
同样选取边坡变形最明显的坡肩处P1点的竖向变形位移时程和坡脚处P5点的水平向变形位移和响应作为分析对象,其变形位移曲线分别如图 7a和7b所示.
由图 7可知,随着输入地震动特征周期Tg的增大,边坡坡脚处和坡肩处的变形位移均逐渐增大.在特征周期Tg为0.45,0.55和0.65 s时的地震动作用下的边坡变形位移响应之间的变化相对于特征周期Tg为0.25和0.35 s时的小;但当输入地震动特征周期约为0.90 s时,观测点变形位移均明显增大.
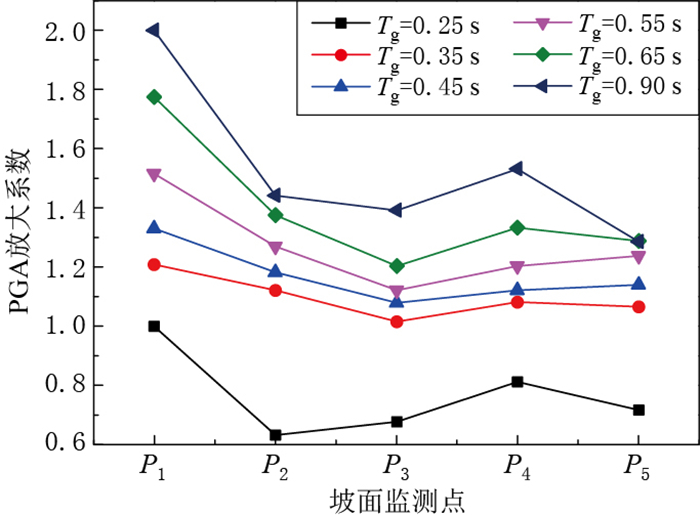
为研究地震动特征周期对边坡PGA放大作用的影响,提取坡面各观测点在不同特征周期地震动作用下响应的峰值加速度,如图 8所示.可以看出,随着输入地震动特征周期的增大,坡面各点的PGA放大系数总体呈增大的趋势.
以上研究结果表明,输入地震动的特征周期对边坡响应的影响也十分显著,但规律较峰值加速度的要复杂.
3.4 地震动持时的影响
由图 5可以看出:在地震刚刚开始时,地震动加速度幅值较小,坡体尚处于弹性阶段,坡体观测点变形位移在零点附近波动;随着输入地震动加速度幅值的增大,动力作用增强,坡体变形位移迅速增大;直到第12 s左右,坡体观测点的变形位移在随后的地震动持续时间里基本维持不变,此时边坡产生了永久变形.整个地震动过程中坡体的变形在地震动持时Td阶段内变化较为显著,不断地增大,这说明坡体变形位移受地震动持时的影响也十分显著.
4. 讨论与结论
分析边坡地震稳定性时需要考虑地震动特性对其的影响作用,地震动特性主要表现为加速度时程的幅值、频谱和持时等3个要素.本文采用单因素变量法,分别选取不同单一特性的地震动作为输入来分析其对边坡响应的影响作用,结果显示地震动的各个特性对边坡稳定性均有不同程度的影响.
PGA对边坡稳定性有显著的影响.边坡坡脚处和坡肩处的变形随地震动PGA的增大而单调增大,坡顶处PGA放大系数随着输入地震动PGA的增大呈现减小的规律,这可能是由于随着输入地震动PGA的增大,土体内部剪应变增大导致阻尼增大,坡体内部阻尼呈现明显的非线性状态,滤波作用明显增强,抑制了PGA的放大效应.
另一方面,地震动的频谱特性对边坡稳定性也有明显的影响.随着输入地震动特征周期的增大,边坡坡脚处和坡肩处的位移逐渐增大,特别是当特征周期大于0.65 s时,坡体位移响应明显增大,同时坡顶的PGA放大系数也基本上呈增大趋势.然而地震动频谱特性的影响规律较峰值加速度的复杂.此外,持时对边坡稳定性也有一定的影响.
综上,地震动特性参数中PGA幅值和频谱对边坡稳定性的影响效果较为明显,在边坡地震稳定性分析评价中应作为重点考虑因素.
-
图 1 边坡有限元模型示意图(修改自徐光兴等,2008)
Figure 1. Schematic diagram of soil slope finite element model (modified from Xu et al, 2008)
图 5 不同峰值加速度地震动输入下坡肩处P1点的竖向位移时程(a)和坡脚处P5点的水平位移时程(b). P1和P5点的位置见图 1
Figure 5. Time-histories of vertical displacement of the point P1 at the slope shoulder (a) and horizontal displacement of the point P5 at the slope foot (b) under different input PGAs The locations of the points P1 and P5 are shown in Fig. 1
-
胡聿贤. 1981.地震工程学[M].北京:地震出版社: 100-103. Hu Y X. 1981. Earthquake Engineering[M]. Beijing: Seismological Press: 100-103 (in Chinese).
黄润秋. 2009.汶川8.0级地震触发崩滑灾害机制及其地质力学模式[J].岩石力学与工程学报, 28(6): 1239-1249. http://d.wanfangdata.com.cn/Periodical/yslxygcxb200906021 Huang R Q. 2009. Mechanism and geomechanical modes of landslide hazards triggered by Wenchuan 8.0 earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 28(6): 1239-1249 (in Chinese). http://d.wanfangdata.com.cn/Periodical/yslxygcxb200906021
刘晶波, 谷音, 杜义欣. 2006.一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报, 28(9): 1070-1075. http://d.wanfangdata.com.cn/Periodical/ytgcxb200609004 Liu J B, Gu Y, Du Y X. 2006. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements[J]. Chinese Journal of Geotechnical Engineering, 28(9): 1070-1075 (in Chinese). http://d.wanfangdata.com.cn/Periodical/ytgcxb200609004
祁生文, 伍法权, 孙进忠. 2003.边坡动力响应规律研究[J].中国科学: E辑, 33(增刊1): 28-40. http://d.wanfangdata.com.cn/Periodical/zgkx-ce2003z1004 Qi S W, Wu F Q, Sun J Z. 2003. Study on the dynamic response characteristic of slope[J]. Science in China: Series E, 33(S): 28-40. http://d.wanfangdata.com.cn/Periodical/zgkx-ce2003z1004
王秀英, 聂高众, 王登伟. 2009.利用强震记录分析汶川地震诱发滑坡[J].岩石力学与工程学报, 28(11): 2369-2376. doi: 10.3321/j.issn:1000-6915.2009.11.028 Wang X Y, Nie G Z, Wang D W. 2009. Analysis of landslide induced by Wenchuan earthquake by strong motion records[J]. Chinese Journal of Rock Mechanics and Engineering, 28(11): 2369-2376 (in Chinese). doi: 10.3321/j.issn:1000-6915.2009.11.028
言志信, 张森, 张学东, 张刘平. 2011.顺层岩质边坡地震动力响应及地震动参数影响研究[J].岩石力学与工程学报, 30(增刊2): 3522-3528. http://www.cqvip.com/QK/96026X/2011S2/1003580319.html Yan Z X, Zhang S, Zhang X D, Zhang L P. 2011. Study of dynamic response of bedding rock slope under earthquake and influence of ground motion parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 30(S2): 3522-3528 (in Chinese). http://www.cqvip.com/QK/96026X/2011S2/1003580319.html
徐光兴, 姚令侃, 李朝红, 高召宁. 2008.边坡地震动力响应规律及地震动参数影响研究[J].岩土工程学报, 30(6): 918-923. http://d.wanfangdata.com.cn/Periodical/ytgcxb200806022 Xu G X, Yao L K, Li Z H, Gao Z N. 2008. Dynamic response of slopes under earthquakes and influence of ground motion parameters[J]. Chinese Journal of Geotechnical Engineering, 30(6): 918-923 (in Chinese). http://d.wanfangdata.com.cn/Periodical/ytgcxb200806022
殷跃平. 2009.汶川八级地震滑坡特征分析[J].工程地质学报, 17(1): 29-38. http://d.wanfangdata.com.cn/Periodical/gcdzxb200901004 Yin Y P. 2009. Features of landslides triggered by the Wenchuan earthquake[J]. Journal of Engineering Geology, 17(1): 29-38 (in Chinese). http://d.wanfangdata.com.cn/Periodical/gcdzxb200901004
Griffiths D V, Lane P A. 1999. Slope stability analysis by finite elements[J]. Géotechnique, 49(3): 387-403. doi: 10.1680/geot.1999.49.3.387
Harp E L, Wilson R C. 1995. Shaking intensity thresholds for rock falls and slides: Evidence from 1987 Whittier Narrows and Superstition Hills earthquake strong-motion records[J]. Bull Seismol Soc Am, 85(6): 1739-1757. https://www.researchgate.net/publication/279937877_Shaking_intensity_thresholds_for_rock_falls_and_slides_evidence_from_1987_Whittier_Narrows_and_Superstition_Hills_earthquake_strong-_motion_records
Wilson R C, Keefer D K. 1985. Predicting areal limits of earthquake-induced landsliding[G]//Evaluating Earthquake Hazards in the Los Angeles Region: An Earth-Science Perspective. Washington: U.S. Geological Survey: 317-345.





 下载:
下载: