Self-noise tests on seismic dataloggers
-
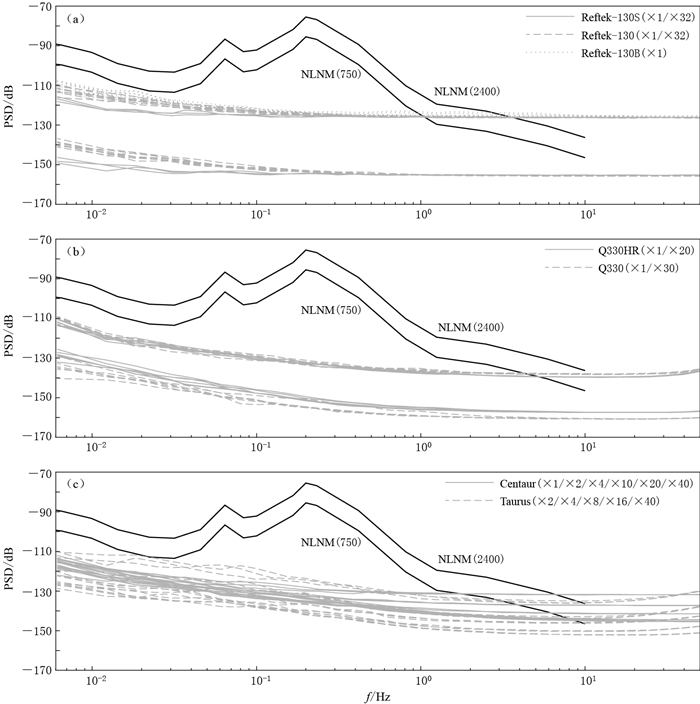
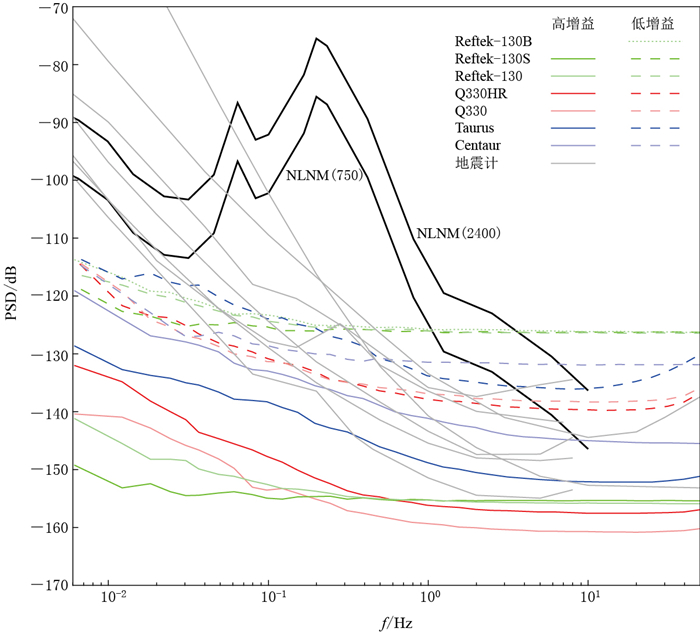
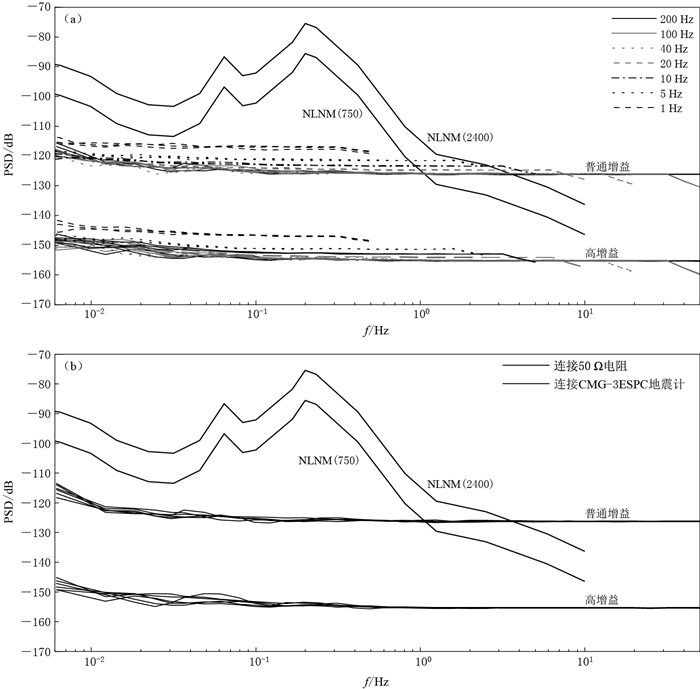
摘要: 本文采用多通道相关分析方法测量并分析研究了国内地震观测常用的6种进口地震数据采集器的自噪声.结果表明:6种进口地震数据采集器无论在普通增益还是高增益模式下,当频带范围处于1 Hz以下时,自噪声均低于NLNM低噪声模型(灵敏度按750 V·s/m换算);在低增益模式下,当频带范围处于1 Hz以上时,各数据采集器的自噪声与NLNM低噪声模型高低交错,须根据观测目的谨慎使用;Q330HRS和Reftek-130/130S型数据采集器的高增益模式较适合测量宽频带地震计的自噪声.Abstract: The self-noises of the seismic dataloggers have significant meaning for self-noise measurement of seismometers and dynamic range evaluation of broadband seimographs. In this study, we measured and analyzed the self-noises of six types of imported seismic dataloggers widely used in Chinese seismic observations based on multi-channel correlation analysis method. The results showed that self-noises of all six types of dataloggers are well below NLNM model when frequency domain is below 1 Hz in both high-gain and unity-gain modes by sensitivity conversion factor 750 V·s/m; however, for the frequency domain higher than 1 Hz, self-noises of the six types of dataloggers interlace with NLNM model, hence much care should be taken according to the goals of seismic observation. Reftek-130/130S and Q330HRS with high-gain sampling mode might be the preferable choice for the seismometer's self-noise measurements.
-
Keywords:
- seismic datalogger /
- self-noise /
- high-gain
-
-
表 1 检测所用地震数据采集器的具体参数
Table 1 The detailed parameters of seismic dataloggers used in the test
数据采集器型号 通道数 序列号 增益档及其对应量程 Reftek-130S 6 BD24, BD80 普通增益,±10 V;高增益,±0.3125 V Reftek-130 3 AF6C, AF74, AF85 普通增益,±10 V;高增益,±0.3125 V Reftek-130B 3 9B05, 9B5F, 9C86 普通增益,±10 V Q330HRS 6 4557, 4546 普通增益,±20 V;高增益(26位),±1 V(26位);普通增益,±20 V;高增益(24位),±0.67 V(24位) Taurus 3 002688 ×2,±1 V;×4,±2 V;×8,±4 V;×16,±8 V;×40,±20 V Centaur 3 000413 ×1,±0.5 V;×2,±1 V;×4,±2 V;×10,±5 V;×20,±10 V; ×40,±20 V -
滕云田, 胡星星, 王喜珍, 王晓美, 卢红娅, 王喆, 张旸. 2016.用多通道AD分级采集扩展地震数据采集器的动态范围[J].地球物理学报, 59(4): 1435-1445. doi: 10.6038/cjg20160424 Teng Y T, Hu X X, Wang X Z, Wang X M, Lu H Y, Wang Z, Zhang Y. 2016. Extending dynamic range of the seismic data acquisition system by using multi-channel ADC[J]. Chinese Journal of Geophysics, 59(4): 1435-1445 (in Chinese). doi: 10.6038/cjg20160424
Evans J R, Followill F, Hutt C R, Kromer R P, Nigbor R L, Ringler A T, Steim J M, Wielandt E. 2010. Method for calculating self-noise spectra and operating ranges for seismographic inertial sensors and recorders[J]. Seismol Res Lett, 81(4): 640-646. doi: 10.1785/gssrl.81.4.640
Holcomb G L. 1989. A Direct Method for Calculating Instrument Noise Levels in Side-By-Side Seismometer Evaluations[R]. Albuquerque, New Mexico: U.S. Geological Survey: 89-214.
Ringler A T, Hutt C R. 2010. Self-noise models of seismic instruments[J]. Seismol Res Lett, 81(6): 972-983. doi: 10.1785/gssrl.81.6.972
Sleeman R, van Wettum A, Trampert J. 2006. Three-channel correlation analysis: A new technique to measure instrumental noise of digitizers and seismic sensors[J]. Bull Seismol Soc Am, 96(1): 258-271. doi: 10.1785/0120050032
Sleeman R, Melichar P. 2012. A PDF representation of the STS-2 self-noise obtained from one year of data recorded in the Conrad Observatory, Austria[J]. Bull Seismol Soc Am, 102(2): 587-597. doi: 10.1785/0120110150
Welch P. 1967. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms[J]. IEEE Trans Audio Electroacous, 15(2): 70-73. doi: 10.1109/TAU.1967.1161901




 下载:
下载: