引言

国际地磁参考场模型(IGRF)是一个数字化的模型，用来计算1900年到现在的地球主磁场即地核磁场(Finlay et al，2010)． 它是由国际地磁与高空物理学协会(IAGA)的V-MOD工作组支持和赞助下的地磁模型团队建立和维护的． 1968年，IAGA正式给出了1965年的国际地磁参考场，而现在最新的是第11代国际地磁参考场模型(IGRF11)，以后每5年更新一次，主要是更新其中的高斯系数． 本文所使用的数据主要来自卫星的磁测、 天文台与地磁台站的地面观测、 海洋磁测和人工地磁勘测． 最新的主磁场模型及其长期变化模型被广泛应用于科学研究(如空间气象和磁异常现象)，团队和民间团体的地磁方向定位(地磁定位)，全球或区域地磁图的绘制，以及空白区域的地磁要素计算等．

1.   IGRF11模型的数学描述及其数据分析

IGRF11(Finlay et al，2010； Macmillan，Finlay，2011)由IAGA工作小组于2009年12月发布，该地磁参考场模型适用于1900—2015年． 它更新了2005—2010年的地球主磁场和2010—2015年的线性长期变化模型，并提供了第11代模型的球谐系数，发布了2010年的磁偏角、 磁倾角、 总磁场的地磁图和2010—2015年的变化率； 对南大西洋和磁极附近的一些不正常的变化给出了合理的解释(Heirtzler，2002； Macmillan et al，2009)．

1.1   数学描述

国际地磁参考场模型是采用球谐分析的方法来描述地球主磁场及其长期变化的一系列数学模型(Finlay et al，2010； Maus et al，2010； 徐文耀，2000； 安振昌，1992； 王亶文，2005)． 主磁场的高斯系数表达式为

在近地空间的无源区，起源于地球内部的主磁场可以表示为标量磁位V的负梯度，这里V可以展开为式(1)． 其中，r，θ，φ表示计算点的空间位置. r为距参考球球心的径向距离； a=6371.2 km是地磁参考半径，采用的是地球平均半径，为从格林威治起算的东经度； θ为地心余纬度(90度减去纬度). g_n^m和h_n^m为球谐系数，利用均匀分布于全球的足够多的测点值用最小二乘方法拟合求得； n和m分别是球谐函数的阶数和次数； P_n^m是n阶m次施密特准归一化缔合勒让德函数． 同时，IAGA的官方网站上推荐采用1984年世界大地测量坐标系(WGS84，a=6378.137 km，b=6356.752 km)，其精度明显优于1966年国际天文学联合会(IAU)坐标系(IAU66，a=6378.160 km，b=6356.775 km)． IGRF11不仅利用了传统的地面台站数据(包括分均值、 时均值、 年均值等)、 流动磁测数据(包括大陆磁测、 海洋磁测、 航空磁测等)，还利用了国际地球位场研究产生的近10年来的大量卫星磁测数据，包括德国的CHAMP卫星，丹麦的Ørsted卫星，阿根廷和美国的Ørsted-2/SAC-C卫星等． 为了充分利用这些高精度的数据，IAGA决定从2000年开始将主磁场的精度扩展到13阶，即n=13(2000年前的阶数为8或10，只能够精确到1 nT，而IGRF11模型可以精确到0.1 nT)． 因此，IGRF11模型共有195个泰勒系数n(n+2)，计算起来比较复杂．

This page contains the following errors:

Below is a rendering of the page up to the first error.

而长期变化系数的计算公式为

1.2   球谐系数

IGRF11模型(Finlay et al，2010； Macmillan，Finlay，2011)是基于2009年10月发布的候选模型建立的． 其中主磁场的确定基于7个候选模型，分别由Maus领队的美国国家海洋和大气管理局国家地球物理数据中心(NOAA/NGDC)，Thébault领队的法国巴黎地球物理学院(IPGP)，Olsen领队的丹麦科技大学国家太空研究所(DTU Space)，Lesur领队的德国国家地球科学研究中心(GFZ)，Bondar领队的俄罗斯磁层、 电离层和无线电传输研究所(IZMIRAN)、 Chambodut领队的法国地球物理研究所(EOST)和Hamilton领队的英国地质调查局(BGS)提供； 而长期变化模型则由以上7个团队和Kuang领队的美国国家航空航天局戈达德太空飞行中心(NASA/GSFC)提供．

This page contains the following errors:

Below is a rendering of the page up to the first error.

1.3   数据分析

由于篇幅所限，仅以NOAA/NGDC候选地磁场模型为例分析基于候选模型建立的IGRF11模型所采用的数据． NOAA/NGDC团队由来自NOAA/NGDC的Maus S和Manoj C以及来自GFZ的 Rauberg J，Michaelis I和Lühr H等人组成． 其提供的候选模型提供主磁场40阶和长期变化磁场16阶的球谐系数．

1.3.1   数据来源及其选取原则

NOAA/NGDC团队提供的候选模型是基于CHAMP和Ørsted卫星数据建立的，其中Ørsted卫星数据用来确定原始模型和估算不确定的高斯系数． 通过地面台站测量的地磁场数据分析出磁暴指数和地磁扰动强度，然后选取合适的数据． 同时，所有的卫星数据均采用卫星每隔20 s测量的地磁场数据进行二次抽样处理，相当于运行距离150 km． 分散的地磁场数据来自中纬度地区(60°S—60°N)和极区(>50°N和>50°S)，而矢量数据只用于中纬度地区． 中纬度地区的标量和矢量数据分别选自CHAMP卫星在当地时间22:00—5:00的测量数据和Ørsted卫星在当地时间20:00—5:00的测量数据，而所有极区的数据均采用当地时间卫星测量的矢量数据，没有换算成标量数据(Facius，Reitz，2007; Newitt et al，2009)． 本文采用的是POMME-6模型的建模原理，数据选取原则见表 1．

表  1  数据的选择标准

Table  1.  Data selection criteria

下载: 导出CSV 

| 显示表格

1.3.2   数据校正

1)通过磁力计系统和星象仪系统估算角度来修正矢量数据．

2)通过Kuvshinov和Olsen(2004)的预测模型减去在球谐角度45°时由于8种海洋潮汐现象引起的地磁感应场．

3)通过CHAMP卫星测量的实际电子密度和温度来纠正感应电流产生的抗磁效应．

2.   IGRF11模型误差分析

IGRF11(Finlay et al，2010； Macmillan，Finlay，2011)是一个简单易用，能满足大部分不同使用者需求，提供较高精度的地球表面和近地空间地磁数据的模型． 但它并不是一个十分完美的模型，其原因为： ① 模型的高斯系数以后不会再更新，这就使得模型的计算数值与真实值之间有很大差异； ② 由于截断阶数的限制，模型只表征了低频磁场(即长波长的磁场)，对于高频磁场则没有完全表征； ③ 由观测数据引起的误差很难消除．

系数的误差导致了模型的误差，因为在求解系数过程中，所用的数据大部分只经过简单的均方根处理． 由于地磁场随时间的变化而改变，在建模过程中，我们使用了卫星测量的覆盖全球的矢量数据(1979—1980年MAGSAT卫星数据和1999年以后的Ørsted和CHAMP卫星测量数据)． 这部分数据是相当精确的，但其它时间段数据则是通过地磁台站或者其它方式得到的，然后经过估计得到长期变化情况． 由于地磁台站测得的数据覆盖面积有限，所测数据并不能表征全球各个区域的地磁场随时间的变化情况，因此，建模本身就是一个误差来源，而估计模型的精度更是极其困难． 经过大量的数据统计，得到如下误差范围作为参考(Lowes，2000)：

1)主磁场误差来源． ① 1900—1940年模型给出的精度是50 nT，根据候选模型的数据和经验推断，精度在100 nT左右更为合适； ② 1945—1960年，误差在1945年的300 nT到1960年的100 nT之间； ③1965—1995年，误差在50 nT更为合理； ④ 2000年以后，由于卫星数据的应用，误差在2000年的10 nT到2005年的5 nT之间； ⑤ 最近时间的误差，由于卫星数据质量的降低，建议误差在10 nT左右．

2)长期变化磁场误差来源． 通过5年的时间估计长期变化磁场的年变化率是很不准确的，而且这种变化并不呈线性增长，在1年中各个月份的变化也有很大差异. 因此，采用线性的年变化率20 nT/a是及其错误的，这无疑增加了模型的误差．

3)数据处理等人为因素引起的误差．

4)地壳异常场引起的误差． IGRF11模型反映的是地球主磁场的模型，即地核磁场，并没有包括地壳异常场，例如地球表面的地质特征(山脉、 海洋、 矿物质等)引起的短波长的磁场大约为200—300 nT．

5)观测数据本身的误差． ① 人类活动的影响(交通、 直流高压输电线路等)，使得在测量时数据并没有反映地磁场的真实情况； ② 自然条件的影响(太阳磁暴、 静日变化等)，一天内数值变化在20 nT左右，而磁暴时可达到1000 nT．

3.   IGRF11模型与WMM2010模型对比

3.1   世界地磁场模型WMM2010

世界地磁场模型WMM2010(Maus et al，2010； 李忠亮，边少锋，2011)由美国国家地理空间情报局(NGA)和英国国防地球影像制图与情报局(DGlA)提供资金，美国国家海洋和大气管理局国家地球物理数据中心和英国地质调查局制作，并由NGA发布，是美国国防部、 英国国防部、 北约、 世界水文署导航与姿态／航向参考系统采用的标准模型，被广泛用于民用导航系统，其有效期为2010—2015年． WMM2010模型所用数据的来源主要为磁测卫星(Ørsted和CHAMP)和地面磁测站(全球152个)，包括世界数据中心所收集的全球数据． 在模型5年有限期内，采用均方根法对全球测量值与模型理论值的差进行分析，限定磁偏角D和磁倾角I优于1°，磁北向分量X和东向分量Y优于140 nT，水平分量H和垂直分量Z优于200 nT，总磁场强度F优于280 nT． WMM2010模型主要反映的是源自地球外核流体产生的长波部分，而地壳、 上地幔、 电离层、 磁气层和地表感生电流产生的磁场基本上都没有体现，其局限性与IGRF11类似．

3.2   数据对比分析

根据两个模型发布的高斯系数，利用球谐模型求得地磁要素值． 为直观地表达模型之间差异的根源，通过同一条件下(同一经度、 纬度、 时间和实测值)的地磁场数值对比和模型的高斯系数进行说明．

由于获取实测数据的时间为2007年5月，而模型计算时间为2011年9月，需要对实测数据进行修正． 选取WMM系列模型对实测值进行主磁场长期变化修正，能使修正后的数据更接近真实数据． 修正过程中，在经纬度相同条件下以2007年5月—2009年12月为第一阶段，采用WMM2005模型对实测值进行修正； 2010年1月—2011年9月为第二阶段，采用WMM2010模型对实测值进行修正，最终获得补偿值(表 2)． 表 2中经纬度相同条件下由上至下的3行数值分别为实测值、 修正值和补偿值，其中修正值的左列为第一阶段数据，右列为第二阶段数据．

表  2  实测数据修正

Table  2.  Correction of experimental data

下载: 导出CSV 

| 显示表格

将获得的补偿值与WMM2010和IGRF11两个模型的计算值进行了比较. 表 3中经纬度相同条件下由上至下的4个值分别为补偿值、 WMM2010计算值、 IGRF11计算值和IGRF11模型检验值．

表  3  单点位置磁场要素值

Table  3.  Magnetic elements of a single spot

下载: 导出CSV 

| 显示表格

为有效说明数据的可靠性，计算了表 3中的模型计算值相对于修正后的实测数据的误差大小，如表 4所示．

表  4  误差分析

Table  4.  Error analysis

下载: 导出CSV 

| 显示表格

根据表 4中实测值与模型计算值的对比，可得出如下结论： 在正常磁场环境下，模型计算值与实测值比较接近(地壳、 上地幔、 电离层、 磁气层和地表感生电流产生的磁场基本上没有体现在模型之中)； WMM2010的最大绝对误差和最大相对误差都优于IGRF11，总体上WMM2010比IGRF11模型的计算精度高3倍左右； 官方发布的一些结论也证实了WMM2010模型的计算精度较IGRF11模型要高． 考虑到外界地磁的干扰、 测量误差、 测量手段、 测量环境及时间等因素的影响，特别是在模型没有考虑地壳磁异常场情况下，IGRF11的总场强度最大绝对误差为121.6 nT，最大相对误差为0.64％，其它分量要素误差也能控制在较小范围，因此，这样的误差范围是合理的． 综上所述，实现的两种模型在精度上可以满足我们日常计算的需求，具有广阔的应用环境．

根据表 5中官方发布的两个模型的高斯球谐系数(Maus et al，2010； Finlay et al，2010)，可知模型的差异主要来自系数的差异，即不同模型在估算系数时的差异. 其中主磁场部分变化不大，这与地球的固有属性相关. 而差别主要集中在长期变化部分，因为这部分是不能测量和准确估计的． 因此，模型系数的准确性一方面来自所用数据的可靠性，另一方面在于长期系数的估算，而模型精度的提高也主要集中在这两方面．

表  5  球谐系数的比较

Table  5.  The spherical harmonic coefficients

下载: 导出CSV 

| 显示表格

4.   IGRF11模型与WMM2010模型可视化

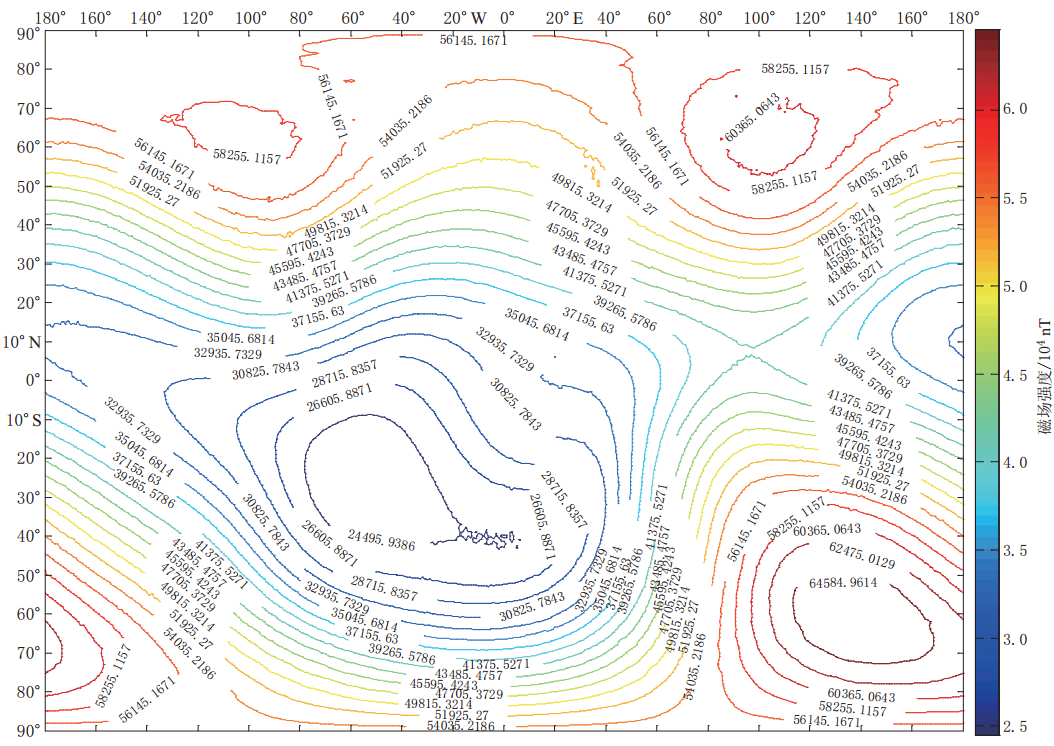
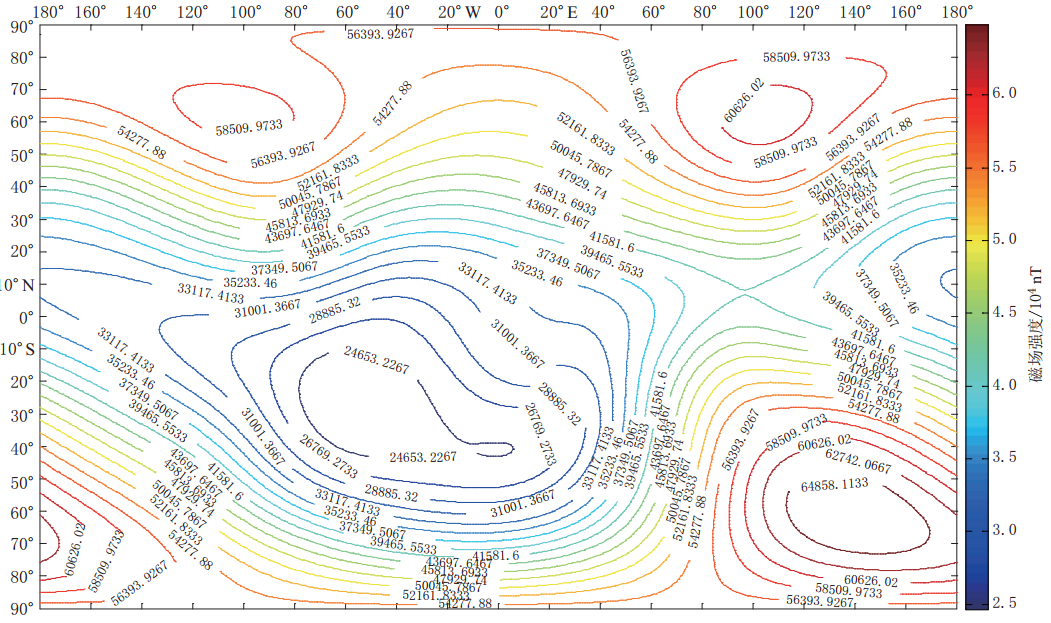
在MATLAB环境下，通过研制的可视化软件绘制了WMM2010(图 1)和IGRF11(图 2)总磁场强度的等值线图． 对两者进行比较，分析其异同点，并结合上一节的数值对比，来验证模型的精度和适用范围．

图  1  WMM2010总磁场强度等值线图

Figure  1.  Contour map of total field intensity of WMM2010

下载: 全尺寸图片 幻灯片

图  2  IGRF11总磁场强度等值线图

Figure  2.  Contour map of total field intensity of IGRF11

下载: 全尺寸图片 幻灯片

利用官方发布的高斯系数(Maus et al，2010； Finlay et al，2010)，研制了模型的可视化软件(王丹等，2009； 王仕成等，2007)，方便了模型的利用． WMM2010模型和IGRF11模型在经纬度上均采用1°的分辨率． 从两模型的全球总磁场强度地磁图可以看出，两模型在总体变化趋势上能够很好地吻合，与卫星绘制的地磁图相比也极为相似(由于篇幅所限，未能体现)，并接近于实测值，使其误差控制在较小范围． 综上所述，可以说明两模型的建模过程是正确的，可以提供数值计算和实现模型的可视化． 由于WMM2010在模型实现过程中采用了最新的大量实测数据(海测、 航测和全球提供的最新台测数据)，并且在数据选取和筛选上较IGRF11更为严格，数据处理方法更为科学，更好地剔除了噪声的干扰，在高斯系数拟合过程中使用的数据要远多于IGRF11，因此，在细节刻画上较IGRF11更为精确，反映在总磁场强度等值线图上就是在经纬度和分辨率均相同的条件下，WMM2010在局部区域有明显的锯齿状线条，特别是在梯度变化较大的区域，而IGRF11模型等值线图则表现得比较圆滑． 结合与实测数据的比较，充分说明了WMM2010模型精度要高于IGRF11模型精度．

5.   讨论与结论

本文主要对最新的国际地磁参考场模型IGRF11从建模原理、 数据分析、 误差分析、 模型比较和地磁图对比等方面做了细致的分析． 详尽阐述了建模数据的选取原则、 高斯系数的估算、 数据的校正和模型误差的来源，指出了提高模型精度的困难所在，以及现有模型差异主要集中在对高斯系数的估算上，特别是长期变化系数的估算． 最后通过与实测数据、 WMM2010模型的高斯系数和全球总磁场强度等值线图的比较，得出如下结论： IGRF11的模型计算值与给定的模型检验值的差别很小，误差为十万分之几，充分说明了模型的编程实现过程是正确的，可以提供准确的计算数值； 两种模型在等值线图上的变化趋势可以很好地吻合，各分量要素数值也在合理范围之内，但由于长期变化部分的影响使得两者的数值存在比较大的差异； 由于受地形变化、 测量手段、 测量时间、 静日变化、 外界环境干扰等外部因素的影响，特别是模型没有反映短波长部分及地壳场部分，在精度上与实际磁场还有误差，只能用作参考模型． 使用地磁场模型制备地磁仿真基准图是最有可能和最为便捷的途径，可有效使用国际公开数据，降低攻击路径及目标区地磁图获取难度，减少外场地磁实测工作量和成本，对地磁导航工程化具有重要的价值，但要满足导航方面的需要还存在较大困难． IGRF11模型虽然具有很多优点，特别是在研究地球内部磁流体发电机过程、 区域磁异常、 地磁场长期变化、 地球非偶极子磁场西向漂移、 核幔耦合等方面具有优势，但由于本身长期变化估算时的误差以及只反映了主磁场部分即长波长部分，使得计算的数值与实测值有较大差异，因此，模型的应用范围具有局限性．