引言

目前，地下洞室对弹性波的散射研究多局限在二维模型(Lee，Trifunac,1979; Kobayashi,Nishimura,1983; Manolis,Beskos,1988; Luco，De Barros,1994)． 实际上(地震)波的传播方向与地下洞室轴线多存在一夹角，这时地下洞室对波的散射是一个三维问题． 然而，地下洞室对斜入射平面波三维散射的研究还非常少 (De Barros,Luco,1993; Stamos,Beskos,1996)． 梁建文等(2012)采用间接边界元方法，求解了层状半空间中无限长洞室对斜入射平面SH波的三维散射问题，并通过与已有结果的比较验证了方法的正确性． 本文在梁建文等(2012)方法的基础上，以基岩上单一土层场地为例，研究层状半空间中无限长洞室对斜入射平面SH波三维散射与均匀半空间情况的差别，并分析基岩与土层刚度比、 土层厚度对地表位移幅值的影响． 同时，本文还在频域解答基础上，研究了Ricker波入射下地表位移的时域响应．

1.   频域解答

1.1   基岩与土层刚度比对地表位移幅值的影响

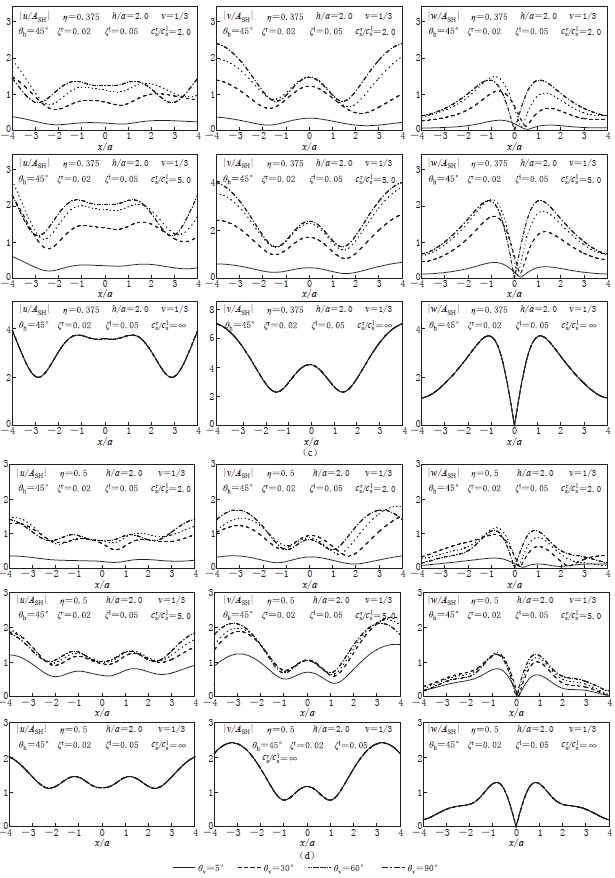
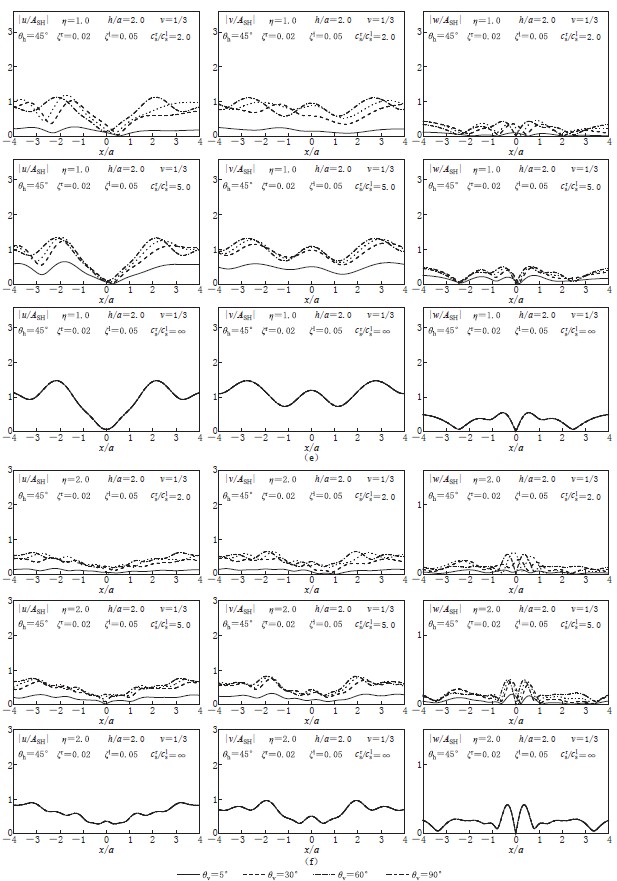
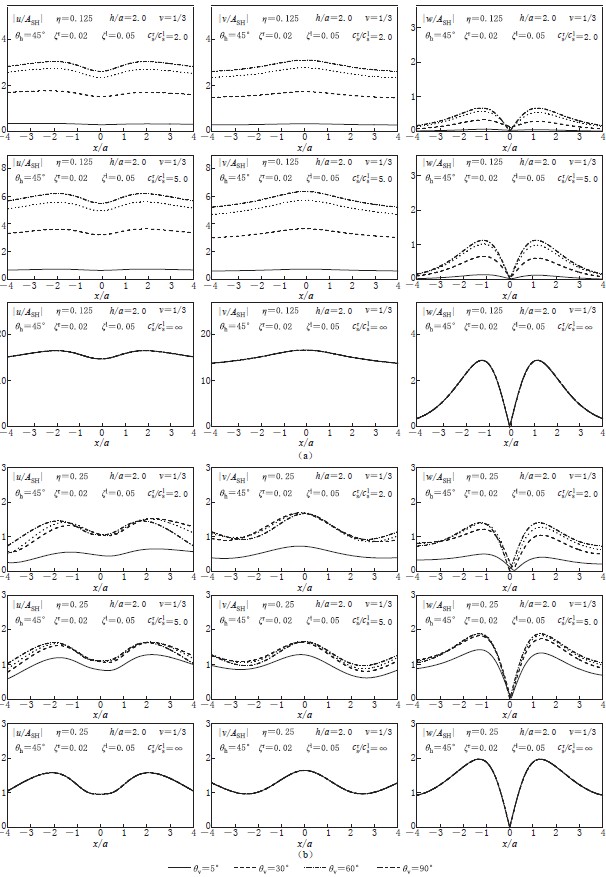
基岩上单一土层场地是最简单的一种层状半空间场地． 图1给出了在平面SH波斜入射下基岩上单一土层场地中圆形洞室附近地表位移幅值． 基岩介质由其剪切波速c^r_s、 质量密度ρ^r、 泊松比ν^r和阻尼比ζ^r确定； 土层由其剪切波速c^l_s、 质量密度ρ^l、 泊松比ν^l和阻尼比ζ^l确定，土层厚度为H． 圆形洞室半径为a，埋深为h． 定义无量纲频率η=ωa/πc^l_s，ω为入射波频率． 计算参数如下： 洞室埋深与洞室半径之比为h/a=2.0，土层厚度与洞室半径之比H/a=4.0，基岩与土层质量密度比ρ^r/ρ^l=1，基岩和土层阻尼分别为ζ^r=0.02和ζ^l=0.05，基岩和土层泊松比为ν^r=ν^l=ν=1/3，波水平入射角度θ_h=45°，竖向入射角度分别为θ_v=5°，30°，60°和90°，波入射频率分别为η=0.125，0.25，0.375，0.5，1.0和2.0． 基岩与土层剪切波速比c^r_s/c^l_s=2.0，5.0和∞． 图1中给出了无量纲地表位移幅值已由基岩面入射SH波位移幅值A_SH正规化．

图  1  基岩与土层刚度比变化对洞室附近地表位移幅值的影响. (a) η=0.125； (b) η=0.25

Figure  1.  Effect of bedrock to soil layer stiffness ratio on surface displacement amplitude near cavity. (a) η=0.125； (b) η=0.25

下载: 全尺寸图片 幻灯片

图  1  基岩与土层刚度比变化对洞室附近地表位移幅值的影响. (a) η=0.375； (b) η=0.5

Figure  1.  Effect of bedrock to soil layer stiffness ratio on surface displacement amplitude near cavity. (a) η=0.375； (b) η=0.5

下载: 全尺寸图片 幻灯片

图  1  基岩与土层刚度比变化对洞室附近地表位移幅值的影响. (a) η=1.0； (b) η=2.0

Figure  1.  Effect of bedrock to soil layer stiffness ratio on surface displacement amplitude near cavity. (a) η=1.0； (b) η=2.0

下载: 全尺寸图片 幻灯片

从图1中可以看出，与均匀半空间情况相比，层状半空间场地由于考虑了土层自身动力特性，洞室附近地表位移幅值存在明显差异． 在土层共振频率附近(η=0.125和η=0.375)时，层状半空间情况地表位移幅值明显大于均匀半空间情况，基岩与土层刚度比的变化也会引起非常大的差别． 如当η=0.125时，c^r_s/c^l_s=∞和c^r_s/c^l_s=5.0情况下两个水平方向地表位移幅值分别达到c^r_s/c^l_s=2.0情况的5倍和2倍． 这是由土层对入射SH波的放大作用引起的．层状半空间情况较均匀半空间情况，地表位移幅值空间分布也更为复杂，这是 因 为层状半空间场地中地表位移幅值是由土层自身动力特性以及洞室对入射SH波的散射二者共同决定的，且洞室与土层之间存在相互作用． 另外，与均匀半空间中洞室在SH波入射时的散射相同，基岩上单一土层中洞室附近（-1≤x/a≤1）地表位移幅值相对较小，而两侧相对较大； 当基岩与土层剪切波速比较小时（c^r_s/c¹_s=2.0），由于洞室对入射平面波存在“屏障效应”，入射波近端地表位移相对比较复杂，而远端地表位移相对比较简单． 对于基岩上单一土层中洞室情况，当波水平入射角度θ_h一定时，随着竖向入射角度θ_v的逐渐增大，地表位移幅值逐渐减小． 这与均匀半空间中洞室情况相反（均匀半空间中，竖向入射角度较小时，地表位移幅值较大）．

从图中还可以看出，随着基岩与土层剪切波速比的不断增大，当竖向入射角度θ_v为5°，30°和60°时，位于洞室上部附近的地表位移幅值变得基本对称，而“屏障效应”变得不再明显． 当c^r_s/c¹_s=∞时，波竖向入射角度虽然改变，但洞室上部附近地表位移幅值相同． 因为对于SH入射，基岩露头只有水平位移，这样当基岩与土层刚度比无穷大时，输入各点的相位相同，所以非垂直角度与垂直角度的输入相同. 而且由于各角度入射时，基岩露头位移幅值一样，因此洞室地表位移幅值与竖向入射角度不再相关．

1.2   土层厚度对地表位移幅值的影响

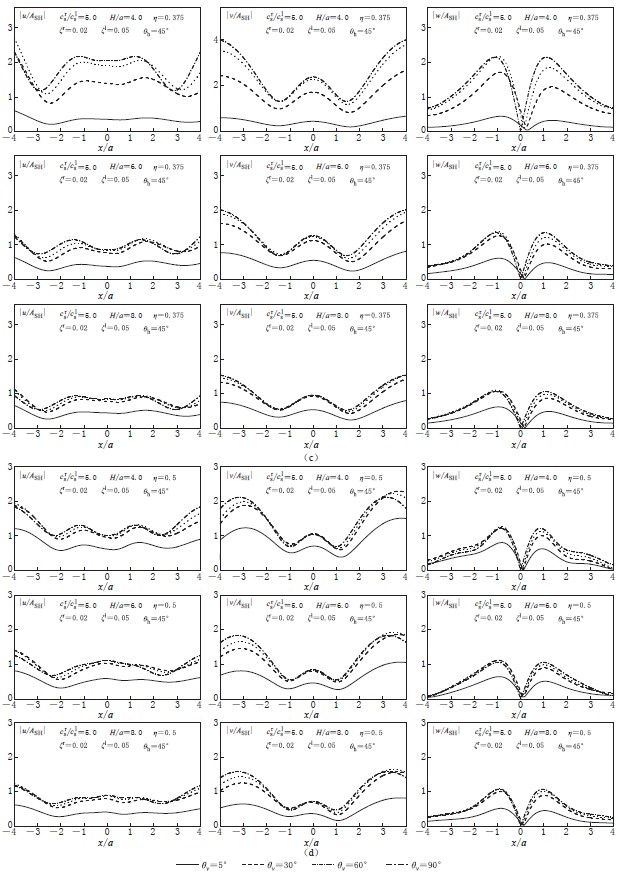
图2给出了土层厚度不同时，洞室附近地表位移幅值． 其它计算参数均与图1中计算参数相同． 入射频率仍为η=0.125,0.25,0.375,0.5,1.0和2.0，基岩与土层剪切波速比c^r_s/c¹_s=5.0，土层厚度分别为H/a=4,6和8．

图  2  土层厚度变化对洞室附近地表位移幅值的影响. (a) η=0.125； (b) η=0.25

Figure  2.  Effect of soil layer thickness on surface displacement amplitude near cavity. (a) η=0.125； (b) η=0.25

下载: 全尺寸图片 幻灯片

图  2  土层厚度变化对洞室附近地表位移幅值的影响. (c) η=0.375； (d) η=0.5

Figure  2.  Effect of soil layer thickness on surface displacement amplitude near cavity. (c) η=0.375； (d) η=0.5

下载: 全尺寸图片 幻灯片

从图2中可以看出，土层厚度的改变对地表位移幅值有着显著的影响． 随着土层厚度的增大，整体上地表位移幅值逐渐减小． 这是因为本文考虑了土层和基岩的材料阻尼，故随着土层厚度的增大，位移幅值衰减越多． 可以预计，随着土层厚度的逐渐增大，地表位移幅值会逐渐趋近于均匀半空间情况． 但值得指出的是，当波入射频率与土层共振频率相同或比较接近时，会出现例外． 例如当η=0.25、 H/a=6时，地表位移幅值会大于H/a=4时地表位移幅值，因为H/a=6正好位于土层第二共振频率． 另外，由于考虑了土层和基岩的材料阻尼，随着入射频率的增大，地表位移幅值会逐渐减小． 例如当土层厚度H/a=8、 入射频率η=2.0时，地表位移幅值会非常小． 从图中还可以看出，当入射频率较低时（如η=0.125），地表位移幅值趋近于均匀半空间中自由场位移幅值. 说明当入射频率很小时，入射波不仅感觉不到洞室的存在，也感觉不到土层的存在．

2.   时域解答

为了清晰地说明斜入射平面SH波在层状半空间中的传播以及在洞室周围散射的过程，图3给出了均匀半空间和基岩上单一土层中洞室在Ricker波入射下地表位移． Ricker波在地震学中常用来分析研究波的时域散射规律，其形式为

式中，f_C=fa/c¹_s为特征频率，τ=tc¹_s/a为无量纲时间． 计算参数： 洞室埋深与洞室半径之比为h/a=2.0，土层厚度与洞室半径之比分别为H/a=4.0和8.0，基岩与土层的剪切波速比分别为c^r_s/c¹_s=2.0和c^r_s/c¹_s=5.0，基岩与土层质量密度比ρ^r/ρ¹=1，基岩和土层泊松比ν^r=ν¹=1/3，基岩阻尼比ζ^r=0.02，土层阻尼比ζ¹=0.05，波垂直入射角度=45°，水平入射角度=45°，特征频率f_c=1.0．

具体计算时，首先把Ricker波时程通过傅里叶分析变换到频域，然后针对每个频率，按照前述频域计算方法，在频域内进行计算，最后通过傅里叶逆变换得到时域结果． 文中波的输入位置均选在基岩露头处．

首先考察均匀半空间情况（图3a）． 从图中可以看出，由于洞室对波的屏障效应，入射端地表位移比较复杂，波动的持续时间比较长； 远端地表位移相对简单，波动的持续时间相对较短． 两个水平方向波的传播同步，但入射端与远端之间延迟非常明显； 而竖向总体到时相对较晚，且波最先到达洞室上方. 这是因为竖向地表位移是由波的散射引起的，洞室上方地表距离洞室最近，因此波最先到达．

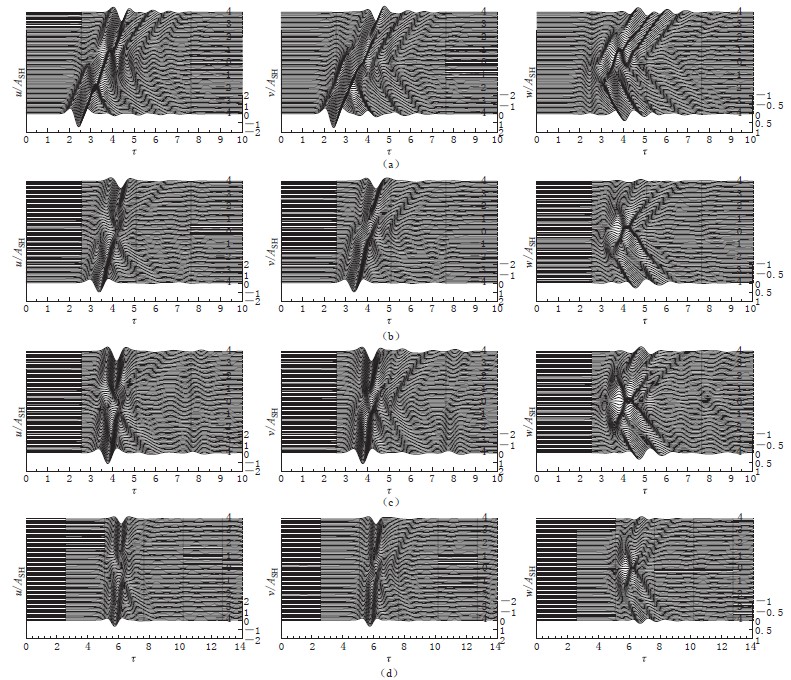
图  3  时域内洞室附近地表位移 (a) 均匀半空间； (b) 基岩上单一土层(c^r_s/c^l_s=2.0，H/a=4.0)；(c) 基岩上单一土层(c^r_s/c^l_s=5.0，H/a=4.0)；(d) 基岩上单一土层(c^r_s/c^l_s=5.0，H/a=8.0)

Figure  3.  Time-domain surface displacementnear cavity (a) Homogeneous half-space； (b) Single layer over bedrock (c^r_s/c^l_s=2.0，H/a=4.0)； (c) Single layer over bedrock (c^r_s/c^l_s=5.0，H/a=4.0)；(d) Single layer over bedrock (c^r_s/c^l_s=5.0，H/a=8.0)

下载: 全尺寸图片 幻灯片

下面考察层状半空间情况(图3b-d)． 从图中可以看出，洞室对波的屏障效应相对于均匀半空间情况有所减弱，两个水平方向波的到达延时相对于均匀半空间情况也有所缩短，其原因是波由基岩折射到土层时，波的入射角度增大所致.随着基岩与土层刚度比的增大，地表位移逐渐增大，两个水平方向波的到达延时进一步缩短． 这是因为波的入射角度随基岩与土层刚度比的增大而增大． 随着土层厚度的增加，地表位移逐渐减小，总体到时逐渐延长． 这是由于阻尼的原因，波的传播路径的增加，会导致波的进一步衰减、 总体到时进一步延长．

3.   结论

本文通过数值计算研究了层状半空间中无限长洞室对斜入射平面SH波的散射问题，以基岩上单一土层场地为例研究了基岩与土层刚度比、 土层厚度等对散射的影响． 研究表明，层状半空间中洞室对斜入射平面SH波的散射与均匀半空间中洞室对斜入射SH波的散射存在显著差别． 由于土层和洞室对斜入射平面SH的共同作用，层状半空间中地表位移幅值空间、 时间变化都较均匀半空间中情况要复杂． 基岩与土层刚度比和土层厚度对地表位移幅值均有着重要的影响： 随着基岩与土层刚度比的增大，地表位移幅值整体上逐渐增大，基岩与土层刚度比无穷情况下地表位移幅值可以达到基岩与土层刚度比两倍情况的5倍； 随着土层厚度的增大，土层对地表位移幅值的影响逐渐减小，且可以预计，地表位移幅值会逐渐趋近于均匀半空间情况． 层状半空间中无限长洞室对斜入射平面SH波散射的时域响应与频域响应有着相似的规律．