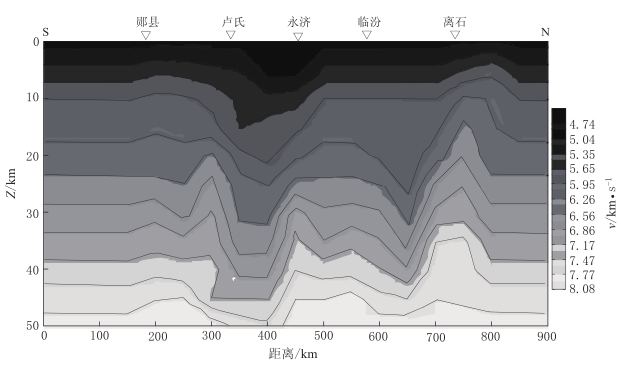
Crustal P-wave velocity beneath the Loess Plateau and its surrounding region
-
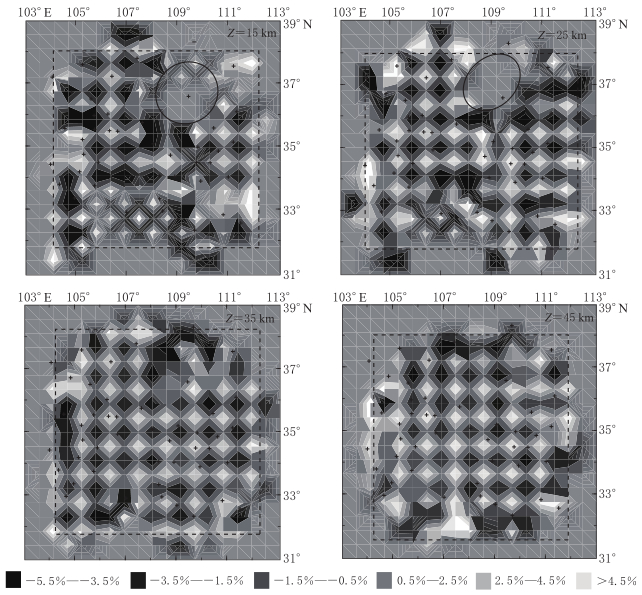
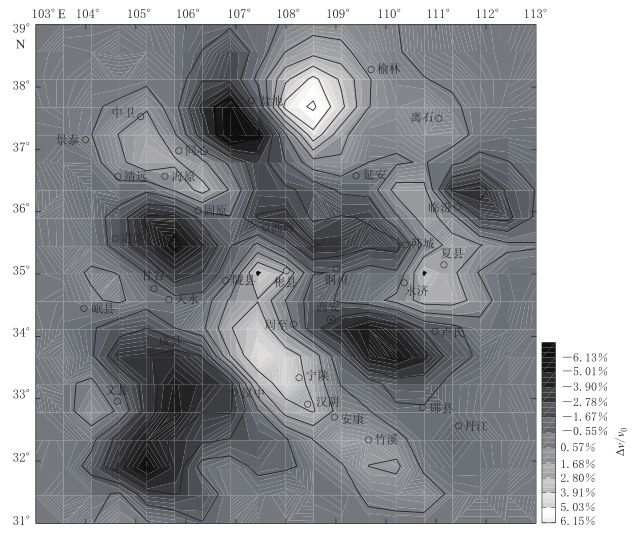
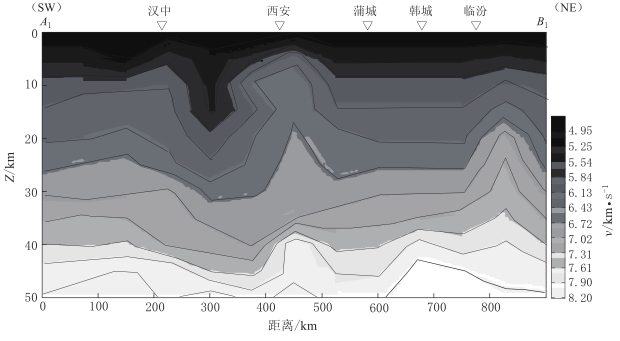
摘要: 利用地震波走时联合反演算法(改进型最短路径算法)进行三维弯曲地震射线追踪正演, 以及共轭梯度法求解带约束的阻尼最小二乘问题进行反演， 同时更新速度模型和地震震中位置, 结合地方震和区域地震走时资料得到了黄土高原(含汾渭断陷盆地)及邻区地壳三维P波速度结构. 其横向变化结果表明, 研究区地壳内的P波高速异常区与其内的地震活动构造带相一致, 地震多发生在P波高速异常区的边缘或高、 低速异常区的交汇处. 秦岭山区和鄂尔多斯块体东南区为P波低速异常区. 而垂向变化结果则表明研究区存在低速异常区.Abstract: A simultaneous travel time inversion procedure was developed in collaboration with a modified shortest path algorithm, which was applied to a bent ray tracing forward calculation. The conjugate gradient algorithm was used to solve a damped least square problem. The crustal P-wave velocity structure beneath the Loess Plateau and its surrounding regions of China were tomographically imagined down to the depth of 50 km by inverting P wave travel time data from local and regional earthquakes. The result indicates that lateral high velocity anomaly regions generally coincide with the seismically active zones, while vertical velocity variations show existence of a low velocity zone.
-
引言
完整的地震目录对强震预测和地震学的研究有着重要的意义．人工地震、 矿山爆破等有着类似于天然地震的波形记录，如果不能及时剔除，会混淆地震目录，影响日后地震学的研究． 目前由于经济建设的快速发展，小当量爆破事件日益增多，增大了天然地震与非天然地震识别的难度； 科学技术的发展以及全面禁止核试验条约的实施，用以逃避核查的小当量核试验具有更大的隐蔽性，而且由于地震监测网的建设受各国敏感区域保护的限制，小当量地下核爆炸的识别也是军控核查中的难点问题． 因此小震级天然地震与人工爆破的识别是非常重要的．
识别天然地震与人工爆破的判据很多，如震源位置、 震源深度、 P波初动、 P波和S波最大振幅比、 体波震级与面波震级比、 倒谱、 瞬态谱等(沈萍，郑治真，1999； 魏富胜，黎明，2003； 边银菊，2005； 王婷婷，边银菊，2011)． 近年来P/S震相幅值比是研究最为深入的一个判别量，可分为同一频段内P波和S波震相幅值比、 同一震相低频与高频幅值比、 不同震相高频与低频幅值比等． Shin等(2010)分析了2009年朝鲜第二次核爆与附近的两次地震垂直向记录在0.5—15 Hz之间的Pn/Lg比值，得到大于4 Hz时可将两类事件完全分别出来． Chun等(2011)分析了不同台站记录到的朝鲜2006年和2009年两次核爆与中朝边界的地震，定义P/S比值为(PZ2+ PR2)1/2/(SZ2+SR2+ST2)1/2，得到3—11 Hz内地震与核爆识别效果好． 也有研究将不同频段的P/S震相幅值比相结合或用震级和距离校正方法(magnitude and distance amplitude correction，简称为MDAC)来提高识别能力(Taylor et al，2002; Walter et al，2005； Che et al，2007； 潘常周等，2007; Fisk et al，2009; Pasyanos，Walter，2009; Hong，Rhie，2009； Pasyanos，2010; Taylor，2011)． 上述研究结果均表明，P/S判别量在地震与爆破识别中效果较好且对频率的依赖性较大，即爆破与地震的频率成分有差异，因此，对地震与爆破记录划分不同频段进行研究是非常有必要的．
杨选辉等(2005)将小波包分量比方法引入乌鲁木齐台的地震与核爆识别中．结果表明，对于地震信号，其小波包分量比U30/U31一般都大于1.0； 而对于核爆信号，其比值一般都小于1.0．和雪松等(2006)用小波包将信号变换到频域，再用奇异值分解作为统计工具，提取天然地震和矿震的识别因子． 曾宪伟等(2010)采用demy小波函数对银川地震台记录到的14次地震和19次爆破事件进行5层小波包变换，并通过比较地震信号与爆破信号的P波段时频谱值及S波段时频谱值达到最大时的频率差异，寻找合适的单项定量识别指标，并综合各单项识别指标形成综合识别判据． 但是迄今为止几乎所有关于P/S震相比值大部分是针对较大震级．本文主要针对小震级地震和爆破，用小波包分解来分析P波和S波在各频段的差异，并提取识别率较好的识别特征．
1. 小波包分析
小波分析被认为是傅里叶分析方法的突破性进展，作为一种技术工具和方法，离散小波变换在各个领域，如信号信息处理、 图像处理、 语言分析等都得到很好的应用． 在地球物理信号处理方面也展现出广泛的应用前景． 例如，将小波变换用于地震波形反演、 石油勘探中的地层吸收、 重力异常多重分解等． 小波分析中常用Mallat二进小波算法，在二进小波分析中，信号在频率域按二分法向低频方向进行分解． 而小波包方法则是小波变换的扩展，不仅对信号的低频部分进行分解，还对高频部分以二进方式分解，可将信号的频段分得更加精细，提高了信号在整个频带内的分辨能力，这样可以了解信号中包含的更多细节信息．
定义子空间Ujn是函数un(t)的闭包空间，而Uj2n是函数u2n(t)的闭包空间，并令un(t)满足下面的双尺度方程：
式中，g(k)=(-1)kh(1-k)，即两系数具有正交关系． 当n=0时，式(1)给出
式中，φ(t)和ψ(t)分别为多分辨分析中的尺度函数与小波基函数，我们称由式(1)构造的序列{un(t)}(其中n∈Z+)为由基函数u0(t)=φ(t)确定的正交小波包． 当n=0时即为式(2)的情况(胡昌华等，2000； 黄汉明等，2010)． 信号的4层分解示意图(图 1)，对信号(以[0，0]表示)，我们可将它分解为低频节点[1，0]和高频节点[1，1]，然后将低频节点[1，0]进一步分解为低频节点[2，0]和高频节点[2，1]，同时对高频节点[1，1]也继续分解为低频节点[2，2]和高频节点[2，3]. 以此类推，随着分解尺度的增加，信号在整个频带内分解得更细．如果对信号进行m层小波包分解，则可得到2m个分解信号． 本文为了获取精细的频率成分，用sym5小波基函数对信号进行4层小波包分解，得到24即16个节点 [4，0]，[4，1]，…，[4，15] 的信号．
![]()
图 1 小波包变换4层分解及对应频段示意图Figure 1. Schema of four-layer wavelet packet decomposition and corresponding frequency bands参考曾宪伟等(2008)给出的小波包分解后节点与频带对应图，我们绘制了采样率为50点/秒的信号节点与频带对应关系，如图 1所示． 其中，HP表示高通滤波器，LP表示低通滤波器． 为了进一步验证节点与频带对应顺序，我们用sym5小波包基函数对实际地震信号进行4层小波包分解，并分别绘制了按节点顺序和频带顺序的排列结果(图 2)． 从图 2中可看出，小波包分解后按频段排列的节点顺序与图 1相同．
![]()
图 2 小波包第4层分解的两种排序对比 (a) 按节点顺序排序； (b) 按频段顺序排序(a) 按节点顺序排序； (b) 按频段顺序排序Figure 2. Comparison of thefourth-layer wavelet packet decomposition sorted by node order (a) and by frequency band order (b)2. 资料选取
本文选取了北京及其邻近地区的29次爆破(2002—2010年，ML1.0—2.5)和33次地震(2003—2007年，ML1.3—3.2)，共62个事件． 事件的地理范围为39.5°—40.6°N，115.0°—116.5°E． 选取记录波形较好的台站，共59个，所选事件及台站分布如图 3所示． 经分析记录波形发现，XBZ台站是所选台站中对62个事件记录较齐全的一个台站，共记录到波形较好的爆破有20次，地震27次． 全文主要对XBZ台站记录的波形进行小波包分析，因此对XBZ台站记录到的20次爆破和27次地震分别按发震时间顺序进行编号．
![]()
图 3 事件及记录台站位置示意图红色圆圈表示爆破， 粉色星号表示地震， 黑色三角表示台站， 蓝色三角为XBZ台站Figure 3. Location of events and recording stations in this studyRed circles denote explosions, pink asterisks denote earthquakes, black triangles denote stations, blue triangle is XBZ station3. 利用小波包提取判据
3.1 记录的小波包变换
XBZ台站是宽频带记录仪，采样率是50点/秒，波形记录的频率范围是0—25 Hz． 对所有垂直向宽频带记录，取完全包含P波、 S波组在内的1000个点采用小波基函数sym5进行4层小波包分解，用小波包系数重构得到16个节点 [4，0]，[4，1]，…，[4，15] 的信号． 计算各节点(频段)能量谱与总能量之比，即进行时频谱归一化． 图 4所示为XBZ台站记录到的2002年5月21日震级为ML1.1爆破和2004年1月26日震级为ML1.5地震垂直向归一化记录及时频谱图(震中距分别为45.6 km和39.1 km)，其中频率轴采用各频段的中心频率． 经分析20次爆破和27次地震时频谱图可得出：
![]()
图 4 事件波形及时频谱图(粉色段表示P波， 黑色段表示S波)(a) 人工爆破波形及时频谱图； (b) 天然地震波形及时频谱图Figure 4. Event waveforms and their spectrograms in which the pink segment represents P wave and the black segment represents S wave(a) Explosion waveform and spectrogram; (b) Earthquake waveform and spectrogram1)爆破频谱简单，P波段能量高于S波段； 地震则相反．
2)爆破P波段能量集中在几个频带区内，主要集中在节点[4，2]，[4，3]，[4，6]和[4，7]处，主频频率在9.375 Hz以内； S波段能量所在频率也较低，时频谱相对地震来说聚集性较好．
3)地震的P波、 S波段频率均较复杂，尤其是S波段频率成分丰富，并含有一些高频成分．
对XBZ台站记录的27次地震和20次爆破垂直向选取P波、 S波各128个点，采用小波包基函数sym5做4层小波包分解，并对第4层分解得到16个节点[4，0]，[4，1]，…，[4，15]，用小波包变换系数重构出各节点的信号． 定义各节点信号的平方和为该频段信号的能量(E)，公式为
式中，N为各节点(频段)系数的点数，fi为该频段内的信号． 图 5所示为XBZ台站记录的2002年5月21日爆破P波段128个点及其第4层小波包分解的各节点信号．
![]()
图 5 2002年5月21日爆破P波段的第4层小波包分解Figure 5. The fourth-layer wavelet packet decomposition of explosion P wave on 21 May 20023.2 能量比判据定义
1)P/S能量比判据．对同一事件XBZ台站记录到的垂直向波形选取P波段128个数据点和S波段128个数据点，采用小波基函数sym5作小波包变换，分解层数为4层． 用小波包系数重构出各节点信号，依照式(3)所定义的方法求出各节点(即各频段)的能量． 依次用P波各节点的能量值与S波各节点的能量值相比，求取对数结果． 第4层P波段有16个节点，S波段有16个节点，共有256个比值结果： EPS([4，0]/[4，0])，EPS([4，0]/[4，1])，…，EPS([4，15]/[4，15])． 其中每一个能量比值结果作为一个判据，则对每一事件可以提取256个判据．
2)其它能量比判据．考虑到波形记录不全等问题，有些波形只记录到P波，有些只记录到S波的情况，我们也分析了P波能量比判据和S波能量比判据，作为小波包能量比判据研究的补充．
用sym5小波包基函数对47个事件P波段128个数据点做4层小波包分解，并重构出各节点信号． 依照式(3)所定义的方法求出P波段各节点(即各频段)的能量，依次求出P波各节点能量比值的对数结果，由此得到一系列判据． 第4层共有16个节点，则有120个P波能量比判据： EPP([4，0]/[4，1])，EPP([4，0]/[4，2])，…，EPP([4，14]/[4，15])． 同样的定义及方法求出120个S波能量比判据： ESS([4，0]/[4，1])，ESS([4，0]/[4，2])，…，ESS([4，14]/[4，15])．
4. 判据分析
4.1 P/S能量比判据结果分析
1)P/S能量比判据识别结果．依照P/S能量比判据的定义，每个事件得到256个P/S能量比判据值． 对47个事件绘制每个判据的判据分布图，观察地震与爆破判据值的分布情况，并找出最佳阈值． 经研究得到256个能量比判据中正确识别率达到90%以上的有75个，比值结果均是爆破大于地震． 其中正确识别率在95%以上的P/S能量比判据共37个． 可以将地震与爆破完全分开的P/S能量比判据有9个： EPS([4，2]/[4，14])，EPS([4，2]/[4，15])，EPS([4，3]/[4，15])，EPS([4，5]/[4，15])，EPS([4，6]/[4，4])，EPS([4，6]/[4，15])，EPS([4，7]/[4，9])，EPS([4，7]/[4，10])，EPS([4，7]/[4，15])．
2)P/S能量比判据的检验结果．① C检验结果． C检验方法是将全部样品用于学习或训练，并用相同的样品进行检验，因此P/S能量比判据的识别结果，也即是C方法的检验结果． ② U检验结果．U检验方法是将N个样品中前n个进行学习，后N-n个进行检验(王碧泉，陈祖萌，1989)． 我们选用前18次地震和前14次爆破作为训练集，剩余的9次地震和6次爆破来做识别检验． 256个P/S能量比判据中正确识别率在90%以上的判据有64个． 其中正确识别率达100%的P/S能量比判据有26个．
3)P/S能量比识别判据选取．本文认为C检验结果正确识别率在95%以上，同时U检验结果的正确识别率在90%以上的P/S能量比判据识别效果较好，可在实际问题中应用． 经统计达到要求的P/S能量比判据共35个，其中有9个能量比判据可以将地震与爆破完全区分开，其C检验与U检验的正确识别率均为100%，如表 1所示．
表 1 P/S能量比判据的识别结果和检验结果Table 1. The recognition and test results of P/S energy ratios
对识别效果较好的35个P/S能量比判据分析如下：
1)这35个P/S能量比判据C检验结果的正确识别率在95%以上，U检验结果识别率在90%以上，表明P/S能量比判据可以较好地识别本文所研究地区的地震与爆破，而且识别效果稳定． 从判据中节点出现的次数来看，P波节点主要集中在[4，2]，[4，3]，[4，6]和[4，7]，主频所对应的频段是3.125—9.375 Hz； S波节点主要集中在节点[4，9]—[4，15]，各节点主频对应的频段为12.5—23.4375 Hz． 在这些频段上，爆破事件的P波与S波差异要大于地震事件的P波与S波差异． 结合时频谱图得到的结果可认为，爆破的P波在节点[4，2]，[4，3]，[4，6]和[4，7]处能量较多，而地震的S波在12.5 Hz以后也发育，因此爆破的低频P波与高频S波能量比值大于地震．
2)正确识别率达100%的判据有9个(表 1)． 进一步表明使用P/S能量比判据识别效果好． 9个判据中有8个是爆破低频P波与高频S波的差异大于地震． 另一个判据EPS([4，6]/[4，4])，与文中时频谱图得出的爆破P波主要能量集中在节点[4，6]和[4，7]处结果一致．
图 6为正确识别率达100%的判据值EPS([4，2]/[4，15])，EPS([4，6]/[4，15])的C检验及U检验结果． 从图 6中可看出，判据P/S比值爆破大于地震，说明爆破P波与S波的频率差异比地震大．
![]()
图 6 P/S能量比判据值分布(a) EPS([4, 2]/[4, 15])判据识别结果；(b) EPS([4, 6]/ [4, 15])判据识别结果； (c) EPS([4, 2]/[4, 15]) 判据U检验结果； (d) EPS([4, 6]/ [4, 15])判据U检验结果． 空心圆圈表示爆破， 空心三角表示地震， 黑色线段表示阈值， 实心圆与实心三角分别表示U检验中用于测试的爆破与地震Figure 6. Distribution of P/S energy ratio criterion values(a) The recognition results of EPS([4, 2]/[4, 15]) criterion; (b) The recognition results of EPS ([4, 6]/[4, 15]) criterion;(c) The U-test results of EPS([4, 2]/[4, 15]) criterion; (d) The U-test results of EPS ([4, 6]/[4, 15]) criterion. The open circles denote explosions, the open triangles denote earthquakes, solid line shows threshold value, the solid circles and triangles denote test explosions and earthquakes for U-test4.2 其它能量比判据结果分析
考虑到波形记录不全等问题，我们也提取了P波能量比判据和S波能量比判据．
4.2.1 P波能量比判据选取
依照P波能量比判据的定义，每个事件得到120个P波能量比判据值． 绘制判据分布图，并找出最佳阈值尽量将地震与爆破分开． 经研究得到120个P波能量比判据识别中正确识别率大于90% 的有8个判据，也即这8个P波能量比判据的C检验结果识别率大于90%，比值结果均为爆破P波能量比大于地震P波能量比； U检验结果正确识别率大于90%的有13个． 我们认为C检验结果与U检验结果识别率同时大于90%的判据为P波能量比较好的判据，可在实际中应用． 经统计C检验结果与U检验结果识别率均大于90%的判据共有5个，如表 2所示．
表 2 选取的P波能量比判据的识别结果和检验结果Table 2. The recognition and test results of selected P wave energy ratio criteria
对所选取的P波能量比判据(表 2)分析如下：
1)对于P波能量比判据，识别较好的判据共有5个，可认为单独使用P波能量比要比综合使用P/S能量比结果差． 从P波能量比较好的判据中节点出现次数来看，判据比值分子为[4，2]和[4，7]，各节点主频对应的频段为4.6875—6.25 Hz和7.8125—9.375 Hz，也进一步支持了时频谱图与P/S能量比所得到的爆破P波在节点[4，2]，[4，3]，[4，6]和[4，7]处能量较多的结论．
2)U检验结果中出现3个正确识别率为100%的情况，识别效果比C检验结果好. 这可能与本文选取训练集和测试集方法的原因有关，若是随机选取训练集，并用剩余的作为测试样本，这种情况出现概率可能较小．
3)5个判据中EPP([4，7]/[4，9])识别效果最好，C检验结果仅识别错误一次地震和一次爆破，正确识别率为96%； U检验结果的正确识别率达100%． 绘制地震与爆破EPP([4，7]/[4，9])判据的识别结果(即C检验结果)和U检验结果如图 7所示．
![]()
图 7 P波能量比判据值分布(a) EPP([4, 7]/ [4, 9])判据识别结果(C检验结果)； (b) EPP([4, 7]/ [4, 9])判据U检验结果 空心圆圈表示爆破， 空心三角表示地震， 黑色线段表示阈值， 实心圆与实心三角 分别表示U检验中用于测试的爆破与地震Figure 7. Distribution of P wave energy ratio criterion values(a) The recognition results of EPP ([4, 7]/[4, 9]) criterion; (b) The U-test results of EPP([4, 7]/[4, 9]) criterion. The open circles denote explosions, the open triangles denote earthquakes, solid line shows threshold value, the solid circles and triangles denote test explosions and earthquakes for U-test4.2.2 S波能量比判据选取
与P波能量比判据的分析类似，我们选取C检验与U检验结果同时大于90%的判据为S波能量比识别较好的判据，共15个可在实际中应用．
经分析15个S波能量比判据发现，均是爆破S波段的低频与高频能量比值大于地震，表明爆破的S波在低频与高频处的差异大于地震． 其中多数低频节点分布在[4，0]，[4，1]和[4，3]，主频所对应的频率在4.6875 Hz以内，多数高频节点是[4，13]，[4，14]和[4，15]，所对应的频率段大于14 Hz． 这一结果也支持了时频谱图与P/S能量比所得到的地震S波在12.5 Hz以后较发育的结论． 15个判据中ESS([4，0]/[4，15])的识别效果较好，C检验结果识别错误2次地震，正确识别率为96%； U检验结果的正确识别率达100%． 绘制ESS([4，0]/[4，15])判据识别结果(即C检验结果)和U检验结果如图 8所示．
![]()
图 8 S波能量比判据值分布(a) ESS([4, 0]/[4, 15])判据识别结果(C检验结果)； (b) ESS([4, 0]/[4, 15])判据U检验结果 空心圆圈表示爆破， 空心三角表示地震， 黑色线段表示阈值， 实心圆与实心三角分别 表示U检验中用于测试的爆破与地震Figure 8. Distribution of S wave energy ratio criterion values(a) The recognition results of ESS ([4, 0]/[4, 15]) criterion; (b) The U-test results of ESS ([4, 0]/[4, 15]) criterion． The open circles denote explosions, the open triangles denote earthquakes, solid line shows threshold value, the solid circles and triangles denote test explosions and earthquakes for U-test4.3 能量比判据的物理解释
地震是由岩石破裂错动而产生，一般震源深度较爆破深，地震波的传播路径经过多层介质的反射和折射，因此台站记录到地震波的成分比较丰富，波的频带范围也比较宽； 而爆破源体积较小，可以认为是瞬间的膨胀源，而且多发生在地表，波的传播路径较简单，信号频带范围较窄． 一般认为地震的能量释放相对爆破要缓慢一些，所以地震能量信号集中于低频段，爆破能量多集中于高频段． 然而，爆破信号的一个特点是距离爆源较近时地震波的高频成分丰富，且持续时间短，但爆破信号在传播过程中有较长的路程在较为松散的浅层，因此远距离的高频成分衰减非常快，低频成分相对增大(曾宪伟，2008)．
对于本文研究的爆破区域处于首都圈西部山区，爆破震源浅，在传播中受路径影响较大，经过松散地层，波的高频成分被吸收的多． 小波包分解结果表明，地震波频率成分较复杂，爆破频率成分简单，时频谱相对地震来说聚集性较好． 正确识别率在95%以上的低频P波能量与高频S波能量之比均是爆破大于地震，表明爆破的P波能量在某些频段内发育，而地震的S波能量在高频处较爆破发育． 此处所谓的高频成分P波与S波均指在12.5 Hz以上．
5. 结论
本文利用小波包基函数sym5对XBZ台站记录到的20次爆破和27次地震垂直向波形记录做4层小波包分解并绘制时频谱图，分析波形的频率成分，定义并提取了P/S能量比判据256个． 本文认为较好的P/S能量判据要满足C检验正确识别率在95%以上，且U检验正确识别率在90%以上，经统计达到要求的P/S能量比判据共35个． 作为小波包判据研究的补充，也提取了P波能量比判据和S波能量比判据，具体分析了C检验和U检验正确识别率同时大于90%的5个P波能量比判据和15个S波能量比判据． 通过分析频谱图和能量比判据本文得到以下结论：
1)本文将小波包变换用于地震与爆破的识别，提出并定义了P/S能量比、 P波能量比和S波能量比判据． 结果表明能量比识别效果较好，本文优先推荐9个正确识别率为100%的P/S能量比判据在实际中应用．
2)从时频谱图可直观看出，爆破频率成分简单，时频谱相对地震来说聚集性较好，P波段频率在10 Hz以内； 而地震的P波、 S波段频率均较复杂，尤其是S波段频谱丰富，与爆破相比含有较多的高频成分．
3)分析识别效果较好的35个P/S能量比判据，得出P波主要集中在[4，2]，[4，3]，[4，6]和[4，7]，主频所对应的频段是3.125—9.375 Hz； S波主要集中在节点[4，9]—[4，15]，对应的频段在12.5—23.4375 Hz． 表明在这些频段上，爆破事件的P波与S波差异要大于地震事件的P波与S波差异． P波能量比和S波能量比判据结果得出，爆破P波在节点[4，2]和[4，7]内能量多于其它频段，S波的低频与高频能量比值大于地震．
4)文中爆破相对于台站位置单一，而地震分布在台站的各个角度，有一定的普适性. 但由于爆破方式、 传播路径等影响，并不适合所有地点的地震与爆破识别． 因此我们将进一步研究不同地点的爆破，选择不同方位的台站记录进行小波包分析，而且需要更多的样本，以此来提高地震与爆破识别的普遍实用性．
-
![]()
图 1 研究区基本构造示意图
实线表示活动断层; 虚线表示不活动断层
Figure 1. Basic tectonic structure of the study region
Solid lines show active faults,dash lines denote inactive faults
![]()
图 2 地震(实心圆)、 台站(十字)及随后展示剖面(虚线)分布图
Figure 2. Distribution of earthquakes (solid circles) and stations (crosses).Dash lines show position of vertical profiles analyzed in the following
![]()
图 3 检测板试验. 十字表示台站; 虚线矩形表示最佳分辨区; 实线椭圆表示分辨空区
Figure 3. Checkerboard test result. Crosses stand for stations; dash square represents best resolution area; ellipse stands for a resolution gap
![]()
图 4 原始数据时距曲线(a)和用Wiechert-Herglotz方法得到的一维速度模型(b)
Figure 4. Raw time-distance curve for P-wave arrivals (a) and the deduced 1-D velocity model from relocated dataset,which was used as the initial model in the following 3-D inversion (b)
![]()
图 5 P波速度在Z=5 km水平面上相对于背景值的百分比变化空心圆表示台站所在地; 实线表示速度等值线; Δv/v0表示速度扰动
Figure 5. The percentage P-wave variation against the background velocity at the depth of 5 kmOpen circles represent stations; dash lines stand for equal velocity contours; Δv/v0 represents velocity perturbation
![]()
图 6 P波速度在Z=20 km平面上相对于背景值的百分比变化空心圆表示台站所在地; 实线表示速度等值线; Δv/v0表示速度扰动
Figure 6. The percentage P-wave variation against the background velocity at depth of 20 kmOpen circles represent stations; dash lines stand for equal velocity contousr; Δv/v0 represents velocity perturbation
![]()
图 7 P波速度在Z=30 km平面上相对于背景值的百分比变化空心圆表示台站所在地; 实线表示速度等值线; Δv/v0表示速度扰动
Figure 7. The percentage P-wave variation against the background velocity at depth of 30 kmOpen circles represent stations; dash lines stand for equal velocity contours; Δv/v0 represents velocity perturbation
![]()
图 8 P波速度在Z=45 km平面相对于背景值的百分比变化空心圆表示台站所在地; 实线表示速度等值线; Δv/v0: 速度扰动
Figure 8. The percentage P-wave variation against the background velocity at depth of 45 kmOpen circles represent stations; dash lines stand for equal velocity contours; Δv/v0 represents velocity perturbation
![]()
图 9 沿汾渭断裂带走向垂直剖面P波速度分布(图中附有速度等值线)
Figure 9. P-wave velocity vertical profile along the Fenwei belt. Lines represent equal velocity contours
![]()
图 10 垂直汾渭断裂带走向垂直剖面P波速度分布(图中附有速度等值线)
Figure 10. P-wave velocity vertical profile perpendicular to the Fenwei belt. Lines represent equal velocity contours
![]()
图 11 沿纬向(纬度为33.9°)垂直剖面P波速度分布(图中附有速度等值线)
Figure 11. Vertical profile of P-wave velocity map along the latitude of 33.9°. Lines represent equal velocity contours
-
白超英, 秦保燕. 1990. 深部剪切形变带对浅源地震的控制-立交模式有限元的模拟计算[J]. 西北地震学报, 12(1): 1-11. 陈九辉, 刘启元, 李顺成, 郭飙, 赖院根. 2005. 青藏高原东北缘-鄂尔多斯地块地壳上地幔S波速度结构[J]. 地球物理学报, 48(2): 333-342. 丁韫玉, 狄秀岭, 袁志祥, 薛广盈. 2000. 渭河断陷地壳三维S波速度结构和vP/vS分布图像[J]. 地球物理学报, 43(2): 194-202. 嘉世旭, 张先康. 2005. 华北不同构造块体地壳结构及其对比研究[J]. 地球物理学报, 48(3): 611-620. 江为为, 郝天珧, 胥颐, 刘振峰, 朱东英, 涂广红. 2007. 中国中南地区综合地质地球物理研究[J]. 地球物理学报, 50(1): 171-183. 雷建设, 周蕙兰, 赵大鹏. 2002. 帕米尔及邻区地壳上地幔P波三维速度结构的研究[J]. 地球物理学报, 45(6): 802-811. 吕作勇, 吴建平. 2010. 华北地区地壳上地幔三维P波速度结构[J]. 地震学报, 32(1): 1-11. 郭飚, 刘启元, 陈九辉, 赵大鹏, 李顺成, 赖院根. 2004. 青藏高原东北缘-鄂尔多斯地壳上地幔地震层析成像研究[J]. 地球物理学报, 47(5): 790-797. 唐小平, 白超英. 2009a. 最短路径算法下三维层状介质中多次波追踪[J]. 地球物理学报, 52(10): 2635-2643. 唐小平, 白超英. 2009b. 最短路径算法下二维层状介质中多次波追踪[J]. 地球物理学进展, 24(6): 2087-2096. 王志铄, 王椿镛, 曾融生, 王溪莉. 2008. 华北及邻区地壳上地幔三维速度结构的地震走时层析成像[J]. CT理论与应用研究, 17(2): 15-27. 曾融生, 丁志峰, 吴庆举. 1998. 喜马拉雅-祁连山地壳构造与大陆-大陆碰撞过程[J]. 地球物理学报, 41(1): 49-60. Bai C Y. 2004. Three-Dimensional Seismic Kinematic Inversion with Application to Reconstruction of the Velocity Structure of Rabaul Volcano[D]. Australia: The University of Adelaide.
Bai C Y, Greenhalgh S. 2006. 3D local earthquake hypocenter determination with an irregular shortest path method[J]. Bull Seism Soc Amer, 96(6): 2257-2268.
Bai C Y, Greenhalgh S. 2005a. 3-D multi-step travel time tomography: Imaging the local, deep velocity structure of Rabaul volcano, Papua New Guinea[J]. Phys Earth Planet Interi, 151(3-4): 259-275.
Bai C Y, Greenhalgh S. 2005b. 3-D non-linear travel time tomography: Imaging high contrast velocity anomalies[J]. Pure Appl Geophys, 162(11): 2029-2049.
Bai C Y, Greenhalgh S, Zhou B. 2007. 3D ray tracing using a modified shortest path method[J]. Geophysics, 72(4): T27-T36.
Bai C Y, Tang X P, Zhao R. 2009. 2-D/3-D multiply transmitted, converted and reflected arrivals in complex layered media with the modified shortest path method[J]. Geophys J Inter, 179(1): 201-214.
Bai C Y, Huang G J, Zhao R. 2010. 2-D/3-D irregular shortest-path ray tracing for multiple arrivals and its applications[J]. Geophys J Inter, 183(3): 1596-1612.
Bullen K E. 1963. An Introduction to the Theory of Seismology[M]. Cambridge: Cambridge University Press: 189-217.
Inoue H, Fukao Y, Tanabe K, Ogata Y. 1990. Whole mantle P-wave travel time tomography[J]. Phys Earth Planet Interi, 59(4): 294-328.
McNamara D E, Walter W R, Owens T J, Ammon C J. 1997. Upper mantle velocity structure beneath the Tibetan Plateau[J]. J Geophys Res, 102(B1): 493-505.
Scales J A. 1987. Tomographic inversion via the conjugate gradient method[J]. Geophysics, 52(2): 179-185.
Wang C Y, Han W B, Wu J P, Lou H, Chan W W. 2007. Crustal structure beneath the eastern margin of the Tibetan Plateau and its tectonic implications[J]. J Geophys Res, 112(B7): 1-21.
Zhou B, Greenhalgh S, Sinadinovski C. 1992. Iterative algorithm for the damped minimum norm, least-squares and constrained problem in seismic tomography[J]. Exploration Geophysics, 23(3): 497-505.
Zhang H J, Thurber C H. 2003. Double-difference tomography: The method and its application to the Hayward fault, California[J]. Bull Seism Soc Amer, 93(5): 1875-1889.
Zhao W J, Nelson K D, Chen J, Quo J, Lu D, Wu C, Liu X. 1993. Deep seismic reflection evidence for continental underthrusting beneath southern Tibet[J]. Nature, 366(9): 557-559.
下载:
计量
- 文章访问数: 563
- HTML全文浏览量: 259
- PDF下载量: 11
