引言

震动图(ShakeMap)描绘了震后可能的地面运动程度. 它综合利用台站观测值、 震中位置、 震级大小以及震区地质条件等信息， 估计一定区域范围的地震动大小(Wald et al， 1999a， 2006). 其结果能够在地震发生后短时间内以一系列图件的形式发布， 其中尤以直观的震动烈度分布在应急救援和灾害评估中最为常用．

烈度是地震引起的地面震动及其影响的强弱程度． 烈度的大小并不是简单看一个地区房屋的破坏程度， 而是用典型房屋衡量该地区的地面震动情况， 典型房屋在某种程度上相当于地震仪． 烈度分布通常由地震调查组根据调查结果编绘而成， 通常需要几天或几周的时间． 而震动烈度(仪器烈度)一般是根据地震动参数与烈度的经验关系， 在地震发生后快速(几分钟或几小时)计算得到． Wald等(1999b)回归得到了修正麦卡利烈度(Modified Mercalli Intensity)与峰值加速度(PGA)、 峰值速度(PGV)的计算公式， 现被用于美国地质调查局(USGS)的ShakeMap系统． 日本气象厅(JMA)用烈度计的结果进行震后烈度速报. 烈度计是利用加速度记录全振动的等效幅值来计算烈度， 称为“气象厅测定烈度”(Seismological and Volcanological Department， Japan Meteorological Agency， 1996)． 我国的震动烈度主要依据《中国地震动参数区划图》(国家质量技术监督局， 2001)和《中国地震烈度表》(国家质量监督检验检疫总局， 2009)中烈度与峰值加速度的对应关系给出(陈鲲， 2010， 2011a)．

可以看出， 快速生成的震动烈度依赖于地震动参数的快速获取． 对于有台站的场点， 地震动参数可以直接由台站观测数据给出确定性的结果； 而对于无台站的场点， 地震动参数只能由地震动衰减关系给出估计值． 目前我国台站覆盖有限， 且难于实时获取， 快速生成的地震动参数(峰值加速度)主要依赖于经验衰减关系. 再依据烈度与峰值加速度的对应关系， 输出确定性的震动烈度分布．

但是， 衰减关系本身存在着不确定性， 其回归模型中通常都包含一个随机变量ε， 以表征众多未加考虑因素(包括随机因素)所产生的影响(Esteva， 1970； Joyner， Boore， 1981； Brillinger， Preisler， 1985； Abrahamson， Youngs， 1992)． 因此， 将其估计值用于生成确定性的震动烈度分布是不准确的． 而且实践亦证明， 震动烈度与实际调查烈度常常存在较大差异. 基于衰减关系给出的震动烈度分布依赖于衰减模型的选取， 常常是比较规则的形状， 比如圆、 椭圆等; 而实际调查烈度由于断层破裂和能量传播的高度不确定性， 其分布常常是很不规则的．

因此， 本文从衰减关系回归模型中的ε出发， 提出了场点(城镇)遭遇不同烈度的概率计算方法． 具体以1966年3月8日河北邢台M_S6.8地震为例， 利用衰减关系的估计值与衰减关系的标准差， 构造峰值加速度变化的对数正态分布， 以烈度分档对应的峰值加速度范围， 计算震区各城镇遭遇不同烈度的概率以及城镇抗震设防烈度被超越的概率． 作者认为， 与确定性的震动烈度分布相比， 以概率表征的城镇遭遇烈度在表述上更为合理， 建议将其用于震害快速评估．

1.   研究方法

地震发生后， 首先获取的地震参数为震中位置和震级大小， 选择合适的衰减关系可以计算出基岩上任意场点的地震动参数估计值． 地震动衰减关系的一般形式如下：

式中， Y为基岩地震动参数估计值， 如峰值加速度PGA、 加速度反应谱值Sa(T, ξ)， 单位为cm/s²； M为震级， 我国一般采用面波震级； R为距离， 我国多采用震中距， 单位为km； c₁—c₆为回归系数； ε为回归分析中表示不确定性的随机变量．

Esteva(1970)指出， 利用最小二乘方法拟合lnY时(本文取常用对数lgY)， ε服从均值为0、 标准差为σ的正态分布， 这是线性回归的基本假定． 因此可以认为， 基岩上的地震动参数Z服从对数正态分布， 即

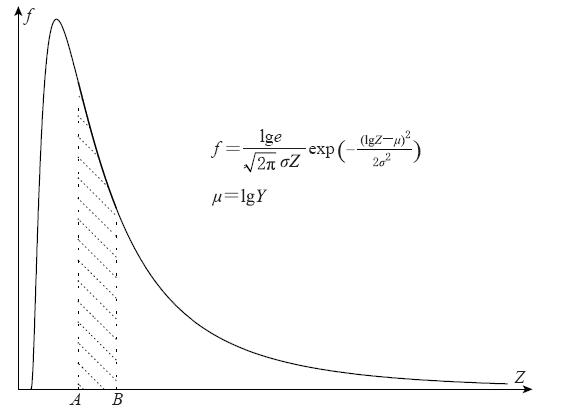
式中， μ为该场点处衰减关系理论计算值Y的常用对数， σ为衰减关系的标准差．Z的分布如图1所示． 图中， f为Z的概率密度函数； A和B为地震动参数积分下限和上限(表1)．

图  1  对数正态分布示意图

Figure  1.  Sketch map of logarithmic normal distribution

下载: 全尺寸图片 幻灯片

表  1  烈度与峰值加速度对照表

Table  1.  PGA intervals for seismic intensity

下载: 导出CSV 

| 显示表格

由概率密度函数的定义可知， Z落在A和B之间的概率为阴影部分的面积． 若地表的地震动参数为Z′， 由基岩地震动参数估计 值Y经过场地校正得到地表地震动参数估计值为犢′,假设Z′仍服从对数正态分布(也中华人民共和国建设部就是说不考虑场地效应的不确定性),则有

当Z′为峰值加速度时,综合考虑《中国地震动参数区划图》(国家质量技术监督局,2001)和《中国地震烈度表》(国家质量监督检验检疫总局,2009)烈度分档情况,Ⅸ 度以下采用《中国地震动参数区划图》中烈度与峰值加速度的对应关系,Ⅸ度及以上采用《中国地震烈度表》的分档原则,对相应峰值加速度区间进行积分,可以得到场点发生对应烈度的概率.烈度与峰值加速度对照关系如表1所示.

2.   实例计算

1966年3月8日5时29分14秒,河北邢台(114.92°E,37.35°N)发生犕S6.8地震,震源深度8km,震中烈度Ⅸ度强(国家地震局地球物理研究所,河北省地震局,1985).控制邢台地震活动的地质构造单元是束鹿凹陷,其东西两侧分别是衡新凸起和隆尧凸起,呈北北东向平行展布.衡新凸起和隆尧凸起的相对上升与束鹿凹陷的相对下沉,造成了该地区地壳强烈的差异运动(河北省地震局,1986),引发了这次地震.本文以此地震为例,对研究方法加以说明.

首先,选用第四代地震动参数区划图所采用的中国西部峰值加速度椭圆衰减关系( 汪素云等,2000)计算基岩上的峰值加速度估计值犢.其中长轴方向采用邢台地区活动断层走向和邢台地震震源机制解(河北省地震局,1986)的结果,取为N27°E.然后,利用基于地形坡度的场地放大系数(Wald,Allen,2007;陈鲲等,2010),将基岩峰值加速度估计值犢转换到地表,得到各城镇的峰值加速度估计值犢′.最后,对每个城镇以峰值加速度估计值犢′和衰减关系的标准差σ(本文取σ=0.242)构造地表峰值加速度Z′的对数正态分布,参照表1对相应峰值加速度区间进行积分,可以得到各城镇遭遇不同烈度的概率.计算结果见表2.

表  2  震区城镇可能遭遇的烈度及其概率

Table  2.  Possible intensity and corresponding probability for counties in seismic area

下载: 导出CSV 

| 显示表格

3.   分析与讨论

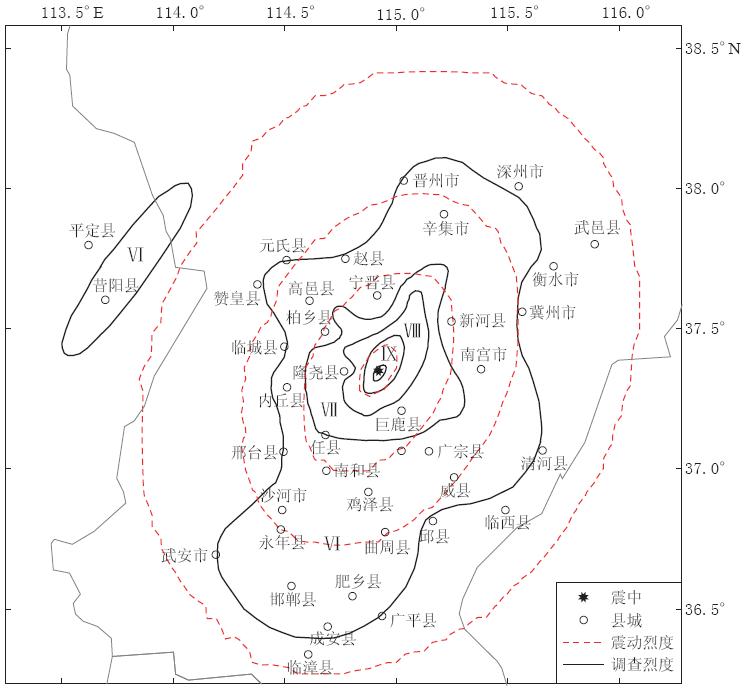
图2给出了邢台地震的震动烈度与调查烈度分布图.其中,实线为实际调查烈度,由邢台地震考察队宏观地震调查组根据1058个调查点编绘而成;虚线为震动烈度,最外圈为Ⅵ度,最内圈为Ⅸ度,由表1最后一列地表PGA 范围给出.例如将PGA 约等于40cm/s2的等值线认定为烈度Ⅵ度等震线,以此类推.可以看出,震动烈度与调查烈度除了Ⅸ度区基本一致外,其它等震线均相差很大,震动烈度的等震线几乎为规则的椭圆,但调查烈度的等震线很不规则.另外震动烈度没有给出昔阳县一带烈度异常的Ⅵ度区.因此,震后仅靠震动烈度分布来估计地震引起的地面震动及其影响将存在较大偏差.

图  2  邢台M_S6.8地震震动烈度与调查烈度分布

Figure  2.  Shaking intensity and survey intensity of Xingtai M_S6.8 earthquake

下载: 全尺寸图片 幻灯片

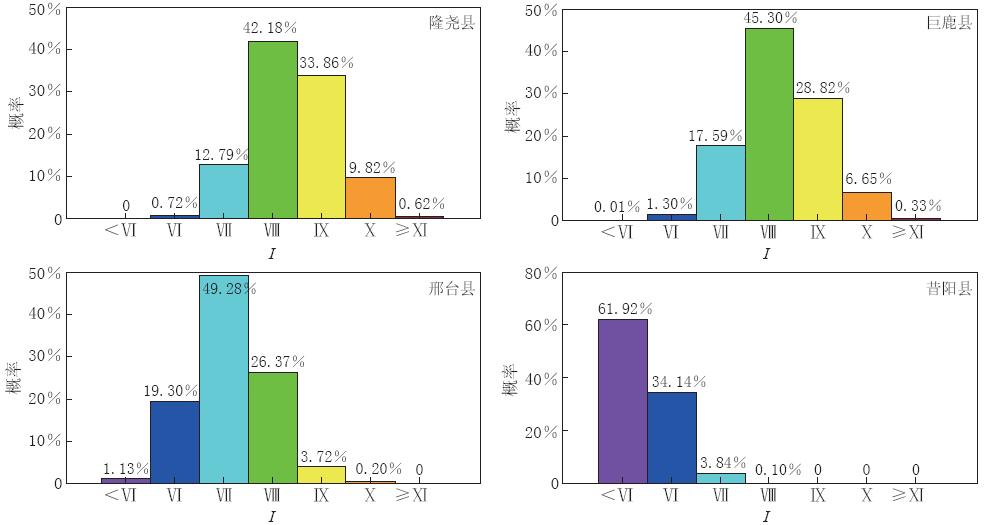
借鉴美国地质调查局(USGS)全球地震响应快速评估系统对死亡人数和灾害损失的概率估计^①,本文建议采用概率方法描述震后城镇可能遭遇的破坏.例如,图3给出了4个城镇遭遇不同烈度的概率分布,能够很直观地估计城镇在地震后最可能遭受何种程度的破坏.对于隆尧县和巨鹿县而言,遭遇Ⅷ度的可能性最高,分别为42.18%和45.30%,但也不能排除遭遇Ⅸ度和Ⅶ度的可能性.实际烈度调查中这两个城镇均遭遇Ⅶ度破坏.对于邢台县,最可能遭遇的烈度为Ⅶ度,但也不能排除发生Ⅷ度和Ⅵ度的可能性,实际烈度调查中邢台县遭遇Ⅵ度破坏.昔阳县距离震中大约110km,最可能遭遇的破坏是Ⅵ度以下,但也不能排除发生Ⅵ度破坏的可能性,而最后实际遭遇Ⅵ度破坏.

图  3  4城镇遭遇不同烈度的概率分布

Figure  3.  Probability distribution of every possible intensity for four counties

下载: 全尺寸图片 幻灯片

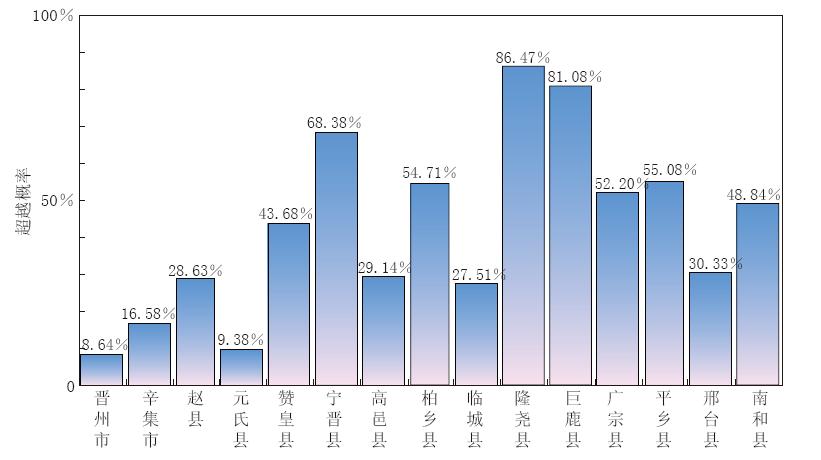
借鉴概率地震危险性分析的思路， 本文计算了地震发生后各城镇抗震设防烈度的超越概率． 其中抗震设防烈度根据《建筑抗震设计规范》(中华人民共和国建设部， 国家质量监督检验检疫总局， 2001)取50年超越概率为10%的地震烈度值， 结果如表3和图4所示． 可以看出， 宁晋县、 新河县、 柏乡县、 隆尧县、 巨鹿县、 任县、 广宗县、 平乡县、 威县等9个城镇抗震设防烈度被超越的概率均在50%以上， 因此, 如果类似地震发生， 应该对这些城镇加大救灾投入.

表  3  震区各城镇抗震设防烈度的超越概率

Table  3.  Probability exceeding seismic fortification intensity for counties in seismic area

下载: 导出CSV 

| 显示表格

图  4  部分城镇抗震设防烈度超越概率柱状图

Figure  4.  Histogram of probability exceeding seismic fortificationintensity for several counties in seismic area

下载: 全尺寸图片 幻灯片

通过以上分析可以看出， 仅靠震动烈度分布来估计震区的地震影响程度将存在较大偏差． 因此本文建议， 在地震发生后能同时给出震区各城镇遭遇不同烈度的概率， 以及各城镇抗震设防烈度被超越的概率， 从中权衡按照几度烈度进行地震备灾， 以实现资源有效配置．

4.   讨论与结论

本文从衰减关系模型中的ε出发， 提出了城镇遭遇不同烈度的概率计算方法． 某地区发生地震后， 利用本文提出的概率计算方法可以快速估计周围城镇可能遭受的烈度， 以及抗震设防烈度被超越的概率， 从而有效指导救灾和资源配置． 另外， 城镇遭遇烈度的不确定性会直接影响随后震害评估的不确定性， 因此建议将本文提出的以概率表征的城镇遭遇烈度用于震害的快速评估， 以此来描述遭遇烈度的不确定性对震害评估结果的影响．

本文仅以峰值加速度计算了城镇遭遇不同烈度的概率， 但是地震发生后， 人们不仅关心人口密集城镇的破坏情况， 还要避免核电厂、 大坝、 超高层建筑、 大型地下管线等重大工程发生次生灾害． 因为这些工程一旦遭到破坏， 可能导致水灾、 火灾、 爆炸、 剧毒或者强腐蚀性物质大量泄露． 例如2011年3月11日日本东北部大地震造成的少量核泄漏至今未绝． 因此， 未来将重点从特定周期加速度反应谱出发， 使用概率方法评估地震对重大工程可能造成的影响．