引言

地震子波提取是地震勘探中一个重要的研究课题， 在反褶积、 反演处理中具有重要作用． Robinson (1957)认为， 地震记录x(t)可以表示为地震子波w(t)与反射系数序列r(t)褶积附加观测噪声v(t)的形式

式中， *表示褶积．式(1)中除了地震记录外， 反射系数序列、 子波和噪声都是未知的， 因此提取地震子波是一个典型的盲估计问题． 为解决这一问题， 在过去的几十年出现了很多种技术， 典型的一种方法是假设反射系数序列是高斯白噪声， 子波相位是最小相位的， 那么子波就可以采用传统的二阶统计量的方式进行提取． 然而子波往往不是最小相位的， 结果这种方法就不再满足实际处理的要求．

为进行混合相位子波提取， 在假设反射系数序列是非高斯、 独立同分布的时间序列前提下， Matsuoka Ulrych (1984)最早将高阶统计量理论用于子波相位谱的提取． 基于高阶统计量理论Tugnait (1987)提出了累积量匹配法， 即在最小平方误差意义下匹配地震记录的四阶累积量与子波矩来进行混合相位子波提取， 并进行了模型验证． 其后， Lazear (1993)将Tugnait的方法应用于实际数据处理中． 累积量匹配法实际上是一个非线性最优化求解问题， Velis Ulrych (1996)等利用快速模拟退火方法对该问题进行求解， 以获得全局最优解， 并对地震记录的四阶累积量加高阶窗来提高估计的稳定性． Liang Gai (2002)结合测井数据， 利用地震记录的三阶或四阶累积量通过外推获取空变的混合相位子波． 戴永寿等(2008)利用自回归滑动平均模型对地震子波进行参数化建模， 并与基于高阶统计量的矩阵方程法相结合， 提出了基于高阶累积量自回归滑动平均(auto-regressive and moving avevage, 简写为ARMA)模型线性非线性结合的地震子波提取方法． 然而， 高阶统计量方法稳定性严重依赖于大量的可用数据(唐斌， 尹成， 2001； Gao， Zhang， 2010)． 地震数据一般都是有限采样， 而且还存在较强的时变性， 因而， 基于高阶累积量的地震子波提取方法在实际应用中还存在一定的局限性．

常规的二阶统计量不包含系统的相位信息，Xu等(1995)对于单输入多输出(single input multiple output， 简写为SIMO)系统的研究指出， 使用二阶循环统计量可以进行非最小相位系统的盲辨识． 本文的矢量预测法就是基于这种思想提出的． 相对于高阶统计量而言， 二阶循环统计量计算速度快， 不需要大量的统计样本数据就能够得到稳定的统计效果(杨绿溪， 2007； Gesbert， Duhamel， 2000； Schmid， Enzner， 2011)． 笔者将动、 静校正处理后的共中心点(common mid-point， 简写为CMP)道集数据视为SIMO系统的输出， 利用CMP地震数据中相邻两道或多道数据通过矢量预测来构建反子波计算的方程式， 进一步进行混合相位子波提取或反褶积处理． 在CMP道集上做反褶积处理， 能够校正子波振幅、 频率、 相位的一致性， 达到同频带、 同向叠加， 提高叠加的质量． 同时利用提取获得的各道相位信息， 对CMP道集进行纯相位滤波也能达到相位校正的目的．

1.   问题描述

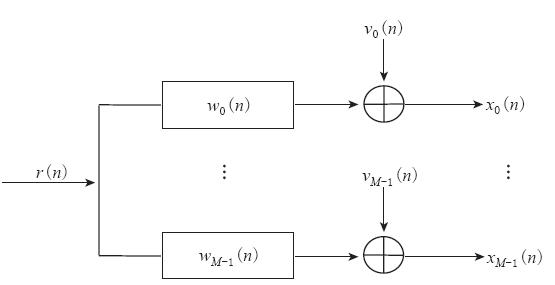
对于CMP道集而言， 假设各道(或相邻两道)的反射系数是相同的， 而各道(或相邻两道)的激发能量、 检波器响应以及检波器与地表耦合效应 等(即地震子波)都是不相同的(下面3.3节对这一假设的适用性进行了验证)． 把反射系数视为单一信号作为系统的输入， 各道的震源子波、 地层滤波、 检波器响应及检波器与地表耦合的滤波效应等作为系统响应函数， 把接收到的地震数据作为该滤波系统的输出， 则这一系统就可以看成是一种SIMO系统． 图1是SIMO系统的示意图. 其中， r(n)为输入信号， w_i(n)为各道的系统响应函数， v_i(n)为观测噪声， x_i(n)为各道的输出．

图  1  单输入多输出(SIMO)系统示意图

Figure  1.  Single input multiple output(SIMO) system

下载: 全尺寸图片 幻灯片

将公式(1)的连续的褶积模型离散化， 即

式中，i表示第i道记录， N是观测时窗的长度， 子波长度为L_w+1．基于SIMO系统理论， 将上述褶积模型矢量化如下：

其中， x (n)=[x₀(n), x₁(n), …, x_M-1(n)]^T([ ]^T表示转置)是n 时刻CMP道集中M道检波器接收到的观测矢量， w(k)=[w₀(k), w₁(k), …, w_M-1(k)]^T是该M道记录所对应的地震子波． 为表述方便， 将式(3)的褶积模型写成矩阵相乘的形式

式中， 下标N表示每道记录观测时窗长度. 其中， X _N(n)和 V _N(n)是NM×1的矩阵； r(n)为(N+L_w)×1的矩阵； W 为NM×(N+L_w) 的分块Toeplitz矩阵， 即

将CMP道集数据视为SIMO系统的输出， 则子波提取及反褶积问题就变成了已知SIMO系统的输出 X _N(n)， 来获取各道子波 w (k)及其反子波的过程．

2.   方法原理

令M道子波w_i(n)对应的反算子为g_i(n)， 并设反算子长度为L_g+1， 则

式中， 上标d表示延迟， d∈[0, L_w+L_g]． 令N=L_g+1， 则式(5)可以写成矩阵相乘的形式

This page contains the following errors:

Below is a rendering of the page up to the first error.

2.1   矢量预测

1) 考虑如下的矢量预测问题. 用过去的L_g个观测矢量 X _Lg(n-1)对n时刻的观测矢量 x (n)进行预测(详见附录A)， 预测误差为

式中， φ (n)是M×1的预测误差矩阵， I _M是M×M的单位矩阵， P 是M×ML_g的预测系数矩阵． 最小化预测误差， 实际上是求解如下优化问题：

This page contains the following errors:

Below is a rendering of the page up to the first error.

假设反射系数序列是零均值、 独立同分布的， 观测噪声为白噪声且与反射系数序列相互独立

估计噪声的方差σ²_v(目前有较为成熟的噪声方差估计方法在此不做赘述)， 消除噪音对信号自相关估计的影响， 可得有效信号的自相关矩阵为

相应的式(8)转变为

记 R _XS的前M列为 R ₁， 后L_gM列为 R ₂， 即 R _XS=[ R ₁ R ₂]. 令 Φ 对预测系数矩阵 P 的偏导数等于零， 可推导出(详见附录B)：

对 R _XS左乘( g ₀)^T 可得

结合式(12)和式(13)可得

计算式(11)优化问题可求出最小预测误差的协方差矩阵Φ、预测系数矩阵 P 及 w (0) (详见附录B)， 从而获得延迟d=0时的反子波 g ₀．

2) 记 W (d, : )和 W ( : , d)分别代表矩阵 W 的第d行元素和第d列元素， W (r₁ : r₂, c₁ : c₂)表示 矩阵 W 中从第r₁行到第r₂行, 从第c₁列到第c₂列元素所对应的子矩阵．观察矩阵 W有

根据这一特性可推导出(详见附录C)

式中， R ^d_XS=E{ X _Lg+1(n) X ^T_Lg+1(n-d)}． 结合式(14)与式(16)有

式中#表示矩阵的伪逆， 至此由多道观测数据的二阶循环统计量计算出了反算子g _d．

2.2   混合相位子波估计及反褶积

上述步骤计算得到反算子 g _d， 可由下式进行反褶积处理：

其中，

X 为观测数据， r为反褶积输出结果．

已知反算子 g _d， 由公式(5)可知， 计算子波的公式为

其中，

3.   模型测试

为了验证本文方法的适用性及处理效果， 选择人工合成的模拟信号及实际地震数据进行混合相位子波提取． 为测试方法的稳定性及数据长度对方法的影响， 数值模拟均进行了100次随机统计实验．

3.1   混合相位子波提取

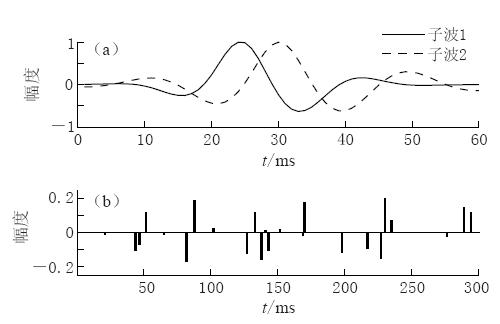
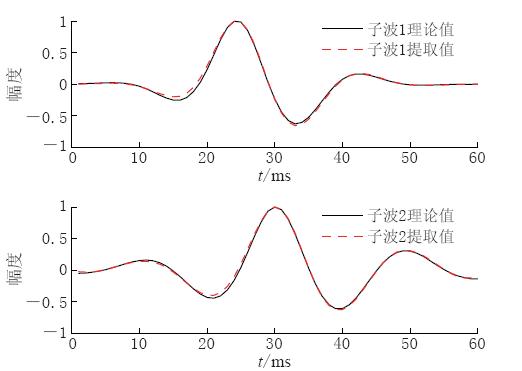
用两个主频为50 Hz的幅度和相位特性各不相同的混合相位子波(图2a、 表1)与随机生成的零均值、 独立同分布(贝努利-高斯分布)的反射系数序列(图2b)， 按式(3)生成SIMO系统的输出序列(图3a， b)， 并由该输出序列构成观测矢量(图3c)， 合成数据为1ms采样.该数据模型满足本文方法的假设前提:① 各道子波之间存在差异;② 各道数据中反射系数序列是相同的,并且满足独立同分布特性.因此,在没有噪声存在的情况下,按照 文中所述方法进行子波提取,理论上讲能够得到较精确的混合相位子波提取值.图4 是实际提取出的子波波形与理论模型(原始子波模型)的对比图. 从图4中的对比可看出， 子波提取值与理论值基本吻合. 这一方面说明了文中所述方法正确， 另一方面也说明了当数据满足该方法适用的假设前提条件时， 利用该方法进行子波提取能够得到满意的子波提取结果．

图  2  子波(a)与反射系数(b)

Figure  2.  Wavelet (a) and reflection coefficient (b)

下载: 全尺寸图片 幻灯片

图  3  合成地震记录及观测矢量构成

Figure  3.  Synthetic records and observation vector which is made up of the synthetic records

下载: 全尺寸图片 幻灯片

图  4  本文方法提取子波的结果与理论模型的对比

Figure  4.  Comparison of the result of wavelet extracted based on this article method and the theoretical model

下载: 全尺寸图片 幻灯片

表  1  图2a中部分时刻的子波值

Table  1.  Value of wavelet in Fig.2a

下载: 导出CSV 

| 显示表格

3.2   数据长度对子波提取的影响

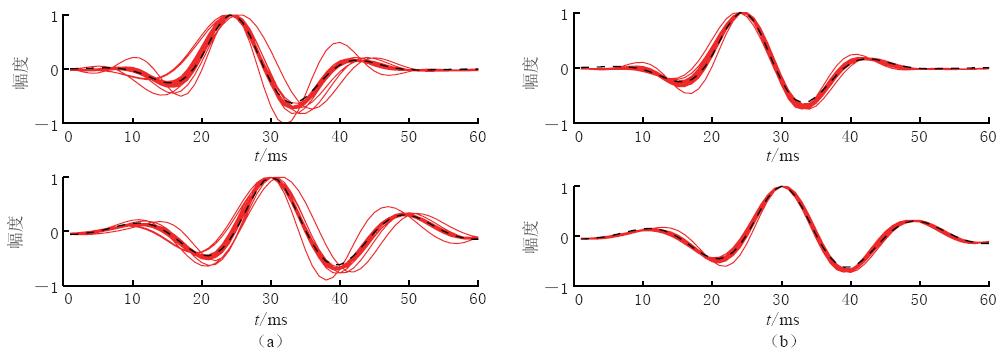
为考察数据长度对本方法的影响， 分别选取记录长度为400， 800 ms， 并采用100次随机实验(保持子波不变， 每次试验随机生成贝努利-高斯分布的反射系数序列并与子波合成地震数据作为观测数据)， 验证不同数据长度对提取子波的影响， 对比结果见图5．

图  5  数据长度400 ms (a)和800 ms (b)时矢量预测法提取子波的100次随机实验结果

Figure  5.  The extracted wavelets based on the vector prediction for data lengthof 400ms (a) and 800ms (b) (100 random tests)

下载: 全尺寸图片 幻灯片

由图5可知， 不同数据长度下， 本文方法均能得到相对稳定的子波提取值. 但提取出的子波与子波理论值或多或少存在一定的偏差， 这是由于模拟的反射系数序列不完全满足白噪特性， 这使得数据不完全满足方法的假设前提造成了估计的偏差． 对比图5a与b可知, 随着数据长度的增加子波提取的稳定性有所改善， 但仍存在一定程度的估计误差． 数据长度越长， 相应的反射系数序列长度越长， 越能满足独立同分布的统计特性. 因此， 数据长度通过反射系数的统计特性来间接影响方法的提取性能. 从图5中可以看出, 数据长度对方法的提取性能影响不大．

3.3   人工合成CMP道集测试

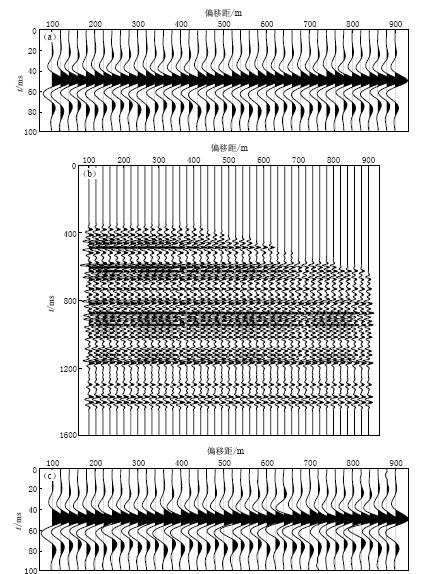
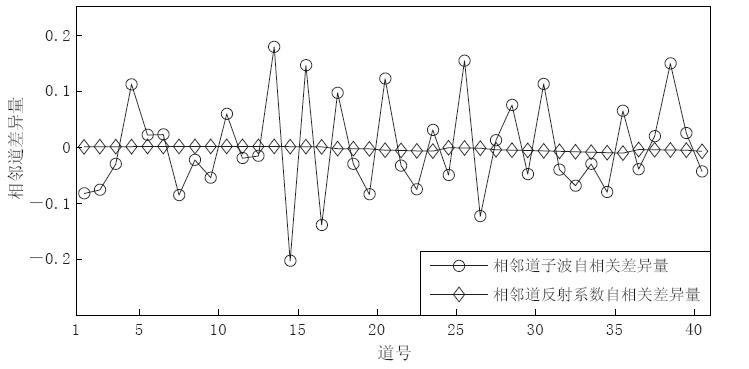
图6a中一系列的频率和相位各不相同的子波来代表实际采集中各道记录对应的子波， 各道的反射系数由Zoeppritz方程(偏移距和入射角的关系由平滑过的P波速度经过射线追踪得到)计算得到. 将各道的子波与反射系数褶积得到合成的CMP道集. 为验证该理论对CMP道集的适用性， 将合成的CMP道集相邻的两道作为SIMO系统的输出(M=2)， 分别计算对比了相邻两道子波与反射系数各自自相关的差异， 见图7．

图  6  对人工合成的CMP道集进行混合相位子波提取(a) 模拟的各道子波; (b) 利用(a)图的各道子波与由Zoeppritz方程计算得到的反射系数褶积得到合成地震记录; (c) 用本文方法由(b)图的CMP道集提取出的混合相位子波

Figure  6.  Mixed-phase wavelet extraction based on the data of synthetic CMP gathers(a) Modeled multi-channel wavelet； (b) Synthetic records obtained by convoluting the wavelets in Fig.6a and the reflection coefficients calculated from the Zoeppritz equation； (c) Extracted mixed-phase wavelets from CMP gathers in Fig.6b by using the method of this paper

下载: 全尺寸图片 幻灯片

图  7  相邻两道子波与反射系数各自自相关的差异量对比

Figure  7.  Comparison between the autocorrelation difference in two adjacent wavelets and that in two adjacent reflection coefficients

下载: 全尺寸图片 幻灯片

从图7的对比可知， 与相邻两道子波自相关的差异量相比， 相邻两道反射系数自相关的差异非常接近于零， 那么对于CMP道集而言公式(9)成立． 所以将CMP道集中相邻两道或多道视为SIMO系统的输出是合理的． 特殊情况下， 当遇到某相邻两道子波相同时， 为便于说明， 假设第10道与第11道记录的子波是相同的， 那么仍可以由第9道与第10道记录构成SIMO系统进行混合相位子波提取， 同时也就得到了第11道记录的子波提取值，因此本文所提方法完全适用于CMP道集．

图6c是利用本文方法从人工合成CMP道集(图6b)提取出的各道混合相位子波. 与图6a对比可知， 子波提取值与理论值相位形态基本一致．

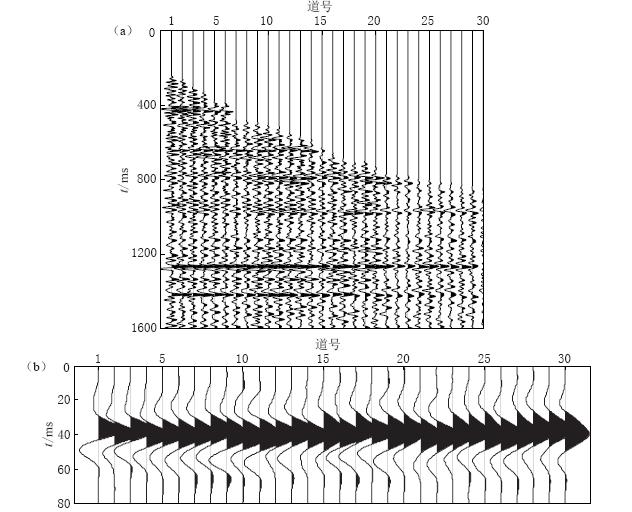
4.   实际资料处理

选取某工区2 ms采样， 动校正后的由30道记录构成的CMP道集(图8a)， 采用本文方法进行混合相位子波提取， 结果如图8b所示. 从子波提取结果可看出, 本文方法适用于CMP道集混合相位子波提取． 需指出， 该方法在混合相位子波提取过程中涉及到矩阵伪逆的计算， 提取出的混合相位子波中会存在一定的高频噪音(该噪音处于地震数据的有效频带外). 采用滤波的方式滤除该噪音， 能够提高子波提取的质量．

图  8  实际资料混合相位子波提取(a) 动校正后的CMP道集; (b) 提取出的混合相位子波

Figure  8.  Real seismic record example: mixed-phase wavelet extraction based on the method of this paper. (a) CMP gather after NMO； (b) Extracted mixed-phase wavelets

下载: 全尺寸图片 幻灯片

5.   讨论与结论

地震子波提取一直是地震勘探中的一个重要研究课题． 本文在地震记录的CMP道集满足SIMO系统的假设基础上， 提出了一种利用二阶循环统计量进行混合相位子波提取的方法． 文中对所述方法进行了模型仿真和实际资料处理， 分析了假设条件对地震记录CMP道集的适用性， 以及影响方法稳定性的因素， 从而得出以下结论与认识：

(1) 与传统的自相关法相比， 利用二阶循环统计量能够进行非最小相位系统辨识． 模型试验验证了当地震记录的CMP道集满足SIMO系统的假设前提下， 可以提取混合相位的子波， 并且精度较高．

(2) 利用二阶循环统计量进行子波提取， 需要假设反射系数序列是独立同分布的． 文中分析阐述了数据长度影响反射系数序列的统计特性， 进而影响到了子波提取的质量． 多次试验的统计分析表明， 数据长度对子波提取质量的影响不大， 并且随着数据长度的增加， 子波提取精度有所提高．

(3) 本文从CMP道集的二阶循环统计量出发， 首先计算各道地震子波的反子波， 再构建方程由反子波来计算子波， 计算比较繁琐． 因此需要进一步简化子波提取的目标函数， 由已知的CMP道集的二阶循环统计量直接计算子波， 简化计算步骤， 目前该工作正在进行中．

(4) 在计算反子波与子波的过程中都涉及到矩阵伪逆的计算， 在该方法的数据求逆中, 高频噪音的影响会被放大， 当地震数据信噪比较低时解的高频端可信度较低． 由于地震仪器接收到的信号一般都是带限的信号， 在地震数据有效频带范围外有效信号几乎接近于零， 所以在有效频带外子波一般可以做置零处理． 因而对低信噪比数据提取出的混合相位子波做适当的滤波处理能够提高解的质量．

附录 A

记：

用过去的L_g个观测矢量L_g(n-1)对n时刻的观测矢量(n)进行预测， 令预测算子为， 则预测误差为

式中， 如[I_M 0_M×MLg]表示M×M（L_g+1）的矩阵，该矩阵的前M列是M×M的单位矩阵， 后MLg列是M×M_Lg的全零矩阵．

附录 B

求解如下的最优化问题

This page contains the following errors:

Below is a rendering of the page up to the first error.

将式(B2)对P求导：

令导数为零， 可得

This page contains the following errors:

Below is a rendering of the page up to the first error.

至此， 可由有效信号的自相关矩阵?R_XS计算得到预测误差协方差矩阵Φ和预测系数矩阵P?分别为

若记?R_XS的前M列为R₁， 后L_gM列为R₂， 即R_XS=［R₁ R₂］， 由式(B5)可得

假设反射系数序列是零均值、 独立同分布、 方差为?σ²_r的时间序列， 则

This page contains the following errors:

Below is a rendering of the page up to the first error.

由式(B6)可得

This page contains the following errors:

Below is a rendering of the page up to the first error.

由上式可见， 预测误差的协方差矩阵?Φ的每一列都正比于w(0)， 由上式可以计算出w(0)．至此，由SIMO系统输出的自相关R_XS通过式(B6)、 式(B12)计算出最小预测误差的协方差矩阵Φ、 预测系数矩阵P、 及w(0)．

附录 C

考察矩阵W有如下关系：

所以

则

This page contains the following errors:

Below is a rendering of the page up to the first error.

由于，

所以，