引言

核查地震波形数据记录中确定时间系统的精度是数字地震台网最困难的任务之一，特别是当波形数据进行离线保存或使用时，其时间系统的精度则更加具有不确定性(Schnfelder，2008)． 尽管目前数字地震台网中都普遍采用了GPS来进行授时，但当GPS重复不断地连接外部时钟失败时，数据的记录时间就只能依赖于内部时钟(Bormann，2012)． 通常情况下，内部时钟的校正信息会以日志的形式进行保存，但在没有GPS信号期间的精确时间则是无法估计的； 或日志信息不随数据一起分发，那么对于数据的使用者来说，依然无法控制时间系统的精确度． 在目前的实时记录系统中，难以及时检测到单台记录的时间误差． 以江苏省数字地震台网目前运行的41个数字地震台为例，2010—2011年期间，在M_L>2.5的188次地震编目过程中，平均每次地震约有1.8个台站因存在大于2 s的钟差而被迫放弃使用其震相．

近年来的大量研究表明，台站对间较长时间的背景噪声互相关函数，在一定程度上可以代表两个地震台站之间真实的格林函数(Campillo，Paul，2003； Shapiro，Campillo，2004； Larose et al，2006； Nakahara，2006； Stehly et al，2006)． 由于较长时间的背景噪声互相关函数可以使随机场中的噪声源和地壳内地震波散射的非均匀性得到足够的平均，从而保证了格林函数的有效性(Sabra et al，2005； Stehly et al，2007)． 利用背景噪声格林函数得到的瑞雷面波信号周期较短(小于20 s)，因此可以获得更高分辨率的区域地壳层析成像结果(Shapiro et al，2005)； 加之背景噪声记录的连续性，这就使得利用背景噪声干涉测量技术监测区域性的、 震源区及火山的地壳结构变化成为可能(Schnfelder，Wegler，2006； Yao et al，2006； Wegler，Schnfelder，2007； Brenguier et al，2008； 刘志坤，黄金莉，2010)． 然而，要真正获得由介质变化引起的相关波速变化信息，依然是困难重重(王伟涛等，2011)． 首先，介质变化引起的相对波速变化十分微小； 其次，格林函数会受噪声源分布变化的影响； 最后，记录数据中长期存在的时间偏差会影响到走时的测量精度，尤其是在自相关格林函数的分析中． 因此可以看出，单台时间偏差，无论对于地震定位、 预警，还是背景噪声层析成像等研究来说，都尤为关键； 如何计算单台的时间误差便成为地震监测技术领域中十分重要的研究内容． Stehly等(2007)运用周期为5—10 s和10—20 s的背景噪声互相关格林函数评估了南加州地震网中3个台站对的时间误差； Schnfelder(2008)则利用基于台站对相对走时差的超定方程，成功地计算出Merapi火山台阵中4个单台的时间偏差．

本文将详细研究基于背景噪声互相关格林函数的单台时间误差的计算方法，并从江苏省数字地震台网中选取两组平均台间距不同的台站(每组4个)对比分析. 这对于提高数字地震台网记录数据的精度和使用效率是有现实意义的．

1.   基本原理

1.1   台站对互相关相对走时的计算

理想情况下，假设在噪声源均匀分布的各向同性介质中，台站对a，b的互相关因果信号走时应在正时间区域内，反方向上的非因果信号走时应在负时间区域内． 对于一个特定的路径和周期范围，由互相关格林函数得到的面波走时是不随时间变化的(Lobkis，Weaver，2001； S′anchez，Campillo，2006)． 然而，理论和实践表明，有以下3种主要因素会导致走时出现扰动(Stehly et al，2007)：

1)介质的物理性质发生改变，会导致互相关走时在正、 负时间区域内出现较快或较慢的现象.

2)台站对中其中一个存在时间误差，或传感器的相位响应发生改变，均会导致互相关函数相对于零线整体发生偏移，即走时在正时间区域内偏大，在负时间区域内偏小. 反之亦然.

3)介质中噪声源的空间分布发生变化，会独立影响正、 负时间区域内的互相关走时. 因为正、 负时间区域内的走时对不同区域的噪声源分布十分敏感．

于是，在某一给定的路径和频带范围内，背景噪声互相关函数中求取的面波走时δτ与“参考走时”之间的偏差，可用下式来表示：

式中，D(t)是由台站时钟误差(或传感器的相位响应偏移)引起的时间延迟，它是偶函数(Stehly et al，2007)； φ(t)是由于介质物理性质改变引起的走时扰动，Sabra等(2005)在研究海洋声学时指出其性质属于奇函数； ε(t)是由于噪声源在空间上的分布变化而引起的时间偏移，它可以通过增加互相关函数的时间序列长度使噪声源的分布均匀化，从而最大限度地减小其对走时的扰动．

取式(1)的奇、 偶部分变形后可得

当D(t)和φ(t)远大于[ε_ij(t)±ε_ij(-t) ]/2时，通过滑动窗互相关技术(Clarke et al，2011)测量求出δτ_ij(t)后，利用式(2)、 式(3)即可求出D(t)和φ(t)． 但需要指出的是，在测量过程中使用小尺度的时间窗(如1个月)虽然可以得到分辨率较高的时间偏差，但小时间窗会使得ε(t)偏大，因此只能测量出由明显时钟误差引起的走时差； 使用大时间窗则会降低分辨率，但会使ε(t)减小，从而可以更容易识别出小的时钟误差和介质物理性质的变化(Stehly et al，2007)．

1.2   单台时钟偏差的计算

D(t)是台站对间格林函数的相对时间偏差，而不是单台的绝对时间偏差． 虽然在背景噪声的层析成像中十分有用，但它无法应用于提高地震事件的定位精度及利用背景噪声干涉技术对地壳结构变化进行长期监测，因为它们都高度依赖于单台记录的时间精度． 为了能够计算出单台的绝对偏差，Schnfelder(2008)提出了将台站对间格林函数的相对走时误差ΔD_Si-Sj与单个台站的时间偏差ΔS_i之间的关系，可用下面的矩阵表示：

则当式中系数矩阵中非零值对应的ΔD_Si-Sj已知时方程是有效的，即转换为线性方程的求解

式中，d是已测量出的台站对间格林函数相对于“参考格林函数”的走时误差； m是未知向量(至少大于4个)，即待求的单台时间误差． 由于G是i×j维的矩阵，且i>j，于是方程的求解就变成了典型的超定方程反演

G^-g为G的广义逆矩阵，可以通过奇异值分解最小二乘法来求得近似解，即当m使‖Gm-d‖₂达到最小时的解(张志涌等，2011)． 然而ΔD与地球介质、 单台时间误差、 噪声源分布及记录仪器的系统误差等均有关系，它的产生是非线性的． 式(5)实质是根据泰勒级数展开将非线性化方程组线性化的过程，因此，对计算结果的可靠性和误差进行分析也就十分有必要． 为了获得不同置信水平下的结果和误差范围，本文引入协方差矩阵来进行估计. 假设当观测数据的随机误差满足正态分布时，未知向量m的计算误差总和可以用协方差矩阵来表示(Menke，1984)

式中，C_d为数据的协方差，σ为与测量数据相关的标准差．

2.   数据处理及实验

2.1   噪声源分析

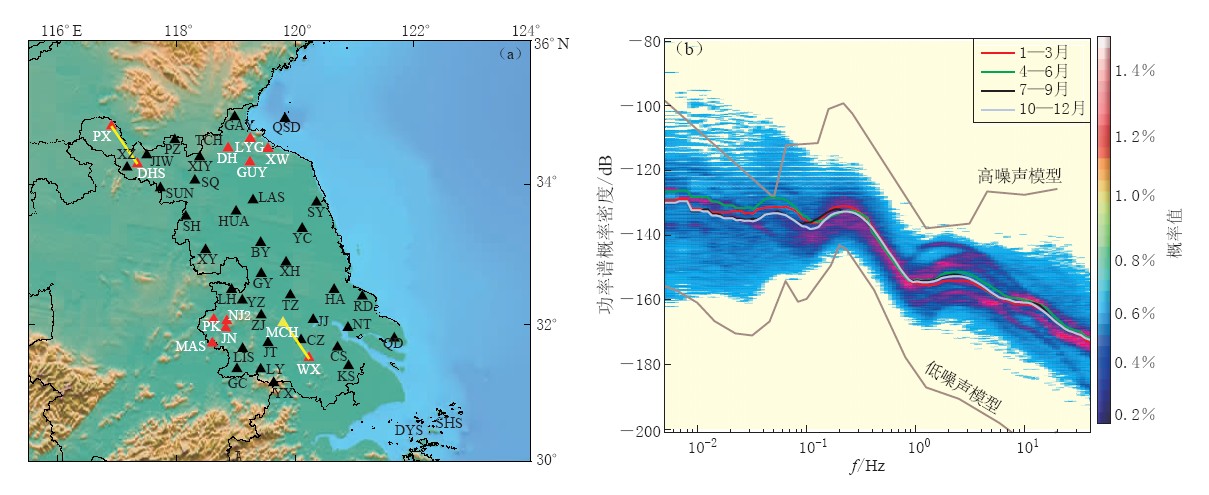
Stehly等(2006)研究表明，0.1—0.2 Hz频带范围内的噪声源能量稳定，且不随季节发生变化. 由它求取的格林函数形态稳定，重复性高． 为了解江苏省区域噪声源的具体特征，本文首先采用功率谱概率密度函数方法(McNamara，Boaz，2005； 王俊等，2009)，对2011年江苏省41个宽频带数字地震台的背景噪声水平进行计算分析. 其中28个地震台是地面台，频带范围为60 s—50 Hz； 13个地震台是井下台，频带范围为120 s—50 Hz. 采样率均为100 Hz． 江苏省位于我国的东部沿海，41个台站距海岸线的平均距离约为167 km，平均台间距约为45 km(图 1a)． 以各台站每小时垂直向的连续记录为样本(共计11972条)，计算所有功率密度谱随频率的概率分布，取概率最大处的值来代表江苏省区域的背景噪声水平值(图 1b)． 按季节统计的结果显示： 0.1—0.5 Hz和0.03—0.1 Hz范围内的噪声能量基本相当，但其中0.1—0.5 Hz范围内的噪声源更加稳定，0.03—0.1 Hz范围内的噪声则会随季节变化出现5 dB左右的扰动，因此本文用来求取背景噪声互相关格林函数的频带范围扩大为0.1—0.5 Hz．

图  1  选用的台站分布示意图(a)和2011年江苏省台站背景噪声的功率谱概率密度(b)

Figure  1.  The distribution of seismic stations in this study (a) and the probability density function of power spectrum density of ambient noise in Jiangsu Province in 2011(b)

下载: 全尺寸图片 幻灯片

2.2   数据预处理

为保证格林函数计算的连续性和完整性，要求所选台站2011年的垂直向连续记录数据、 年运行率和每天的波形完整率均大于99.0%． 在进行互相关格林函数计算前，需对单台每一天的数据进行必要的处理：

1)扣除仪器响应和线性趋势.

2)将每一天的连续波形数据按00：00：00—24：00：00进行相对同步和截断.

3)利用Butterworth滤波器进行0.1—0.5 Hz的带通滤波.

4)采用在时域内的滑动窗绝对均值归一化法(the running-absolute-mean normalization)对波形数据进行归一化，归一化的权重因子定义如下式:

This page contains the following errors:

Below is a rendering of the page up to the first error.

5)在0.01—1 Hz频带范围内进行频谱白化后，再返回到时域得到单台背景噪声数据．

2.3   实验性计算

挑选了路径方向和台间距都相近的台站对PX-DHS(70.7 km)和MCH-WX(69.3 km)进行试验性计算，台站分布如图 1a中绿色连线所示，以了解单台时间偏差对互相关格林函数走时的影响． 其中已知2011-02-22—2011-04-30的记录数据中，MCH台(图 1a中黄色三角形所示)由于GPS授时故障而存在约+120 s的钟差． 随机计算了此期间内一天的互相关格林函数，结果如图 2a所示. 两组面波的最大振幅均十分清晰，都在正时间区域内； 但MCH-WX相对于PX-DHS，其面波最大振幅整体向正时间区域内偏移了约118.73 s． 图 2b是在XW台原始数据中人为加入±30 s时间误差后，LYG-XW(31.8 km)台站对得到的格林函数，面波信号的信噪比(SNR)和各相位上的连续性同样十分清晰. 相对于由原始数据得到的格林函数，面波走时分别相差±30 s． 这直观地说明了单台的时间偏差，可以真实地、 清晰地反映在台站对互相关格林函数的面波走时上，特别是当时间误差远大于由介质变化引起的走时扰动时．

图  2  2011-03-10台站对PX-DHS和MCH-WX的背景噪声互相关格林函数(a)和2011-01-10 XW台人为加入30 s钟差前(上图)后(下图)的背景噪声互相关格林函数(b)

Figure  2.  The cross-correlation Green’s function of the ambient noise for station pairs PX-DHS and MCH-WX on March 10, 2011 (a) and that for station pair LYG-XW before (upper) and after (lower) artificially adding the 30 s clock error on original data of the station XW on January 10, 2011 (b)

下载: 全尺寸图片 幻灯片

3.   计算结果

3.1   台站对间格林函数的相对走时

为检验不同台间距间和不同环境背景噪声区域下的测量精度差异，选取江苏省数字地震台网中的两组台站来进行对比研究，即A组(DH、 GUY、 XW、 LYG)、 B组(MAS、 JN、 NJ2、 PK)． 各组中台站两两组对来构成台站对，两组中的台站对平均台间距分别为44.6 km和30.5 km，如图 1a中红色三角形所示. 其中B组较A组离海岸边更远． 根据中华人民共和国国家质量监督检验检疫总局(2004)颁布的《地震台站观测环境技术要求》，B组台站在背景噪声区域划分上属于C类地区，A组属于D类地区．

稳定的格林函数是测量走时误差的先决条件，因此有必要对本研究中12个台站对间互相关格林函数的信噪比进行分析，信噪比SNR定义如下式(Clarke et al，2011)

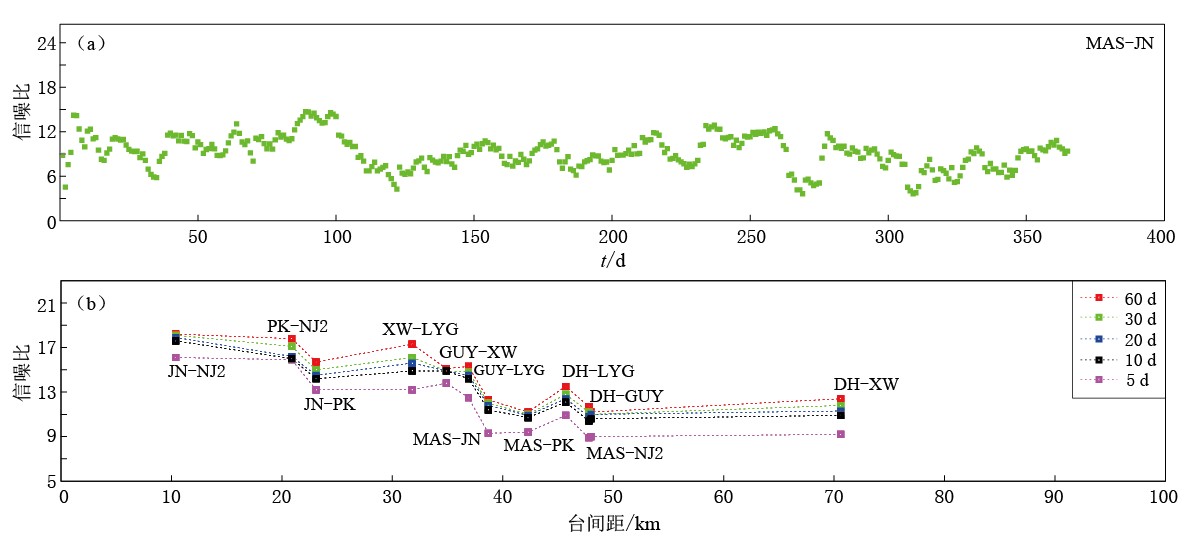
即信号的均方根平方与噪声的均方根平方之比的对数值． 图 3a是台站对MAS-JN(47.8 km)的计算结果. 可以看出，每一天的结果之间存在一定程度上的差异； 所有台站对的信噪比整体上呈现出随台间距增大而减小的趋势(图 3b)． 因此为了保证信噪比，台站对间的距离要尽可能小，这也是选取台站对时需要考虑的一个重要指标． 本文选取的最大台站对距离约为70.6 km，尽管各台站对间格林函数的年平均信噪比均在8以上，但为了保证相对走时的测量精度，将每一天的格林函数沿时间轴进行滑动窗叠加来代表该天的格林函数，以提高信噪比． 图 3b是采用不同窗长(分别为10，20，30，60天)叠加得到的信噪比结果. 可以看出，窗的长度越长信噪比就越高，但提高的相对比例则随着窗长的增加而逐渐趋于平稳． 窗长为10天时信噪比提高比例最大，平均信噪比达到了13.2; 窗长为60天时平均信噪比约为14.3． 于是最后采用的窗长为10天，因为信噪比的提高是以弱化单条格林函数差异为代价的，窗长越长牺牲的个体差异就越明显．

图  3  2011年台站对MAS-JN背景噪声互相关格林函数的信噪比(a)和各台站对 采用不同窗长(分别为10， 20， 30， 60天)叠加得到的信噪比结果(b)

Figure  3.  The signal-to-noise ratio of the cross-correlation Green’s function of ambient noise for station pair MAS-JN in 2011 (a) and the superimposed signal-to-noise ratio results of all station pairs with different window length (10， 20， 30， 60 days) (b)

下载: 全尺寸图片 幻灯片

要测量出台站对间格林函数走时随时间的变化，还须确定出每个台站对的“参考格林函数”． “参考格林函数”通常由长时间尺度(至少1年以上)的格林函数叠加而得，这是为了最大限度地减小随机噪声源变化产生的影响(Schnfelder，Wegler，2006； Stehly et al，2007； Schnfelder，2008)． 本文采用各台站对间2011年的格林函数来叠加，得到各自的初始“参考格林函数”，相对走时的测量步骤具体如下:

1)在流逝时间--200—200 s范围内，沿时间轴滑动地测量每条格林函数与其对应的“参考格林函数”之间的走时差，即通过测量两组波形之间互相关系数最大时的延时差． 因为该时间范围内格林函数的最大振幅，主要反映的是直达波的特征，反射界面对波形的影响较小．

2)联合所有台站对相对于初始“参考格林函数”的走时差均方根，校正各自的初始“参考格林函数”，以消除系统的时间差，进而得到新的“参考格林函数”．

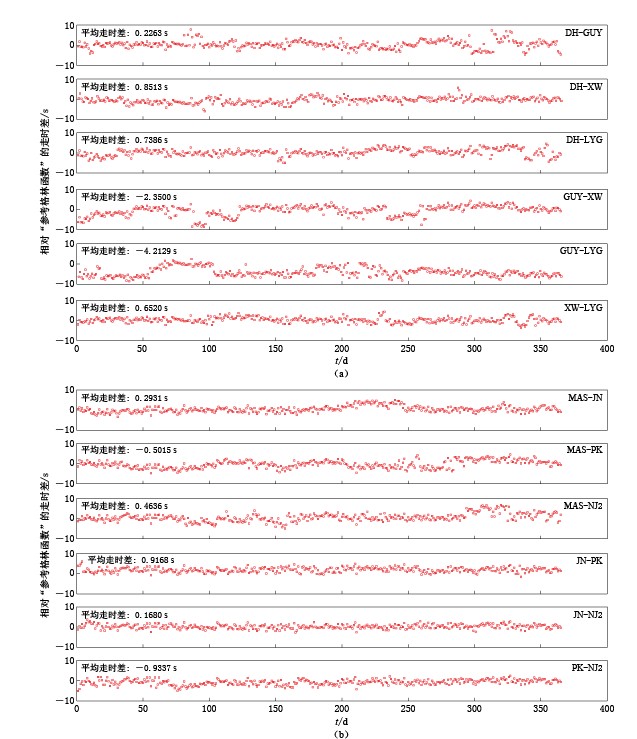
3)重复第一步中的做法，重新测量各台站对相对于新“参考格林函数”的走时差，即ΔD_ij(t)，计算结果如图 4所示．

图  4  2011年A组(a)、 B组(b)台站对互相关格林函数随时间的走时差

Figure  4.  The travel time lag of cross-correlation Green’s function with time for the station pairs of groups A (a) and B (b), respectively, in 2011

下载: 全尺寸图片 幻灯片

从图 4的结果看，A，B两组台站对间格林函数的相对走时差整体均较为稳定，但每一天之间并不完全一致，是起伏变化的． 其中A组中有6个台站对的年平均走时差均方根较大，约为2.042 s. 相比而言，B组的走时差均方根值要小得多，仅为0.865 s，各台站对间的走时误差也未超过±1.000 s． 此外，还注意到A组中的台站对GUY-LYG与GUY-XW的走时差明显偏大，分别为-4.213 s和-2.350 s，而XW-LYG的走时差则为0.652 s. 不难发现，其中2对走时差中存在较大走时差的台站对均有GUY台． 分析认为，它们间的主要走时差可能是由于GUY台的记录数据中存在明显时间误差引起的. 因为在同一区域内噪声源分布和介质结构的变化，不可能只影响某一路径上格林函数的走时变化(Stehly et al，2007)．

3.2   单台的时间偏差

本文不仅旨在计算出单台的时间偏差，同时也对计算结果的置信水平和计算误差给出合理评价． 由1.2节可知，可以运用奇异值分解最小二乘法对式(5)中的系数矩阵G进行分解： [U，S，V]=svd(G)，返回矩阵U，S，V，满足G=USV^T，式(7)的协方差矩阵即可改写为下式(Klein，2002):

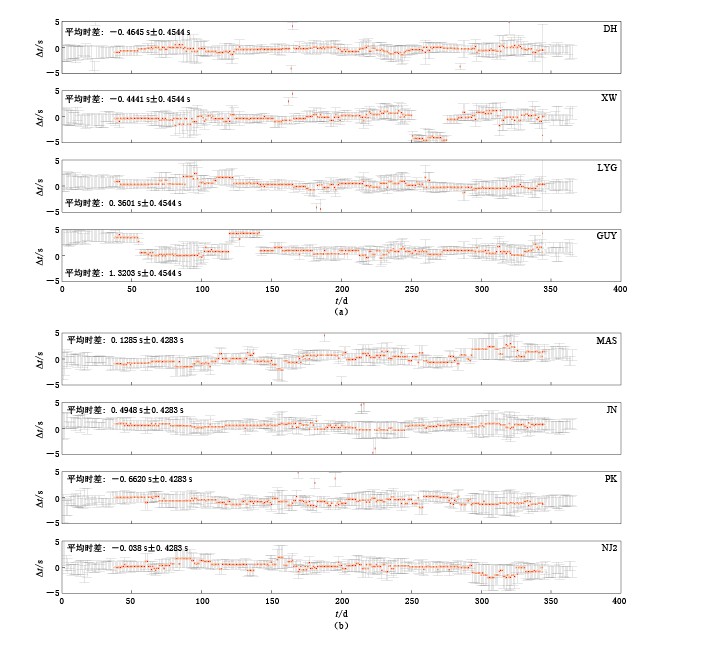
式中，w²=RDEER²+ERCOF×RMS²，是与测量数据有关的标准差平方． RDEER表示含义模型之外的误差，是根据先验误差水平设定的，本文则是根据Hyposat地震定位程序(Schweitzer，2001)，对2010—2011年江苏地区约350次地震定位所给出的平均走时残差而确定的，约为0.386 s； ERCOF表示误差计算的权重因子； RMS为走时残差均方根，即各台站对间每一天的格林函数走时差与年平均走时差之间的均方根． 随后可计算得到协方差矩阵，它是一个4×4维的对称矩阵. 其中与对角元素相对应的本征值，即为各个单台时间偏差的标准误差平方Δσ²． Δσ²·F即为误差范围，F为误差标度因子，它是由置信水平和变量个数共同决定的． Dennis(2008)在地震定位误差的研究中，给出了不同变量个数和不同置信水平下的标度因子值，由于本文只关心各台记录数据中的时间偏差，于是参照其中单变量标度因子的取值(表 1)，分别计算了置信水平为90%、 95%和99%时的单台时间偏差和误差范围，结果见表 1．

表  1  不同置信水平下计算结果的均方根和误差范围

Table  1.  The RMS results and error ranges of calculation results under different confidence level

系数矩阵 G 中的随机误差	置信水平	标度因子	均方根时差/s		误差范围/s
			A组	B组	A组	B组
0.00	90.00%	1.644 9	0.750 1	0.450 4	±0.381 3	±0.359 4
	95.00%	1.960 0	0.750 1	0.450 2	±0.454 4	±0.428 3
	99.00%	2.575 8	0.750 1	0.450 4	±0.597 1	±0.562 8
0.10	90.00%	1.644 9	0.710 5	0.474 6	±0.374 2	±0.367 5
	95.00%	1.960 0	0.783 0	0.473 7	±0.492 6	±0.420 2
	99.00%	2.575 8	0.760 3	0.430 5	±0.618 0	±0.610 2
0.15	90.00%	1.644 9	0.842 0	0.474 0	±0.394 6	±0.378 6
	95.00%	1.960 0	0.762 9	0.446 9	±0.412 3	±0.443 1
	99.00%	2.575 8	0.721 0	0.428 2	±0.531 5	±0.510 7
0.20	90.00%	1.644 9	0.666 6	0.469 6	±0.339 8	±0.307 4
	95.00%	1.960 0	0.672 6	0.434 1	±0.388 8	±0.381 6
	99.00%	2.575 8	0.802 3	0.424 2	±0.624 6	±0.481 7
0.25	90.00%	1.644 9	0.857 8	0.506 3	±0.526 5	±0.509 5
	95.00%	1.960 0	0.786 2	0.565 6	±0.509 3	±0.689 9
	99.00%	2.575 8	0.708 3	0.501 6	±0.527 7	±0.665 1
0.30	90.00%	1.644 9	0.786 9	0.383 7	±0.345 6	±0.376 5
	95.00%	1.960 0	0.837 4	0.495 2	±0.573 3	±0.588 2
	99.00%	2.575 8	0.732 2	0.521 4	±0.558 5	±0.688 2

下载: 导出CSV 

| 显示表格

图 5是置信水平为95%时的计算结果和误差范围. 由该图可以清晰地看到2011年A，B两组中各台站时间偏差随时间的变化情况. 90%的变化幅度在±0.500 s以内，均方根值分别为0.7501 s和0.4502 s，置信水平为95%的误差范围分别为±0.4544 s和±0.4283 s. 这一水平与网内地震定位中走时残差均方根值的量级基本相当． 其中A组的均方根约大于B组，这可能是由于A组中的台间距大于B组，导致格林函数的信噪比减小而引起的测量误差． 更值得注意的是，A组中的GUY台在1—52天、 120—144天期间约有＋3.134 s的明显偏差，意味着GUY台在此期间的时间大于参考时间约3.134 s． 为了检验计算结果是否符合实际情况，采用HYPOSAT定位程序对此期间江苏地区的123条地震进行了定位.结果显示，GUY台的平均走时残差为+2.892 s，即观测到时大于理论到时2.892 s． 考虑到合理误差范围，两者的计算结果几乎一致． 此外，XW台在250—273天期间也存在明显偏差，约为-4.120 s. 同样对在此期间的12条地震进行了定位，显示XW台的平均走时残差约为-4.423 s． 其余6个台站的全年时差均方根为0.4215 s，而利用定位结果得到的平均残差为0.374 s． 这意味着，从背景噪声中直接计算出的单台时间偏差结果是可靠的，与地震定位结果中走时残差的精度也基本接近，有效精度为0.2 s左右．

图  5  2011年A组(a)与B组(b)各台站置信水平为95%时的时间偏差和误差范围

Figure  5.  The time deviation and time error of all stations for groups A (a) and B (b) under 95% confidence level in 2011

下载: 全尺寸图片 幻灯片

此外，为了检验计算结果的稳定性，在A，B两组台站的系数矩阵G中，分别加入均方根值为0.10，0.15，0.20，0.25和0.30的随机误差进行计算，结果见表 1． 通过比较发现，两组台站的时差均方根值均很稳定，最大变化约为0.1819 s，但A组的时差均方根值始终大于B组； 相同置信水平下的误差范围变化也不明显，最大约为0.1775 s． 这表明随机误差对计算结果的稳定性影响很小，计算结果主要还是依赖于台站对格林函数相对走时的测量结果； 而计算精度则与信噪比密切相关．

4.   讨论与结论

4.1   讨论

图 5表明，除由于明显钟差引起的时间偏差外，还能观察到各台全年的结果仍然有较小幅度的波动变化，A，B两组台站的计算误差水平也有相似的扰动，推测这可能与噪声源为全球分布有关． 江苏地区的噪声源实际上是受太平洋和印度洋两大洋的活动影响，其中在150—300天之间扰动变化的一致性更加明显一些. 这可能反映出江苏地区夏季噪声源能量的优势方向来自于太平洋，因为夏季太平洋上台风活动密集会引起噪声源的变化． 2011年5—10月共有20次中心风力大于10级的台风http://typhoon.weather.com.cn/，这使得台站对间互相关格林函数走时出现扰动. 冬季的噪声能量优势方向则可能来自于印度洋的活动． 这方面的研究国内也有学者在开展，如夏英杰等(2011)采用单台研究法对汶川M_S8.0地震前地脉动进行研究时，发现0.2 Hz左右地脉动能量的增加，是由2008年威尔逊台风活动引起的．

0.1—0.2 Hz的噪声源是由于传向近海海岸的海洋潮汐波沿反方向传播叠加而产生的重力波所引起的(Longuet，1950)； 台风产生的海浪与背景海浪场相互作用也可以产生这类信号(张雁滨等，2010)． 从图 1b中的计算结果可以看到，虽然0.1—0.5 Hz的噪声源能量随频率的变化相对于0.03—0.1 Hz的噪声更加稳定，但依然会随季节出现变化，这无疑会对测量精度造成一定的影响． 由0.1—0.2 Hz背景噪声提取的格林函数，对介质的敏感深度约为6 km(Stehly et al，2007)； Schnfelder和Wegler(2006)利用2—8 s频带范围的背景噪声对印度尼西亚Merapi火山地区波速变化进行研究时，认为介质波速随季节性的变化小于1%． 参考前人的研究成果，若以江苏地区P波在地壳浅层中的平均波速为5.1 km/s，台站对间的距离为50 km为例，按1%的速度变化来计算，随季节变化引起的最大走时差约为±2.55 s． 而在本文的实际计算中，采用联合所有台站对相对于初始“参考格林函数”的走时差均方根校正各自对应的初始“参考格林函数”，以最大限度地消除季节性变化对计算结果的影响． 从图 5的计算结果看，除明显时钟误差外，其余结果均未超过±0.500 s． 这一结果表明，尽管包括季节性噪声源随频率的变化以及其它未知因素等对结果的影响并未完全消除，但此计算精度仍可以满足目前地震监测中对单台明显时钟偏差的检测要求． 特别是通过在系数矩阵G中加入不同的随机误差进行计算稳定性的检验，则从另一角度说明了测量方法的可靠性．

此外，在测量相对走时变化的过程中，格林函数的信噪比是影响波形之间相关系数的重要因素． 从图 3中可以看到，格林函数的信噪比会随着台间距的增大而减小，采用10天尺度长的滑动窗叠加代表一天的格林函数，使得在提高波形之间相关系数的同时，却在一定程度上牺牲了每一条格林函数之间的个体差异，以至于计算结果在反映每一天的真实时间偏差时存在一定的失真，但这并不影响测量结果中趋势性变化的真实性． 本文中的台站对平均台间距约为35 km，平均时差均方根为0.4215 s． 而Schnfelder(2008)指出，当台站对间距小于5 km时，从背景噪声中计算出来的单台时间偏差精度可以达到50 ms； 台站对间距小于200 m时能达到10 ms. 两者在量级上基本相符． 在此需要指出的是，在不同相关系数下的测量精度的差异性研究本文没有涉及，这是值得进一步研究的内容．

验证计算结果可靠性最直接、 有效的手段，是利用记录仪器中内部时钟GPS的校正信息，但可惜这些信息目前并没有随波形一起保存在记录数据中，只在实时记录过程中保存在数据采集器的循环缓存中，随着时间的推移保存的信息被不断地刷新，因而无法应用于本研究中． 于是采用地震定位程序中的走时残差来进行验证，这种方式只能验证有地震记录信号期间的时间精度，其精度也低于GPS，因此在效能上存在一定的局限性. 但考虑到地震在时间上的随机性，运用地震定位的走时残差对计算结果进行检验仍然是可信的. 该方法也是目前地震台网检查波形记录中时钟误差的手段之一． 通过比较可以看到，本文从背景噪声中直接计算的单台时间偏差与地震定位结果中的走时残差精度基本一致．

4.2   结论

本文是基于台站对互相关格林函数的走时差来直接计算单台的时间误差，是从记录数据中直接计算. 它不依赖于外部时钟的校正日志或真实的地震记录，并引入协方差矩阵来估计计算结果的置信水平和误差范围． 这对提高数字地震台网的时间系统精度具有重要的实际意义. 能够准实时地检测出地震观测系统中记录信号的明显时钟误差(＞3 s)，还可以通过准实时地计算台网中各个台站的平均时间偏移来消除时间系统的平均偏差，从而能够提高台网的绝对时间精度. 特别是当地震台站位于高纬度、 山区或海底时，其校正时间系统的实际效应将更加突显． 运用本文方法还可以对历史数据中的时钟误差进行校正．

另外，设想当台站对的间距进一步减小时，随着格林函数信噪比的提高，不仅可以提高单台时间误差的计算精度，还可以分辨出背景噪声源的趋势性变化．

衷心感谢审稿专家提出的宝贵意见，以及赵仲和研究员提供误差分析方面的文献资料．