饱和砂岩在温度和频率域的衰减和速度频散

席军; 宛新林; 周城光; 杜赟; 席道瑛

doi:10.3969/j.issn.0253-3782.2013.06.014

饱和砂岩在温度和频率域的衰减和速度频散

席军^1, ,,
宛新林²,
周城光³,
杜赟⁴,
席道瑛⁴

1.
中国北京 102617 北京石油化工学院机械工程学院
2.
中国合肥 230601 安徽建筑工业学院土木工程学院
3.
中国北京 100190 中国科学院噪声与振动重点实验室
4.
中国合肥 230026 中国科学技术大学地球和空间科学学院, 蒙城地球物理国家野外观测站

基金项目: 国家自然科学基金项目(40874093)资助.

详细信息

通讯作者:
席军, e-mail:xijun@bipt.edu.cn

中图分类号: P315.3⁺1
计量
- 文章访问数: 535
- HTML全文浏览量: 242
- PDF下载量: 8
出版历程
- 收稿日期: 2012-06-21
- 修回日期: 2013-09-01
- 发布日期: 2013-10-31

Attenuation and dispersion of saturated rocks in temperature and frequency domains

1.
School of Mechanical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, China
2.
The Civil Engineering School, Anhui University of Architecture, Hefei 230601, China
3.
Key Laboratory of Noise and Vibration Research, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China
4.
4) Mengcheng National Geophysical Observatory, School of Earth and Space Science, University of Science and Technology of China, Hefei 230026, China

摘要

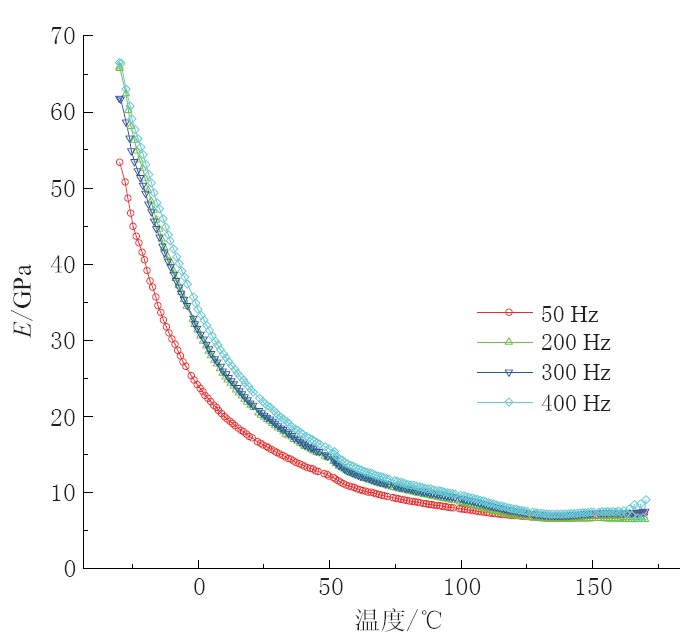
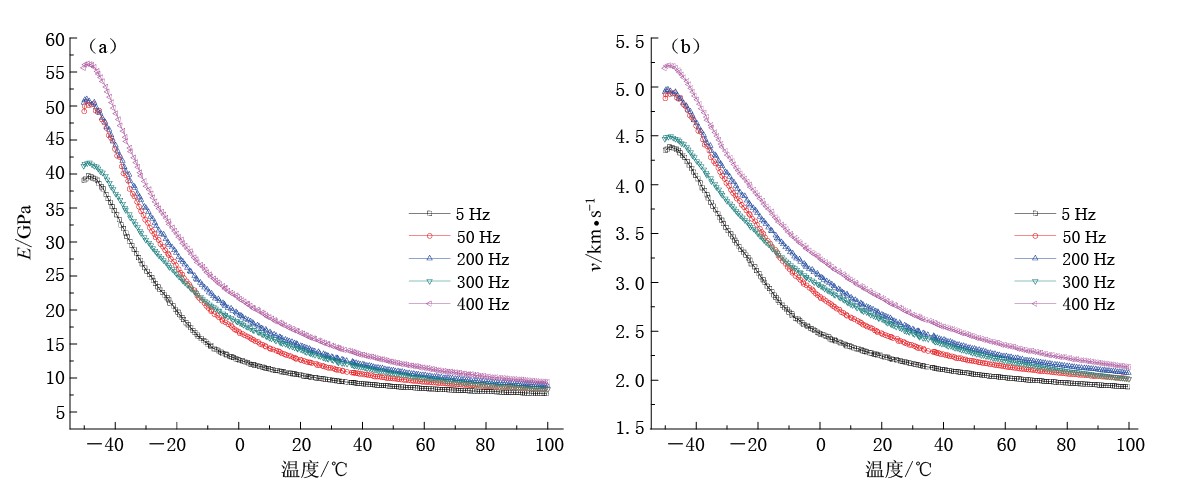
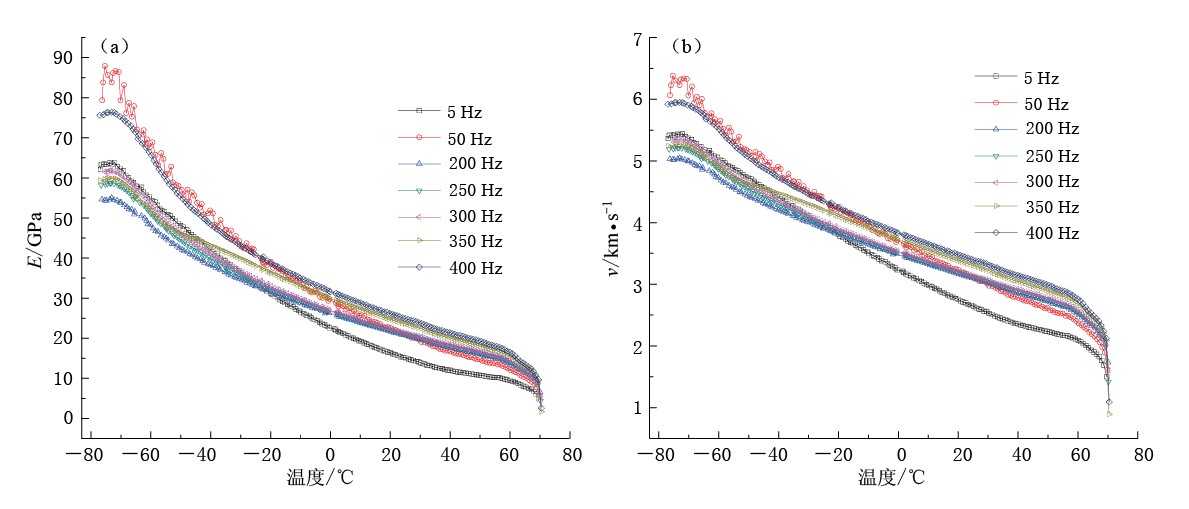
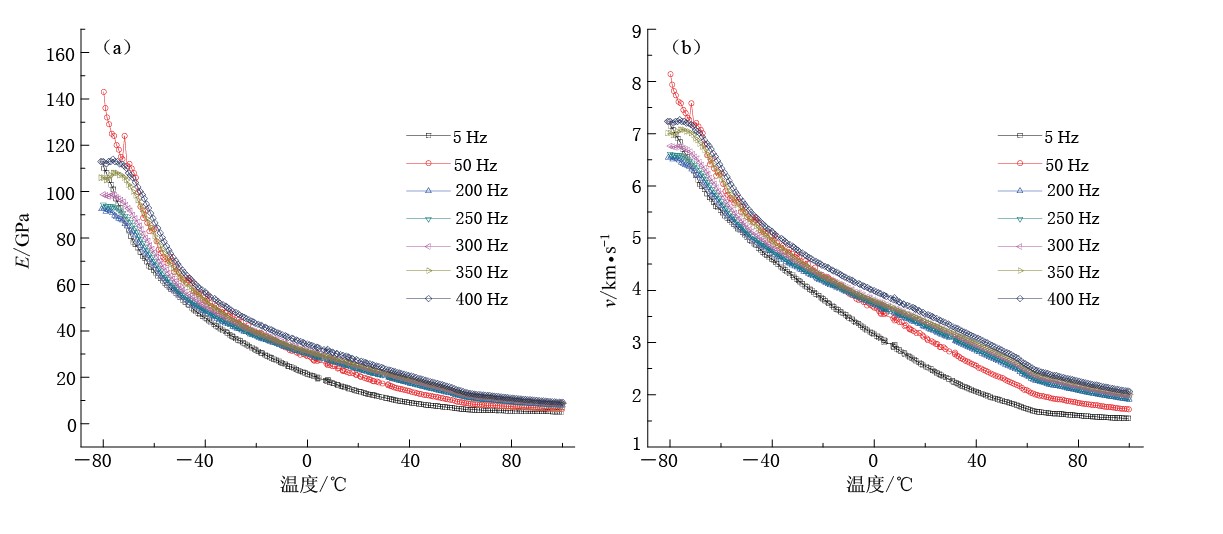
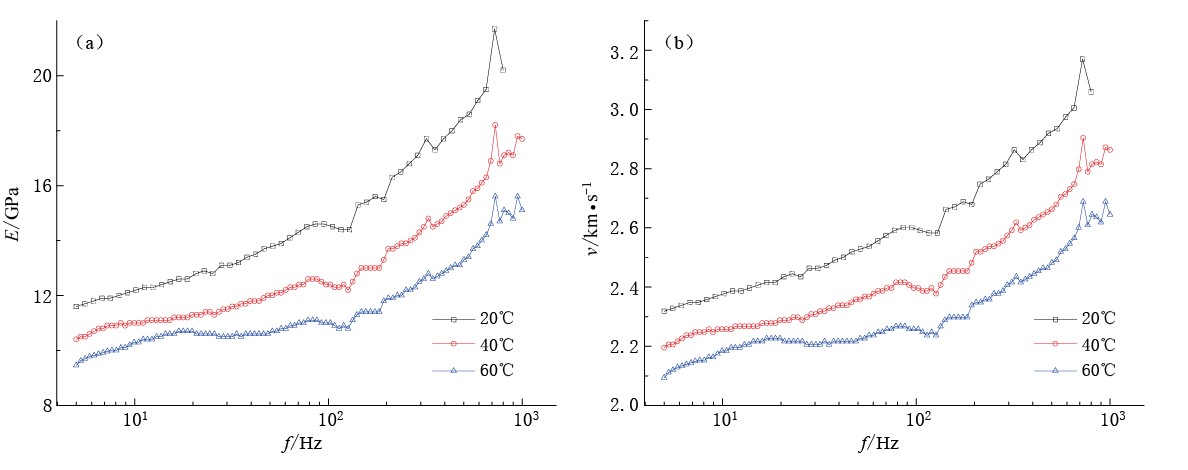
摘要: 利用Metravib热机械分析仪，在天然地震的频率和温度范围内，首次对泵油和甘油饱和两种孔隙度的彭山砂岩的衰减和速度频散进行了实验研究．结果表明， ① 泵油饱和彭山砂岩对频率和温度的依赖呈热激活弛豫规律； ② 杨氏模量和弹性波速度与孔隙度、温度呈负相关，与饱和液体的黏滞系数、频率呈正相关; ③ 频散效应因频率上升而增强，因温度增高而减弱．这一规律性的结果为地震波理论研究提供了实验基础．
- 饱和砂岩 /
- 衰减 /
- 模量 /
- 速度频散
Abstract: Experiments are performed by Metravib dynamic mechanical analyzer about the attenuation and dispersion of pump-oil and glycerol saturated Peng-shan sandstones with two kinds of porosities. The frequency and temperature of tests are natural earthquake. The results show: ① The attenuation peak of pump-oil saturated Pengshan sandstone appears to be thermo-activated relaxation. ② Young’s modulus and elastic wave velocity of saturated Pengshan sandstones reduce with porosity and temperature increasing, and rise with viscosity coefficient of saturated liquid and frequency increasing. ③ Frequency dispersion attenuates as temperature increases, enhances as frequency rises. The data provides the experiment foundation for theoretical research of seismic waves.
- saturated rock /
- attenuation /
- modulus /
- dispersion of velocity

HTML全文

图 1 泵油饱和彭山砂岩PⅡ -14-2 (孔隙度17.07%)衰减随温度的变化

Figure 1. Attenuation vs. temperature for pump-oil saturated Pengshan sandstone PⅡ -14-2 (porosity 17.07%)

下载: 全尺寸图片幻灯片

图 2 泵油饱和自贡长石砂岩A-1的杨氏模量(E)随温度的变化

Figure 2. Young’s modulus (E) vs. temperature for pump-oil saturated Zigong arkosic sandstone A-1

下载: 全尺寸图片幻灯片

图 3 泵油饱和彭山砂岩PⅡ -14(孔隙度17.07%)杨氏模量(E)(a)与弹性波速(v)(b)随温度的变化

Figure 3. Young’s modulus,E,(a) and elastic wave velocity (b) vs. temperature for pump-oil saturated Pengshan sandstone PⅡ -14 (porosity 17.07%)

下载: 全尺寸图片幻灯片

图 4 泵油饱和彭山砂岩PⅡ -15(孔隙度17.07%)杨氏模量(E)(a)与弹性波速(v)(b)随温度的变化

Figure 4. Young’s modulus,E,(a) and elastic wave velocity (b) vs. temperature for pump-oil saturated Pengshan sandstone PⅡ-15 (porosity 17.07%)

下载: 全尺寸图片幻灯片

图 5 泵油饱和彭山砂岩P Ⅰ -20(孔隙度16.08%)杨氏模量(E)(a)与弹性波速(v)(b)随温度的变化

Figure 5. Young’s modulus,E,(a) and elastic wave velocity (b) vs. temperature for pump-oil saturated Pengshan sandstone P Ⅰ -20 (porosity 16.08%)

下载: 全尺寸图片幻灯片

图 6 甘油饱和彭山砂岩GPⅠ -1(孔隙度16.08%)杨氏模量(E)(a)与弹性波速度(v)(b)随温度的变化

Figure 6. Young’s modulus,E,(a) and elastic wave velocity (b) vs. temperature for glycerol-oil saturated Pengshan sandstone GPⅠ -1 (porosity 16.08%)

下载: 全尺寸图片幻灯片

图 7 甘油饱和彭山砂岩GPⅡ -1(孔隙度17.07%)杨氏模量(E)(a)与弹性波速度(v)(b)随温度的变化

Figure 7. Young’s modulus,E,(a) and elastic wave velocity (b) vs. temperature for glycerol-oil saturated Pengshan sandstone GPⅡ -1 (porosity 17.07%)

下载: 全尺寸图片幻灯片

图 8 泵油饱和彭山砂岩PⅡ -26 (孔隙度17.07%)杨氏模量(E)(a)与弹性波速度(v)(b)随温度的变化

Figure 8. Young’s modulus,E,(a) and elastic wave velocity (b) vs. temperature for pump-oil saturated Pengshan sandstone PⅡ -26 (porosity 17.07%)

下载: 全尺寸图片幻灯片

图 9 泵油饱和彭山砂岩PⅡ -21(孔隙度17.07%)杨氏模量(E)(a)与弹性波速度(v)(b)随频率的变化

Figure 9. Young’s modulus,E,(a) and elastic wave velocity (b) vs. frequency for pump-oil saturated Pengshan sandstone PⅡ -21 (porosity 17.07%)

下载: 全尺寸图片幻灯片

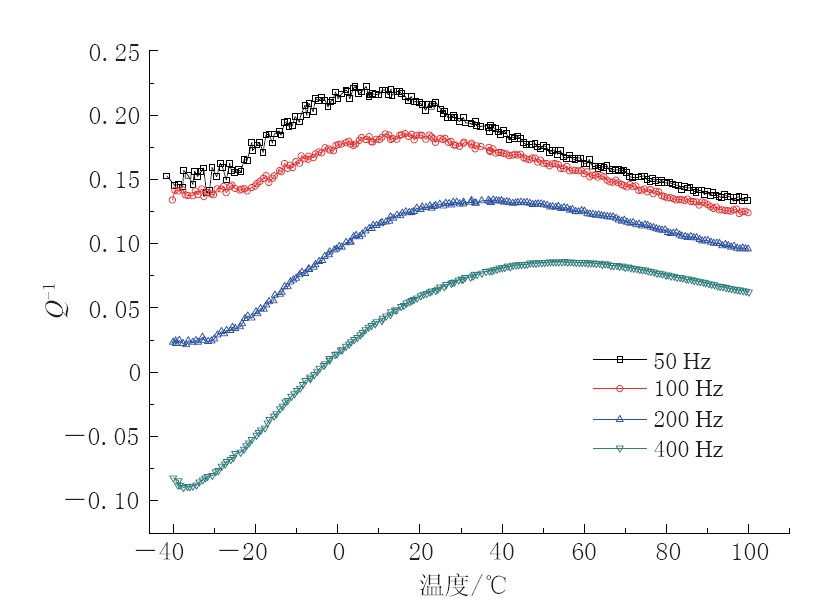
表 1 弛豫衰减峰的峰位和峰值强度

Table 1 The location and strength of the relaxed attenuation peak

频率/Hz	峰位温度/℃	1/Q峰值强度
50	6.5	0.22
100	17	0.18
200	36	0.13
400	57	0.08

下载: 导出CSV

表 2 在相同实验条件下泵油饱和不同孔隙度的彭山砂岩的杨氏模量(E)

Table 2 Young’s moduli of bump-oil saturated Penshan sandstones with different porosity on the same experiment condition

标本编号	孔隙度	E值(20 ℃各频率平均)/GPa	E总平均值 /GPa
A-1	12.84%	22.0	22.0
PⅠ -20	16.08%	14.0
PⅠ -11	16.08%	17.5
PⅠ -10	16.08%	22.0	17.8
PⅡ -15	17.07%	16.0
PⅡ -13	17.07%	14.0
PⅡ -14	17.07%	19.5	16.5

下载: 导出CSV

参考文献(20)

杜赟 , 席道瑛, 徐松林, 易良坤. 2009. 多孔岩石波传播的热弛豫模型修正[J]. 地球物理学报, 52 (12): 3051-3060.

葛瑞, 塔潘, 杰克, 德沃金(编著). 1998. 徐海滨戴建春(译). 2008. 岩石物理手册: 孔隙介质中地震分析工具[M]. 合肥: 中国科学技术大学出版社: 166-171.

葛庭燧. 2000. 固体内耗理论基础-晶界弛豫与晶界结构[M].北京: 科学出版社: 29.

席道瑛, 徐松林, 席军, 易良坤, 杜赟. 2011. 饱和砂岩的粘弹行为的实验研究[J]. 地球物理学报, 54 (9): 2302-2308.

席道瑛, 周城光, 徐松林, 杜赟, 席军. 2012. 饱和砂岩滞弹性弛豫衰减机理的探索[J]. 地球物理学报, 55 (7): 2362-2370.

Batzle M, Wang Z J. 1992. Seismic properties of pore fluids[J]. Geophysics, 57 (11): 1396-1408.

Batzle M, Hofmann R, Han D H, Castagna J. 2001. Fluids and frequency dependent seismic velocity of rocks[J]. The Leading Edge, 20 (2): 168-171.

Batzle M L, Han D H, Hofmann R. 2006. Fluid mobility and frequency-dependent seismic velocity: Direct measurements[J]. Geophysics, 71 (1): N1-N9, doi:10.1190/1.2159053.

Dvorkin J, Nur A. 1993. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms[J]. Geophysics, 58 (4): 524-533.

Gist G A. 1994a. Interpreting laboratory velocity measurements in partially gas-saturated rocks[J]. Geophysics, 59 (7): 1100-1109.

Gist G A. 1994b. Fluid effect on velocity and attenuation in sandstone[J]. J Acoust Soc Am, 96 (2): 1158-1173.

Kan T K, Batzle M L, Gaiser J E. 1983. Attenuation measured from VSP: Evidence of frequency-dependent Q[C]//Proceedings of the 53rd SEG Meeting. Las Vegas, USA: 589-590.

Messner R. 1983. Attenuation of seismic waves in sediments[C]//Proceedings of the 11th World Petroleum Congress. London: 363-381.

Pennington W D. 1997. Seismic petrophysics: An applied science for reservoir geophysics[J]. The Leading Edge, 16 (3): 241-246.

Pride S R, Harris J M, Johnson D L, Mateeva A, Nihei K T, Nowack R L, Rector J W, Spetzler H, Wu R, Yamomoto T, Berryman J G, Fehler M. 2003. Permeability dependence of seismic amplitudes[J]. The Leading Edge, 22 (6): 518-525.

Spencer J W. 1981. Stress relaxation at low frequencies in fluid-saturated rocks: Attenuation and modulus dispersion[J]. J Geophys Res, 86 (B3): 1803-1812.

Xi D Y, Liu B, Liu W, Yi L K. 2000. The dependence relationship of relaxation attenuation on time and temperature of saturated rocks[J]. Chinese J Geophys, 43 (6): 873-880.

Xi D Y, Liu B, Tian X Y. 2002. Anisotropy and nonlinear viscoelastic behavior of saturated rocks[J]. Chinese J Geophys, 45 (1): 101-111.

Xi D Y, Liu X Y, Zhang C Y. 2007. The frequency (or time)-temperature equivalence of relaxation in saturated rocks[J]. Pure Appl Geophys, 164 (11): 2157-2173.

Xi D Y, Xu S L, Du Y, Yi L K. 2011. Wave propagation analysis of porous rocks with thermal activated relaxation mechanism[J]. J Appl Geophys, 73 (3): 289-303.