Sensitivity analysis on maximum tsunami wave heights to the potential tsunami source parameters based on extended FAST method
-
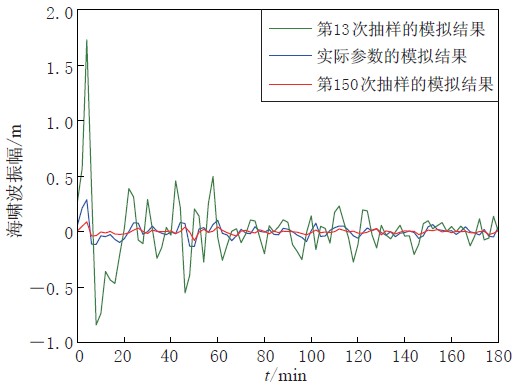
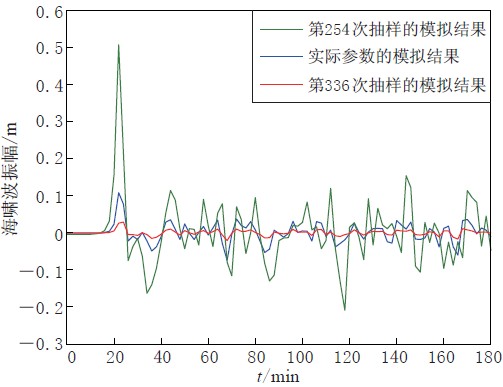
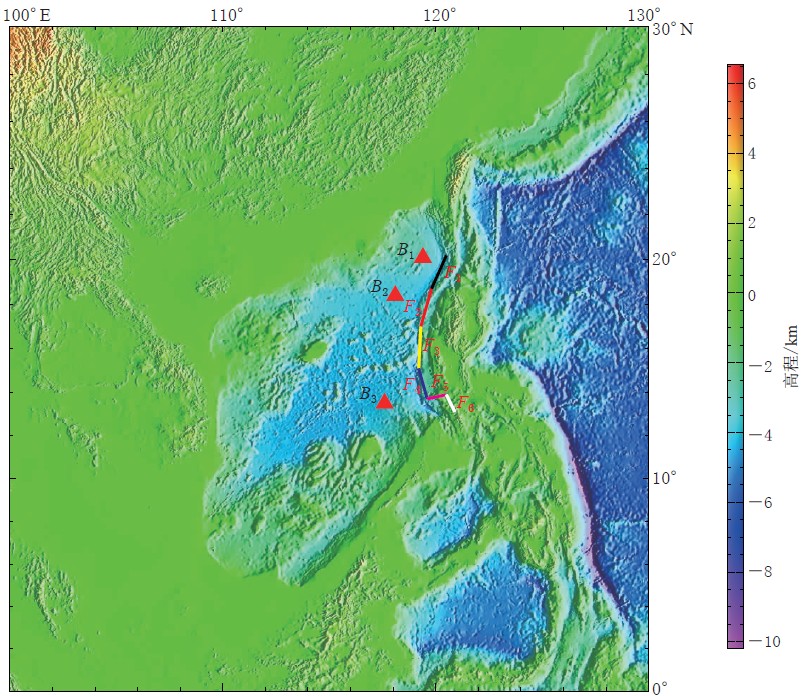
摘要: 以马尼拉海沟的北断层发生MW8.0地震在南海引发海啸为假想的模拟情景, 利用E-FAST法定量分析了COMCOT海啸数值模型输出(最大海啸波高)对震级, 震源深度, 震中位置和断层走向、 倾角、 滑动角等震源参数的敏感性, 以及各震源参数间的交互效应对最大海啸波高的影响. 结果表明, 观测点B1( 20.1°N, 119.4°E)、 B2(18.4°N, 118.1°E)和B3(13.5°N, 117.6°E)的最大海啸波高都对震级十分敏感, 对震中位置、 断层走向和倾角较为敏感. 敏感的震源参数在影响上述3个观测点的最大海啸波高时, 与其它震源参数产生了较强的交互效应. 但是对于不同的观测点, 各震源参数的重要度排序则存在一定的差异. 该分析结果有助于更好地认识海啸波高与潜在海啸源参数之间的关系.Abstract: Using extended FAST method, we quantitatively analyze the sensitivity of maximum tsunami wave heights to the seismic tsunami source parameters, on the assumption that an earthquake with magnitude MW8.0 occurred at the northern fault segment along Manila Trench and triggered a tsunami in the South China Sea. The tsunami wave heights are computed based on the COMCOT model, and the investigated parameters are principally the earthquake’s magnitude, focal depth, epicentral location, strike angle, dip angle and rake angle. We also analyze the interaction effects of the above parameters on the maximum tsunami wave heights. The results of the sensitivity analysis indicate that the maximum tsunami wave heights of B1(20.1°N, 119.4°E), B2(18.4°N, 118.1°E), B3(13.5°N, 117.6°E) are very sensitive to the earthquake magnitude, followed by the epicentral location, the strike angle and the dip angle. The interaction effects between the sensitive parameters are rather strong. But there exist differences in each parameter’s important measure order for different locations. Our result is significant to understanding the relationship between the tsunami wave heights and the seismic tsunami source parameters.
-
Keywords:
- sensitivity analysis /
- numerical simulation /
- source parameter /
- tsunami
-
-
表 1 震源参数服从的概率分布
Table 1 Probability distribution of the earthquake parameters

表 2 观测点B1, B2和B3的最大海啸波高对各震源参数的主效应指标和全效应指标
Table 2 Total and first-order effects of the maximum tsunami wave heights on the source parameters at the sites B1, B2 and B3

-
孟玉梅, 赵永, 王斌. 2001. 中国地震观测台网地震速报定位偏差的分析[J]. 地震, 21(3): 65-69. Meng Y M, Zhao Y, Wang B. 2001. The analysis on deviation of rapid location by China Seismic Observational Network[J]. Earthquake, 21(3): 65-69 (in Chinese).
任鲁川, 薛艳, 简春林, 冯尉. 2009. 南海北缘海啸波高对潜在海啸源震级测量偏差的敏感性[J]. 中国地震, 25(2): 186-192. Ren L C, Xue Y, Jian C L, Feng W. 2009. Sensitivity analysis of the effect of the earthquake magnitude in potential tsunami source on the tsunami wave amplitude in the northern area of the South China Sea[J]. Earthquake Research in China, 25(2): 186-192 (in Chinese).
任枭, 刘瑞峰, 陈运泰. 2006. 一种快速测定大地震震级的方法[J]. 地震地磁观测与研究, 27(1): 107-110. Ren X, Liu R F, Chen Y T. 2006. A strategy to rapidly determine the magnitude of great earthquakes[J]. Seismological and Geomagnetic Observation and Research, 27(1): 107-110 (in Chinese).
王淑贞, 郭履灿. 1988. 震级偏差稳定性的研究及检验方法的应用[J]. 东北地震研究, (1): 35-42. Wang S Z, Guo L C. 1988. On the stability of magnitude deviation and application of examination method[J]. Seismological Research of Northeast China, (1): 35-42 (in Chinese).
姚远, 蔡树群, 王盛. 2007. 海啸波数值模拟的研究现状[J]. 海洋科学进展, 25(4): 489 -494. Yao Y, Cai S Q, Wang S. 2007. Present status of study on numerical simulation of tsunami wave[J]. Advances in Marine Science, 25(4): 489-494 (in Chinese).
叶琳, 于福江, 吴玮. 2005. 我国海啸灾害及预警现状与建议[J]. 海洋预报, 22(增刊): 147-151. Ye L, Yu F J, Wu W. 2005. The disaster and warning of tsunami in China and the suggestion in future[J]. Marine Forecasts, 22(Suppl.): 147-151 (in Chinese).
张晁军, 张晓东, 苗春兰, 丁秋琴, 张爱武. 2010. 近震震源深度测定精度的理论误差分析[J]. 中国地震, 26(2): 156-163. Zhang C J, Zhang X D, Miao C L, Ding Q Q, Zhang A W. 2010. The analysis of the theoretical error of the accuracy of measuring the focal depth of near earthquake[J]. Earthquake Research in China, 26(2): 156-163 (in Chinese).
赵荣国, 李卫平. 1997. 现今震级测定偏差[J]. 国际地震动态, (12): 1-8. Zhao R G, Li W P. 1997. Deviations in magnitude determination at present day[J]. Recent Developments in World Seismology, (12): 1-8 (in Chinese).
赵荣国, 李卫平. 1998. 从震级偏差看震级问题[J]. 国际地震动态, (4): 10-16. Zhao R G, Li W P. 1998. Viewing magnitude problem from magnitude deviation[J]. Recent Developments in World Seismology, (4): 10-16 (in Chinese).
Cukier R I, Fortuin C M, Shuler K E, Petschek A G, Schaibly J H. 1973. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I: Theory[J]. J Chem Phys, 59: 3873-3878.
Cukier R I, Levine H B, Shuler K E. 1978. Nonlinear sensitivity analysis of multi-parameter model systems[J]. Journal of Computational Physics, 26: 1-42.
Dao M H, Tkalich P. 2007. Tsunami propagation modeling: A sensitivity study[J]. Nat Hazards Earth Syst Sci, 7: 741-754.
Gica E, Teng M, Liu P L F, Titov V, Zhou H. 2007. Sensitivity analysis of source parameters for earthquake-generated distant tsunamis[J]. J Waterway, Port, Coastal, Ocean Eng, 133(6): 429-441.
Geist E L. 1999. Local tsunamis and earthquake source parameters[J]. Advances in Geophysics, 39: 117-198.
Grilli S T, Ioualalen M, Asavanant J, Shi F Y, Kirby J T, Watts T. 2007. Source constraints and model simulation of the December 26, 2004 Indian Ocean tsunami [J]. J Waterway, Port, Ocean Coastal Eng, 133(6): 414-428.
Hanks T C, Kanamori H. 1979. A moment-magnitude moment scale[J]. J Geophys Res, 84: 2348-2350.
Imamura F, Imteaz M A. 1995. Long waves in two layer governing equations and numerical model[J]. Journal of Science of Tsunami Hazards, 13: 3-24.
Kirby S, Geist E L, Lee W H K, Scholl D, Blakely R. 2006. Tsunami Source Characterization for Western Pacific Subduction Zones: A Preliminary Report[R/OL]. [2012-10-15]. http://walrus.wr.usgs.gov/tsunami/workshop/.
Liu P L F, Woo S B, Cho Y S. 1998. Computer Programs for Tsunami Propagation and Inundation[CP/OL]. [2012-06-01]. http://ceeserver.cee.cornell.edu/pll-group/comcot.htm.
Liu P L F, Wang X, Andrew J S. 2007. Tsunami Hazard and Forecast Study in South China Sea[R/OL]. [2012-06-01]. http://ceeserver.cee.cornell.edu/pll-group/doc/Prototype_Tsunami_early_warning_SCS1.pdf.
Myers E P, Baptista A M. 2001. Inversion for tides in the Eastern North Pacific Ocean[J]. Advance in Water Resources, 24(5): 505-519.
Okal E A, Synolakis C E. 2008. Far-field tsunamis hazard from mega-thrust earthquakes in the Indian Ocean [J]. Geophys J Int, 172: 995-1015.
Saltelli A, Tarantola S, Chan K. 1999. A quantitative model-independent method for global sensitivity analysis of model output[J]. Technometrics, 41(1): 39-56.
Seda Y, Tuncay T. 2010. Sensitivity analysis on relations between earthquake source rupture parameters and far-field tsunami waves: Case studies in the eastern Mediterranean region Turkish[J]. Earth Sci, 19: 313-349.
Shuto N.1991. Numerical simulation of tsunamis: Its present and near future[J]. Nat Hazards, 4(2/3): 171-191.
Sobol I M. 1993. Sensitivity analysis for nonlinear mathematical models[J]. Mathematical Modeling & Computational Experiment, 1: 407-414.
Synolakis C, Liu P L F, Carrier G, Yeh H. 1997. Tsunamigenic sea-floor deformations[J]. Science, 278: 598-600.
Titov V V, Gonzalez F I. 1997. Implementation and Testing of the Method of Splitting Tsunami Model (MOST)[R/OL]. [2012-10-20]. www.pmel.noaa.gov/pubs/PDF/tito1927/tito1927.pdf
Titov V V, Mofjeld H O, González F I, Newman J C. 2001. Offshore forecasting of Alaskan tsunamis in Hawaii[C]//Tsunami Research at the End of a Critical Decade. Birmingham, England: Kluwer Acad Pub: 75-90.
USGS Tsunami Sources Workshop. 2006. Great Earthquake Tsunami Sources: Empiricism & Beyond[R/OL]. [2012-10-10]. http://walrus.wr.usgs.gov/tsunami/workshop/.
Wang X, Liu P L F. 2007. A numerical investigation of Boumerdes-Zemmouri (Algeria) earthquake and tsunami[J]. Computer Modeling in Engineering & Sciences, 10(6): 171-183.
Wells D L, Coppersmith K J. 1994. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement[J]. Bull Seismol Soc Am, 84(4): 974-1002.




 下载:
下载: