Born approximation paradox of linear finite-frequency theory
-
摘要: 对有限频率层析成像线性理论的波恩近似问题进行梳理, 用数值方法统计分析其适用范围, 结果表明波恩近似要求最大速度扰动不超过1%; 然后对相关走时一阶近似进行统计分析, 结果表明它也只适用于最大速度扰动在1%以内的情形. 然而, 结合波恩近似和相关走时一阶近似而得到的有限频率线性理论, 其适用的速度扰动范围最大可达10%. 这个表面上的逻辑悖论, 称为“波恩近似佯谬”. 此佯谬是由于不恰当地使用波恩近似造成的. 本文摒弃波恩近似, 使用泛函的Fréchet微分和隐函数定理推导得到有限频率线性理论, 圆满解释了波恩近似佯谬. 由于有限频率非线性理论早已摒弃了波恩近似, 因此波恩近似概念在有限频率层析成像理论中完全没有必要.Abstract: After reviewing the Born approximation problem of linear finite-frequency tomography theory, its scope of application is statistically analyzed by numerical method. The result indicates that the maximum velocity perturbation should not exceed 1% for Born approximation. Then the statistical analyses on the first-order approximation of cross-correlation travel-time also show that it only meets the case of the maximum velocity perturbation less than 1%. However, the maximum velocity perturbation can be 10% for linear finite-frequency theory, which combines Born approximation with the first-order approximation of cross-correlation travel-time. This apparent logic paradox is called “Born approximation paradox”, which is caused by misusage of Born approximation. Thus, Born approximation is discarded in this study; Fréchet derivative and implicit functional theorem are used to deduce linear finite-frequency theory. As a result, Born approximation paradox is explained thoroughly. Since Born approximation has been discarded early in nonlinear finite-frequency theory, this concept is unnecessary in finite-frequency tomography theory.
-
-
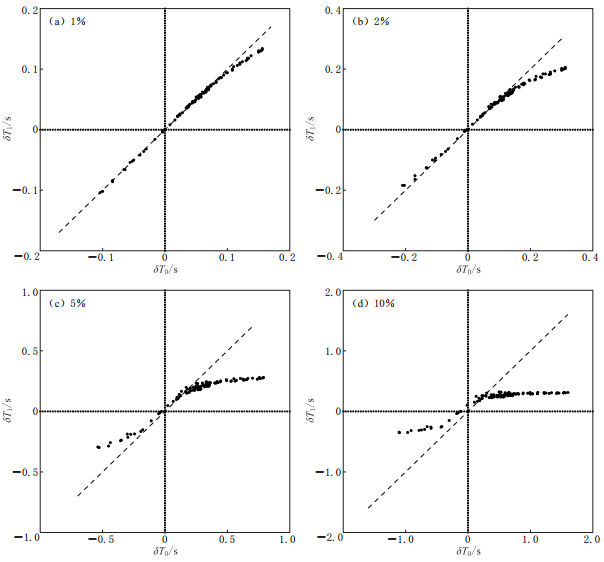
图 2 随机扰动情形下的波恩近似相关走时误差
初始模型为均匀介质,目标模型为高斯型三维随机介质. 图(a)—(d)的最大速度扰动分别为1%,2%,5%和10%
Figure 2. The errors of cross-correlation traveltime of Born approximation with random perturbations The starting model is homogeneous medium.
The object model is 3-D Gaussian random medium. The maximum velocity perturbations of Figs.(a)—(d) are 1%,2%,5% and 10%,respectively
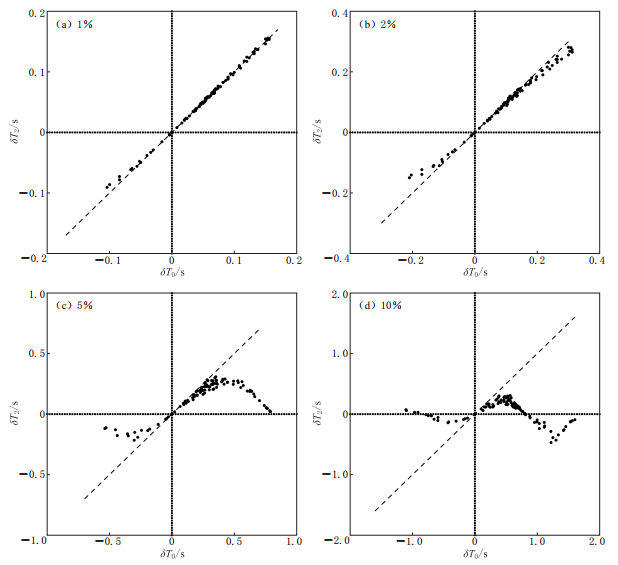
图 3 随机扰动情形下相关走时泛函的一阶近似误差
模型和震源参数同图2. 图(a)—(d)的最大速度扰动为分别为1%,2%,5%和10%
Figure 3. The first-order approximation errors of the cross-correlation traveltime functional with random perturbations
The parameters of the model and seismic sources are the same as those in Fig.2. The maximum velocity perturbations in Figs.(a)—(d) are separately 1%,2%,5% and 10%
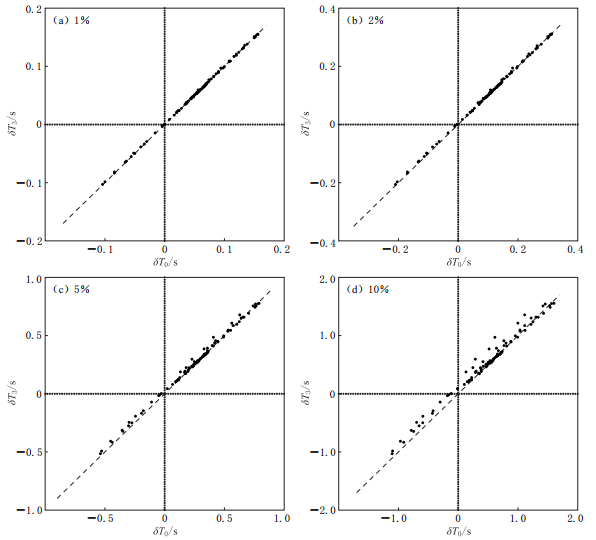
图 4 随机扰动情形下有限频率方法的相关走时误差
模型和震源参数同图2. 图(a)—(d)的最大速度扰动为分别为1%,2%,5%和10%
Figure 4. The errors of the cross-correlation traveltime of finite-frequency theory with random perturbations
The parameters of the model and seismic sources are the same as those in Fig.2. The maximum velocity perturbations in Figs.(a)—(d) are separately 1%,2%,5% and 10%
表 1 震源参数
Table 1 Focal parameters

表 2 接收点参数
Table 2 Receiver parameters

-
郭大钧. 2001. 非线性泛函分析[M]. 第2版. 济南: 山东科学技术出版社: 77-82. Guo D J. 2001. Nonlinear Functional Analysis[M]. 2nd ed. Ji'nan: Shandong Science and Technology Press: 77-82 (in Chinese).
Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods[M]. San Francisco: W H Freeman and Company: 721-751.
Baig A M, Dahlen F A. 2004. Statistics of traveltimes and amplitudes in random media[J]. Geophys J Int, 158(1): 187-210.
Baig A M, Dahlen F A, Hung S H. 2003. Traveltimes of waves in three-dimensional random media[J]. Geophys J Int, 153(2): 467-482.
Bezada M J, Levander A, Schmandt B. 2010. Subduction in the southern Caribbean: Images from finite-frequency P wave tomography[J]. J Geophys Res, 115(B12): B12333. doi:10.1029/2010JB007682.
Chen P, Zhao L, Jordan T H. 2007. Full 3D tomography for the crustal structure of the Los Angeles region[J]. Bull Seismol Soc Am, 97(4): 1094-1120.
Coates R T, Chapman C H. 1990. Ray perturbation theory and the Born approximation[J]. Geophys J Int, 100(3): 379-392.
Dahlen F A, Baig A M. 2002. Fréchet kernels for body-wave amplitudes[J]. Geophys J Int, 150(2): 440-466.
Dahlen F A, Hung S H, Nolet G. 2000. Fréchet kernels for finite-frequency traveltimes: I. Theory[J].Geophys J Int, 141(1): 157-174.
Fichtner A, Kennett B L N, Igel H, Bunge H P. 2008. Theoretical background for continental- and global-scale full-waveform inversion in the time-frequency domain[J]. Geophys J Int, 175(2): 665-685.
Fichtner A, Kennett B L N, Igel H, Bunge H P. 2010. Full waveform tomography for radially anisotropic structure: New insights into present and past states of the Australasian upper mantle[J]. Earth Planet Sci Lett, 290(3/4): 270-280.
Frankel A. 1986. Finite difference simulations of seismic scattering: Implications for the propagation of short-period seismic waves in the crust and models of crustal heterogeneity[J]. J Geophys Res, 91(B6): 6465-6489.
Gautier S, Nolet G, Virieux J. 2008. Finite-frequency tomography in a crustal environment: Application to the western part of the Gulf of Corinth[J]. Geophys Prospect, 56(4): 493-503.
Gee L S, Jordan T H. 1992. Generalized seismological data functionals[J]. Geophys J Int, 111(2): 363-390.
Graves R W. 1996. Simulation seismic wave propagation in 3D elastic media using staggered-grid finite differences[J]. Bull Seismol Soc Am, 86(4): 1091-1085.
Hudson J A. 1977. Scattered waves in the coda of P[J]. J Geophys, 43(1/2): 359-374.
Hung S H, Garnero E J, Chiao L Y, Kuo B Y, Lay T. 2005. Finite frequency tomography of D″ shear velocity heterogeneity beneath the Caribbean[J]. J Geophys Res, 110(B7): B07305. doi:10.1029/2004JB003373.
Hung S H, Chen W P, Chiao L Y. 2011. A data-adaptive, multiscale approach of finite-frequency, traveltime tomography with special reference to P and S wave data from central Tibet[J]. J Geophys Res, 116(B6): B06307. doi:10.1029/2010JB008190.
Knopoff L. 1959. Scattering of compression waves by spherical obstacles[J]. Geophysics, 24(1): 30-39.
Liang X F, Shen Y, Chen Y J, Ren Y. 2011. Crustal and mantle velocity models of southern Tibet from finite frequency tomography[J]. J Geophys Res, 116(B2): B02408. doi:10.1029/2009JB007159.
Liu K J, Levander A, Niu F L, Miller M S. 2011. Imaging crustal and upper mantle structure beneath the Colorado Plateau using finite frequency Rayleigh wave tomography[J]. Geochem Geophy Geosy, 12(7): Q07001. doi:10.1029/2011GC003611.
Liu Q Y, Tromp J. 2006. Finite-frequency kernels based on adjoint methods [J]. Bull Seismol Soc Am, 96(6): 2383-2397.
Luo Y, Schuster G T. 1991. Wave-equation traveltime inversion[J]. Geophysics, 56(5): 645-653.
Miles J W. 1960. Scattering of elastic waves by small inhomogeneities[J]. Geophysics, 25(3): 642-648.
Montelli R, Nolet G, Dahlen F A, Masters G, Engdahl E R, Hung S H. 2004. Finte-frequency tomography reavels a variety of plumes in the mantle[J]. Science, 303(5656): 338-343.
Rayleigh B, Strutt J W. 1945. The Theory of Sound[M]. New York: Dover Publications: 415-421.
Snieder R. 1986. 3-D linearized scattering of surface waves and a formalism for surface wave holography[J]. Geophys J Int, 84(3): 581-605.
Tape C, Liu Q Y, Maggi A, Tromp J. 2009. Adjoint tomography of the southern California crust[J]. Science, 325: 988-992.
Tape C, Liu Q Y, Maggi A, Tromp J. 2010. Seismic tomography of the southern California crust based on spectral-element and adjoint methods [J]. Geophys J Int, 180(1): 433-462.
Tromp J, Tape C, Liu Q Y. 2005. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels[J]. Geophys J Int, 160(1): 195-216.
Wolf A. 1945. Motion of a rigid sphere in an acoustic wave field[J]. Geophysics, 10(1): 91-109.
Wu R, Aki K. 1985. Scattering characteristics of elastic waves by an elastic heterogeneity[J]. Geophysics, 50(4): 582-595.
Yamakawa N. 1956. Investigation of the disturbance produced by spherical obstacles on elastic waves (I)[J]. Quart J Seism, 21(1): 1-12.
Yang T, Shen Y, van der Lee S, Solomon S C, Hung S H. 2006. Upper mantle structure beneath the Azores hotspot from finite-frequency seismic tomography[J]. Earth Planet Sci Lett, 250(1/2): 11-26.
Zhang W, Chen X F. 2006. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J]. Geophys J Int, 167(1): 337-353.
Zhang W, Zhang Z G, Chen X F. 2012. Three-dimensional elastic wave numerical modeling in the presence of surface topography by a collocated-grid finite-difference method on curvilinear grids[J]. Geophys J Int, 190(1): 358-378.
Zhao L, Jordan T H, Chaptman C H. 2000. Three-dimensional Fréchet differential kernels for seismic delay time[J]. Geophys J Int, 141(3): 558-576.
Zhao L, Jordan T H, Olsen K B, Chen P. 2005. Fréchet kernels for imaging regional earth structure based on three-dimensional reference models[J]. Bull Seismol Soc Am, 95(6): 2066-2080.




 下载:
下载: