Energy magnitude determination of moderate-strong earthquakes
-
摘要: 本文根据地震波衰减特性，开展了利用宽频带地震波形数据测定地震波能量ES和能量震级Me的方法研究。利用震中距处于20°—98°范围内的宽频带远震P波波形数据，测定了4次国外和4次国内中强震的能量震级Me，并对其面波震级MS、矩震级MW及能量震级Me进行了分析对比。结果表明：面波震级MS表示的是地震在某一固定频率所辐射的地震波能量大小；矩震级MW与地震所产生的断层长度、断层宽度、震源破裂的平均位错量等静态构造效应密切相关；而能量震级Me反映的是震源动态特征，与地震震源的动力学特性密切相关。由于地震是以地震波形式辐射，能量主要集中在震源谱的拐角频率附近，因此能量震级Me更适合描述地震的破坏性。由此可见，联合测定面波震级MS，矩震级MW和能量震级Me对于地震定量研究以及地震灾害与风险评估具有重要作用。
-
关键词:
- 地震波能量 /
- 能量震级 /
- 宽频带远震P波波形数据 /
- 震源动态特征 /
- 震源谱
Abstract: This paper, based on the seismic wave attenuation characteristics, explores a method for utilizing broadband seismic waveform data to measure seismic energy ES and energy magnitude Me. The energy magnitudes Me of four overseas and four domestic moderate-strong earthquakes are measured by using broadband teleseismic P waveform data with epicentral distance in the range of 20°−98°. The comparison of surface wave magnitude MS, moment magnitude MW and energy magnitude Me of several earthquakes shows that: surface wave magnitude MS represents the magnitude of the energy of seismic wave radiating at a fixed frequency; the moment magnitude MW is closely related to the static structural effects such as the length of fault, the width of fault and the average dislocation amount of the source rupture produced by the earthquake; the energy magnitude Me reflects source dynamic characteristics and is closely related to the dynamic characteristics of the seismic source. The energy radiated by the earthquake in the form of seismic waves is mainly concentrated near the corner frequency of the source spectrum, so the energy magnitude Me is more suitable to describe the destructiveness of the earthquake. Therefore, joint determination of surface wave magnitude MS, moment magnitude MW and energy magnitude Me are of great significance for quantifying and evaluating the disasters caused by earthquakes or tsunamis. -
引言
自1935年里克特提出震级的概念（Richter，1935）以来，地震辐射能量一直是地震科学家很重视却不能精确测定的参数。传统的地震学研究中，通常是根据一定的理论或经验模式，通过地震震级来估计地震能量。Gutenberg和Richter （1954）得到了面波震级MS与地震能量ES之间的关系为
$\lg {E_{\rm S}} {\text{＝}} 1.5{M_{\rm{S}} } {\text{＋}} 4.8{\text{，}}$
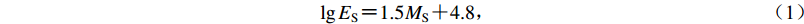
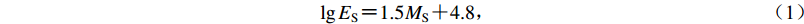
(1) 这就是著名的古登堡-里克特震级-能量关系式，式中ES的单位是J。值得注意的是，利用震级与地震能量之间的经验关系来估计地震能量具有一定的局限性，仅仅是对地震能量的粗略估计。震级是针对较窄频段的地震波的测定结果，例如：测定短周期体波震级一般使用周期为1 s左右的地震体波信号，测定面波震级一般是使用20 s左右周期的面波信号，而地震能量的测定则应考虑所有频段的地震波能量。因此，从频率域来看，用震级来推算地震能量，结果并不十分严谨、准确。数字地震学的发展使得我们可以直接使用数字地震观测资料来测定地震能量ES和能量震级Me，这样得到的结果也更加可靠（Kanamori et al，1993；Choy，Boatwright，1995）。
从1986年起，美国地质调查局（United States Geological Survey，简写为USGS）国家地震信息中心（National Earthquake Information Center，简写为NEIC）采用Boatwright和Choy （1986）的方法测定全球范围内MW＞5.5中强震的辐射能量，进而得到能量震级Me，测定结果在NEIC常规产出的 《震中初步报告》 中列出。NEIC将其测定结果在美国地震学研究联合会（Incorpor-ated Research Institutions for Seismology，简写为IRIS）的地震能量查询网站http://www.iris.edu/spud/eqenergy发布，供全球查询使用。德国国家地球科学研究中心（Helmholtz-Zentrum Potsdam-Deutsches Geo Forschungs Zentrum，简写为GFZ）也在积极研究地震能量和能量震级 ，Di Giacomo等（2008）提出浅源强震至浅源特大地震的能量震级Me的测定方法，利用20°—98°距离范围之内的宽频带远震P波信号，测定了浅源地震的辐射能量ES和能量震级Me，并通过61次浅源地震进行了验证。
近20年来，我国数字地震台网建设得到了迅速的发展，通过 “ 中国数字地震监测系统 ” 、 “ 中国数字地震观测网络 ” 和 “ 中国地震背景场探测 ” 等3个项目的实施，已经建成了由国家地震台网、区域地震台网和流动地震台网构成的数字地震观测系统。截至2014年12月，我国正式运行的数字地震台站已逾千个。我国数字地震台网的建设为快速测定地震能量ES和能量震级Me提供了丰富可靠的数据基础。
本文将利用参考地球模型AK135Q （Kennett et al，1995）和QSSP软件包 （Wang，1999）来计算球形地球的格林函数，采用GFZ的能量震级测定方法（Di Giacomo et al，2008）重新设计地震波能量ES和能量震级Me的测定软件，并利用国家地震台网和全球地震台网（global seismic network，简写为GSN）地震台站的宽频带地震波形数据，测定4次国外和4次国内中强震的地震波能量ES和能量震级Me，在此基础上进一步优化软件结构，利用震中距处于20°—98°范围内的宽频带远震P波波形数据快速测定M6.0以上地震的地震波能量ES和能量震级Me，以期为我国地震台网日常产出地震波能量ES和能量震级Me。
1. 能量震级测定方法
1.1 地震波能量ES
如何度量一次地震的大小，经历了一个较长的发展过程（陈培善，1990）。对于构造地震而言，岩层在大地构造应力的作用下产生应变，并不断积累应变能，应力一旦超过了岩石所能承受的极限，岩石即会突然破裂，或沿原破裂面滑动，释放大量能量，这就是地震成因的断层假说。地震发生时所释放的能量，大部分以机械能（岩石破裂和位移）和转换为热能的形式存在于震源区，一部分以地震波的形式向四面八方传播。以地震波形式传播的能量称为地震波辐射能量，也就是由地震波携带出来的那一部分能量，简称地震辐射能或地震波能量。地震时释放的能量不能直接测量，与地震波能量相比，二者并不相等，地震波能量仅占地震时所释放能量的很小一部分。然而，地震波能量却是唯一能用地震学方法测量的物理量，因此提到地震能量时，一般是指地震波能量。
地震波能量ES是震源的重要物理参数。根据Rudnicki和Freund （1981）的研究，ES取决于断裂过程中应力条件的变化：
${E_{\rm{S}}}{\rm{ {\text{＝}} }}\int_{{\rm{ - }}\infty }^\infty {\int_S {\left({{\rm{ - }}{{ {\sigma}} _{ij}}{{ {\gamma}} _j}{{\dot { u}}_i}} \right){\rm{d}}S{\rm{d}}t} }{\text{，}}$
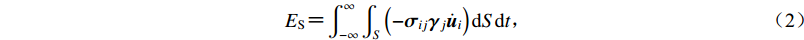
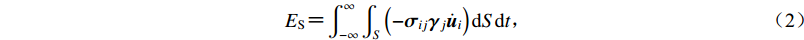
(2) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
${E_{\rm{S}}}{\rm{ {\text{＝}} }}\int_{{\rm{ - }}\infty }^\infty {\int_S {\rho \left({\alpha {{\dot u}_\alpha }^2 {\text{＋}} \beta {{\dot u}_\beta }^2} \right){\rm{d}}S{\rm{d}}t} }{\text{，}}$
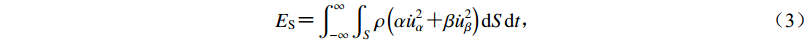
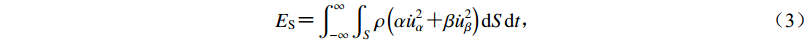
(3) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
${u_\alpha }\left(t \right) {\text{＝}} \frac{{{R_\alpha }\left({\theta{\text{，}}\phi } \right)}}{{4{\rm{{\text{π}} }}r{\alpha ^3}}}\dot M\left(t \right){\text{，}} {u_\beta }\left(t \right) {\text{＝}} \frac{{{R_\beta }\left({\theta{\text{，}}\phi } \right)}}{{4{\rm{{\text{π}} }}r{\beta ^3}}}\dot M\left(t \right){\text{，}} $
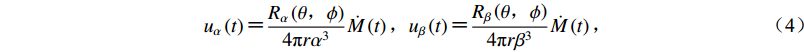
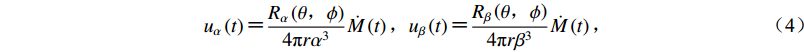
(4) 式中，Rα（θ，ϕ）和Rβ（θ，ϕ）分别为P波和S波的辐射场型，利用帕什瓦（Parseval）恒等式可以更容易地对频率域中的传播效应进行修正，最终可将ES的方程写成
$\begin{align} {E_S} {\text{＝}} \left({\frac{1}{{15{\text{π}}\rho {\alpha ^5}}} {\text{＋}} \frac{1}{{10{\text{π}}\rho {\beta ^5}}}} \right)\int_{ - \infty }^\infty {{{\left| {{\overset{\frown} {\ddot M}} \left(f \right)} \right|}^2}} {\rm{d}}f {\text{＝}} \left({\frac{2}{{15{\text{π}}\rho {\alpha ^5}}} {\text{＋}} \frac{1}{{5{\text{π}}\rho {\beta ^5}}}} \right)\int_0^\infty {{{\left| {{\overset{\frown} {\ddot M}} \left(f \right)} \right|}^2}{\rm{d}}f} {\text{≈}}\\ \left({\frac{2}{{15{\text{π}}\rho {\alpha ^5}}} {\text{＋}} \frac{1}{{5{\text{π}}\rho {\beta ^5}}}} \right)\int_{{f_1}}^{{f_2}} {{{\left| {{\overset{\frown} {\ddot M}} \left(f \right)} \right|}^2}{\rm{d}}f} {\text{，}}\hspace{70pt} \end{align} $
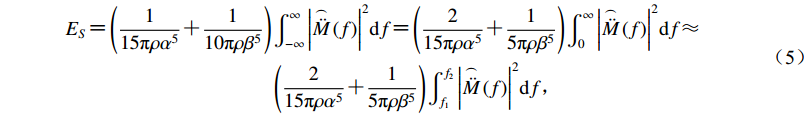
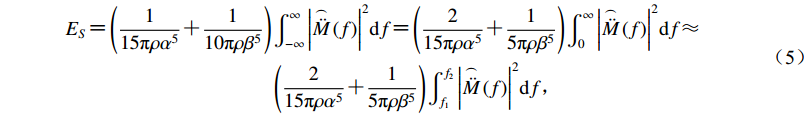
(5) 式中，f为频率，f1和f2为积分的上限和下限。理论上计算ES需要积分的上下限为0和∞，但是这在实际中是做不到的。下一小节中我们将讨论积分上下限的影响。式（5）中点源尺度远小于波长，那么方向性的影响可以忽略（Venkataraman，Kanamori，2004）。在这种情况下，通常只分析远震范围内记录到的地震波P波，因为相比于S波，P波有以下两大优势：其一，P波传播速度更快，会更早到达地震台，这对于快速测定地震震级至关重要；其二，P波会比S波更少受到传播中能量衰减的影响。
1.2 确定频率域积分上下限
式（4）中的积分上下限f1和f2会影响地震波能量ES和能量震级Me的计算。前人们已经对频率域计算能量震级的影响进行了深入研究（Di Bona，Rovelli，1988；Singh，Ordaz，1994；Ide，Beroza，2001），特别是，Ide和Beroza （2001）指出在ω−2模型中，地震波携带的80%地震能量均存在于高于拐角频率的高频部分。
理论上，积分的上下限应该涵盖全频段，然而，实际中要考虑地震波的频率范围，尤其要考虑高频成分。一般来说，P波时间窗tP限制频率域的下限f1，即f1≥1/tP。时间窗的长度应包括地震破裂的整个持续时间（震源动态破裂的时间），以避免时间窗饱和效应（Bormann et al，2007）。本文使用Bormann和Saul （2008，2009a，b）的技术估算持续时间，这种技术与Lomax等（2007）相似。该技术可以获得的持续时间是实际破裂持续时间的粗略估计（通常较大）。Di Giacomo等（2008）曾讨论过使用完整的S−P时间窗口是不实用的，这是因为使用如此长时间的窗口会包含后面的相位（比如PP和PPP），会导致能量震级结果偏高一点，偏高值不超过0.2 （Choy，Boatwright，2007）。另一方面，AK135Q模型中的Q结构是从最小周期为1 s的数据中得到（Montagner，Kennett，1996），那么高频极限f2＝1 Hz就确定了。
本文中积分上下限为f1＝12 mHz，f2＝1 Hz。尽管有上述的带宽限制，但是中强地震的拐角频率通常位于使用的频带内，那么源谱中不计算在内的部分（f＜f1或f＞f2）不会显著地影响能量震级Me的计算结果（最大误差不超过0.2）。不同研究人员采用不同的积分上下限f1和f2。例如，Choy和Boatwright （1995）使用的频段为10 mHz—5 Hz，Newman和Okal （1998）使用的频段为14 mHz—2 Hz。鉴于不同研究人员所研究的震级范围不同，其所选择的地震波频段也不相同。
1.3 对传播影响的修正
地震波能量ES的计算需要对观测到的频谱进行校正，使其在一个较宽的频率范围内进行几何扩展，此处还要考虑地震波从震源到接收器传播过程中所经历的频率衰减。这些波的传播现象决定了要恢复多少能量损失才能还原发震地点的状况。校正传播效应是地震学实践中最具挑战性的任务之一，这是由于与测定地震矩相比，还须考虑高频部分。此外，＞1 Hz的修正频率要求对地球的精细结构和衰减特性有详细的认知。因此，通常对震级M＞5.0且震中距大于20°的地震使用远震记录计算地震应力。通过建立一个均匀的一维层状结构来模拟大地滤波器的效果十分精确。Duda和Yanovskaya （1993）指出：由于地震波衰减与频率密切相关，要实现快速校正波的传播效应，必须计算出不同频率的振幅衰减谱函数。此外，对波的传播效应进行的校正必须适用于整个地球。为了满足这些要求，利用参考地球模型AK135Q（Kennett et al，1995；Montagner，Kennett，1996）和QSSP软件包（Wang，1999）来计算球形地球的格林函数。
与传统方法相比，采用数值模拟的优点在于，从已知的点源函数出发，可以考虑不同频率下的传播效应。计算震中距处于20°—35°之间的远震P波理论地震图时以1°为间隔，震中距为35°以上时以2.5°为间隔，这样区分是因为震中距介于20°—35°这个范围内时P波会受到上地幔和转换断层衰减的强烈影响。
1.4 能量震级Me
为了快速测定能量震级Me，对于震源深度h＜70 km的全球地震，仅考虑AK135Q模型的垂直异质性。为便于使用，以18 km深度为界限，将地震分为两组，并使用相应的α，β和ρ值给出均匀的一维AK135Q结构模型。对于震源深度在18 km以下的地震，取α＝6.8 km/s，β＝3.9 km/s，ρ＝2.92 g/cm3；对于震源深度在18 km以上的地震，取α＝8.035 5 km/s，β＝4.483 9 km/s，ρ＝3.641 g/cm3。而对于震源深度为18 km的处于边界上的地震，两套数据所测量的能量震级差别很小。对于h＜10 km的浅源地震，使用AK135Q模型计算能量震级得到的结果可能会偏大（不超过0.6震级单位）。将以上条件带入式（5）即可计算地震波能量ES。
Choy和Boatwright （1995）使用400多次地震的资料，导出了新的ES与Me的经验关系式：
$\lg {E_{\rm{S}}}{\rm{ {\text{＝}} }}1.5{M_{\rm{e}}}{\rm{ {\text{＋}} }}4.4{\text{，}}$
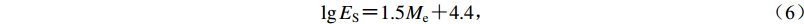
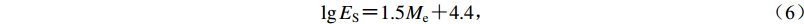
(6) 并在测定地震波能量的基础上，建立了能量震级Me的定义式：
${M_{\rm{e}}}{\rm{ {\text{＝}} }}\frac{2}{3}\left({{\rm{lg}}{E_{\rm{S}}}{\rm{ {\text{－}} }}4.4} \right){\text{.}}$
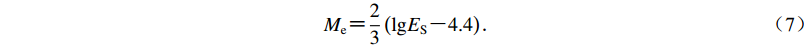
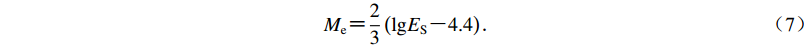
(7) 这样在使用式（5）计算地震波能量ES之后，使用式（7）即可快速得到能量震级Me的值。
2. 实际震例
本文根据上述方法自行设计了相关软件，下面将利用宽频带数字地震资料，测定M＞6.0地震的地震波能量ES和能量震级Me。
2.1 2017年8月8日MS7.0九寨沟地震
据我国地震台网测定，北京时间2017年8月8日21时19分，四川省阿坝州九寨沟县发生MS7.0地震，震中位于（103.82°E，33.20°N），震源深度为9 km。
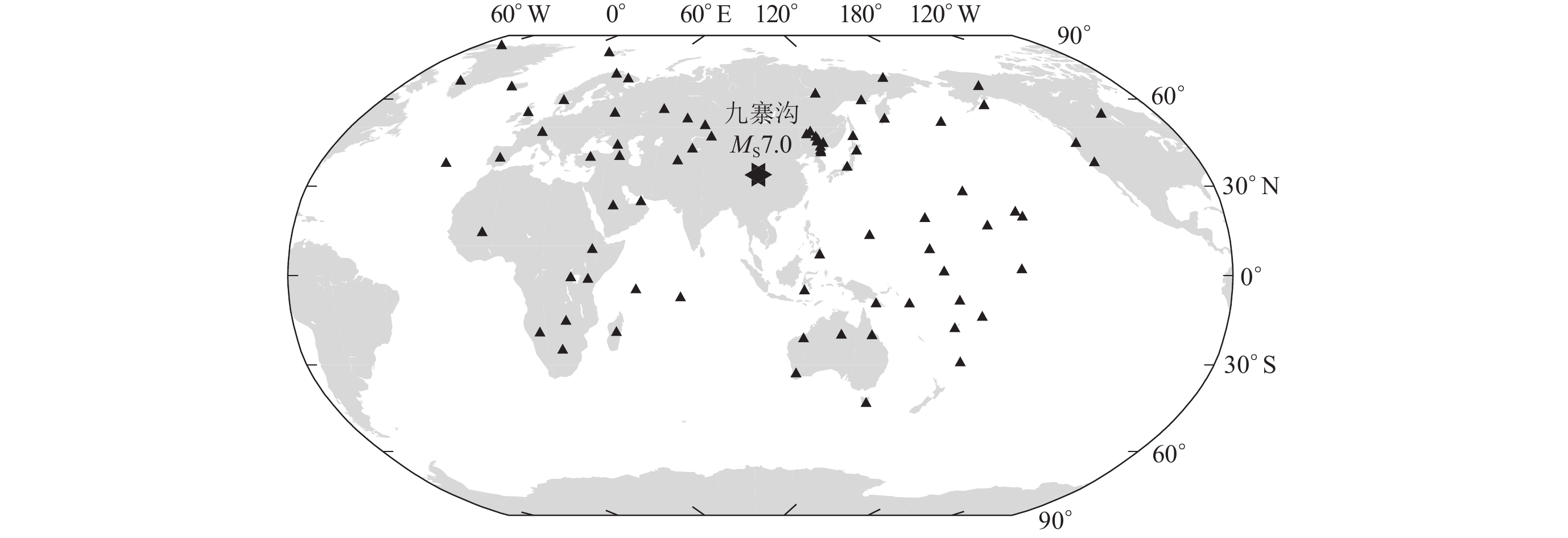
从IRIS网站上下载了全球地震台网（GSN）68个地震台站的宽频带波形数据，并使用国家地震台网10个地震台站的宽频带波形数据，地震台的震中距处于20°—98°范围内，图1为地震台站分布图。利用参考地球模型AK135Q （Kennett et al，1995）和QSSP软件包（Wang，1999）来计算球形地球的格林函数，用上述方法最终得到78个台站的能量震级详见表1，可见台站最大的能量震级为7.07，最小能量震级为5.89，平均能量震级Me为6.3，地震破裂持续时间为43 s。单台能量震级与平均能量震级之间的偏差见图2，可以看出单台能量震级与平均能量震级之间的偏差在−0.5—0.7之间。10个国家地震台站的能量震级在6.14—6.44之间，平均值为6.36。
![]()
图 1 计算九寨沟地震能量震级所用台站分布图Figure 1. Distribution of the stations used for calculation of energy magnitude of Jiuzhaigou earthquake表 1 计算九寨沟地震能量震级Me的单台数据Table 1. Single station data for calculating energy magnitude Me of Jiuzhaigou earthquake台站名 震中距/° Me 台站名 震中距/° Me 台站名 震中距/° Me IU.MAKZ 21.46 7.02 IU.MBWA 56.42 6.22 IU.PAB 81.55 6.18 BK.CMB 97.75 6.66 IU.WAKE 57.19 6.47 IU.FUNA 82.63 6.21 II.AAK 24.86 6.70 IU.KBS 57.87 6.24 IU.KIP 84.85 6.31 II.KURK 25.44 6.45 IU.ADK 58.32 6.46 II.TAU 85.86 6.34 IU.MAJO 28.23 6.36 IU.PMG 59.25 6.16 IU.LSZ 86.81 6.12 II.SIMI 28.57 6.50 II.MSEY 59.38 6.17 II.MSVF 87.12 6.66 II.BRVK 31.06 6.19 II.WRAB 60.58 6.06 IU.POHA 87.71 6.53 II.ERM 32.05 6.08 II.KWAJ 63.29 6.58 II.FFC 89.31 6.47 IU.YSS 32.37 6.12 IU.KONO 63.83 6.15 IU.COR 91.20 6.34 IU.DAV 32.98 6.76 II.ALE 64.10 6.08 IU.AFI 92.97 6.75 IU.YAK 33.20 6.30 IU.FURI 64.42 6.24 GT.LBTB 94.43 6.58 II.ARU 38.59 6.09 IU.MIDW 66.27 6.45 II.CMLA 94.85 6.48 IU.MA2 40.40 6.09 IU.CTAO 66.90 6.05 IU.XMAS 96.14 6.28 II.KAPI 41.07 6.31 IU.NWAO 67.31 6.56 IU.KOWA 96.41 6.95 IU.GUMO 42.06 6.53 IU.COLA 67.41 6.12 IU.RAO 96.80 6.22 II.UOSS 42.10 6.25 IU.HNR 68.24 6.57 IU.TSUM 97.39 7.07 IU.PET 43.32 5.89 II.KDAK 68.99 6.36 碾子山 20.30 6.63 IU.GNI 47.05 6.22 II.BFO 69.18 5.94 五常 21.50 6.55 II.KIV 47.89 6.29 IU.KMBO 71.25 5.92 讷河 21.77 6.01 IU.BILL 49.33 6.47 IU.TARA 71.83 6.85 宾县 21.97 6.35 II.DGAR 50.38 6.52 II.ESK 71.91 6.02 宝清 21.98 6.47 II.OBN 50.66 6.18 II.BORG 73.18 6.28 靖宇 21.06 6.14 II.RAYN 51.60 6.23 II.ABPO 75.12 6.18 柳河 20.95 6.21 II.LVZ 51.76 6.03 II.MBAR 76.27 6.63 丰满 21.55 6.42 IU.KEV 54.58 5.97 IU.SFJD 77.95 6.41 抚松 20.65 6.31 IU.ANTO 55.99 6.19 IU.JOHN 78.17 6.01 牡丹江 22.91 6.55 平均能量震级 6.3 注：表中10个中国台站的地震引自国家测震台网数据备份中心（2007）和郑秀芬等（2009）。 ![]()
图 2 九寨沟地震能量震级Me残差分布Figure 2. Distribution of the residuals for energy magnitude Me of the Jiuzhaigou earthquake从图2还可以看出，不同台站的能量震级的测定基本与台站位置无关，每个台站的能量震级稳定地集中于5.9—7.1之间。
2.2 2013年4月20日MS7.0芦山地震
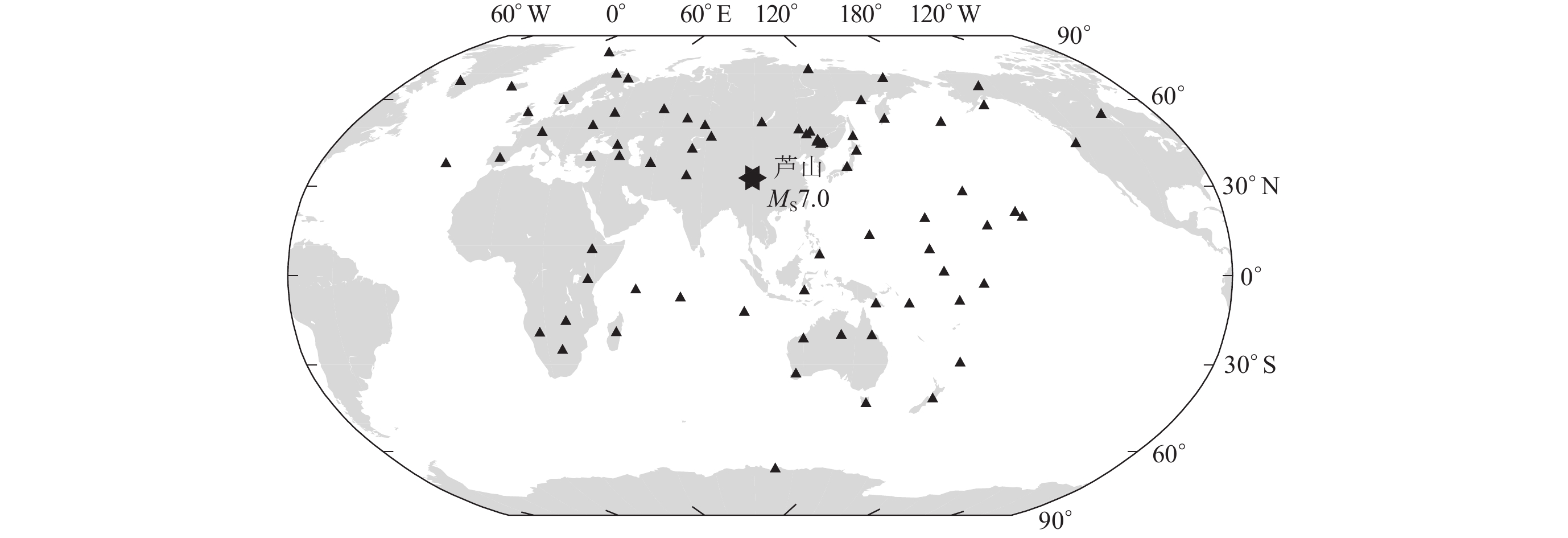
据我国地震台网测定，北京时间2013年4月20日8时2分四川省雅安市芦山县（30.3°N，103.0°E）发生MS7.0地震，震源深度为12.2 km。
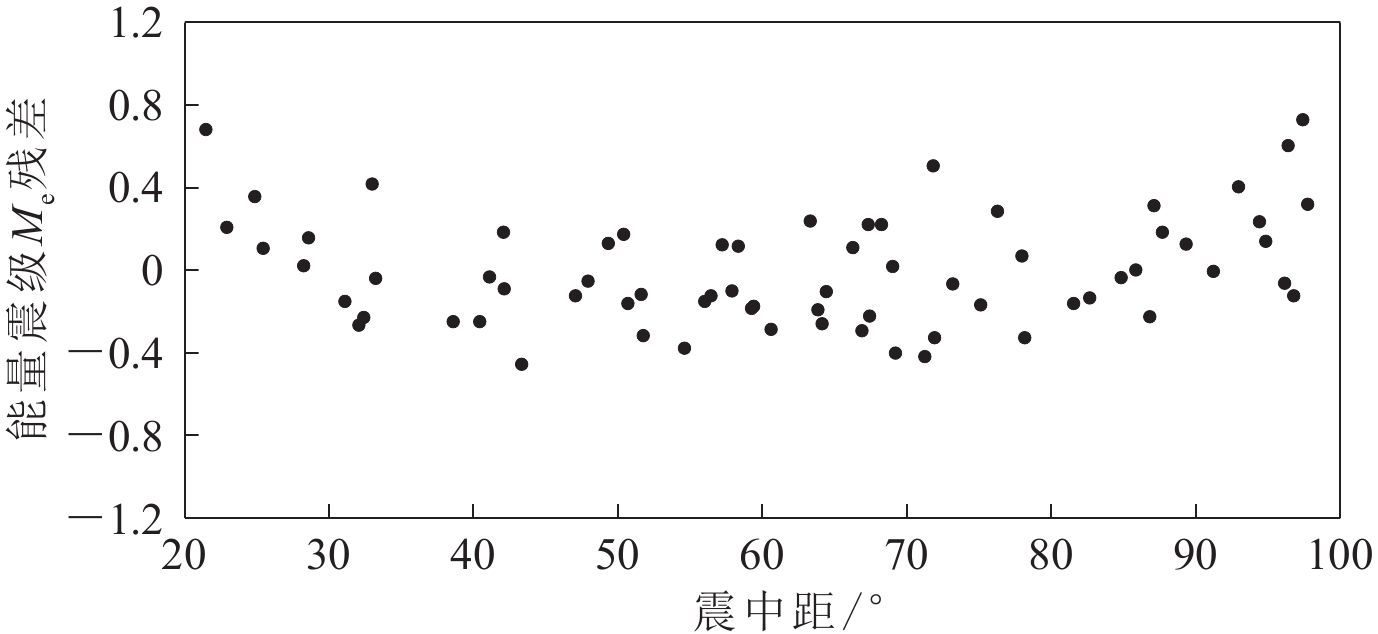
我们从IRIS网站上下载全球地震台网的68个地震台站记录到的芦山地震宽频带波形数据，并使用国家地震台网的5个地震台站的宽频带波形数据，地震台的震中距处于20°—98°范围内，图3为计算芦山地震能量震级所用地震台站的分布图。基于QSSP软件包计算格林函数，用上述方法得到73个台站的能量震级，台站最大的能量震级为7.25，最小能量震级为5.39，平均能量震级Me为6.61，地震破裂持续时间为39 s。基于5个国家地震台站数据获取的能量震级在6.08—7.04之间，平均值为6.64。单台能量震级与平均能量震级之间的偏差见图4，可以看出偏差处于−1.2—0.6之间。
![]()
图 3 计算芦山地震能量震级所用台站分布图Figure 3. Distribution of the stations used for calculation of energy magnitude of Lushan earthquake![]()
图 4 芦山地震能量震级Me残差分布Figure 4. Distribution of the residuals for energy magnitude Me of the Lushan earthquake2.3 其它震例
本文也测定了国外4次和国内4次中强震的能量震级Me，同时还收集了中国地震台网中心（China Earthquake Networks Center，简写为CENC）发布的这些地震的面波震级MS、美国哈佛大学和哥伦比亚大学拉蒙特-多赫蒂地球观象台全球矩心矩张量项目（GCMT）测定的矩震级MW以及美国地震学研究联合会（IRIS）发布的能量震级Me。表2为4次国内地震和4次国外地震的各项震级数据。
表 2 不同机构测定的4次国外和4次国内地震的各类震级Table 2. Various magnitudes measured by different institutes for four overseas and four domestic earthquakes发震时间 发震地点 震源深度
/km震源破裂
时间/s震源机制
类型MS
（CENC）MW
（GCMT）Me
（IRIS）Me
（本文）1991-04-22 哥斯达黎加 10.0 81 T 8.1 7.6 7.4 7.4 1992-09-02 尼加拉瓜 15.0 172 T 7.7 7.6 6.7 6.6 2006-11-15 昆士兰 39.0 133 T 8.0 8.3 7.7 7.7 2007-01-13 昆士兰 10.0 101 N 7.9 8.1 8.6 8.1 2008-05-12 四川汶川 12.8 126 TS 8.0 7.9 8.1 8.0 2013-04-20 四川芦山 12.2 39 T 7.0 6.6 6.7 6.6 2014-08-03 云南鲁甸 10.0 46 S 6.5 6.2 6.4 6.4 2017-08-08 四川九寨沟 9.0 43 S 7.0 6.5 6.4 6.3 注：T为逆断层，N为正断层，S为走滑断层，TS为包含走滑成分的逆断层。 3. 震例分析
3.1 芦山地震和九寨沟地震
2013年4月20日芦山地震与2017年8月8日九寨沟地震的震源仅相隔335 km，面波震级MS均为7.0，矩震级MW分别为6.6和6.5，基本相近，但实际上这两次地震的震感和所产生的破坏有显著区别。据李志强等（2013）统计，芦山地震造成196人死亡，21人失踪，13 884人受伤，而九寨沟地震造成25人死亡，525人受伤。中国地震局（2013，2017）通过灾区震害调查、强震动观测记录分析、遥感航空影像震害解译等确定了这两次地震的烈度分布：芦山地震的最高烈度为Ⅸ度，Ⅸ度烈度区的长半轴为11.5 km，短半轴为5.5 km，面积为208 km2，Ⅵ度及以上烈度区的总面积为18 682 km2；而九寨沟地震Ⅸ度烈度区涉及四川省九寨沟县漳扎镇，面积达139 km2，Ⅵ度及以上烈度区的总面积为14 006 km2。无论是Ⅸ度烈度区面积，还是Ⅵ度及以上烈度区的总面积，芦山地震都要比九寨沟地震的面积要大，Ⅸ度烈度区的面积比九寨沟地震大69 km2，Ⅵ度及以上烈度区的总面积比九寨沟地震大4 676 km2，所造成的地震灾害要严重。
从本文测定的能量震级Me来看，芦山地震的Me为6.6，九寨沟地震的Me为6.3，相差0.3；而从震源破裂时间来看，九寨沟地震的震源破裂时间为43 s，稍长于芦山地震的震源破裂时间39 s。这说明芦山地震所释放的能量要大于九寨沟地震，而芦山地震的震源破裂时间短，是造成芦山地震灾害比较严重的因素之一。
地震波能量ES反映震源动态特征，与地震震源的动力学特性（如地震波频率、地震波速度等）密切相关。地震以地震波形式辐射的能量主要集中在震源谱的拐角频率附近，因此能量震级Me更适合描述地震的潜在破坏性。对于地震灾害与风险评估，人们更关注的是地震辐射能量ES的大小，特别是其高频成分的地震辐射能量。
3.2 芦山地震和鲁甸地震
2014年8月3日云南鲁甸MS6.5地震灾区的最高烈度为Ⅸ度，等震线长轴总体呈北北西走向，Ⅵ度及以上烈度区的总面积为10 350 km2，造成云南省、四川省、贵州省共10个县（区）受灾。截至2014年8月8日15时，该地震共造成617人死亡、112人失踪、3 143人受伤、22.97万人紧急转移安置。鲁甸地震产生了令人意想不到的破坏力，造成了巨大的经济损失和人员伤亡。地球物理学家们从地质构造、建筑物抗震性能及人口密度等方面均进行了分析，然而却无法解释鲁甸MS6.5地震的震中烈度已经与MS7.0的芦山地震一样达到了Ⅸ度。接下来本文将从地震波能量释放的角度上对比芦山地震与鲁甸地震。
Convers和Newman （2011）对全球大地震的地震波能量与震源机制关系进行了统计分析，结果表明，对于走滑型、正断层型和逆冲型震源机制，其地震波能量与地震矩的比值分别为3.63×10−5，3.09×10−5，1.82×10−5。走滑型地震更容易促进地震能量释放，正断层型次之，逆冲型地震的能量释放效果更差。由表2可知，云南鲁甸地震是走滑型地震，芦山地震是逆冲型地震，两次地震的面波震级相差0.5，矩震级相差0.4，由于走滑型地震的能量释放能力远超逆冲型地震，因此本文计算所得的两次地震的能量震级仅相差0.2。从面波震级和矩震级可以推算两次地震的地震波能量应该相差4—5.6倍，然而从两次地震的实际受灾情况分析可知，两次地震的破坏力相差并没有那么大。从能量震级的角度分析，芦山地震的地震波能量大致为鲁甸地震的两倍，这样的结果更加符合实际情况。总之，在地震监测的过程中，发震之后尽快估算出地震的能量震级和地震波能量，进而快速地确定应急响应级别并采取相应的救灾措施（赵仲和，2014）。
3.3 哥斯达黎加地震和尼加拉瓜地震
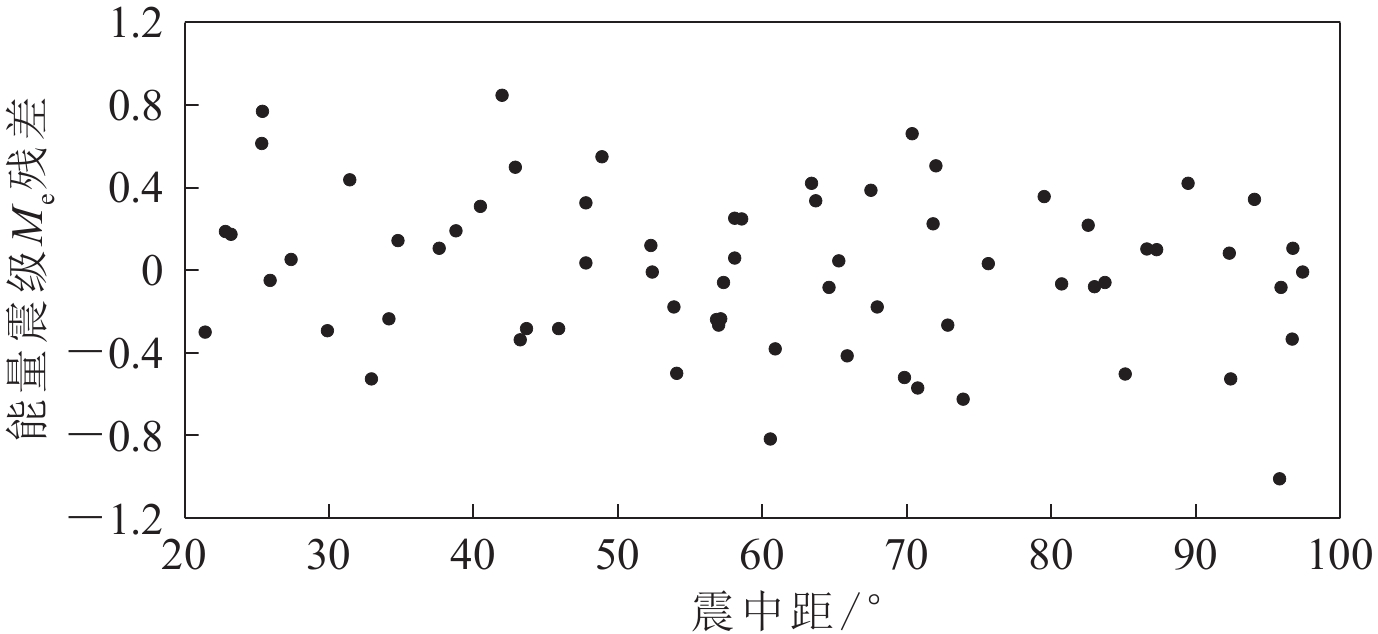
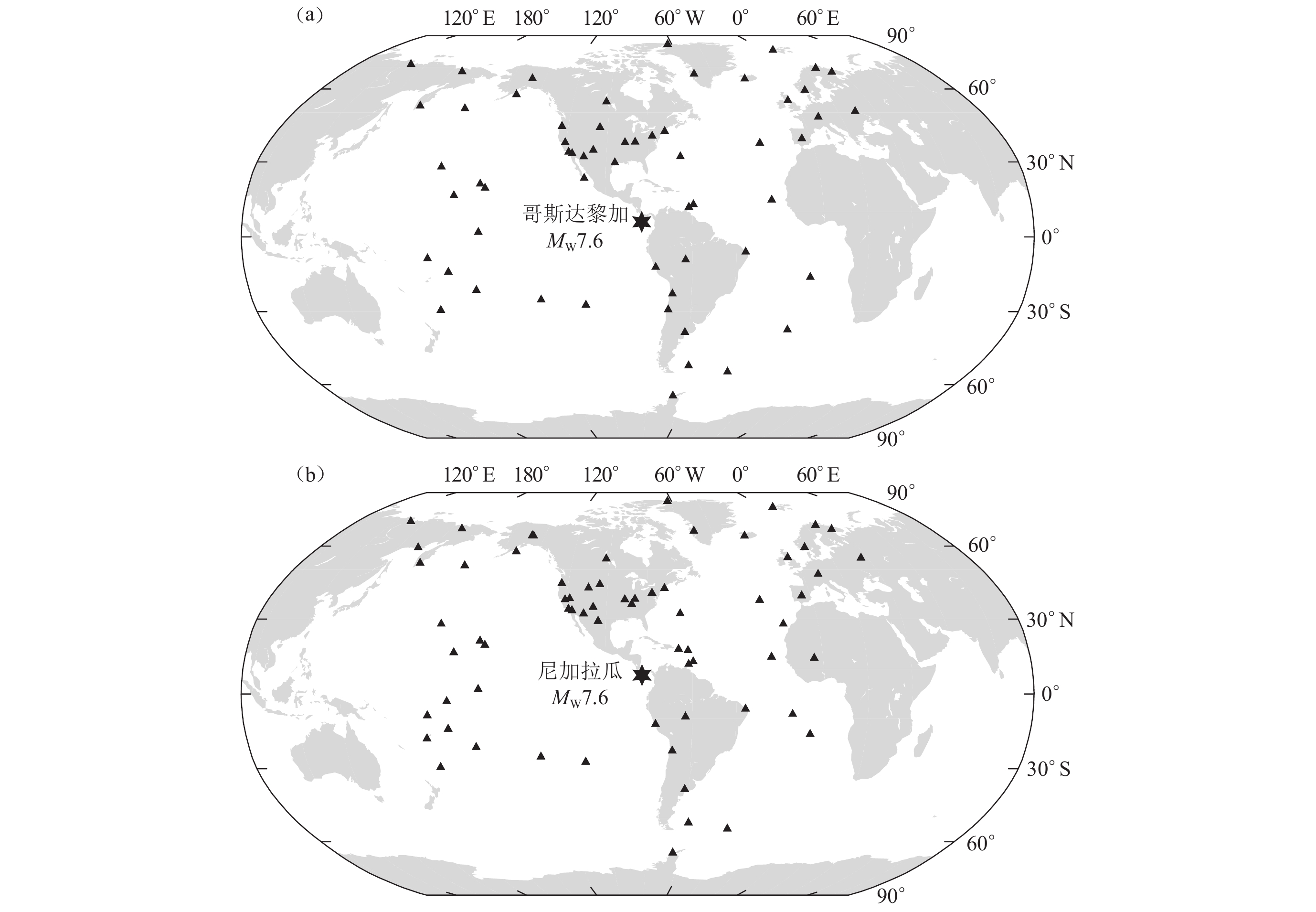
1991—1992年美洲中部发生两次地震，一次是1991年4月22日的哥斯达黎加（Costa Rica）地震，另一次是1992年9月2日尼加拉瓜（Nicaragua）地震，这两次地震相距大约500 km，图5为测定这两次地震能量震级所用台站的分布图。NEIC （1991，1992）测定的这两次地震的震源机制均为逆断层，矩震级MW均为7.6，即具有相同的地震矩M0。对于远场而言，可以认为两次地震的震中位置比较接近，地震波的传播路径也比较接近。
![]()
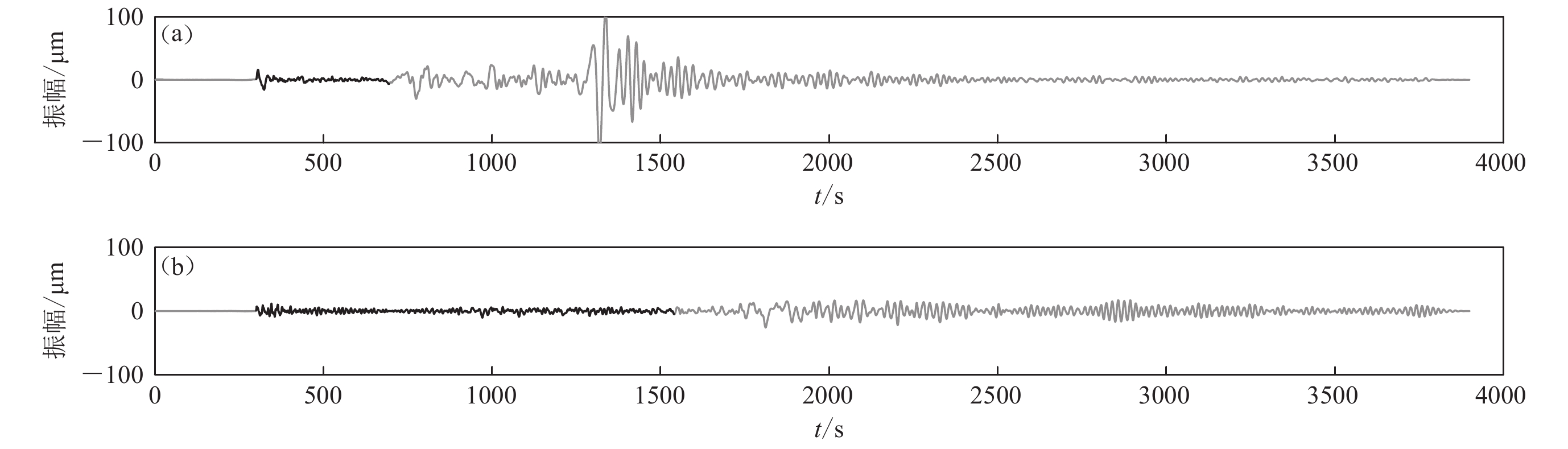
图 5 计算哥斯达黎加地震（a）和尼加拉瓜地震（b）能量震级所用台站分布图Figure 5. Distribution of the stations used for calculation of energy magnitude of Costa Rica earthquake （a） and Nicaragua earthquake （b）从本文的测定结果来看：哥斯达黎加地震的能量震级Me为7.4，震源破裂时间为81 s；尼加拉瓜地震的能量震级Me为6.6，震源破裂时间为172 s。前者的地震辐射能量ES明显大于后者，前者的震源破裂时间明显小于后者，这说明前者的辐射能量较大，震源破裂速度很快，而后者的辐射能量较小，震源破裂速度很慢。此外，本文还截取了我国牡丹江地震台记录到的这两次地震的波形记录，如图6所示，其中上图为哥斯达黎加地震波形（震中距为118.45°，方位角为334.0°），下图为尼加拉瓜地震（震中距为114.68°，方位角为331.0°），两图的比例完全一样。通过对比可以得知，虽然这两次地震的位置相距并不远，但牡丹江地震台记录到的这两次地震的波形特征却有明显的差别：哥斯达黎加地震的P波和面波幅值较大，地震波衰减得却很快（图6a），而尼加拉瓜地震的P波和面波幅值较小，地震波衰减得却很慢（图6b）。
![]()
图 6 牡丹江地震台记录到的哥斯达黎加地震（a）和尼加拉瓜地震（b）的波形记录图Figure 6. Comparison of P-waveforms from Costa Rica earthquake （a） and Nicaragua earthquake （b） recorded by the station MDJ从这两次地震造成的灾害来看，尼加拉瓜地震产生了海啸，海浪高达8 m，而哥斯达黎加地震则产生了非常强烈的地面震动，震中烈度达到Ⅹ度，产生了严重的破坏。这说明单独依靠地震矩M0 （或矩震级MW）并不能准确地反映地震的潜在破坏程度。Di Giacomo （2010）使用Bormann和Saul （2008）的方法对比了两次地震的S−P时窗和高频包络线，并对包含破裂持续时间的时窗的S变换进行了时频分析（Stockwell et al，1996；Parolai，2009），其时频分析结果表明，哥斯达黎加地震的地震能量主要分布于两个不同的能量脉冲，分别在0.1 Hz处和0.04—0.05 Hz左右达到峰值，二者之间相隔几秒钟。这两个脉冲可能与所确定的两个主要破裂有关（Goes et al，1993），然而，根据S变换图，能量释放集中的频段主要分布于高于0.1 Hz的频率。因此，哥斯达黎加地震的例子说明了时频分析在量化有关震源破裂过程的重要细节方面的实用性，单从时域分析不那么明显。尼加拉瓜地震是缓慢地震引发大海啸的最佳震例之一（例如，Kanamori，Kikuchi，1993），与哥斯达黎加地震相比该地震的高频成分明显减少，能量主要分布于0.1 Hz以下，并在更长的破裂时间内扩散。但是，两次地震的低频S变换振幅相差无几，这是我们通过其相近的矩震级很容易预想到的。两次地震不同的高频成分导致了能量震级的差异。
对于地震灾害与风险评估，更令人关注的是地震辐射能量ES的大小，特别是其高频成分的地震辐射能量。从断裂动力学和运动学以及地震所造成的破坏的角度来说，ES与应力降和震源破裂速度密切相关，因此，联合测定MW和ES对于量化和评估地震或海啸造成的灾害评估十分有效（Choy，Boatwright，2007）。
与尼加拉瓜地震和哥斯达黎加地震类似的，还有2006年11月15日和2007年1月13日的昆士兰地震。这两次大地震的发震时间、地点均很近，时间相差59天，震中仅相距102 km，地震矩也相差无几，短周期体波振幅却呈显著差异（Ammon et al，2008）。2006年、2007年昆士兰地震的MW分别为8.3和8.1，相差不大。在能量震级测定方面，本文测定的结果为7.66和8.10，这表明2007年昆士兰地震的能量释放要明显高于2006年的。根据NEIC （2006，2007）对这两次地震的震感报告，2006年昆士兰地震只有俄罗斯和日本的少部分地区有轻微震感，而2007年地震的烈度在俄罗斯的部分地区甚至达到了Ⅵ；另一方面2006年地震引发了176 cm高的大海啸，而2007年地震仅引发轻微海啸。GFZ的能量震级结果为7.76和8.57 （Di Giacomo，2010），USGS的结果为7.73和8.15。
4. 讨论与结论
本文使用了全球地震台网和国家地震台网的宽频带地震数据，利用汪荣江教授的QSSP软件包计算格林函数，开展了地震波能量ES和能量震级Me的测定方法研究。利用震中距在20°—98°范围内的宽频带远震P波波形数据，测定了4次国外和4次国内中强震的能量震级Me，并将该结果与中国地震台网中心测定的面波震级MS、GCMT测定的矩震级MW进行了分析对比，主要结论如下：
1） 本文对2013年4月20日芦山地震、2014年8月3日云南鲁甸地震与2017年8月8日九寨沟地震这三个震例进行了相互对比，结果表明：地震造成的地震灾害直接与地震释放的地震波能量ES相关。地震灾害是地震波对传播路径区域造成的破坏，因此地震波能量是一个至关重要的参数。
地震波能量的测定对海啸的预警也有实际意义，通过1991年4月22日哥斯达黎加地震与1992年9月2日尼加拉瓜地震的对比，我们可以得到结论：对于相同地震矩的逆冲断层型地震，能量震级越大，破裂持续时间越短，震感越强烈；反之，能量震级越小，破裂持续时间越长，易引发海啸。
因此，地震发生后，尽快测定地震波能量ES和能量震级Me，对于及时量化和评估地震灾害、确定大地震应急响应级别以及采取相应救灾措施具有重要意义。
2） 本文测定地震波能量目前有两大局限：一是受仪器和地球模型的限制，只能得到大约1—70 s范围内的宽频带结果而不是全频段结果；二是由于使用的是远震数据，因此只能测定M＞5.0地震，对于小地震，由于波形信噪比的问题，无法给出准确的测量结果。
3） 目前全世界只有IRIS可以日常产出地震波能量ES和能量震级Me，本文根据文献中的理论知识，自行设计了测定能量震级的程序，并对震例的各项参数进行了对比。此外，本文在测定能量震级的过程中首次使用了中国台站的数据。
今后需要在以下两方面展开研究：一是大批量地测定能量震级，丰富震例，进行更深层次的研究，例如，海啸地震的特征和震源机制对地震能量释放的影响等；二是对程序进一步自动化，以期能够像IRIS一样日常产出地震波能量ES和能量震级Me。
全球地震台网（GSN）与国家地震台网提供了宽频带波形数据，德国地球科学中心的汪荣江教授提供了QSSP软件包，作者在此一并表示诚挚的感谢。
-
![]()
图 1 计算九寨沟地震能量震级所用台站分布图
Figure 1. Distribution of the stations used for calculation of energy magnitude of Jiuzhaigou earthquake
![]()
图 2 九寨沟地震能量震级Me残差分布
Figure 2. Distribution of the residuals for energy magnitude Me of the Jiuzhaigou earthquake
![]()
图 3 计算芦山地震能量震级所用台站分布图
Figure 3. Distribution of the stations used for calculation of energy magnitude of Lushan earthquake
![]()
图 4 芦山地震能量震级Me残差分布
Figure 4. Distribution of the residuals for energy magnitude Me of the Lushan earthquake
![]()
图 5 计算哥斯达黎加地震（a）和尼加拉瓜地震（b）能量震级所用台站分布图
Figure 5. Distribution of the stations used for calculation of energy magnitude of Costa Rica earthquake （a） and Nicaragua earthquake （b）
![]()
图 6 牡丹江地震台记录到的哥斯达黎加地震（a）和尼加拉瓜地震（b）的波形记录图
Figure 6. Comparison of P-waveforms from Costa Rica earthquake （a） and Nicaragua earthquake （b） recorded by the station MDJ
表 1 计算九寨沟地震能量震级Me的单台数据
Table 1 Single station data for calculating energy magnitude Me of Jiuzhaigou earthquake
台站名 震中距/° Me 台站名 震中距/° Me 台站名 震中距/° Me IU.MAKZ 21.46 7.02 IU.MBWA 56.42 6.22 IU.PAB 81.55 6.18 BK.CMB 97.75 6.66 IU.WAKE 57.19 6.47 IU.FUNA 82.63 6.21 II.AAK 24.86 6.70 IU.KBS 57.87 6.24 IU.KIP 84.85 6.31 II.KURK 25.44 6.45 IU.ADK 58.32 6.46 II.TAU 85.86 6.34 IU.MAJO 28.23 6.36 IU.PMG 59.25 6.16 IU.LSZ 86.81 6.12 II.SIMI 28.57 6.50 II.MSEY 59.38 6.17 II.MSVF 87.12 6.66 II.BRVK 31.06 6.19 II.WRAB 60.58 6.06 IU.POHA 87.71 6.53 II.ERM 32.05 6.08 II.KWAJ 63.29 6.58 II.FFC 89.31 6.47 IU.YSS 32.37 6.12 IU.KONO 63.83 6.15 IU.COR 91.20 6.34 IU.DAV 32.98 6.76 II.ALE 64.10 6.08 IU.AFI 92.97 6.75 IU.YAK 33.20 6.30 IU.FURI 64.42 6.24 GT.LBTB 94.43 6.58 II.ARU 38.59 6.09 IU.MIDW 66.27 6.45 II.CMLA 94.85 6.48 IU.MA2 40.40 6.09 IU.CTAO 66.90 6.05 IU.XMAS 96.14 6.28 II.KAPI 41.07 6.31 IU.NWAO 67.31 6.56 IU.KOWA 96.41 6.95 IU.GUMO 42.06 6.53 IU.COLA 67.41 6.12 IU.RAO 96.80 6.22 II.UOSS 42.10 6.25 IU.HNR 68.24 6.57 IU.TSUM 97.39 7.07 IU.PET 43.32 5.89 II.KDAK 68.99 6.36 碾子山 20.30 6.63 IU.GNI 47.05 6.22 II.BFO 69.18 5.94 五常 21.50 6.55 II.KIV 47.89 6.29 IU.KMBO 71.25 5.92 讷河 21.77 6.01 IU.BILL 49.33 6.47 IU.TARA 71.83 6.85 宾县 21.97 6.35 II.DGAR 50.38 6.52 II.ESK 71.91 6.02 宝清 21.98 6.47 II.OBN 50.66 6.18 II.BORG 73.18 6.28 靖宇 21.06 6.14 II.RAYN 51.60 6.23 II.ABPO 75.12 6.18 柳河 20.95 6.21 II.LVZ 51.76 6.03 II.MBAR 76.27 6.63 丰满 21.55 6.42 IU.KEV 54.58 5.97 IU.SFJD 77.95 6.41 抚松 20.65 6.31 IU.ANTO 55.99 6.19 IU.JOHN 78.17 6.01 牡丹江 22.91 6.55 平均能量震级 6.3 注：表中10个中国台站的地震引自国家测震台网数据备份中心（2007）和郑秀芬等（2009）。 
下载: 导出CSV
表 2 不同机构测定的4次国外和4次国内地震的各类震级
Table 2 Various magnitudes measured by different institutes for four overseas and four domestic earthquakes
发震时间 发震地点 震源深度
/km震源破裂
时间/s震源机制
类型MS
（CENC）MW
（GCMT）Me
（IRIS）Me
（本文）1991-04-22 哥斯达黎加 10.0 81 T 8.1 7.6 7.4 7.4 1992-09-02 尼加拉瓜 15.0 172 T 7.7 7.6 6.7 6.6 2006-11-15 昆士兰 39.0 133 T 8.0 8.3 7.7 7.7 2007-01-13 昆士兰 10.0 101 N 7.9 8.1 8.6 8.1 2008-05-12 四川汶川 12.8 126 TS 8.0 7.9 8.1 8.0 2013-04-20 四川芦山 12.2 39 T 7.0 6.6 6.7 6.6 2014-08-03 云南鲁甸 10.0 46 S 6.5 6.2 6.4 6.4 2017-08-08 四川九寨沟 9.0 43 S 7.0 6.5 6.4 6.3 注：T为逆断层，N为正断层，S为走滑断层，TS为包含走滑成分的逆断层。
下载: 导出CSV
-
陈培善. 1990. 地震定量的国际现状[J]. 地震地磁观测与研究, 11（3）: 33-39. Chen P S. 1990. The international status of earthquake quantification[J]. Seismological and Geomagnetic Observation and Research, 11（3）: 33-39 （in Chinese）.
国家测震台网数据备份中心. 2007. 国家测震台网地震波形数据[DB/OL]. 中国地震局地球物理研究所. http://www. seisdmc.ac.cn. doi: 10.11998/SeisDmc/SN. Data Management Centre of China National Seismic Network. 2007. Waveform data of China national seismic network[DB/OL]. Institute of Geophysics, China Earthquake Administration. http://www.seisdmc.ac.cn. doi: 10.11998/SeisDmc/SN （in Chinese）.
李志强, 侯建盛, 李洋, 苏桂武, 姜立新, 孙柏涛, 袁一凡, 林均岐. 2013. 2013年4月20日四川芦山MS7.0地震灾害特点分析[J]. 地震地质, 35（2）: 398-410. doi: 10.3969/j.issn.0253-4967.2013.02.018 Li Z Q, Hou J S, Li Y, Su G W, Jiang L X, Sun B T, Yuan Y F, Lin J Q. 2013. Analysis on the Characteristics of the MS7.0 Lushan, Sichuan province, earthquake hazard on April 20, 2013[J]. Seismology and Geology, 35（2）: 398-410 （in Chinese）.
赵仲和. 2014. 2014年8月3日云南鲁甸M6.5地震的地震波能量[J]. 国际地震动态, （9）: 24-28, 34. doi: 10.3969/j.issn.0235-4975.2014.09.007 Zhao Z H. 2014. Seismic energy of Ludian M6.5 earthquake, August 3, 2014[J]. Recent Developments in World Seismology, （9）: 24-28, 34 （in Chinese）.
郑秀芬, 欧阳飚, 张东宁, 姚志祥, 梁建宏, 郑洁．2009. " 国家测震台网数据备份中心”技术系统建设及其对汶川大地震研究的数据支撑[J]．地球物理学报, 52（5）: 1412—1417． doi: 10.3969/j.issn.0001-5733.2009.05.031 Zheng X F, Ouyang B, Zhang D N, Yao Z X, Liang J H, Zheng J. 2009. Technical system construction of Data Backup Centre for China Seismograph Network and the data support to researches on the Wenchuan earthquake. Chinese Journal of Geophysics, 52（5）:1412—1417（in Chinese）.
中国地震局. 2013. 中国地震局发布四川省芦山" 4·20”7.0级强烈地震烈度图[EB/OL]. [2018−11−15]. https://www.cea.gov.cn/cea/xwzx/fzjzyw/5195229/index.html. China Earthquake Administration. 2013. China Earthquake Administration release the seismic intensity map of Lushan Sichuan M7.0 strong earthquake on April 20, 2017[EB/OL]. [2018-11-15]. https://www.cea.gov.cn/cea/xwzx/fzjzyw/5195229/index.html （in Chinese）.
中国地震局. 2017. 中国地震局发布四川九寨沟7.0级地震烈度图[EB/OL]. [2018−11−15]. https://www.cea.gov.cn/cea/xwzx/fzjzyw/5206273/index.html. China Earthquake Administration. 2017. China Earthquake Administration release the seismic intensity map of Jiuzhaigou Sichuan M7.0 earthquake[EB/OL]. [2018-11-15]. https://www.cea.gov.cn/cea/xwzx/fzjzyw/5206273/index.html （in Chinese）.
Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods[M]. San Francisco: W. H. Freeman: 932.
Ammon C J, Kanamori H, Lay T. 2008. A great earthquake doublet and seismic stress transfer cycle in the central Kuril islands[J]. Nature, 451（7178）: 561-565. doi: 10.1038/nature06521
Boatwright J, Choy G L. 1986. Teleseismic estimates of the energy radiated by shallow earthquakes[J]. J Geophys Res, 91（B2）: 2095-2112. doi: 10.1029/JB091iB02p02095
Bormann P, Liu R F, Ren X, Gutdeutsch R, Kaiser D, Castellaro S. 2007. Chinese National Network magnitudes, their relation to NEIC Magnitudes, and recommendations for new IASPEI magnitude standards[J]. Bull Seismol Soc Am, 97（1B）: 114-127. doi: 10.1785/0120060078
Bormann P, Saul J. 2008. The new IASPEI standard broadband magnitude mB[J]. Seismol Res Lett, 79（5）: 698-705. doi: 10.1785/gssrl.79.5.698
Bormann P, Saul J. 2009a. Earthquake magnitude[G]//Encyclopedia of Complexity and Systems Science. Heidelberg: Springer: 2473−2496.
Bormann P, Saul J. 2009b. A fast, non-saturating magnitude estimator for great earthquakes[J]. Seism Res Lett, 80（5）: 808-816. doi: 10.1785/gssrl.80.5.808
Choy G L, Boatwright J L. 1995. Global patterns of radiated seismic energy and apparent stress[J]. J Geophys Res, 100（B9）: 18205-18228. doi: 10.1029/95JB01969
Choy G L, Boatwright J. 2007. The energy radiated by the 26 December 2004 Sumatra-Andaman earthquake estimated from 10-minute P-wave windows[J]. Bull Seismol Soc Am, 97（1A）: S18-S24. doi: 10.1785/0120050623
Convers J A, Newman A V. 2011. Global evaluation of large earthquake energy from 1997 through mid-2010[J]. J Geophys Res, 116（B8）: B08304.
Di Bona M, Rovelli A. 1988. Effects of bandwidth limitation on stress drop estimated from integrals of the ground motion[J]. Bull Seismol Soc Am, 78: 1818-1825.
Di Giacomo D, Grosser H, Parolai S, Bormann P, Wang R J. 2008. Rapid determination of Me for strong to great shallow earthquakes[J]. Geophys Res Lett, 35（10）: L10308.
Di Giacomo D. 2010. Determination of the Energy Magnitude ME: Application to Rapid Response Purposes and Insights to Regional/Local Variabilities[D]. Potsdam: Universität Potsdam: 49−57.
Duda S J, Yanovskaya T B. 1993. Spectral amplitude-distance curves for P-waves: effects of velocity and Q-distribution[J]. Tectonophysics, 217（3/4）: 255-265.
Goes S D B, Velasco A A, Schwartz S Y, Lay T. 1993. The April 22, 1991, Valle de la Estrella, Costa Rica （MW=7.7） earthquake and its tectonic implications: A broadband seismic study[J]. J Geophys Res, 98（B5）: 8127-8142. doi: 10.1029/93JB00019
Gutenberg B, Richter C F. 1954. Seismicity of the Earth and Associated Phenomena[M]. 2nd ed. Princeton: Princeton University Press: 1−15.
Haskell N A. 1964. Total energy spectra density of elastic waves for propagating faults[J]. Bull Seismol Soc Am, 54（6）: 1811-1841.
Ide S, Beroza G C. 2001. Does apparent stress vary with earthquake size?[J]. Geophys Res Lett, 28（17）: 3349-3352. doi: 10.1029/2001GL013106
Kanamori H, Mori J, Hauksson E, Heaton T H, Hutton L K, Jones L M. 1993. Determination of earthquake energy-release and ML using TERRAscope[J]. Bull Seismol Soc Am, 83（2）: 330-346.
Kanamori H, Kikuchi M. 1993. The 1992 Nicaragua earthquake: a slow tsunami earthquake associated with subducted sediments[J]. Nature, 361（6414）: 714-716. doi: 10.1038/361714a0
Kennett B L N, Engdahl E R, Buland R. 1995. Constraints on seismic velocities in the Earth from traveltimes[J]. Geophys J Int, 122（1）: 108-124. doi: 10.1111/gji.1995.122.issue-1
Lomax A, Michelini A, Piatanesi A. 2007. An energy-duration procedure for rapid determination of earthquake magnitude and tsunamigenic potential[J]. Geophys J Int, 170（3）: 1195-1209. doi: 10.1111/gji.2007.170.issue-3
Montagner J P, Kennett B L N. 1996. How to reconcile body-wave and normal-mode reference Earth models[J]. Geophys J Int, 125（1）: 229-248. doi: 10.1111/gji.1996.125.issue-1
NEIC. 1991. Today in earthquake history[EB/OL]. [2018−11−15]. https://earthquake.usgs.gov/learn/today/index.php? month=4&day=22.
NEIC. 1992. M7.7−near the coast of Nicaragua[EB/OL]. [2018−11−15]. https://earthquake.usgs.gov/earthquakes/eventpage/ usp0005ddn/executive.
NEIC. 2006. M8.3−Kuril Islands[EB/OL]. [2018−11−15]. https://earthquake.usgs.gov/earthquakes/eventpage/usp000exfn/executive.
NEIC. 2007. M8.1−east of the Kuril Islands[EB/OL]. [2018−11−15]. https://earthquake.usgs.gov/earthquakes/eventpage/ usp000f2ab/executive.
Newman A V, Okal E A. 1998. Teleseismic estimates of radiated seismic energy: the E/M0 discriminant for tsunami earthquakes[J]. J Geophys Res, 103（B11）: 26885-26898. doi: 10.1029/98JB02236
Parolai S. 2009. Denoising of seismograms using the S transform[J]. Bull Seismol Soc Am, 99（1）: 226-234. doi: 10.1785/0120080001
Richter C F. 1935. An instrumental earthquake magnitude scale[J]. Bull Seismol Soc Am, 25（1）: 1-32.
Rudnicki J W, Freund L B. 1981. On energy radiation from seismic sources[J]. Bull Seismol Soc Am, 71（3）: 583-595.
Singh S K, Ordaz M. 1994. Seismic energy release in Mexican subduction zone earthquakes[J]. Bull Seismol Soc Am, 84（5）: 1533-1550.
Stockwell R G, Mansinha L, Lowe R P. 1996. Localization of the complex spectrum: the S transform[J]. IEEE Trans Signal Process, 44（4）: 998-1001. doi: 10.1109/78.492555
Venkataraman A, Kanamori H. 2004a. Effect of directivity on estimates of radiated seismic energy[J]. J Geophys Res, 109（B4）: B04301.
Wang R J. 1999. A simple orthonormalization method for stable and efficient computation of Green’s functions[J]. Bull Seismol Soc Am, 89（3）: 733-741.
-
期刊类型引用(10)
1. 王桂林，刘芳，王韬，翟浩，舒雷，贾彦杰，韩晓雷，周煊超，魏建民，郭伟，苏日亚，赵艳红，张茜，尚立坚，贾昕晔，吴卫远，戴怡茹. 内蒙古黑岱沟露天煤矿抛掷爆破地方性震级与炸药量的经验关系. 地震研究. 2025(01): 170-176 . 
百度学术
2. 谢紫藤，刘瑞丰，王子博，李赞，孔韩东，胡岩松. 震源机制对地震辐射能量估计的影响. 地震学报. 2023(04): 597-608 . 本站查看
3. 孔韩东，刘瑞丰，边银菊，李赞，王子博，胡岩松. 地震辐射能量测定方法研究及其在汶川8.0级地震中的应用. 地球物理学报. 2022(12): 4775-4788 . 百度学术
4. 冯增朝，吕兆兴，赵阳升. 岩石破坏短临预报研究进展——岩石破坏短临预报竞赛评述. 岩石力学与工程学报. 2022(12): 2522-2529 . 百度学术
5. 詹小艳，章东，王凯，王俊. 江苏数字地震台网P波谱震级和地震辐射能的计算. 地震研究. 2021(01): 15-21 . 百度学术
6. 王子博，刘瑞丰，孙丽，李赞，孔韩东. 2021年云南漾濞M_S6.4地震辐射能量的快速测定. 地震地质. 2021(04): 908-919 . 百度学术
7. 卢强，丁洋，刘赟哲，唐仕英，郭志昀，王占江. 黏弹性固体中地下爆炸辐射地震波能量的演化. 爆炸与冲击. 2021(09): 54-62 . 百度学术
8. 宋金，陈运泰，张勇. 2013年岷漳地震和2014年景谷地震的能矩比对比研究. 地球物理学报. 2020(09): 3324-3337 . 百度学术
9. 王婷，延军平，李双双，万佳，张玉凤. 帕米尔高原Mw≥6.6级地震时间韵律特征. 高原地震. 2020(04): 6-16 . 百度学术
10. 刘瑞丰，李赞，张玲，刘晓锋，王俊，李恩来，刘芳. 爆炸当量估算的初步研究. 地震地磁观测与研究. 2019(04): 1-7 . 百度学术
其他类型引用(5)
计量
- 文章访问数: 1721
- HTML全文浏览量: 1064
- PDF下载量: 100
- 被引次数: 15
