Weighted two-step regression method of attenuation relationship considering sample uneven distribution
-
摘要: 通过对距离和震级的分档将权重引入两步回归法: 第一步， 将地震记录按距离分档， 每个记录得到的权重为w'ij=1/(njni)(其中nj为该记录所在档的地震数， ni为该记录的地震在此档中的记录数)， 这种权重的取法不仅使各档的权重相同， 而且保证每档中不同地震在各档中的权重也相同； 第二步， 将地震按震级分档， 每次地震得到的权重为v'k=1/nk(其中nk为该地震所在档的地震数). 以Joyner 和Boore的数据为分析对象进行加权两步法的回归， 并与传统两步法回归的结果进行比较. 结果表明: 传统两步法在近场拟合的小震峰值加速度的估计值偏大， 大震峰值加速度的估计值偏小， 其衰减曲线在远场的衰减速度过快； 而加权两步法则能更好地反映地震动的空间分布规律.Abstract: Weight is introduced into two-step method by grading distances and magnitude. In the first step, the recordings are divided into several intervals by range of distances. Every recording gets one weight w'ij=1/(njni) (nj is the number of earthquakes in the interval in which the recording is located, ni is the number of recordings of the earthquake in this interval). Not only does the way of getting weight keep equal weight for every interval, but also promises the same weight for earthquakes in any interval. In the second step, the earthquakes are divided into several intervals by range of magnitudes. Every earthquake get one weight v'k=1/nk (nk is the number of earthquakes in the interval in which the earthquake is located). Taking the recordings used by Joyner and Boore (1981) as instance, comparing results from weighted two-step method with that from traditional one, the results show that values of peak ground acceleration (PGA) in near sites fitted by traditional method are higher than that fitted by weighted method for small events and lower for large events, attenuating rates are much rapider in far sites; weighted two-step method is better to simulate spatial distribution laws of ground motions than traditional method.
-
Keywords:
- weight /
- two-step method /
- peak ground acceleration /
- distribution law
-
引言
地震动衰减关系研究是与地震危险性分析和地震动区划工作相关的一个重要环节，其合理与否直接关系着地震危险性分析和地震动区划的合理性． 地震动衰减关系主要是反映地震动随震级、 距离等变化的关系式． 其一般形式为
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
早期的衰减关系都是直接利用最小二乘法对式(1)进行回归拟合，从而得到参数的估计值． Joyner和Boore(1981)提出了一种衰减关系的两步回归法． 第一步，使
式中： i为地震编号； N为地震总数； Ei为一虚拟变量(对于第i次地震Ei取1，其它地震取0)； Mi表示第i次地震的震级； Ai，a，b为回归参数. 将式(2)带入式(1)，利用记录数据中的距离和地震动两个参数拟合出Ai，c，d，R0的估计值. 第二步，结合第一步的Ai估计值和震级两个参数，利用式(2)拟合出a，b的估计值. 两步法在很大程度上减少了由M和R相关性带来的回归结果的不确定性，目前大多数衰减关系的回归分析都采用这种方法. 此后，王国新和陶夏新(2001)、 卢建旗等(2009)、 肖亮和俞言祥(2010)等也进行了这方面的研究.
从统计学角度来看，样本分布的不均匀同样会造成统计结果的不稳定． 为此，Campbell(1981)考虑到地震记录中M和R分布不均匀的情况，在回归分析中引入权重，将地震记录按距离分档，各档中不同地震记录的权重为1/nij(其中nij表示j档中i地震的记录数)． 这种权重的取法更多地考虑了在距离分档下，不同地震的记录分布不均匀的情况． 霍俊荣和胡聿贤(1992)分别对M和R进行分档，对有记录的各分档区间[ΔM，ΔR]赋予等权，每个区间内的记录又具有相等的权重1/n(其中n为该区间内数据的总和)． 这种方法虽比Campbell(1981)的方法有所改进，但却未考虑区间内不同地震记录分布不均匀的情况． 以上两种方法都只限于一步法的回归分析，本文将提出一种考虑样本分布不均匀的加权两步回归法．
1. 方法介绍
本文重点在于研究样本分布不均匀对回归分析的影响. 为方便比较，仍采用Joyner和Boore(1981)的衰减模型及记录数据. 两步法的第一步以距离为变量，回归参数中包含Ai这个随地震变化的参数． 首先，将地震记录按距离分档，每个记录得到的权重为w′ij=1/(njni)(其中nj为该记录所在档的地震数，ni为该记录的地震在此档中的记录数)． 为保证自由度的相同，将权重标准化，即wij=w′ijn/j(其中n为总记录数，j为分档数)． 这种权重的取法不仅使各档的权重相同，而且保证各档中不同地震也获得相同的权重． 最终得到一个权重的对角矩阵： W=diag[W1，W2，…，Wj，…，Wn](其中Wj为第j条记录对应的标准化后的权重)． 第一步的回归为非线性回归，将式(1)按Draper和Smith(1998)的关于非线性回归方法线性化，有
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
第二步，将地震按震级分档，每次地震得到的权重为v′k=1/nk(其中nk为该地震所在档的地震数)． 为保证自由度一致，将权重标准化，即vk=v′kN/k(其中N为地震总数，k为分档数)． 同样得到一个权重的对角矩阵： V=diag[V1，V2，…，Vi，…，VN](其中Vi为第i次地震对应的标准化后的权重)． 对式(2)进行加权线性回归得到以下结果：
第一步方差的无偏估计值为
第二步方差的无偏估计值为
总方差为
2. 算例
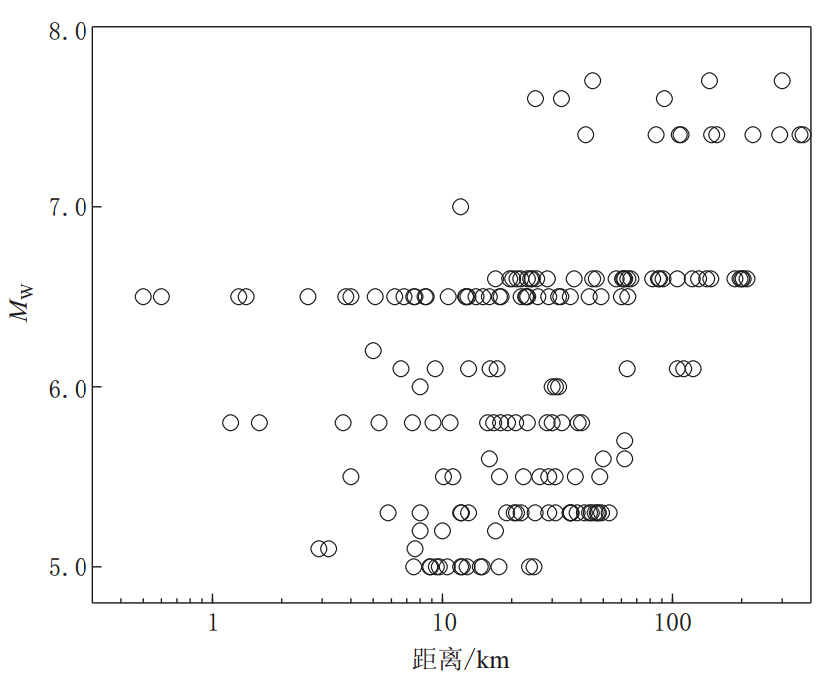
Joyner和Boore(1981)采用的峰值加速度记录共182条，取自23次不同的地震． 图 1及表 1清楚地表明，样本在震级和距离的分布上很不均匀．
![]()
图 1 峰值加速度记录的震级与距离分布图(修改自Joyner，Boore，1981)Figure 1. Distribution of PGA recordings with respect to magnitude and distance(modified after Joyner，Boore，1981)表 1 用于回归分析的地震及记录数Table 1. Earthquakes used for regression analyses and number of recordings
将地震记录按距离分成12档，每档在对数坐标下保持间隔一致，具体分档见表 2． 权重的取法按照上面第一步的方法进行. 例如，6.1—10.0 km档中，有8次不同的地震，1966年帕克菲尔德地震有2个记录，这两个记录的权重w′为1/16，标准化后的权重w=w′×182/12=91/96． 得到对角权重矩阵后按照式(3)—(6)进行迭代回归分析，直到拟合出理想的结果．
表 2 距离分档表Table 2. Distribution of recordings by distance
为降低回归分析的不确定性，在第二步分析中去掉6次只有单一记录的地震，对剩下的17次地震进行分档，按震级在普通坐标系下等间距划分，具体分档见表 3． 由于MW7.0—7.3没有地震，总档数为6． 按照上面第二步中计算权重的方法取权重. 例如，MW5.8—6.1档中总共有4次地震，该档中各地震的权重v′为1/4，标准化后的权重v=v′×17/6=17/24． 得到权重对角矩阵后，按照式(7)—(10)进行加权线性回归，拟合出参数a，b的值，其回归结果见表 4.
表 3 震级分档表Table 3. Distribution of recordings by magnitude
表 4 回归参数及标准差Table 4. Regression parameter and standard deviation
3. 结果分析与比较
表 4为加权两步法的回归结果，其回归方差与未加权的Joyner和Boore(1981)两步法(以下称之为传统两步法)的差别很小，而回归参数中最大的差别源于b值和d值．
图 2为Ai与震级的关系图. 回归参数b为图 2第二步回归中一元线性回归直线的斜率. MW5.0—6.0的地震在回归过程中几乎占到了样本的一半，而它们的分布与整体的样本分布并不一致. 在传统两步法的第二步回归中，该部分被赋予较高的权重，从而“拉”低了直线的斜率，导致大于样本平均值震级地震的拟合值偏小(该值为第一步回归分析中Ai的拟合值，反映了近场地震动的大小). 震级的增大会引起偏差的增大，反之亦然． 而采用按震级加权的方法后该部分的权重降低，b值由0.249增大到0.281．
![]()
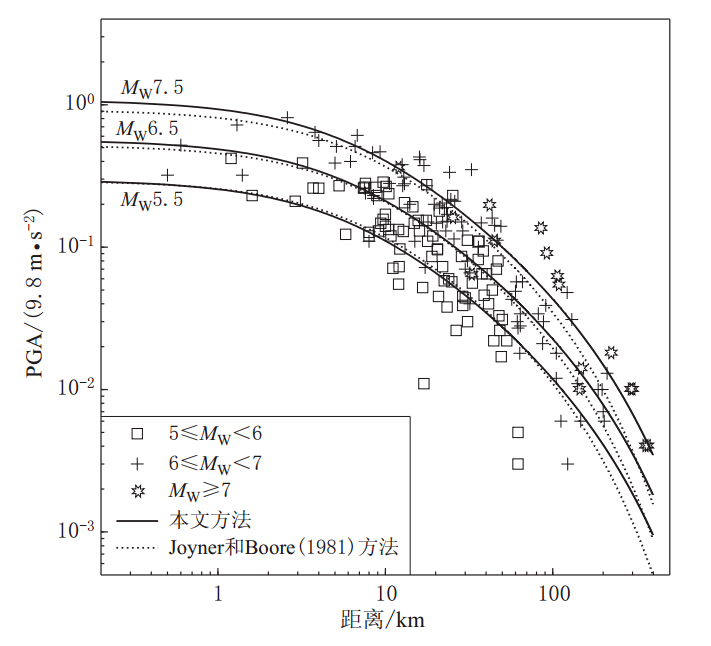
图 2 Ai-MW关系图The blocks represent the events in the second step regression, the stars represent the six events not involved in the second step regression, the straight line represents the fitted curveFigure 2. Values of Ai against magnitude MW图 3为传统两步法与加权两步法拟合衰减曲线的比较及散点分布图. 如图 3所示，对于小震级，传统两步法拟合的近场峰值加速度值稍大于加权两步法，而大震级情况下则相反，且随着震级的增大，这种差距有增大趋势. 这与上面的分析结果一致．
![]()
图 3 传统两步法与加权两步法拟合衰减曲线比较及散点分布图Figure 3. Comparison of attenuation curves by traditional two-step method and weighted two-step method with scatter diagram由于lgr的系数在模型中设定为-1，所以d在很大程度上反映了不同回归方法得到的衰减关系在远场的衰减速度． d是第一步的回归参数. 传统两步法的第一步对每条记录采用相同的权重，由于本数据库中远场的记录很少，远场的地震动估计值会受记录较多的近、 中场记录的影响，从而导致远场的衰减速度过快． 图 3中，Kern County MW7.4地震大于300 km的两个记录在传统两步回归法的MW7.5衰减曲线的外侧； 而加权后这些点的权重增加，d值由-0.00255增加到-0.00171，远场的衰减速度变慢，而以上的两个点也到了回归曲线的内测. 表明加权两步法拟合的衰减关系曲线与记录的空间分布更加吻合．
从图 3还可以看出，在10—50 km的区间内，记录点分布十分密集． 据表 2统计，该区间内共有101条记录，约占总记录数的55.5%． 在第一步分析中，引入权重后，该区间内记录点的权重大幅度降低，而加权两步法得到的衰减曲线与传统两步法得到的衰减曲线却非常接近． 这说明，加权回归分析对于数据分布较为密集区域的回归结果影响较小，同时也说明在大样本空间下，回归结果是比较可靠的．
以上分析表明，数据样本分布的不均匀对回归的结果有很大影响，在回归过程中须加以考虑．
最后还需指出，利用本文方法在数据分析前一定要作好噪声数据的甄别工作． 如果被视为噪声的记录或地震被赋予较高的权重，回归的结果势必会向更加偏离真实地震动分布的方向发展． 本文虽未涉及到这方面的内容，但在第二步的分析中首先去除了只有1次记录的地震． 第二步的分析是以震级为对象，分析过程中，这些记录的权重会大大增高，从而增加了结果不确定的可能性．
4. 结论
样本分布的不均匀会造成衰减关系的回归结果不能准确地反映地震动的空间分布规律. 本文分别考虑回归样本中震级、 距离以及不同地震记录数分布不均匀的情况，在两步回归法中引入样本的权重． 结果表明，考虑了这些因素的回归结果比传统两步回归法的结果能更准确地反映地震动的空间分布．
本文重点在于分析样本分布不均匀对两步法回归分析的影响. 以Joyner和Boore(1981)的数据为分析对象进行加权两步法的回归，并与传统两步法回归结果进行比较. 结果表明: 传统两步法在近场拟合的小震峰值加速度的估计值偏大，大震的峰值加速度估计值偏小，其衰减曲线在远场的衰减速度过快； 而加权两步法则能更好地反映地震动的空间分布规律． 本文的回归模型并未考虑诸如震级的近场饱和、 场地效应等地震动特性，而它们只能通过模型的形式来体现，最新的衰减关系模型大都考虑了这些特性． 相信在今后的工作中用加权两步法分析新的衰减模型，同样能够得到理想的结果． 特别需要注意的是，利用该方法进行回归分析前，一定要作好噪声样本的甄别工作．
-
![]()
图 1 峰值加速度记录的震级与距离分布图
(修改自Joyner，Boore，1981)
Figure 1. Distribution of PGA recordings with respect to magnitude and distance
(modified after Joyner，Boore，1981)
![]()
图 2 Ai-MW关系图
The blocks represent the events in the second step regression, the stars represent the six events not involved in the second step regression, the straight line represents the fitted curve
Figure 2. Values of Ai against magnitude MW
![]()
图 3 传统两步法与加权两步法拟合衰减曲线比较及散点分布图
Figure 3. Comparison of attenuation curves by traditional two-step method and weighted two-step method with scatter diagram
表 1 用于回归分析的地震及记录数
Table 1 Earthquakes used for regression analyses and number of recordings
下载: 导出CSV
-
霍俊荣, 胡聿贤. 1992. 地震动峰值参数衰减规律研究[J]. 地震工程与工程振动, 12 (1): 1-11. Huo J R, Hu Y X. 1992. Study on attenuation laws of ground motion parameters[J]. Earthquake Engineering and Engineering Vibration, 12 (1): 1-11 (in Chinese).
卢建旗, 李山有, 李伟. 2009. 改进的两步法在地震动衰减关系建立中的应用[J]. 世界地震工程, 25 (3): 46-48. Lu J Q, Li S Y, Li W. 2009. Application of improved two-step method on establishment of ground motion attenuation relationship[J]. World Earthquake Engineering, 25 (3): 46-48 (in Chinese).
王国新, 陶夏新. 2001. 地震动衰减关系拟合的新两步法[J]. 地震工程与工程振动, 20 (1): 24-28. Wang G X, Tao X X. 2001. A new two-steps method for fitting ground motion attenuation relationship[J]. Earthquake Engineering and Engineering Vibration, 20 (1): 24-28 (in Chinese).
肖亮, 俞言祥. 2010. 一种新的拟合地震动衰减关系的分步回归法[J]. 地震学报, 32 (6): 725-732. Xiao L, Yu Y X. 2010. A new step-regression approach for fitting ground motion data with attenuation relation[J]. Acta Seismologica Sinica, 32 (6): 725-732 (in Chinese).
Campbell K W. 1981. Near-source attenuation of peak horizontal acceleration[J]. Bull Seismol Soc Am, 71 (6): 2039 -2070.
Draper N R, Smith H. 1998. Applied Regression Analysis[M]. 3rd edition. New York: John Wiley & Sons, Inc. : 507-511.
Joyner W B, Boore D M. 1981. Peak horizontal acceleration and velocity from strong-motion records including records from the 1979 Imperial Valley, California, earthquake[J]. Bull Seismol Soc Am, 71 (6): 2011-2038.
-
期刊类型引用(2)
1. 丁佳伟，吕大刚，曹正罡. 考虑随机效应的Clough-Penzien功率谱参数预测模型及地震动合成. 振动与冲击. 2023(14): 260-269 . 
百度学术
2. 刘平，罗奇峰. NGA数据库的多圆组合地震动衰减模型. 哈尔滨工业大学学报. 2017(06): 164-170 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 566
- HTML全文浏览量: 270
- PDF下载量: 24
- 被引次数: 6
