Born approximation paradox of linear finite-frequency theory
-
摘要: 对有限频率层析成像线性理论的波恩近似问题进行梳理， 用数值方法统计分析其适用范围， 结果表明波恩近似要求最大速度扰动不超过1%； 然后对相关走时一阶近似进行统计分析， 结果表明它也只适用于最大速度扰动在1%以内的情形. 然而， 结合波恩近似和相关走时一阶近似而得到的有限频率线性理论， 其适用的速度扰动范围最大可达10%. 这个表面上的逻辑悖论， 称为“波恩近似佯谬”. 此佯谬是由于不恰当地使用波恩近似造成的. 本文摒弃波恩近似， 使用泛函的Fréchet微分和隐函数定理推导得到有限频率线性理论， 圆满解释了波恩近似佯谬. 由于有限频率非线性理论早已摒弃了波恩近似， 因此波恩近似概念在有限频率层析成像理论中完全没有必要.Abstract: After reviewing the Born approximation problem of linear finite-frequency tomography theory, its scope of application is statistically analyzed by numerical method. The result indicates that the maximum velocity perturbation should not exceed 1% for Born approximation. Then the statistical analyses on the first-order approximation of cross-correlation travel-time also show that it only meets the case of the maximum velocity perturbation less than 1%. However, the maximum velocity perturbation can be 10% for linear finite-frequency theory, which combines Born approximation with the first-order approximation of cross-correlation travel-time. This apparent logic paradox is called “Born approximation paradox”, which is caused by misusage of Born approximation. Thus, Born approximation is discarded in this study; Fréchet derivative and implicit functional theorem are used to deduce linear finite-frequency theory. As a result, Born approximation paradox is explained thoroughly. Since Born approximation has been discarded early in nonlinear finite-frequency theory, this concept is unnecessary in finite-frequency tomography theory.
-
引言
有限频率层析成像理论是最近十余年来地震层析成像的新理论． 传统的体波地震层析成像以射线理论为基础，要求地震射线的频率为无穷大． 对于短周期地震波，射线理论近似适用； 对于中长周期地震波，射线理论不太适用． Dahlen等(2000)提出了结合射线理论和波恩近似的三维体波有限频率走时层析成像理论. Zhao等(2000)建立了基于体波正则模型表述的有限频率层析成像理论. 之后，Zhao等(2005)提出散射积分方法. Tromp等(2005)及Liu和Tromp (2006)提出共轭波场法. Fichtner等(2008)提出时间-频率域的共轭波场反演方法． 有限频率层析成像理论对于任意频率的波都成立． 它还可以对地震波进行分频段滤波，提取多频段信息进行反演，从而充分利用宽频带地震资料，因此获得了广泛的应用(Montelli et al ，2004; Hung et al ，2005，2011； Yang et al ，2006; Chen et al，2007; Gautier et al ，2008; Tape et al ，2009，2010; Bezada et al ，2010; Fichtner et al ，2010; Liang et al ，2011； Liu et al ，2011)．
波恩近似源于量子力学中微观粒子弹性碰撞理论． 当入射粒子的动能比其势能大得多时，散射波场等于入射波场加上一个微扰波场． 这时，可以忽略散射方程中二级以上扰动项，获得散射波场的波恩近似解． 声波和弹性波的扰动问题，形式上与量子力学的高速粒子碰撞问题类似，因此波恩近似被借用来求解声波的介质扰动问题(Rayleigh,Strutt，1945; Wolf，1945)和弱非均匀介质的弹性波场扰动问题(Yamakawa，1956; Knopoff，1959; Miles，1960; Hudson，1977; Aki,Richards，1980; Wu,Aki，1985; Snieder，1986; Coates,Chapman，1990)． 有限频率层析成像线性理论(Dahlen et al ，2000; Zhao et al ，2000)的创立过程中，波恩近似扮演着重要的角色． 为了求得因介质参数扰动而导致的扰动波场，必须使用波恩近似略去与高阶扰动波场有关的项． 有限频率非线性理论一开始也使用了波恩近似(Tromp et al ，2005)，但很快就摒弃了它，而使用拉格朗日乘子法直接推导(Liu，Tromp，2006)．
微观粒子的碰撞是瞬态过程，只要粒子的势能远小于动能，波恩近似解就足够精确． 但地震波的传播却不是瞬态过程，速度扰动分布在-2%—2％，直观上会觉得这个扰动足够小． 但只要传播路径足够长，这么小的速度扰动累积的扰动波场也不再是小量，这足以导致波恩近似不成立． 波恩近似的成立条件需要用数值计算进行定量的统计分析． 但自从波恩近似被借用到地震学的弱非均匀介质问题以来，没有人对其适用范围做过定量分析． 建立在波恩近似基础上的有限频率线性理论，其数学基础并不严谨．
本文对有限频率线性理论的波恩近似问题进行梳理，用数值计算方法统计分析出其适用范围． 实际地球介质的反演问题，包括体波的走时、 幅度和 Q 值反演，以及面波的走时、 幅度、 偏振角、 群速和 Q 值反演． 本文选取应用较广的体波走时有限频率线性理论进行统计分析，比较其适用范围与波恩近似适用范围，发现了波恩近似佯谬． 最后，使用泛函分析方法来解决波恩近似佯谬，使有限频率层析成像理论建立在更为严谨的数学基础之上．
1. 波恩近似的适用范围
1.1 弱扰动问题的波恩近似解
三维非均匀介质的弹性动力学方程为
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
记初始模型的密度、 弹性系数张量和位移分别为ρ0，C0，u0，目标模型的的密度、 弹性系数张量和位移分别为ρ=ρ0+δρ，C=C0+δC，u=u0+δu． 它们的体力均为 f ． 总边界为S=Sa+Σ++Σ－，其中， Sa为自由表面边界，Σ+和Σ－为断层边界的正、负表面．
边界S围成闭区域⊕． 令 n 为闭区域表面的外法向量，v 是从边界负表面指向正表面的法向量． 在Sa和Σ－上，v = n ； 在Σ+上，v =- n ．再令 η 为断层滑动方向， ξ为边界上的二维坐标，T(u,ν) 为边界上的牵引力，在极限意义下 T(u,ν)=ν · (C∶u )．
在初始模型中
其边界条件和初始条件为
在目标模型中
其边界条件、 初始条件同初始模型，即
式(3)和式(8)表明断层面法向位移连续，故法向牵引力连续，即
由式(6)减去式(2)，得
由式(9)减去式(5)，得扰动波场的初始条件为
由式(7)减去式(3)，以及自由表面条件，得扰动波场的边界条件为
另外，由式(14)可推得
选取格林函数满足零初始条件和自由表面条件，且在断层面上格林函数及其导数连续，有
式(12)等号右边包含未知量δ u ，无法求解，需要先将等式右边化为已知量． 若介质参数符合小扰动条件
可假设波场的扰动符合波恩近似条件
则式(12)右边与未知量有关的二阶小量可略去，得
式(22)可以应用表示定理求解． 依据式(13)—(19)，得
式中，r S是震源位置矢量，r R是接收点位置矢量．
通过适当的等价变换(见附录)，最后可得
其中
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
将式(24)对时间变量t求导，可得三维非均匀介质中波恩近似条件下的速度扰动波场，即
其中
1.2 波恩近似的适用范围
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
震源有4个，为位错源，位于 y =-100 km的平面上． 震源时间函数的优势周期为2 s． 震源参数随机选取，如表1所示． 接收点25个，位于 y =100 km 的平面上，位置坐标如表2所示． P波速度为5.7 km/s，S波速度为3.4 km/s，密度为2.8× 103 kg/m3．
表 1 震源参数Table 1. Focal parameters
表 2 接收点参数Table 2. Receiver parameters
常用的震源时间函数有高斯型震源时间函数、 Ricker子波等． 这些函数的优点是有无穷阶连续导函数，缺点是不满足因果律，即在断层滑动之前和断层滑动停止以后速度都不为0． 这个缺点造成理论地震图有一定的计算误差． 为克服该缺点，本文提出九次多项式震源时间函数（其中Tm为优势周期），即
九次多项式震源时间函数的导函数为
式(27)严格满足因果律，从而减小了数值计算误差． 由于多项式的积分可以表达为有限形式，因而计算均匀初始模型中体波相关走时有限频率Fréchet核函数时，可将多重积分化简为单重积分，从而大大减小了计算量． 这种震源时间函数的四阶导函数连续，适于计算各种有限频率Fréchet核函数．
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
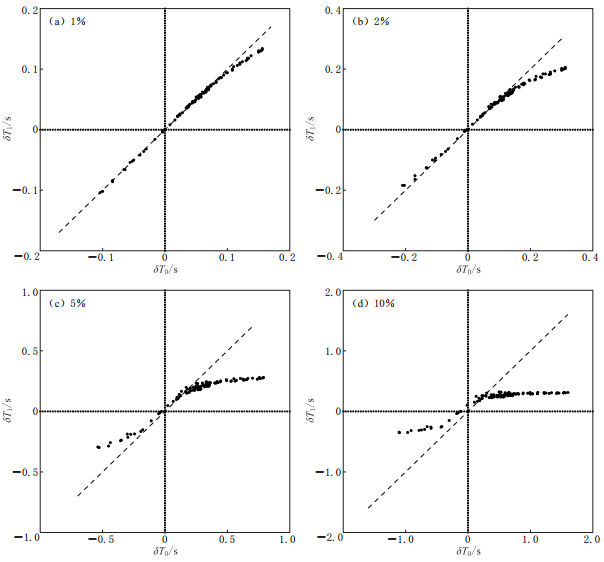
图2给出了目标模型的最大速度扰动分别为1%，2%，5%和10%的波恩近似相关走时误差图． 由图可见，速度扰动越大，误差越大． 最大速度扰动超过1%时，相关走时的误差已不可忽略． 只有当最大速度扰动小于1%时，误差才比较小． 本节只检验了走时的波恩近似条件． 若将幅度的波恩近似条件考虑进去，模型的最大速度扰动必须远小于1%． 波恩近似的数学本质是一阶线性近似． 这表明，对于实际的地震层析成像，波形反演是高度非线性的，这与地震学界一直以来的普遍认识相一致．
![]()
图 2 随机扰动情形下的波恩近似相关走时误差初始模型为均匀介质，目标模型为高斯型三维随机介质． 图(a)—(d)的最大速度扰动分别为1%，2%，5%和10%Figure 2. The errors of cross-correlation traveltime of Born approximation with random perturbations The starting model is homogeneous medium.The object model is 3-D Gaussian random medium. The maximum velocity perturbations of Figs.(a)—(d) are 1%，2%，5% and 10%，respectively2. 波恩近似佯谬
实际的地震层析成像，目标模型与初始模型的最大速度扰动一般都高于1%． 地壳上地幔的反演一般为3%—10%(Montelli et al，2004; Yang et al，2006; Chen et al，2007; Gautier et al，2008; Tape et al，2009，2010; Bezada et al，2010; Fichtner et al，2010; Hung et al，2011; Liang et al，2011； Liu et al，2011)． 可见，对于实际地震层析成像来说，波恩近似一般是不成立的． 但是，目前的有限频率层析成像线性理论又都以波恩近似为基础．究竟是有限频率线性理论隐含着巨大的漏洞，还是波恩近似只是个美丽的误会—佯谬？ 本节以体波的相关走时有限频率方法为例，对其进行深入分析．
2.1 相关走时一阶近似及其适用范围
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
对式(28)左边作泰勒展开，忽略二阶以上的高阶项，再令它等于0，作简单的变换(Dahlen et al ，2000)，可得相关走时的一阶近似公式，即
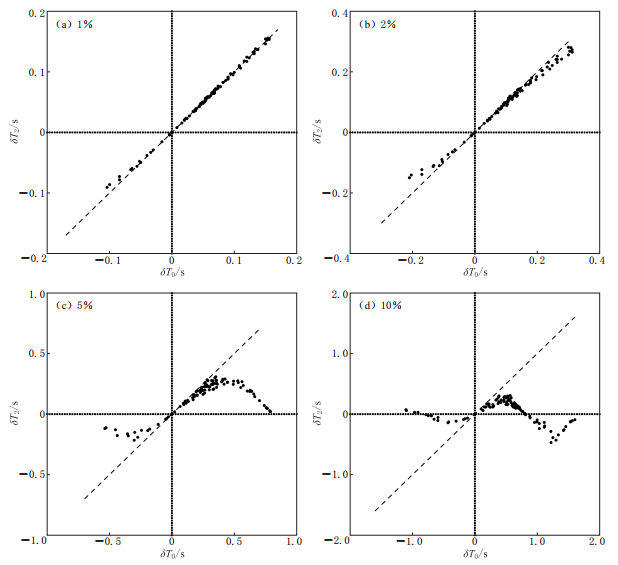
式(29)中的Δ (t)= (t)－ 0(t)，是扰动波场的精确值． 利用1.2节给出的震源和模型参数，类似地检验式(29)的适用条件，计算结果见图3．
![]()
图 3 随机扰动情形下相关走时泛函的一阶近似误差模型和震源参数同图2． 图(a)—(d)的最大速度扰动为分别为1%，2%，5%和10%Figure 3. The first-order approximation errors of the cross-correlation traveltime functional with random perturbationsThe parameters of the model and seismic sources are the same as those in Fig.2. The maximum velocity perturbations in Figs.(a)—(d) are separately 1%，2%，5% and 10%图3中，横坐标同图2，为相关走时的精确值; 纵坐标δT2为利用式(29)计算的一阶近似值． 由图3可见，当最大速度扰动超过1%时，相关走时的一阶近似带来的误差比较大； 当最大速度扰动超过5%时，误差比波恩近似误差还要大．
2.2 有限频率线性走时理论及其适用范围
把波恩近似与相关走时一阶近似结合起来，就可以获得有限频率线性走时理论的正演公式． 将式(29)中的Δ (t)用波恩近似δ (t)代替，得
考虑 e l分量，即δ (t) = e l · δ (t)，再将式(25)代入上式，交换时间和空间变量的积分次序，得
其中
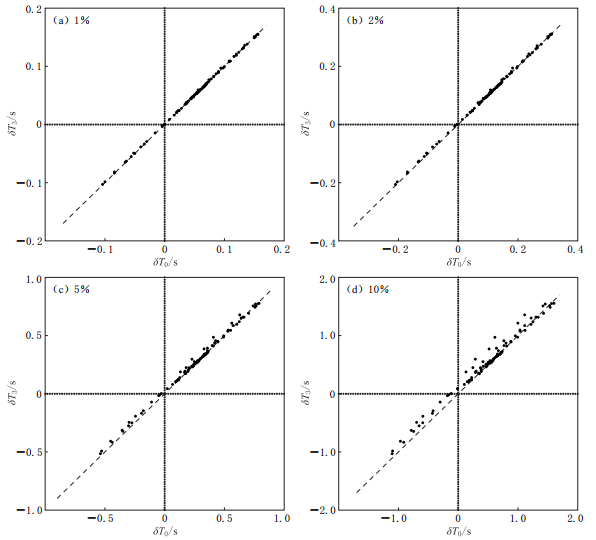
同样利用1.2节给出的震源和模型参数，可以检验式(30)的适用条件． 计算结果见图4．
![]()
图 4 随机扰动情形下有限频率方法的相关走时误差模型和震源参数同图2． 图(a)—(d)的最大速度扰动为分别为1%，2%，5%和10%Figure 4. The errors of the cross-correlation traveltime of finite-frequency theory with random perturbationsThe parameters of the model and seismic sources are the same as those in Fig.2. The maximum velocity perturbations in Figs.(a)—(d) are separately 1%，2%，5% and 10%由图4可见，当最大速度扰动在5％以内时，式(30)的误差可以忽略不计； 当最大速度扰动达到10%时，则有一定的误差． 但在图4d中，散点偏离斜率为1的直线的状态表现出整体平移的特征． 实际反演中，一般使用差异相关走时，整体平移的系统误差会被消除． 因此，图4d的误差仍然是可以忽略不计的．
Baig和Dahlen(2004)曾对声波的有限频率线性理论进行相关走时的误差统计． 结果表明，对于高斯型三维非均匀目标模型，只要最大速度扰动在10%以内，有限频率相关走时误差都比较小，这与本节的检验结果基本一致．
2.3 波恩近似佯谬
式(30)是由式(25)和式(29)推导来的． 一般情况下，推导结果的适用条件比推导过程的适用条件苛刻． 式(25)和式(29)的适用范围都是最大速度扰动不超过1%，但式(30)的适用范围却是最大速度扰动不超过10%，比前两者大得多． 这种表面上的逻辑矛盾，是由波恩近似造成的，本文称之为“波恩近似佯谬”． 造成波恩近似佯谬的原因，只有一种可能，那就是在任意一点上，式(25)引起的误差都被式(29)的误差基本抵消了． 从统计学的角度来看，随机误差逐点抵消是不可能的，只可能是系统误差的抵消． 因此，造成这种情况的原因，必定是推导过程存在理论错误． 若能绕过波恩近似，用另一种更严谨的方法推导出式(30)，那么波恩近似佯谬就能获得圆满解释．
3. 波恩近似佯谬的解决
式(30)中， KδT′ α，KδT′ β和KδT′ ρ分别是相关走时泛函关于α，β和ρ的Fréchet核函数． Luo和Schuster(1991)对声波方程求取相关走时Fréchet核函数的过程中，直接套用了数学分析中的隐函数求导法则． 用函数代替泛函的方法并不规范． 另外，他们在求波形Fréchet核函数仍然使用了波恩近似． 本节使用严格的数学方法，完全摒弃波恩近似，来推导有限频率线性走时理论．
3.1 泛函的Fréchet导算子
积分形式的多元泛函是多元非线性算子的一种形式，形如
其Fréchet导算子是如下线性积分算子：
式中，i = 1,2,…,n； h1( r ),h2( r ),…,hn( r ) 是给定的任意有界函数序列． 省略hi( r )，可写为
式中，i = 1,2,…,n. 式(31)是具有解析表达式的显泛函，故可以直接求导． 对于没有解析表达式的隐泛函，无法直接求导，需要使用隐函数定理．
多元算子隐函数定理的推论(郭大钧，2001)如下：
考察多元算子方程
若算子P及其一阶偏导算子P′ J(γ1,γ2,…,γn,J)在点(γ10 ,γ20 ,…,γn0 ,J0)的邻域内连续，则一阶偏导算子P′ γi(γ1,γ2,…,γn,J) (其中i = 1,2,…,n)在这点连续， P′ J(γ10 , γ20 ,…,γn0 ,J0)具有有界逆，则方程(34)在这点的Fréchet导算子为
式中，i=1,2,…,n. 若P的秩为1，则上式变为
3.2 波形Fréchet导算子
将式(12)等号右边关于δ u 的项移到左边，得
初始条件仍为式(13)． 依据式(14)和自由表面边条件，有
式(37)等号右边都是已知量，应用表示定理，得
式中 G ( r R,τ; r )是目标模型中点源的格林函数．
参照附录式(A1)—(A18)的推导过程，最后可得
其中,G = G ( r R, τ; r ),u 0= u 0( r ,t－τ; r S).
对于确定的 r S, r R,t, α0( r ), β 0( r )和ρ 0( r )，从式(41)可知扰动波形δ u 是δ α( r ), δ β( r ) 和δ ρ( r )的多元泛函，也就是α( r ),β( r )和ρ( r )的多元泛函． 经化简，可将式(41)写为
其中
由式(42)可见，式(41)是具有式(31)形式的显泛函．
利用式(33)和式(42)，可求出δ u (α, β,ρ) 的Fréchet导算子，即
在点(α0,β0,ρ0)处，有
由式(42)—(45)可求出δ u (α,β,ρ)在点(α0,β0,ρ0) 处的Fréchet导算子，即
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
3.3 相关走时Fréchet导算子
波形泛函δ u (α,β,ρ) 具有解析表达式，可直接求导． 而由式(28)确定的相关走时泛函δT(α,β,ρ)却没有解析表达式，只能用隐函数定理求导． 将式(28)视为多元算子方程
式中
对算子 P 求一阶偏导算子，得
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
上式表明，P′ δT[α0,β0,ρ0,0] > 0，故它的倒数存在，也就是有界逆存在． 因此，在点(α0,β0,ρ0)处，泛函δT(α,β,ρ)的一阶导算子可由式(36)、 式(54)和式(57)求得，即
将式(49)代入上式，交换积分次序，得
其中
KδT′ α就是相关走时泛函对P波波速的Fréchet核函数．
类似地，由式(36)、 式(55)和式(57)可得
其中
类似地，由式(36)、 式(56)和式(57)可得
其中
3.4 有限频率线性走时理论
由Fréchet微分的定义知
注意到δT(α0,β0,ρ0)=0，对上式作一阶近似，再将式(58)—(60)代入，并应用式(32)得
式(61)与式(30)完全一致． 从弹性动力学方程式(1)和相关走时的定义式(28)，用泛函的Fréchet微分法则得到式(61)的过程，没有用到波恩近似和相关走时一阶近似． 因此，图2和图3对于式(61)不构成约束． 式(61)是泛函δT(α,β,ρ)的一阶近似，与波恩近似和相关走时一阶近似无关． 其适用条件，亦即图4所示结果，与图2和图3无关．
至此，波恩近似佯谬获得圆满解决．
4. 讨论与结论
从波恩近似的源头上分析，与地震波的扰动问题相对应的微观粒子碰撞，应该是入射粒子在路径上发生一系列连续碰撞的波恩近似问题． 这种情形的波恩近似条件比单次碰撞要苛刻得多． 不加分析的概念借用，造成了波恩近似佯谬．
经过数值统计分析，可见波恩近似的适用范围和相关走时的一阶近似适用范围都很窄． 以P波走时为例，目标模型相对于初始模型的最大速度扰动不能超过1%，但有限频率线性理论的适用范围，却允许最大扰动达10%． 从逻辑上来说，推导过程的适用范围反而比推导结果的适用范围窄，这是一个悖论． 经过深入的分析，发现应用泛函的Fréchet微分，可以绕过波恩近似，直接导出有限频率线性走时理论． 因此，这个悖论是由于不恰当地使用了波恩近似造成的，是一个佯谬． 波恩近似佯谬表明，近十余年来，在有限频率层析成像线性走时理论中，普遍使用的波恩近似概念是不必要的误用． 对于最大速度扰动不超过10%的实际反演，波恩近似不成立，但有限频率层析成像线性理论是成立的． 由于有限频率非线性理论早已摒弃了波恩近似，因此波恩近似概念在有限频率层析成像理论中完全没有必要．
为了简化计算，本文初始模型选取均匀介质，只计算了P波的情形，选取有限频率相关走时方法进行统计分析． 对于其它类型的波，如S波、 面波，只需将P波格林函数换成相应类型波的格林函数即可． 对于体波幅度、 面波走时等有限频率方法，泛函的Fréchet微分法则一样适用． 因此，波恩近似佯谬在有限频率层析成像线性理论中具有普遍意义．
中国科学技术大学张伟为本文提供了有限差分程序，北京大学盖增喜和南京大学石亚龙与作者进行了有益的交流讨论，北京大学张献兵在并行计算程序方面提供了很多帮助，在此一并表示感谢．
附录 弱扰动问题波恩近似解的详细推导
下面给出本文1.1节中从式(23)到式(24)的详细推导过程．
令Sk+和Sk－为介质参数间断面的正、 负表面(k=1,2,…,N)．因闭区域⊕内部物质连续，故有连接条件
根据式(15)、 式(16)和式(A3)，在式(23)等号右边加上零项，则有
由式(11)减去式(10)，应用波恩近似条件，得
即
类似地，由式(8)减去式(4)，式(A2)减去式(A1)，作波恩近似，可得
将式(A5)—(A7)代入式(A4)，并注意到在负界面上 ν = n ，在正界面上 ν =－ n ，得
上式中Sg是由断层边界、 间断面和自由表面构成的总边界． 不妨将⊕视为被Sg分割成的若干个闭区域的总和，则由高斯定理可证明
证明如下：
不妨记 A = G 0( rR,τ; r )，B =δ C ∶u 0( r ,t－τ; rs)，则式(A9)等价于
由高斯定理知
将式(A11)代入(A10)，则式(A9)等价于
易证式(A12)恒成立，故式(A9)得证．
将式(A9)代入式(A8)，得
根据
得
各向同性介质中
将式(A14)和式(A15)代入式(A16)，化简后得
因此
故
因格林函数 G 0( rR,τ; r )在边界上满足齐次边界条件，由互易定理知
将式(A20)代入式(A19)，得
将式(A21)代入式(A13)，交换时间和空间变量的积分次序，忽略关于δ α，δ β和δ ρ的二阶以上高阶项，即得式(24)．
-
![]()
图 2 随机扰动情形下的波恩近似相关走时误差
初始模型为均匀介质，目标模型为高斯型三维随机介质． 图(a)—(d)的最大速度扰动分别为1%，2%，5%和10%
Figure 2. The errors of cross-correlation traveltime of Born approximation with random perturbations The starting model is homogeneous medium.
The object model is 3-D Gaussian random medium. The maximum velocity perturbations of Figs.(a)—(d) are 1%，2%，5% and 10%，respectively
![]()
图 3 随机扰动情形下相关走时泛函的一阶近似误差
模型和震源参数同图2． 图(a)—(d)的最大速度扰动为分别为1%，2%，5%和10%
Figure 3. The first-order approximation errors of the cross-correlation traveltime functional with random perturbations
The parameters of the model and seismic sources are the same as those in Fig.2. The maximum velocity perturbations in Figs.(a)—(d) are separately 1%，2%，5% and 10%
![]()
图 4 随机扰动情形下有限频率方法的相关走时误差
模型和震源参数同图2． 图(a)—(d)的最大速度扰动为分别为1%，2%，5%和10%
Figure 4. The errors of the cross-correlation traveltime of finite-frequency theory with random perturbations
The parameters of the model and seismic sources are the same as those in Fig.2. The maximum velocity perturbations in Figs.(a)—(d) are separately 1%，2%，5% and 10%
-
郭大钧. 2001. 非线性泛函分析[M]. 第2版. 济南: 山东科学技术出版社: 77-82. Guo D J. 2001. Nonlinear Functional Analysis[M]. 2nd ed. Ji'nan: Shandong Science and Technology Press: 77-82 (in Chinese).
Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods[M]. San Francisco: W H Freeman and Company: 721-751.
Baig A M, Dahlen F A. 2004. Statistics of traveltimes and amplitudes in random media[J]. Geophys J Int, 158(1): 187-210.
Baig A M, Dahlen F A, Hung S H. 2003. Traveltimes of waves in three-dimensional random media[J]. Geophys J Int, 153(2): 467-482.
Bezada M J, Levander A, Schmandt B. 2010. Subduction in the southern Caribbean: Images from finite-frequency P wave tomography[J]. J Geophys Res, 115(B12): B12333. doi:10.1029/2010JB007682.
Chen P, Zhao L, Jordan T H. 2007. Full 3D tomography for the crustal structure of the Los Angeles region[J]. Bull Seismol Soc Am, 97(4): 1094-1120.
Coates R T, Chapman C H. 1990. Ray perturbation theory and the Born approximation[J]. Geophys J Int, 100(3): 379-392.
Dahlen F A, Baig A M. 2002. Fréchet kernels for body-wave amplitudes[J]. Geophys J Int, 150(2): 440-466.
Dahlen F A, Hung S H, Nolet G. 2000. Fréchet kernels for finite-frequency traveltimes: I. Theory[J].Geophys J Int, 141(1): 157-174.
Fichtner A, Kennett B L N, Igel H, Bunge H P. 2008. Theoretical background for continental- and global-scale full-waveform inversion in the time-frequency domain[J]. Geophys J Int, 175(2): 665-685.
Fichtner A, Kennett B L N, Igel H, Bunge H P. 2010. Full waveform tomography for radially anisotropic structure: New insights into present and past states of the Australasian upper mantle[J]. Earth Planet Sci Lett, 290(3/4): 270-280.
Frankel A. 1986. Finite difference simulations of seismic scattering: Implications for the propagation of short-period seismic waves in the crust and models of crustal heterogeneity[J]. J Geophys Res, 91(B6): 6465-6489.
Gautier S, Nolet G, Virieux J. 2008. Finite-frequency tomography in a crustal environment: Application to the western part of the Gulf of Corinth[J]. Geophys Prospect, 56(4): 493-503.
Gee L S, Jordan T H. 1992. Generalized seismological data functionals[J]. Geophys J Int, 111(2): 363-390.
Graves R W. 1996. Simulation seismic wave propagation in 3D elastic media using staggered-grid finite differences[J]. Bull Seismol Soc Am, 86(4): 1091-1085.
Hudson J A. 1977. Scattered waves in the coda of P[J]. J Geophys, 43(1/2): 359-374.
Hung S H, Garnero E J, Chiao L Y, Kuo B Y, Lay T. 2005. Finite frequency tomography of D″ shear velocity heterogeneity beneath the Caribbean[J]. J Geophys Res, 110(B7): B07305. doi:10.1029/2004JB003373.
Hung S H, Chen W P, Chiao L Y. 2011. A data-adaptive, multiscale approach of finite-frequency, traveltime tomography with special reference to P and S wave data from central Tibet[J]. J Geophys Res, 116(B6): B06307. doi:10.1029/2010JB008190.
Knopoff L. 1959. Scattering of compression waves by spherical obstacles[J]. Geophysics, 24(1): 30-39.
Liang X F, Shen Y, Chen Y J, Ren Y. 2011. Crustal and mantle velocity models of southern Tibet from finite frequency tomography[J]. J Geophys Res, 116(B2): B02408. doi:10.1029/2009JB007159.
Liu K J, Levander A, Niu F L, Miller M S. 2011. Imaging crustal and upper mantle structure beneath the Colorado Plateau using finite frequency Rayleigh wave tomography[J]. Geochem Geophy Geosy, 12(7): Q07001. doi:10.1029/2011GC003611.
Liu Q Y, Tromp J. 2006. Finite-frequency kernels based on adjoint methods [J]. Bull Seismol Soc Am, 96(6): 2383-2397.
Luo Y, Schuster G T. 1991. Wave-equation traveltime inversion[J]. Geophysics, 56(5): 645-653.
Miles J W. 1960. Scattering of elastic waves by small inhomogeneities[J]. Geophysics, 25(3): 642-648.
Montelli R, Nolet G, Dahlen F A, Masters G, Engdahl E R, Hung S H. 2004. Finte-frequency tomography reavels a variety of plumes in the mantle[J]. Science, 303(5656): 338-343.
Rayleigh B, Strutt J W. 1945. The Theory of Sound[M]. New York: Dover Publications: 415-421.
Snieder R. 1986. 3-D linearized scattering of surface waves and a formalism for surface wave holography[J]. Geophys J Int, 84(3): 581-605.
Tape C, Liu Q Y, Maggi A, Tromp J. 2009. Adjoint tomography of the southern California crust[J]. Science, 325: 988-992.
Tape C, Liu Q Y, Maggi A, Tromp J. 2010. Seismic tomography of the southern California crust based on spectral-element and adjoint methods [J]. Geophys J Int, 180(1): 433-462.
Tromp J, Tape C, Liu Q Y. 2005. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels[J]. Geophys J Int, 160(1): 195-216.
Wolf A. 1945. Motion of a rigid sphere in an acoustic wave field[J]. Geophysics, 10(1): 91-109.
Wu R, Aki K. 1985. Scattering characteristics of elastic waves by an elastic heterogeneity[J]. Geophysics, 50(4): 582-595.
Yamakawa N. 1956. Investigation of the disturbance produced by spherical obstacles on elastic waves (I)[J]. Quart J Seism, 21(1): 1-12.
Yang T, Shen Y, van der Lee S, Solomon S C, Hung S H. 2006. Upper mantle structure beneath the Azores hotspot from finite-frequency seismic tomography[J]. Earth Planet Sci Lett, 250(1/2): 11-26.
Zhang W, Chen X F. 2006. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J]. Geophys J Int, 167(1): 337-353.
Zhang W, Zhang Z G, Chen X F. 2012. Three-dimensional elastic wave numerical modeling in the presence of surface topography by a collocated-grid finite-difference method on curvilinear grids[J]. Geophys J Int, 190(1): 358-378.
Zhao L, Jordan T H, Chaptman C H. 2000. Three-dimensional Fréchet differential kernels for seismic delay time[J]. Geophys J Int, 141(3): 558-576.
Zhao L, Jordan T H, Olsen K B, Chen P. 2005. Fréchet kernels for imaging regional earth structure based on three-dimensional reference models[J]. Bull Seismol Soc Am, 95(6): 2066-2080.
-
期刊类型引用(2)
1. 董阳，朴胜春. 基于声压敏感核的水下声场地声参数敏感性分析. 声学学报. 2024(05): 913-926 . 
百度学术
2. 董兴朋，滕吉文，马学英，宋鹏汉. 二阶Born近似有限频率走时敏感核. 地球物理学报. 2016(03): 1070-1081 . 百度学术
其他类型引用(1)
下载:
计量
- 文章访问数: 569
- HTML全文浏览量: 329
- PDF下载量: 35
- 被引次数: 3
