The seismic forward modeling using Born approximation equation based on rheological body
-
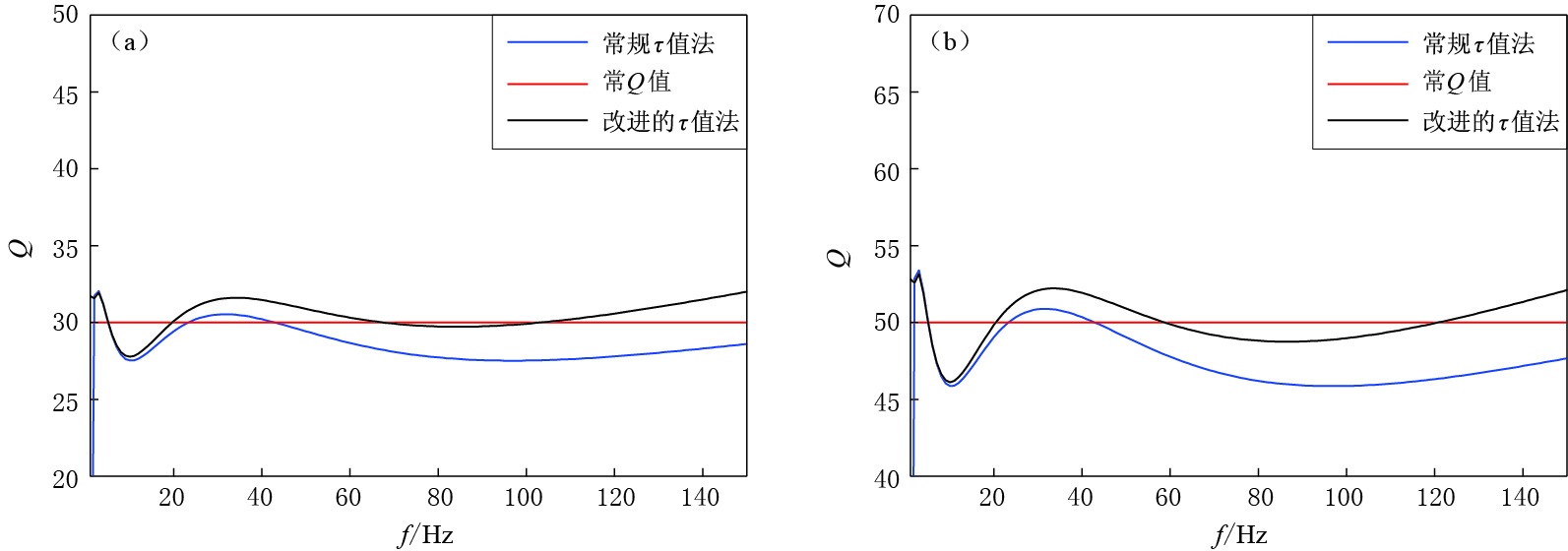
摘要: 常规τ值法假设应力松弛时间与应变延迟时间近似相等， 造成了常Q模型拟合精度低. 本文利用精确的广义流变体模型Q值计算公式, 研究改进的τ值法求解常Q模型参数. 根据地震波散射理论， 推导了基于广义流变体模型的黏滞性介质一阶波恩近似方程， 结合位移-速度关系得到了含卷积完全匹配层边界条件的黏滞性介质应力-速度方程的一阶波恩近似表达式. 通过数值实验验证并对比了黏滞性介质中全波波动方程、 一阶波恩近似方程以及单程波波动方程的波场特征， 讨论了基于流变体模型的黏滞性介质一阶波恩近似方程对速度扰动和Q扰动的适应性, 以及对旅行时和振幅精度的影响.Abstract: The conventional τ method assumes that the stress relaxation time is approximately equal to the strain delay time, leading to the constant Q model with low precision. In this study, an improved τ method is proposed by an accurate equation of Q value based on generalized rheological body so as to solve the parameters of constant Q model. According to the seismic wave scattering theory, the first-order Born approximation equation in viscoacoustic media is derived based on generalized rheological body and then the first-order Born approximation of stress-velocity equation is obtained for the viscoacoustic media with convolutional perfect matched layer (CPML) boundary. The wave fields and records are compared through numerical simulation by full wave equation, first-order Born approximation equation and one-way wave equation. And it is also discussed that the precision of travel time and amplitude of the seismic wave obtained by the viscoacoustic first-order Born approximation equation with velocity perturbation and Q perturbation.
-
Keywords:
- rheological body /
- Born approximation /
- improved τ method /
- velocity perturbation /
- Q perturbation
-
-
![]()
图 1 改进的τ值法与常规τ值法常Q模型拟合精度对比
(a) Q=30； (b) Q=50
Figure 1. Comparison of constant Q fitting by improved τ method with that by conventional τ method
(a) Q=30； (b) Q=50
![]()
图 2 弱速度扰动(a)和弱Q扰动(b)模型
Figure 2. The model with weak velocity perturbation (a) and weak Q perturbation (b)
![]()
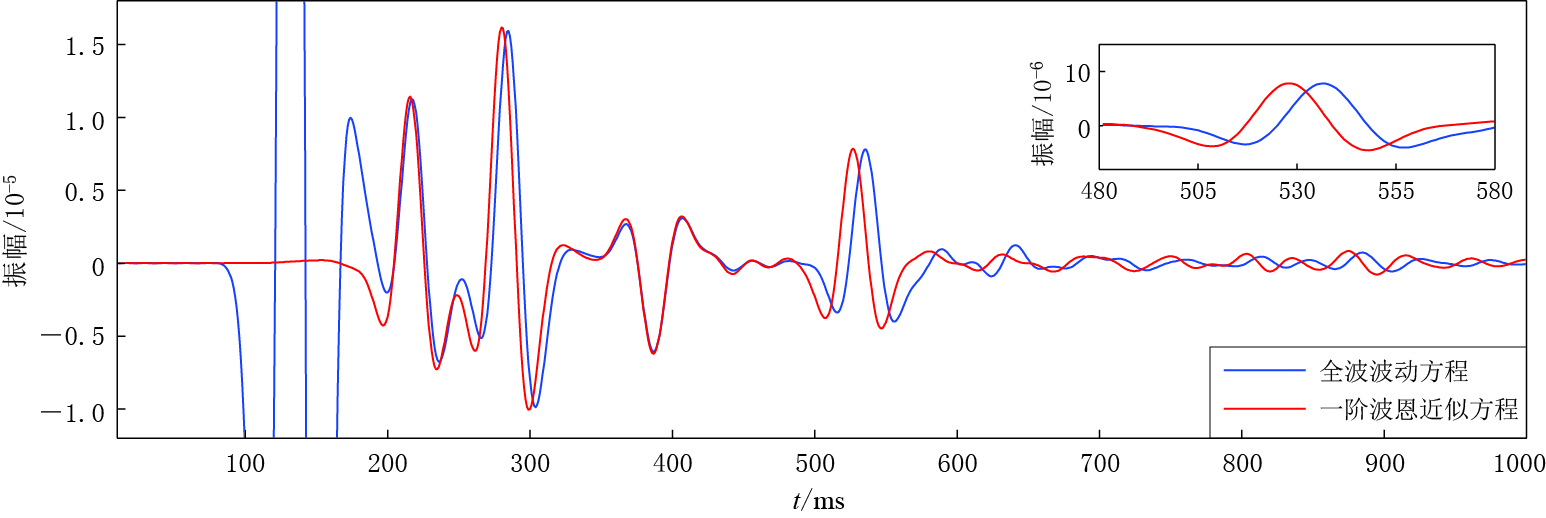
图 3 弱速度扰动及弱Q扰动模型中由全波波动方程(a，b)和一阶波恩近似方程(c，d)得到的黏滞性介质波场以及由全波波动方程与一阶波恩近似方程得到的波场差值(e， f)
(a)， (c)， (e)中t=420 ms； (b)， (d)， (f)中t=558 ms
Figure 3. The viscoacoustic wave fields obtained by different wave equations in the model with weak velocity perturbation and weak Q perturbation Figs.(a) and (b) are the wave fields obtained by full wave equation； Figs.(c) and (d) are the wave fields obtained by first-order Born approximation equation； Figs.(e) and (f) are the differences
between the wave fields in (a)， (b) and those in (c)， (d). In Figs.(a)， (c)，(e) t=420 ms and in Figs.(b)， (d)， (f) t=558 ms
![]()
图 4 黏滞性介质单程波波动方程得到的波场.
(a) t=420 ms; (b) t=558 ms
Figure 4. The wave fields obtained by one-way wave equation in viscoacoustic media
(a) t=420 ms; (b) t=558 ms
![]()
图 5 弱速度扰动及弱Q扰动模型中由全波波动方程(a)、 一阶波恩近似方程(b)和单程波波动方程(c)得到的地震记录
Figure 5. The seismic records obtained by full wave equation (a), first-order Born approximation equation (b) and one-way wave equation (c) in the model with weak velocity perturbation and weak Q perturbation
![]()
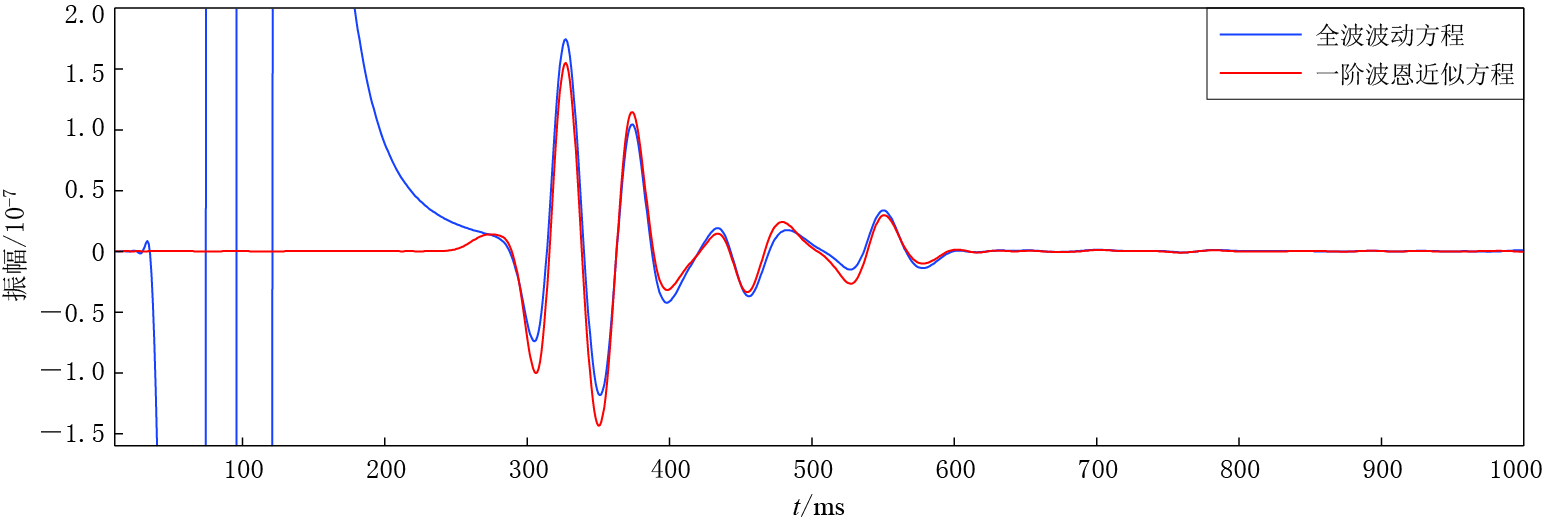
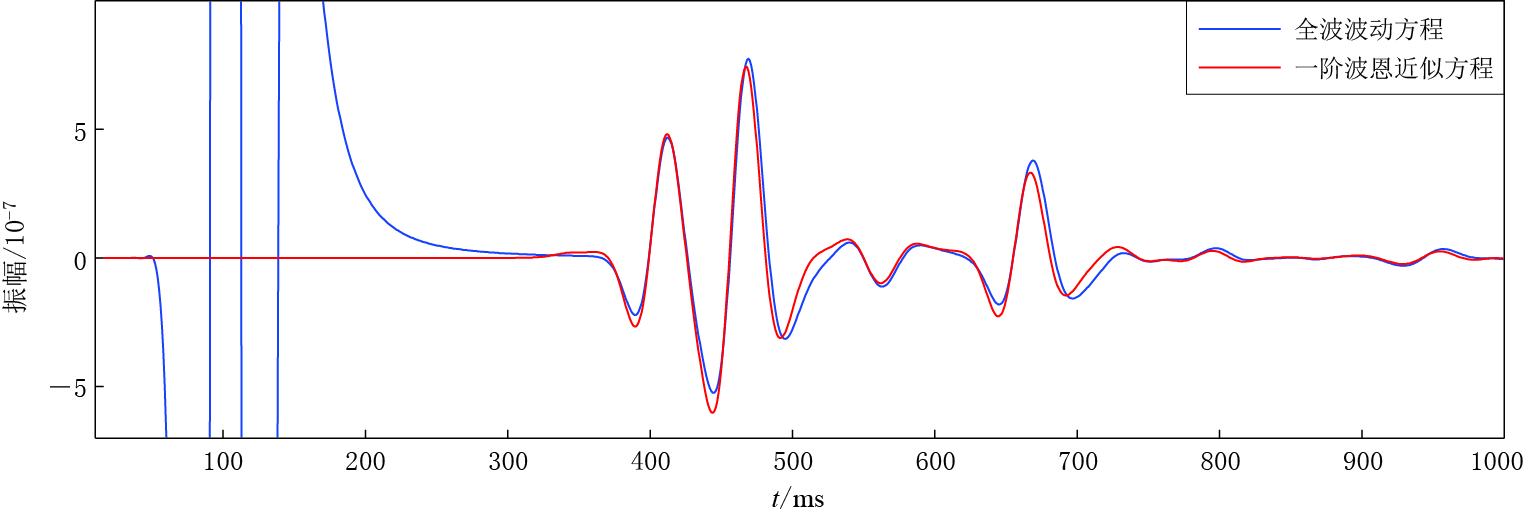
图 6 弱速度扰动及弱Q扰动模型中由全波波动方程、 一阶波恩近似方程与单程波波动方程得到的地震波形对比
Figure 6. Comparison of the seismic waveforms obtained by full wave equation (blue lines) with that by first-order Born approximation wave equation (red lines) and one-way wave equation (black lines) in the model with weak velocity perturbation and weak Q perturbation
![]()
图 8 强速度扰动及弱Q扰动模型中由全波波动方程(a)和一阶波恩近似方程(b)得到的地震记录
Figure 8. The seismic records obtained by full wave equation (a) and first-order Born approximation equation (b) in the model with strong velocity perturbation and weak Q perturbation
![]()
图 9 强速度扰动及弱Q扰动模型中由全波波动方程与一阶波恩近似方程得到的地震波形对比
Figure 9. Comparison of the seismic waveforms obtained by full wave equation (blue lines) with that by first-order Born approximation equation (red lines) in the model with strong velocity perturbation and weak Q perturbation
![]()
图 10 强Q扰动模型(a)和修改后的弱速度扰动模型(b)
Figure 10. The models with strong Q perturbation (a) and the modified weak velocity perturbation (b)
![]()
图 11 均匀速度场下强Q扰动模型中由全波波动方程与一阶波恩近似方程得到的地震波形对比
Figure 11. Comparison of the seismic waveforms obtained by full wave equation (blue lines) with that by first-order Born approximation equation (red lines) in homogenous velocity model with strong Q perturbation
-
曹丹平. 2008. 多尺度地震资料正反演方法研究[D]. 青岛: 中国石油大学(华东)地球科学与技术学院: 16-86. Cao D P. 2008. Method Research of Multiscale Seismic Data Modeling and Inversion[D]. Qingdao: School of Geosciences, China University of Petroleum (East China): 16-86 (in Chinese).
何兵红. 2011. 基于衰减介质的地震波数值模拟及吸收属性提取方法研究[D]. 青岛: 中国石油大学(华东)地球科学与技术学院: 36-50. He B H. 2011. The Study of Numerical Simulation of Seismic Wave in Attenuation Medium and Extraction of Absorption Properties[D]. Qingdao: School of Geosciences, China University of Petroleum (East China): 36-50 (in Chinese).
单启铜. 2007. 粘弹性波动方程正演模拟与参数反演[D]. 青岛: 中国石油大学(华东)地球科学与技术学院: 13-83. Shan Q T. 2007. Simulation and Inversion of Wave Equation in Viscoelastic Media[D]. Qingdao: School of Geosciences, China University of Petroleum: 13-83 (in Chinese).
吴如山. 1993. 地震波的散射与衰减[M]. 北京: 地震出版社: 49-80. Wu R S. 1993. Scatter and Attenuation of Seismic Wave[M]. Beijing: Seismological Press: 49-80 (in Chinese).
郑江峰. 2006. 粘弹性介质中提高地震资料分辨率方法研究[D]. 大庆: 大庆石油学院地球科学学院: 30-32. Zheng J F. 2006. Methodology and Research on Improving Seismic Resolution in Viscoelastic Media[D]. Daqing: Geoscience College, Daqing Petroleum Institute: 30-32 (in Chinese).
下载:
计量
- 文章访问数: 635
- HTML全文浏览量: 344
- PDF下载量: 23
