Discrimination of earthquakes and explosions by SAMC decision method
-
摘要: 在动态时间规整法的基础上, 建立了逐步代价最小决策法(SAMC). 该方法中的代价函数可以很好地反映特征归属, 对较差的特征具有一定的“容忍度”、 稳定性好, 还可用全程代价函数评判识别结果的可信度. 用SAMC方法对北京及其周边地区33次地震和29次爆破中提取的5个分类特征量进行识别, 识别率为90%; 从该5个特征量中选择较好的3个特征量进行识别, 识别率为92%; 在上述地区另选13次事件作为检验样本进行U检验, 5个分类特征量和3个分类特征量的识别率分别为92%和100%, 识别效果很好. 这表明SAMC是识别地震与爆破的有效方法.Abstract: Based on dynamic time warping (DTW) algorithm, this paper proposes a novel recognition algorithm, stepwise accumulating minimal cost (SAMC) decision method. By this method, each cost function can well reflect the tendency of event’s features; moreover, SAMC is unsusceptible to the quality of features. The absolute value of overall cost function can be also served as the reliability of the results. Five features were extracted for recognition from 62 events of earthquakes (33) and explosions (29) which occurred in Beijing and its peripheral regions. The result respectively reached 90% recognition rate for five features and 92% for three features which are better features from the five ones. In another testing by U-test, another 13 events (eight earthquakes and five explosions) were randomly chosen from the same area, and the recognition rate was 92% for five features and 100% for three ones. These suggest that SAMC method can be useful to discriminate earthquakes and explosions effectively.
-
引言
随着科技进步和经济的发展,人工爆破的数量越来越多,这为地震工作者的日常监测带来了新的挑战,如何准确、 快捷地识别天然地震与人工爆破显得十分重要. 近年来,国内外关于识别天然地震与人工爆破的研究很多,主要集中在两个方面: 第一,识别特征的研究. 例如,区域P/S二维网格数据的统计识别(Taylor,2011),利用小波分析或小波包变换得到的能量在时频域内的分布规律或高低频能量比特征(韩绍卿等,2010),快速识别天然地震与人工爆破的5种判据选择(王婷婷,边银菊,2011)等. 频谱方面特征还包括拐角频率、 峰值频率、 最大谱值和零频谱值、 倒谱、 谱比、 瞬态谱,以及波形的HHT等特征. 此外,传统的识别天然地震与人工爆破的震级比、 波形复杂度等特征也为广大科研人员所采用. 第二,识别算法的研究. 例如,用学习向量化(learning vector quantization,简写为LVQ)识别地震与爆破(边银菊,邹立晔,2002),遗传BP网络识别地震与爆破(边银菊,2002),将Fisher方法应用于mb/MS判据,定量地得出全球普适的识别方程(边银菊,2005),最近邻支撑向量特征线融合算法(李夕海等,2009),ν-SVC算法识别天然地震与爆破(黄汉明等,2010),SVM算法识别地震与爆破(毕明霞等,2011),基于无监督的自组织特征神经网络识别小震与爆破(Kuyuk et al, 2011),用决策方法识别地震与爆破(边银菊等,2012),等等.
从传统的最小距离分类法、 贝叶斯分类法发展到上述的遗传BP神经网络、 SVM算法等,地震与爆破识别算法的研究主要集中在统计模式识别领域中. 动态时间规整(dynamic time warping,简写为DTW)算法是统计模式识别中模板匹配类方法之一,最初被用来解决孤立词识别时的说话速度不均匀的问题,后经过发展,被国内外广泛用于声音、 文字、 图片的识别. 本文受该算法思路的启发,形成了逐步代价最小决策法,建立了识别爆破与地震的分类器. 应用该方法我们对北京及其周边地区的事件进行识别,取得了比较满意的效果.
1. 动态时间规整法和逐步代价最小决策法
动态时间规整法(DTW)定义两个序列: 一是参考模板的特征向量序列r(i),i=1,2,…,m; 二是测试模板的特征向量序列t(j),j=1,2,…,n. 将测试模板的特征向量序列通过某个路径投影到参考模板序列上,每一步的投影都对应着该步的代价函数d,投影结束后累计所有的代价函数得到全程代价函数D. 一般来讲,两个序列的长度不相等,即m≠n,所以,它们必须对齐或者弯折以对应匹配时所付出的代价. 最小的D所对应的路径称为最优路径.
找出所有的全程代价函数往往计算量很大,这里引入Bellman(1957)原理来解决. 假如(i,j)是原点(i0,j0)和终点(if,jf)路径上的一个节点,则Bellman原理可以用公式(1)来描述.

即从原点(i0,j0)经过节点(i,j)到终点(if,jf)的最优化路径,是由原点(i0,j0)到节点(i,j)的最优化路径与由节点(i,j)到终点(if,jf)的最优化路径的串联. 式中,表示串联.
最优化路径确定后,参考模板的特征向量序列与测试模板的特征向量序列的对应关系也就确定了下来,并据此来识别测试模板.
关于动态时间规整法(DTW)和Bellman原理的详情可参考Theodoridis和Koutroumbas(2009)所著的《Pattern Recognition》一书.
动态时间规整法的宗旨,即找到从测试模板到参考模板的最佳投影路径,评判最佳的标准是全程代价函数D为最小. 如果我们将待判样本特征作为测试模板,把测试模板类别作为参考模板,通过确定某种量化标准将样本类别和样本特征的关系进行量化. 对于二类分类问题,距离A类关系越近,值越小; 距离B类关系越近,值越大. 每个样本都有自己的关系序列,我们把所有的关系“相加”,就可以得到最优的“路径”. 这里的路径是指对象的各个特征的倾向组合. 最后根据D的值确定二类分类问题的分类器.
假如存在两种类别的序列r1(i)和r2(i),i=1,2,…,n,分别属于A类和B类,定义参考模板为r=(A类、 AB类、 B类),其中,AB类是指无法分类的类别. 判断某一测试序列t(i)的类属. 定义代价函数为

式中,a>c>b; a,b,c为常数. 当d(i)=a时,测试序列的第i个特征距离A类关系较近,规定其属于A类; 当d(i)=b时,测试序列的第i个特征距离B类关系较近,规定其属于B类; 当d(i)=c时,测试序列的第i个特征距离A类和B类的关系相同,则规定其属于AB类.
累积所有的代价函数,得到全程代价函数D,很容易得到D的取值范围为[nb,na]. D越大,测试序列距离A类序列越近,属于A类的可能性越大; D越小,则测试序列距离B类序列越近,属于B类的可能也越大.
但测试序列中的每一项并非一定全倾向于同一类别的序列,因此,全程代价函数D应该介于na与nc之间或nb与nc之间. 规定当na>D>nc,测试序列归为A类; 当nc>D>nb,测试序列归为B类. 综上,我们得到最终的分类器为

代价函数的定义可以保证从测试模板向参考模板投影的每一步都是最优的,根据Bellman(1957)原理,最终路径就是最佳的路径. 参考模板由一系列数值组成的特征序列变为由一系列类别组成的序列,即参考模板r=(A类、 AB类、 B类). 识别的对象从序列中的某一项变为识别某一序列的类别.
本文将上述思想引入天然地震与人工爆破的识别领域,建立了逐步代价最小决策法(stepwise accumulating minimal cost,简称SAMC). 该方法通过定义代价函数实现路径最优化,从而求得全程代价函数. 从全程代价函数出发来区分天然地震与人工爆破. 建立SAMC方法的主要步骤有:
1)识别地震与爆破的特征(或判据)提取. 从已知类别的事件文件中提取能够区分天然地震与人工爆破的各种特征. 分析每一项特征,找到最优分类阈值.
2)确定参考模板和测试模板. 根据特征的分布情况提取参考序列,包括爆破序列、 地震序列和阈值序列; 从学习样本集中提取同样的特征组成测试序列. 由参考序列的种类确定性质参考模板r=(爆破、 阈值、 地震),并规定测试序列即为测试模板.
3)建立分类器. 定义代价函数d(i)为

考虑到每项特征识别爆破与地震的效果不同,如果在计算代价函数d的时候将每一步等权重对待的话,势必影响最终的识别结果,因此,我们将学习样本集中单特征的识别率进行归一化后作为该步的权重来调整代价函数. 然后,计算全程代价函数值

式中,σi表示第i项特征的归一化后的识别率.
最后确定分类准则.考虑到参与识别的5个特征是串联起来的和每一步的代价函数的定义,理论阈值应该为0,故得到的分类器为

4)检验. 用测试模板的全程代价函数值根据相应事件的性质(地震还是爆破)按分类准则做出判别,得到检验结果,并计算检验样本集的识别率.
2. 资料选取与特征提取分析
2.1 资料的选取
本文选取的资料来自《北京数字遥测地震台网地震月报目录》和《北京数字遥测地震台网非天然地震月报目录》.
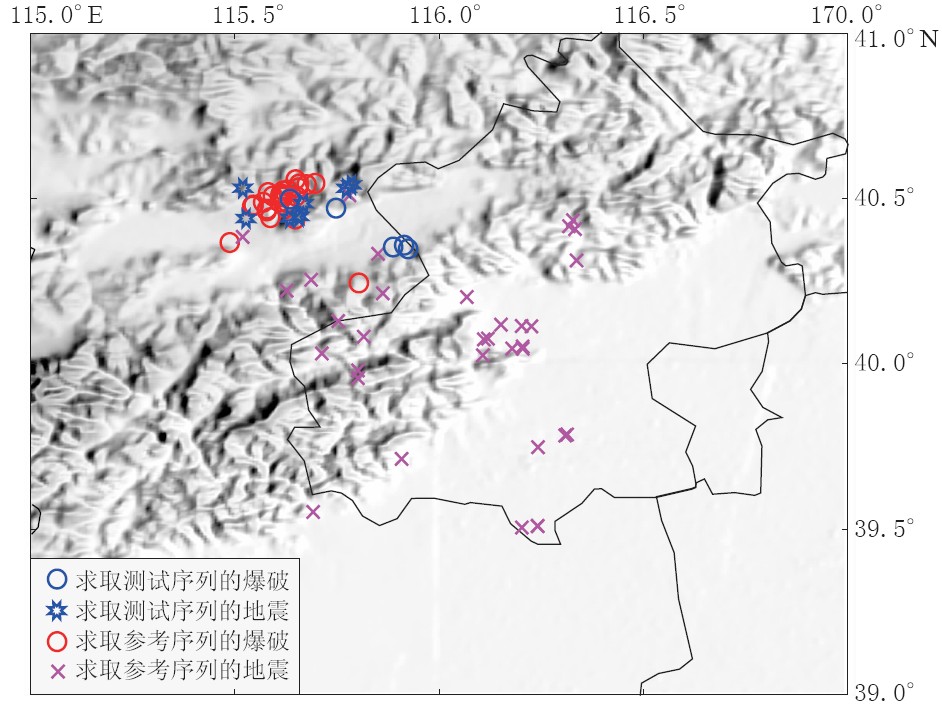
第一部分资料选取北京及其周边地区2002—2010年的29次人工爆破和2003—2007年的33次天然地震(人工爆破震级范围为1.0≤ML≤2.5,天然地震的震级范围为1.3≤ML≤3.2; 天然地震的深度范围为4—18 km,但大部分深度为8 km±1 km; 所选事件的地理范围为39.5°—40.6°N,115.0°—117.0°E). 这部分资料(学习样本集)主要用于学习,求取参考模板. 第二部分波形资料选取北京及其周边2009年2月—2010年9月的8次天然地震和2011年1—8月的5次人工爆破(天然地震的震级范围为1.6≤ML≤2.6,人工爆破震级范围为1.7≤ML≤2.0; 天然地震的震源深度为5—10 km; 所选事件的地理范围为40.3°—40.6°N,115.2°—115.9°E). 该部分资料(检验样本集)主要用于特征提取、 形成测试模板,以用于检验. 上述所选事件位置分布见图 1所示.
2.2 特征提取分析和特征模板形成
根据快速识别要求,我们选择的特征有P波初动方向,P波初动振幅与S波最大振幅之比(AP1/ASmax),P波最大振幅与S波最大振幅之比(APmax/ASmax),P波最大振幅与尾波持续时间之比(APmax/tme),以及S波最大振幅与尾波持续时间之比(ASmax/tme)等(王婷婷,边银菊,2011). 对所有事件资料选择垂直分量并提取上述5项特征. 初动方向量化处理根据王婷婷和边银菊(2011)提出的初动判据准则来确定,其它4到种特征取所有台站的平均值以减少台站分布的影响.
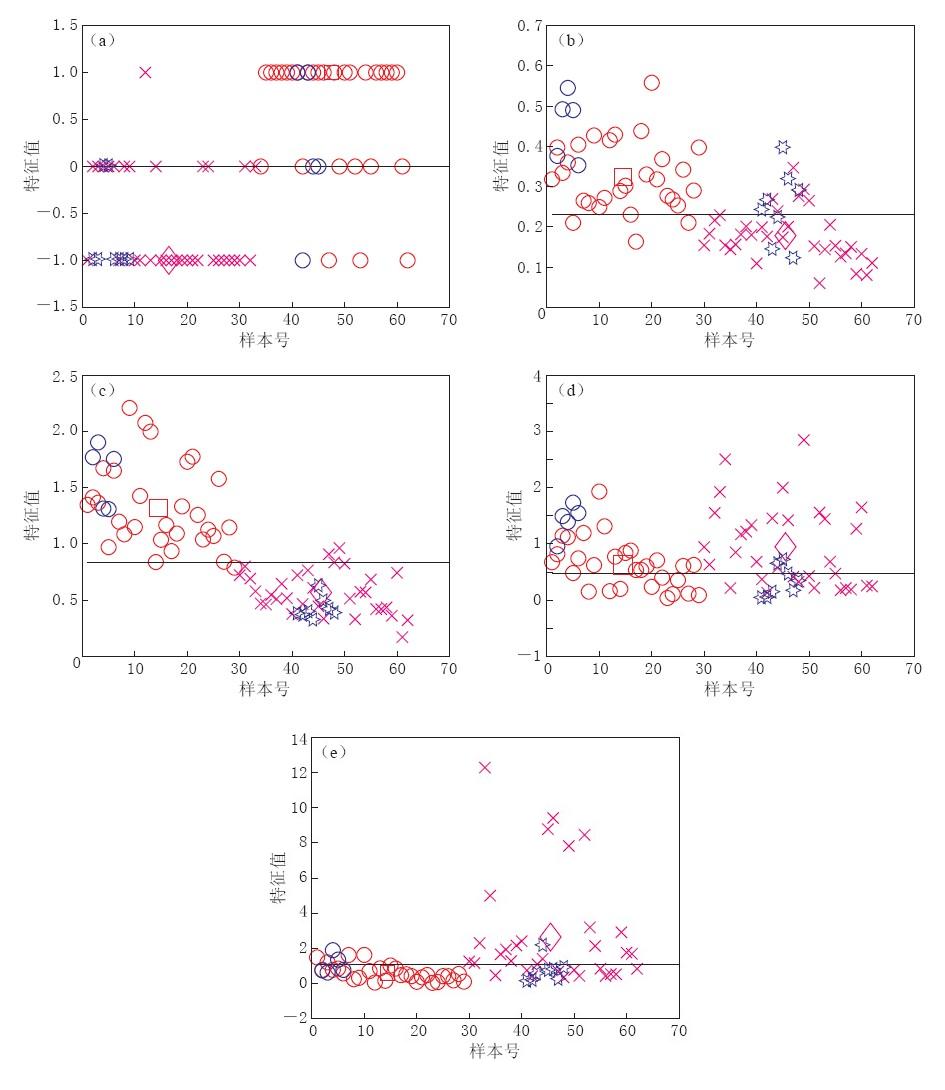
根据初动准则很容易判断初动方向的阈值为0. 其余4项特征,采用逐点计算误识率的方法,取误识率最小的值作为该特征的分类阈值. 图 2分别给出了这5项特征的阈值分析结果.
![]() 图 2 人工爆破与天然地震识别量的阈值分析(a) P波初动方向; (b) AP1/ASmax ; (c) APmax/ASmax; (d) APmax/tme; (e) ASmax/tme 红色圆圈和叉号分别表示学习样本集中的爆破与地震事件; 正方形和棱形分别表示学习样本集中爆破与 地震各项特征的重心; 蓝色圆圈和六角星表示检验样本集中的爆破与地震事件Figure 2. Thresholds for discriminating the explosions and earthquakes(a) P-wave first motion; (b) The ratio of P-wave first motion amplitude to the maximum amplitude of S-wave; (c) P/S maximum amplitude ratios; (d) The ratio of P-wave maximum amplitude to duration; (d) The ratio of S-wave maximum amplitude to their duration. The red circles and crosses represent explosions and earthquakes for learning, respectively; the squares and the diamonds represent template of each feature belonging to explosions and earthquakes, respectively; the blue circles and the hexagrams separately represent explosions and earthquakes for testing
图 2 人工爆破与天然地震识别量的阈值分析(a) P波初动方向; (b) AP1/ASmax ; (c) APmax/ASmax; (d) APmax/tme; (e) ASmax/tme 红色圆圈和叉号分别表示学习样本集中的爆破与地震事件; 正方形和棱形分别表示学习样本集中爆破与 地震各项特征的重心; 蓝色圆圈和六角星表示检验样本集中的爆破与地震事件Figure 2. Thresholds for discriminating the explosions and earthquakes(a) P-wave first motion; (b) The ratio of P-wave first motion amplitude to the maximum amplitude of S-wave; (c) P/S maximum amplitude ratios; (d) The ratio of P-wave maximum amplitude to duration; (d) The ratio of S-wave maximum amplitude to their duration. The red circles and crosses represent explosions and earthquakes for learning, respectively; the squares and the diamonds represent template of each feature belonging to explosions and earthquakes, respectively; the blue circles and the hexagrams separately represent explosions and earthquakes for testing根据震源机制判断,爆破是膨胀源,初动应该向上; 而地震是剪切源,初动可能向上,也可能向下. 从图 2a来看,地震事件中初动不清和初动向下的样本占多数,而爆破事件多数样本初动向上.
爆破的能量瞬间释放,P波幅值大,震动衰减快. 虽然爆破产生的S波机制尚未确定,但无论从“破裂说”还是“各向异性说”(Sammis et al,2008)来讲,S波的能量都小于P波能量,因此幅值较小. 相比而言,地震一般都是从小破裂开始,逐渐产生大的岩石错动,因而P波幅值小,S波幅值大. 故P波幅值与S波幅值之比是识别人工爆破与天然地震的较好判据之一. 从图 2b,c来看,爆破群与地震群被较好地分开了.
一般而言,尾波的持续时间随震级增大而变大. 波形最大幅值也是表征震级的物理量,因此,最大幅值与尾波持续时间之比,可以消除不同事件震级不同所造成的影响(王婷婷,边银菊,2011). 从图 2d,e看出,两种特征的识别率都不太理想,这可能是因为: ① 地区差异引起的噪声信号延长尾波时间,造成有些爆破事件的持续时间较长; ② 事件(尤其是爆破)的震级较小,噪声的干扰较大,因而尾波持续时间的测量误差较大.
通过上述特征分析及下面的方式可得到测试模板和参考模板.
1)测试模板.测试模板是用来检测模板类型的. 除初动特征按初动准则确定外,把每一个待测事件中所有台站提取特征后,取各个特征的平均值,初动特征和各个特征的平均值组成该待测事件的测试序列,把该测试序列定为测试模板.
2)爆破序列、 阈值序列和地震序列. 各种序列的形成步骤相同. 将学习样本中的所有爆破事件按照测试序列的提取过程提取就可以得到爆破序列,同样也可以得到地震序列; 取各个特征的分类阈值组成阈值序列. 参考模板是由一系列性质类别组成,定义参考模板为r=(爆破、 阈值、 地震).
由于特征之间是相互独立的,因此,累积代价函数可以任意排序. 单特征识别率不同决定了每个特征在全程代价函数中所占的比重也不相同,因此我们把经过归一化后的单特征的识别率作为权重调整全程代价函数. 表 1列出了各项单特征的识别率以及归一化后的值.
表 1 每一步权重值σTable 1. Weight σ at each step
3. SAMC方法的识别结果与检验结果
3.1 识别结果
采用学习样本集的资料,按SAMC的步骤进行计算,即可得到识别结果;并用同一样本集进行检验,以分析所得结果的识别率,从而得到C检验结果.
为了讨论分类特征量对SAMC的影响,我们先用SAMC对学习样本集中3个特征量进行识别,然后再增加识别效果较差的APmax/tme和ASmax/tme,对5个分类特征量的样本进行识别,并对二者进行对比分析. 首先去掉识别率较差的后两个特征,只对前3个特征用SAMC作C检验,结果列于表 2; 然后再对5个分类特征量(包括较差的两个特征量)用SMAC做C检验,结果列于表 3.
表 2 3个分类特征量的C检验结果Table 2. Results of C-test on learning sample set with three features 表 3 5个分类特征量的C检验结果Table 3. Results of C-test on learning sample set with five features
表 3 5个分类特征量的C检验结果Table 3. Results of C-test on learning sample set with five features
从表 2、 表 3可以看出,SAMC识别地震与爆破的结果比较理想,3个分类特征量的识别率达到了92%. 对比表 2、 表 3可知,增加识别率较差的两个特征后识别率略有降低,但并没有太大的变化,可见SAMC的稳定性较好.
3.2 U检验结果
根据学习结果,采用检验样本集进行识别效果的检验,称之为U检验.计算某一个3个特征量测试模板的代价路径分为3步,分别代表某一个测试模板与参考模板的距离. 该3步的顺序为: ① 初动方向; ② P波初至幅值与S波最大幅值比; ③ P波最大幅值与S波最大幅值比. 特征之间是相互独立的,因此,这3步的顺序对结果没有影响.
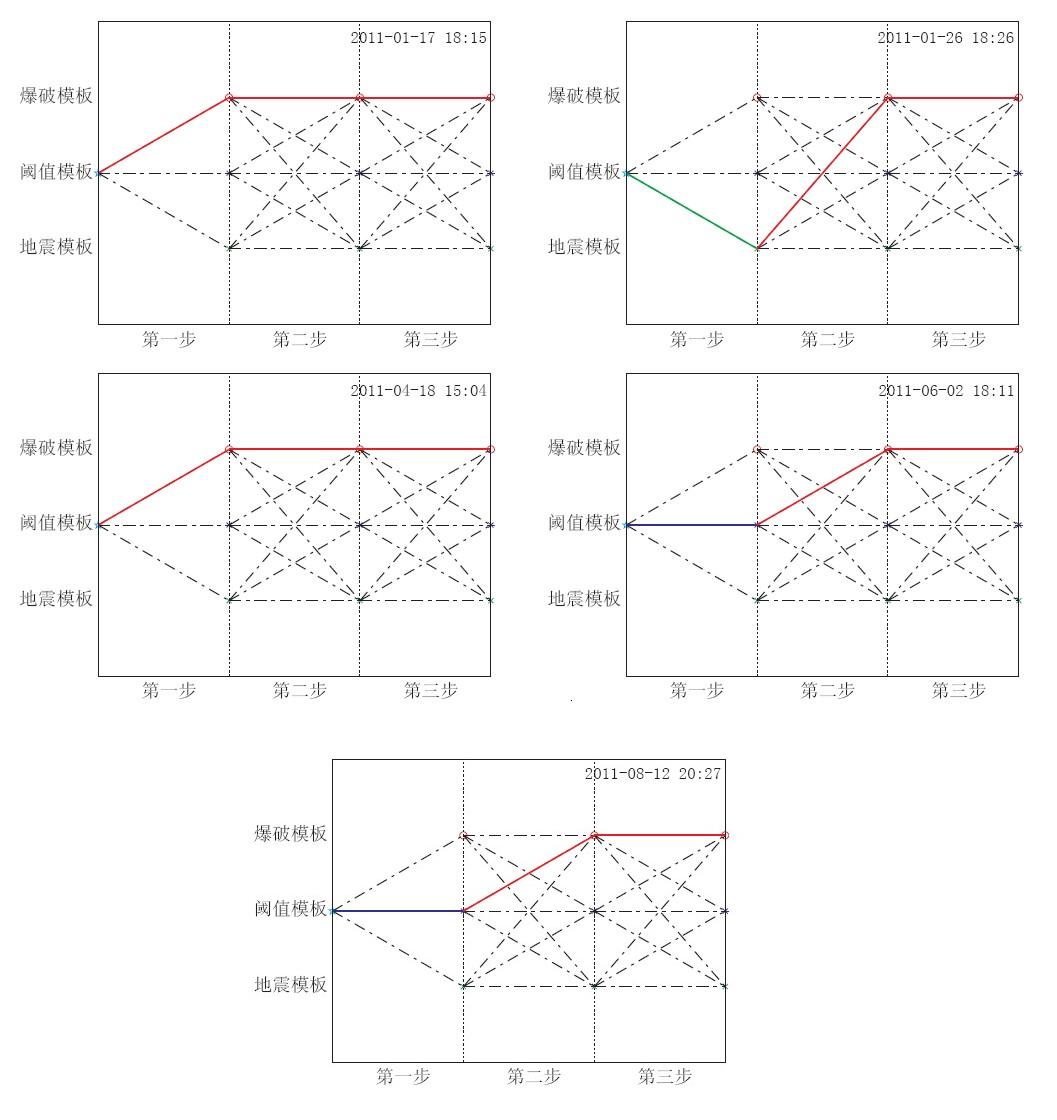
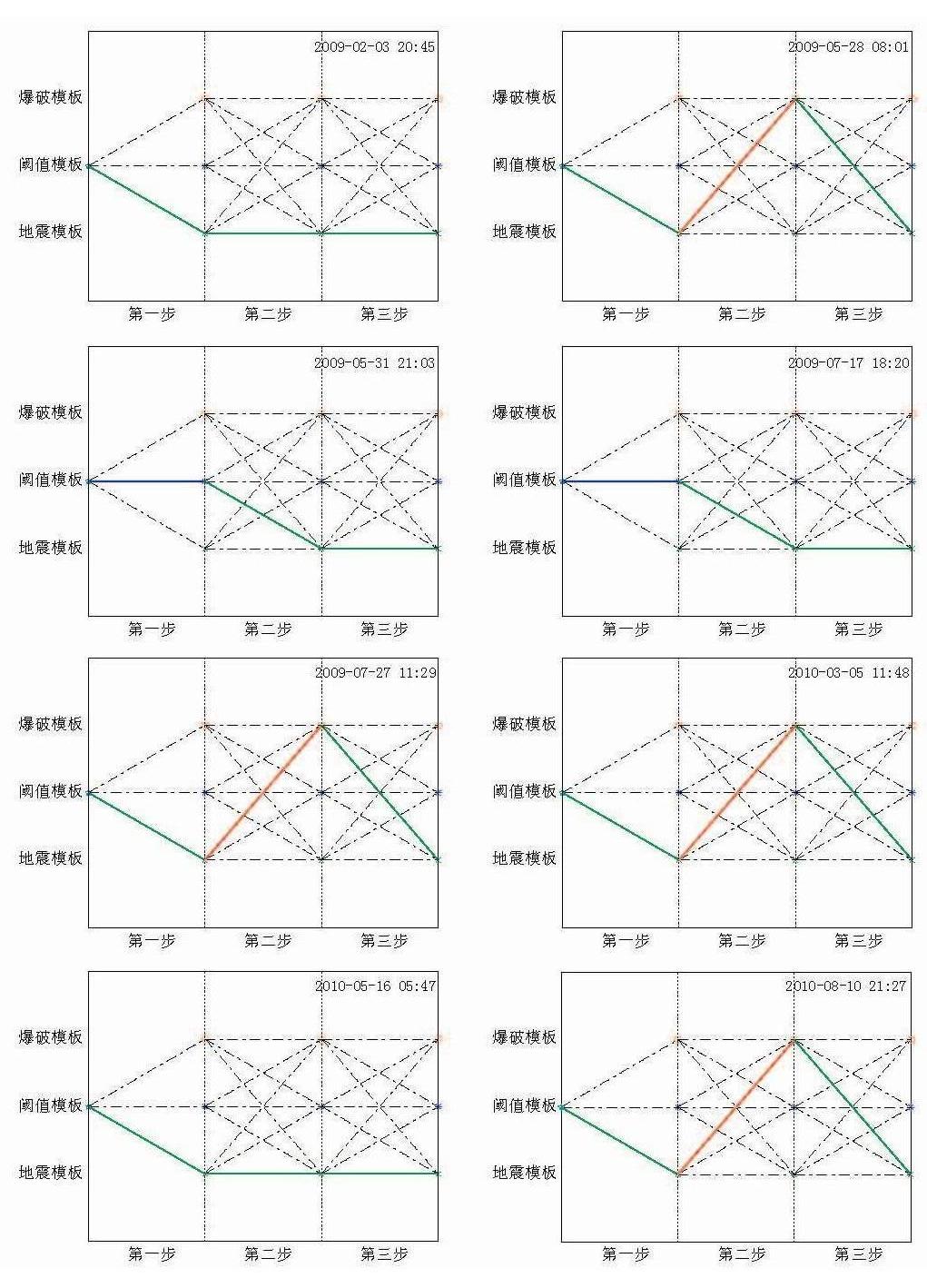
图 3、 图 4分别给出了5次爆破、 8次地震的3个分类特征量的测试模板的全程最优路径.
从图 3描述的情况来看,属于爆破性质的测试模板的特征中,仅有2011年1月26日事件第一步倾向错误,即该事件的初动方向向下与爆破事件初动方向向上相违背; 第二、 第三步全部识别正确,即权重较大的 AP1/ASmax和APmax/ASmax全部识别正确. 仅从图 3来看,很容易得出这5次事件应该被识别为爆破.
图 4中,属于地震的测试事件特征中,大部分初动方向和权重最大的P波最大振幅与S波最大振幅比均距离地震较近,这也决定了这些测试事件会被识别为地震.
上述所列的测试模板代价路径中,每一步的倾向都会体现在最终的全程代价函数值上,全程代价函数值主要表征了该测试事件的各特征综合检验效果. 对于一个测试事件而言,全程代价函数值越接近于-1,表明特征倾向于地震的步骤越多,其识别为地震事件的可信度亦越大; 其全程代价函数值越接近于1,特征倾向于爆破的步骤越多,其识别为爆破事件的可信度亦越大. 为了验证SAMC算法对于掺入识别率较差的特征后的稳定性,表 4列出了检验样本集13个测试事件的3个分类特征量和5个分特征量的U检验结果.
表 4 测试事件的U检验结果Table 4. Results of U-test on all test sample set
从表 4的检验结果来看,3个分类特征量测试模板的识别率达到100%,5个分类特征量测试模板仅有一个识别错误,总的识别率为92%. 可以看出,SAMC方法对测试模板的3个分类特征量U检验结果比较理想,掺入识别率较差的特征后,总体的识别率没有太大变化,说明SAMC的稳定性比较好.
4. 讨论与结论
受动态时间规整法启发,本文提出了一种新的识别天然地震与人工爆破的决策方法SAMC. 该算法通过定义某种代价函数实现路径最优化,求得全程代价函数后,从全程代价函数出发来区分地震与爆破.
在北京及其周边地区选取62次已知类别的事件作为学习样本,另随机选取13次事件作为测试样本. 提取可用于识别爆破与地震的5个特征: 初动方向,P波初至幅值与S波最大幅值比,P波最大幅值与S波最大幅值比,P波最大幅值与尾波持续时间比,以及 S波最大幅值与尾波持续时间比,并提取测试模板和参考模板. 采用SAMC方法对研究区的62次事件(学习样本集)进行学习,识别结果(即C检验结果)显示3个分类特征量识别率达到92%,掺入单特征识别效果较差的两种幅值与持续时间比特征后,5个分类特征量的识别率为90%. 另外选择研究区13次事件(检验样本集)进行U检验,3个分类特征量测试模板的识别率达到100%,5个分类特征量的识别率为92%. 表明SAMC方法可应用于天然地震与人工爆破的识别.
综上,本文提出的SAMC方法具有: ① 代价函数值可以很好地反映该特征的倾向; ② 该算法对识别率较差的特征具有一定的“容忍度”,稳定性较好; ③ 全程代价函数的计算较为简便,而且它的绝对值可以评判事件识别结果的可信度.
-
图 2 人工爆破与天然地震识别量的阈值分析
(a) P波初动方向; (b) AP1/ASmax ; (c) APmax/ASmax; (d) APmax/tme; (e) ASmax/tme 红色圆圈和叉号分别表示学习样本集中的爆破与地震事件; 正方形和棱形分别表示学习样本集中爆破与 地震各项特征的重心; 蓝色圆圈和六角星表示检验样本集中的爆破与地震事件
Figure 2. Thresholds for discriminating the explosions and earthquakes
(a) P-wave first motion; (b) The ratio of P-wave first motion amplitude to the maximum amplitude of S-wave; (c) P/S maximum amplitude ratios; (d) The ratio of P-wave maximum amplitude to duration; (d) The ratio of S-wave maximum amplitude to their duration. The red circles and crosses represent explosions and earthquakes for learning, respectively; the squares and the diamonds represent template of each feature belonging to explosions and earthquakes, respectively; the blue circles and the hexagrams separately represent explosions and earthquakes for testing
表 1 每一步权重值σ
Table 1 Weight σ at each step

表 2 3个分类特征量的C检验结果
Table 2 Results of C-test on learning sample set with three features

表 3 5个分类特征量的C检验结果
Table 3 Results of C-test on learning sample set with five features

表 4 测试事件的U检验结果
Table 4 Results of U-test on all test sample set

-
毕明霞, 黄汉明, 边银菊, 李锐, 陈银燕, 赵静. 2011. 天然地震与人工爆破波形信号HHT特征提取和SVM识别研究[J]. 地球物理学进展, 26(4): 1157-1164. Bi M X, Huang H M, Bian Y J, Li R, Chen Y Y, Zhao J. 2011. A study on seismic signal HHT features extraction and SVM recognition of earthquake and explosion[J]. Progress in Geophysics, 26(4): 1157-1164 (in Chinese).
边银菊, 邹立晔. 2002. 学习向量化(LVQ)在地震和爆破识别中的应用[J]. 地震地磁观测与研究, 23(1): 10-15. Bian Y J, Zou L Y. 2002. Application of learning vector quantization (LVQ) to discriminating earthquakes and explosions[J]. Seismological and Geomagnetic Observation and Research, 23(1): 10-15 (in Chinese).
边银菊. 2002. 遗传BP网络在地震和爆破识别中的应用[J]. 地震学报, 24(3): 516-524. Bian Y J. 2002. Application of genetic BP network to discriminating earthquakes and explosions[J]. Acta Seismologica Sinica, 24(3): 516-524 (in Chinese).
边银菊. 2005. Fisher方法在震级比mb/MS判据识别爆炸中的应用研究[J]. 地震学报, 27(4): 414-422. Bian Y J. 2005. Application of Fisher method to discriminating earthquakes and explosions using criterion mb/MS[J]. Acta Seismologica Sinica, 27(4): 414-422 (in Chinese).
边银菊, 王婷婷, 郭永霞. 2012. 用决策方法识别地震与爆破[J]. 地震学报, 34(3): 397-407. Bian Y J, Wang T T, Guo Y X. 2012. Discrimination between earthquakes and explosions based on decision-making algorithm[J]. Acta Seismologica Sinica, 34(3): 397-407 (in Chinese).
韩绍卿, 李夕海, 安跃文, 刘代志. 2010. 核爆、 化爆、 地震识别研究综述[J]. 地球物理进展, 25(4): 1206-1218. Han S Q, Li X H, An Y W, Liu D Z. 2010. A review on the identification of nuclear explosions, chemical explosions and natural earthquakes[J]. Progress in Geophysics, 25(4): 1206-1218 (in Chinese).
黄汉明, 边银菊, 卢世军, 李锐, 蒋正锋. 2010. ν-SVC算法在地震与爆破识别及窗长度选取中的应用[J]. 地震地磁观测与研究, 31(3): 24-31. Huang H M, Bian Y J, Lu S J, Li R, Jiang Z F. 2010. ν-SVC algorithm applied in earthquake and explosion recognition and the choice of window length[J]. Seismological and Geomagnetic Observation and Research, 31(3): 24-31 (in Chinese).
李夕海, 刘刚, 刘代志, 秦庆强. 2009. 基于最近邻支撑向量特征线融合算法的核爆地震识别[J]. 地球物理学报, 52(7): 1816-1824. Li X H, Liu G, Liu D Z, Qin Q Q. 2009. Discrimination of nuclear explosions and earthquakes using the support vector feature line fusion classification algorithm[J]. Chinese Journal of Geophysics, 52(7): 1816-1824 (in Chinese).
王婷婷, 边银菊. 2011. 识别天然地震和人工爆破的判据选择[J]. 地震地磁观测与研究, 32(6): 62-67. Wang T T, Bian Y J. 2011. Criterion selection of earthquake and explosion recognition[J]. Seismological and Geomagnetic Observation and Research, 32(6): 62-67 (in Chinese).
Bellman R E. 1957. Dynamic Programming[M]. New Jersey: Princeton University Press: 83-86.
Kuyuk H S, Yildirim E, Dogan E, Horasan G. 2011. An unsupervised learning algorithm: Application to the discrimination of seismic events and quarry blasts in the vicinity of Istanbul[J]. Nat Hazards Earth Syst Sci, 11(1): 93-100.
Sammis C G, Biegel R L, Rosakis A J. 2008. An experimental study of S wave generation by fracture damage in underground nuclear explosions[C]//Monitoring Research Review: Ground-Based Nuclear Explosion Monitoring Technologies. California: University of Southern California and California Institute of Technology. 1: 666-671.
Theodoridis S, Koutroumbas K. 2009. Pattern Recognition[M]. London: Academic Press: 482-486.
Taylor S R. 2011. Statistical discriminants from two-dimensional grids of regional P/S spectral ratios[J]. Bull Seismol Soc Am, 101(4): 1584-1589.
-
期刊类型引用(9)
1. 张帆,杨晓忠,王树波. 基于LSTM神经网络的地震事件分类. 计算机应用与软件. 2023(04): 75-79 .  百度学术
百度学术
2. 孟娟,张家声,李亚南. 基于改进EWT和LogitBoost集成分类器的地震事件分类识别算法. 地震工程学报. 2022(05): 1233-1242 .  百度学术
百度学术
3. 周少辉,蒋海昆,曲均浩,李健,郭宗斌,郑旭. 爆破、塌陷识别研究进展综述. 中国地震. 2021(02): 508-522 .  百度学术
百度学术
4. 张帆,杨晓忠,吴立飞,韩晓明,王树波. 基于短时傅里叶变换和卷积神经网络的地震事件分类. 地震学报. 2021(04): 463-473+533 .  本站查看
本站查看
5. 毛世榕,史水平,苏梅艳,蒋志峰,玉壮基. 基于RBF神经网络的地震与爆破识别技术. 地震地磁观测与研究. 2020(03): 59-66 .  百度学术
百度学术
6. 陈润航,黄汉明,施佳朋,薛思敏,袁雪梅. 天然地震与人工爆破地震波形的实时分类研究. 地球物理学进展. 2019(05): 1721-1727 .  百度学术
百度学术
7. 陈润航,黄汉明,柴慧敏. 地震和爆破事件源波形信号的卷积神经网络分类研究. 地球物理学进展. 2018(04): 1331-1338 .  百度学术
百度学术
8. 何浩祥,解鑫,王文涛. 基于动态时间归整距的地震动特性分析及合成精度评价. 振动与冲击. 2018(12): 207-215 .  百度学术
百度学术
9. 赵刚,黄汉明,卢欣欣,郭世豪,柴慧敏. 基于BP-Adaboost方法的天然地震和人工爆炸事件波形信号分类识别研究. 地震工程学报. 2017(03): 557-563 .  百度学术
百度学术
其他类型引用(9)




 下载:
下载: