引言

地球表层时刻存在的微弱振动被称为地脉动或微动(microtremors)，在天然地震学研究中将其称为背景噪声． 地脉动的震源复杂多样，通常被认为是多种震源经地下介质散射而被地震仪器记录到的一种信号． 根据信号的周期成分范围地脉动一般分为两类: 频率高于1 Hz的脉动信号和频率低于1 Hz的长周期信号． 前者主要源于人类活动诸如交通工具、 工厂机器运转等，由于高频信号在地球传播过程中衰减得较快，所以地脉动中的高频成分主要源于近距离源； 后者主要源于自然因素诸如风、 河水流动、 海洋波浪等，由于其在传播过程中衰减得较慢，因此长周期记录中可能含有更大范围的介质信息． 目前长周期微动信号主要应用于利用互相关技术提取经验格林函数进行壳幔结构的层析成像研究(Yao et al，2006; Yang et al，2007)； 在工程应用和浅层勘探领域，空间自相关(spatial autocorrelation，简写为SPAC)方法应用更为广泛，例如，何海兵等(2010)利用微动的SPAC方法结合地震勘探中的剥层反演法得到了场地不同深度的S波速度结构． 此外，该方法在地热探查(Xu et al，2012)、 “孤石”探查(徐佩芬等，2012)及隐伏断裂探测(范小平等，2015)等方面均得到了成功应用．

在工程地震领域，利用微动探测地层S波速度结构的经济、 快速、 高效性也引起了众多研究人员的重视． 姚运生和付少兰(2000)及陶夏新等(2001)简述了地脉动方法的基本原理，指出了微动勘探为工程建设服务的前景； 陶夏新等(2002)与日本同行合作开展了地脉动联合观测，获得了一系列有价值的试验数据，基于这些数据，师黎静等(2006)深入分析了采用空间自相关方法获得的S波速度结构在场地反应分析计算中的应用效果； 董连成等(2009)利用遗传算法和单纯形法通过反演提取瑞雷波和勒夫波的频散曲线，得到了试验场地的S波速度并进行了分析． 这些研究均显示出微动方法在工程地震学中有着巨大的前景．

空间自相关方法最早由Aki(1957，1965)提出，之后得到一系列改进． 在台阵布置方面，正三角型或嵌套三角型的布设方式应用最为普遍(何正勤等，2007; Xu et al，2012; 徐佩芬等，2013)． 为了使该方法适应更多工况条件，还发展了扩展空间自相关法(extensible spatial autocorrelation，简写为ESAC)(张维等，2013). Asten(2006)使用的正六边型布台法更适用于入射角方位比较集中的情况； 对于满足噪声源均匀分布的地区，利用双台空间自相关方法也能获得好的勘探效果(Hayashi et al，2013)．

自相关系数计算方法方面，罗松和罗银河(2014)总结了目前已有的自相关系数计算方法，并通过数值模拟对比了各种计算方法的效果，其结果指出对于窄带滤波法，不加时窗法和加时窗法的结果均与理论空间自相关系数一致； 而对于快速傅里叶法，加时窗法的计算结果与理论空间自相关系数一致，其不加时窗法的结果与降幅的理论空间自相关系数一致. 在误差控制方面，Asten(2006)，Claprood和Asten(2010)以及文成哲等(2010)从不同角度进行了较为详细的讨论和研究． 近期一些理论研究还表明空间自相关方法与背景噪声互相关方法具有一致性(Yokoi，Margaryan，2008; Tsai，Moschetti，2010); 另外，Haney等(2012)尝试将微动方法的应用扩展到三分量记录的计算中，并且取得了较好的效果．

本文首先简要介绍了空间自相关方法的基本原理； 然后针对一个小型圆形排列台阵，利用多种台站对组合以多组方位平均的方式进行空间自相关系数计算并提取频散曲线，指出利用几个特殊点来约束自相关系数与贝塞尔函数拟合的方法提取频散曲线的可行性； 最后根据所提取的瑞雷波频散曲线反演该场地的S波速度结构，并与钻孔结果进行比较，以判断空间自相关法在浅层探测应用中的效果．

1.   理论与方法

空间自相关(SPAC)方法是基于微动信号在时间和空间上平稳随机分布这一假设. 在该假设条件下，对于相距为r的两个点的微动记录作空间相关运算. Aki(1957)给出了方位平均后的空间自相关函数可以用零阶贝塞尔函数来表示，即

式中，r为两台站间的距离，f为频率，c(f)为瑞雷波相速度，ρ为方位平均后的自相关系数，J₀为第一类零阶贝塞尔函数． 该式适用于基阶面波能量为主，利用垂向记录分量进行空间自相关提取瑞雷面波频散的情形．

空间自相关系数的计算大致分为时域(或称窄带滤波法)和频域两大类. 时域空间自相关系数求取(Aki，1957)的步骤为： ① 选取记录良好的原始记录，对每段选取的记录平均分成若干段，分段时要保证可以覆盖足够多的频率信息； ② 对数据进行不同中心频率的窄带滤波处理，通过式(2)描述的过程得到以滤波器中心频率为自变量的近似单色波记录； ③ 对单频记录的距离为r的台站对按式(3)计算空间自相关系数，并将相同台站对的结果进行平均； ④ 循环第②和第③步，计算出一系列频率值所对应台站对的空间自相关系数，对所得的空间自相关系数按式(4)两两取方位平均，得到用于计算频散的平均自相关系数．

式中，u(t)表示微动记录的时间序列，P(f₀)表示中心频率为f₀的窄带滤波器，u(t，f₀)表示经过窄带滤波后的单频微动信号，u₀表示台站对的参考位置，u_i表示不同位置的信号，ρ_i(r，f₀)表示距离为r、 中心频率为f₀的第i个台站对的空间自相关系数，〈·〉表示整体平均，Avg表示算术平均．

平面上圆形排列台阵中各台站的位置一般用极坐标形式表示. 以参考点为圆心，θ为台站方位角，空间自相关系数的频率域计算公式为

式中： S(r，θ，f)为参考点记录与其它记录点的互功率谱，S₀(0，f)和S_r(r，f)分别表示参考点和与其距离为r的另一点记录的自功率谱； Re表示取实部，确保空间自相关系数为实数. 实际上也有研究人员将不取实部所得的空间自相关系数称为复相关系数，例如Asten(2006)曾讨论过复相关系数的虚部可以表示空间自相关系数的误差．

频域计算相对于时域计算的优势是去掉了多次窄带滤波过程，只利用一次傅里叶变换后完全在频率域内进行计算，因此大大加快了运算速度． 频域空间自相关系数求取的步骤为： ① 选取良好的记录数据，将数据分段； ② 将分段后的数据进行傅里叶变换得到频率域数据，在频率域内分别计算对应数据段的自功率谱和互功率谱，然后将各段数据结果进行平均； ③ 将平均后的自功率谱和交叉谱结果代入式(5)计算方位平均，便可得到方位平均的空间自相关系数．

2.   数据采集与频散曲线提取

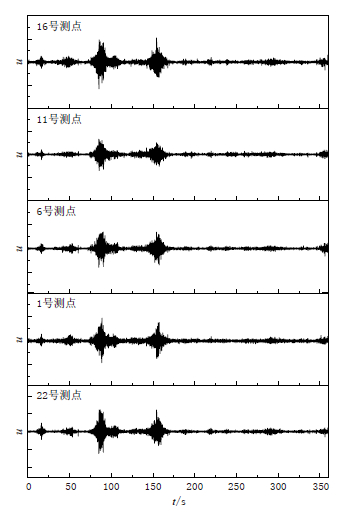
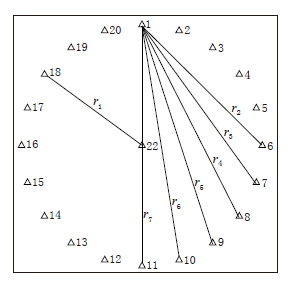
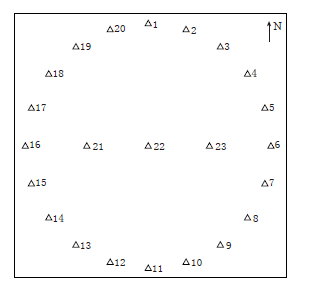
2012年，我们在云南省玉溪市某地进行微动探测试验，传感器布置采用如图 1所示的圆形台阵． 该台阵外围圆形排列的直径为16 m，圆周上检波器由正北沿顺时针方向标号分别为1—20号； 在圆形台阵中间沿东西方向的直径上以4 m的等间距布置21号，22号和23号，即22号检波器位于圆形排列的圆心处． 采用4.5 Hz的垂向单分量检波器，利用该台阵以125 Hz的采样率共记录了10组长度为6分钟的微动(背景噪声)． 图 2给出了某次记录中的5条微动记录，分别为图 1中22号，1号，6号，11号和16号测点位置的记录．

图  1  试验台阵布置

Figure  1.  Array layout of the experiment

下载: 全尺寸图片 幻灯片

图  2  原始微动记录

Figure  2.  Raw records of the original microtremors

下载: 全尺寸图片 幻灯片

本文中空间自相关系数的计算采用频率域计算方式，在试验自相关系数计算时对台站对的选取并不仅限于传统的圆心点与圆周点的组合. 受Roberts和Asten(2004)正六边型台阵求取不同组合方位平均自相关系数的启发，只要间距相同的台站对能在各方位均匀分布即可获得方位平均的空间自相关系数，因此选取圆周各点组成均匀分布的一系列台站对，用于计算方位平均的空间自相关系数，考虑射线路径则要尽可能覆盖勘探区域. 本文求取了7组不同台站间距的方位平均自相关系数，典型台站对的射线分布如图 3所示，所有台站对分组列于表 1．

图  3  7组典型台站对组合示意图

Figure  3.  Schematic diagram of seven typical station-pairs

下载: 全尺寸图片 幻灯片

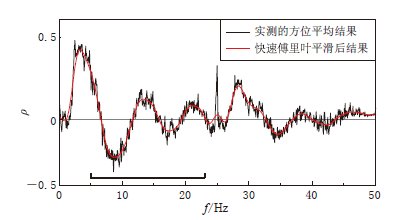
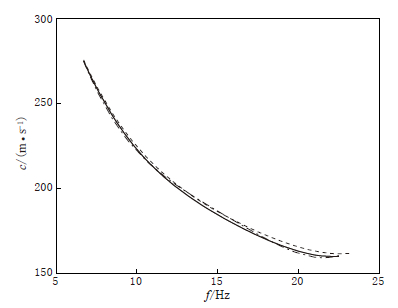
表  1  空间自相关系数计算台站对分组

Table  1.  Station-pairs with different distance used for calculation of SPAC coefficients

	r1=8 m	r2=11.31 m	r3=12.94 m	r4=14.26 m	r5=15.22 m	r6=15.80 m	r7=16 m
台站对组合	1-22	1-6	1-7	1-8	1-9	1-10
	2-22	2-7	2-8	2-9	2-10	2-11
							1-11
	15-22	15-20	14-20	13-20	12-20	11-20	2-12
	16-22	16-1	15-1	14-1	13-1	11-1	
	17-22	17-2	16-2	15-2	14-2	11-2	10-20
						
	20-22	20-5	20-6	20-7	20-8	20-9
注： 表中数字代表测点编号.

下载: 导出CSV 

| 显示表格

对于单个台站对的自相关系数计算，取分段窗口长度为1000个记录点，即时长为8 s，当前窗口与前一窗口有250个采样点叠加，对所有窗口计算的相关系数进行叠加得到单个台站对最终的空间自相关系数． 单个台站对计算出的空间自相关系数与相同半径的结果作全圆周的方位平均即可得到一条空间自相关系数曲线. 例如，图 4中黑色实线为台站对间距为16 m经过方位平均后的实测空间自相关系数曲线，利用快速傅里叶曲线平滑方法(Savitzky，Golay，1964; Press et al，1992)将其作平滑处理，结果如图 4中红色实线所示． 同理，可得其它不同间距台站对经平滑后的空间系自相关系数曲线．

图  4  间距为16 m的台站对的空间自相关系数ρ

Figure  4.  The SPAC coefficient ρ of the station-pairs with interval distance of 16 m

下载: 全尺寸图片 幻灯片

得到自相关系数后，可以根据式(1)来提取频散曲线． 由式(1)可以看出，当r为定值时，ρ(r，f)则为频率的函数(图 4)，此时先判断可分辨频段范围; 该范围的选取主要根据空间自相关系数曲线与贝塞尔曲线相似的部分来判断，多依赖人工经验判断． 据此方法本次试验可分辨的频段范围大约为5—23 Hz，如图 4中黑色粗线段所示． 图 5给出了不同间距台站对的空间自相关系数曲线在有效频段的结果．

图  5  不同间距台站对在有效频段内的=空间自相关系数ρ

Figure  5.  The SPAC coefficients ρ in effective frequ-ency band for station-pairs with different distance

下载: 全尺寸图片 幻灯片

将有效频段的空间自相关系数与标准贝塞尔曲线的对应段进行拟合，即可获得该频段的频散曲线． 若要严格地进行观测曲线与模型曲线的匹配，则利用式(6)进行计算，然后选取最小方差值所对应的J₀(f)频散曲线作为频散提取结果.

式中，Var为观测自相关系数曲线与模型频散曲线的方差，f∈[f₁，f₂]为空间自相关系数的可用频率范围，ρ(f)为空间自相关系数，J₀(f)为模型频散曲线值计算的零阶贝塞尔函数．

在等间距r的条件下判断ρ(f)与J₀[2πfr/c(f)]的拟合比较困难，这主要源于零阶贝塞尔函数项J₀[2πfr/c(f)]，从其形式可以看出，贝塞尔函数值的自变量由f和c(f)决定，二者的对应关系即频散曲线为待求结果． 对ρ(f)与 J₀[2(fr/c(f)]作拟合，则需要将一系列频率值与一系列相速度值相组合形成模型频散曲线来多次重复试算，并代入式(6)进行最小二乘拟合． 为此，本文利用与Aki(1957)一文中类似的频散曲线提取方法，暂称其为特殊点约束法． 这里所用的特殊点不只是一条空间自相关系数曲线的极大值点、 零点和极小值点，而是用了7条不同r值的空间自相关系数曲线上的点，这样可以找到更多的点来约束频散曲线． 其计算步骤为： ① 找出零阶贝塞尔函数的零点、 极大值点和极小值点的自变量值，记为x； ② 找出不同台站对间距方位平均的空间自相关系数零点和极大值点及极小值点所对应的台站对间距r和频率f； ③ 因为式(1)成立，所以

成立，将x，r，f代入式(7)即可得到不同频点的面波相速度c(f)．

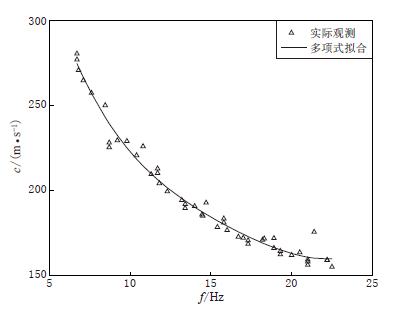
图 6给出了实际观测的频散曲线及其多项式拟合，其中三角形为将不同空间自相关系数曲线所对应的特殊点代入式(7)得到的频散点，其计算数据如表 2所示． 将这些频散点利用多项式拟合方法(宗殿瑞等，1998)即可得到相应的频散曲线，如图 6中实线所示． 同时，将实测频散点与拟合频散曲线的残差当作一种表示误差的参数，作为频散曲线反演时的输入参数．

图  6  实际观测的频散点及其多项式拟合

Figure  6.  The observed dispersion points (triangles) and its polynomial fitting curve

下载: 全尺寸图片 幻灯片

表  2  空间自相关系数曲线的特殊点取值

Table  2.  The special points of SPAC coefficients

特殊点	x	f/Hz
		r1=8 m	r2=11.31 m	r3=12.94 m	r4=14.26 m	r5=15.22 m	r6=15.80 m	r7=16 m
零点	2.40	10.8	8.45	7.6	7.1	6.8	6.7	6.7
极小值点	3.83	14.5	11.3	10.4	9.8	9.2	8.9	8.7
零点	5.52	18.9	14.5	13.2	12.3	11.8	11.7	11.7
极大值点	7.01	22.2	17.0	15.4	14.5	14.0	13.5	13.4
零点	8.65		21.4	18.2	16.7	16.0	15.8	15.8
极小值点	10.18			20.5	18.9	18.3	17.7	17.3
零点	11.79			22.5	21.0	20.0	19.5	19.3
极大值点	13.33					22.2	21.4	21.0

下载: 导出CSV 

| 显示表格

在频率值固定的情况下，式(1)中的ρ(r，f)变成关于r的单值函数，等号右侧的J₀项则仅与r/c(f)相关，故可通过迭代c(f)的值来拟合ρ(r，f)与J₀[2πfr/c(f)]，在可分辨频段两者拟合最好时的c(f)即为该固定频率下的面波相速度．

为了求取空间自相关系数第一个零点以前的频散值，作者曾尝试应用该方法以期得到更低频段的频散曲线． 在此过程中，发现由于r值只处于8—16 m的范围内，ρ(r，f)-r曲线不能形成对贝塞尔曲线形态的约束． 对比曾运用该方法提取频散曲线的文献(Hayashi et al，2013； 徐佩芬等，2013)，我们发现r值的离散性较大，ρ(r，f)-r曲线与贝塞尔曲线很类似，可获得较好的约束． 因此，这种固定频率迭代计算相速度的方法，适用于台站对间距离散性较大且能够形成良好曲线形态的情形． 最终本文仅得到6.7—23 Hz范围的频散曲线． 图 7展示了从10组微动记录中随机选取的3组数据所提取的频散曲线. 可以看出，利用特殊点约束方法所提取的频散曲线形态非常相似，说明该方法在提取频散曲线方面的稳定性很好．

图  7  从随机选取的3组微动数据中所提取的频散曲线

Figure  7.  The observed dispersion curves extracted from three groups of measurements

下载: 全尺寸图片 幻灯片

3.   剪切波速度反演与解释

如图 7所示，本文随机选取的几组数据的频散曲线非常接近，因此本文仅选取其中一条频散曲线进行本场地S波速度结构的反演． Xia等(1999)的研究已表明面波频散是S波速度、 P波速度、 密度及层厚度的函数，而瑞雷波速度频散对S波速度最为敏感，P波速度和密度对面波频散影响较小则一般不予考虑，因此本文对面波的反演结果仅给出地层的S波速度结构． S波速度结构是进行工程勘察和工程抗震的重要参数，对场地类别划分、 场地卓越周期估计以及场地地震动放大倍数估计等具有重要作用． 因此，面波频散对S波速度结构的敏感性有助于获得场地的动力学参数，为场地评估服务．

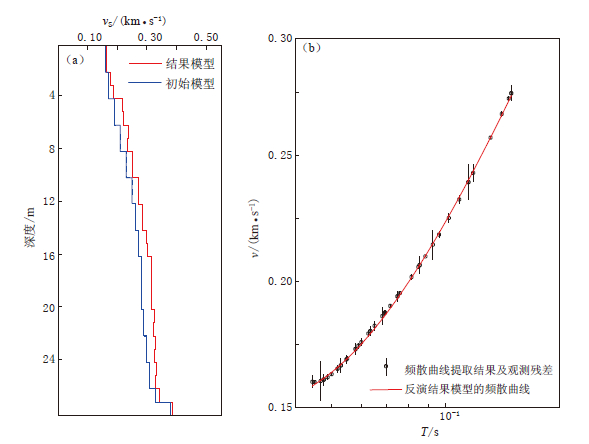
反演的初始模型为根据半波长法建立的随深度递增的S波速度初始模型，由半波长法可以粗略估计本试验频散曲线可探测深度大致为20—25 m，因此本文模型主要划分25 m深度内的地层． 图 8给出了本文利用PROGRAMS.330程序(Herrmann，Ammon，2002)进行反演的结果，其中图 8a为初始模型(蓝色实线)和结果模型(红色实线)，图 8b为瑞雷面波频散曲线．

图  8  初始模型和反演结果模型(a)及相应的观测频散曲线和反演模型的频散曲线(b)

Figure  8.  The initial (blue line) and inverted (red line) model (a) as well as observed (circles) and predicted (red line) dispersion curves (b)

下载: 全尺寸图片 幻灯片

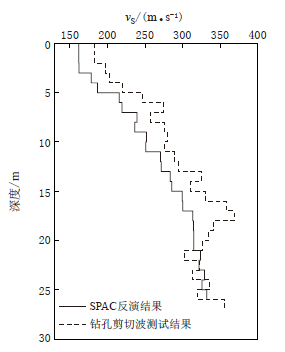
图 9给出了本文利用空间自相关方法得到的浅层剪切波速结构与单孔法直接测试得到的实测结果的对比. 可以看出，20 m深度以内二者吻合度较高，速度变化趋势一致，但是空间自相关方法反演的波速总是稍低于单孔测试得到的波速值，二者的速度差值基本小于10%．

图  9  反演得到的剪切波速结构与钻孔结果的对比

Figure  9.  The shear wave velocity struc-ture from inversion (solid line) and drilling test (dashed line)

下载: 全尺寸图片 幻灯片

4.   讨论与结论

本文利用空间自相关(SPAC)方法从玉溪圆形小型排列的微动记录中提取了瑞雷面波频散曲线． 在频散提取过程中使用了新颖的台站对组合方式. 这种台站对组合方式是一种优化组合，大大扩展了仅利用圆心点与圆周点组成台站对的传统方式，从而扩展了信息的获取量． 之后利用特殊点约束法提取频散曲线，结果表明该方法简单易行，所提取的频散曲线结果稳定，适合小型排列微动数据的处理．

通过对空间自相关方法提取的频散曲线进行反演，给出了场地浅层的S波速度结构，其与钻孔测试结果非常相近，说明空间自相关方法可以为场地调查提供有效资料. 与主动源面波勘探相比，本文方法不用激发，可以大大减小劳动量，减少噪音，应用优势较为明显．

本文在数据处理时，特殊点为人工选取，该方法的自动实现将会进一步提高效率． 另外，Roberts和Asten(2004)的研究在反演时直接利用正演的空间自相关系数与观测的空间自相关系数进行拟合来控制反演结果，省略了观测曲线提取频散的过程，这种直接反演法的效率更高，但是由于反演问题有很多不确定性，模型在先验信息不足的情况下需要选取优秀的全局优化算法进行计算． 利用这种方法，需要作大量的工作将面波正演、 反演方法与空间自相关结果进行融合，这将在我们今后的研究中给出． 本文仅就空间自相关方法对瑞雷波竖向分量进行频散曲线提取，对于勒夫波及瑞雷波径向分量提取频散曲线可能能够对勘探结果进行更好的约束，这也是未来的重要研究方向．