Phase correlation features of geoelectric field diurnal waveforms in multi-orientation
-
摘要: 本文以电磁环境、装置系统、日变波形均具有代表性的海安、平凉、瓜州等7个台站为对象，基于大地电场潮汐机理和裂隙水(电荷)渗流(移动)模型，应用快速傅里叶变换和矢量分析方法，研究这7个台站在2009—2015年多个时段、多个测向的地电场日变波形的相位关系及影响因素.结果显示：多方位地电场观测的日变波形之间具有同相或反相的相位关联特征; 当观测地电场的电极与仪器的连接方式确定后，不同测向地电场日变波形的相位关联即由场地岩体裂隙优势方位所决定，且这种相位关联特征具有相对稳定性.Abstract: In general, recognizable diurnal variation waveforms appear at 70 percent of the more than one hundred geoelectric field stations in Chinese mainland. In this paper, we discussed seven stations including Hai'an, Pingliang, Guazhou, which are representatively characterized by the electromagnetic environment, device system and the diurnal waveforms. Based on the tidal mechanism and the model of rock crack water seepage or the electric charges movement in crack water, and with the application of fast Fourier transform algorithm and vector analysis methods, we studied the phase correlation and influence factors of diurnal waveforms of the seven stations in multiple periods and multi-orientation during 2009—2015, and received the following conclusions: geoelectric field diurnal waveforms observed in each orientation always show the same or opposite phase correlation; the dominant orientation of rock crack will decide phase correlations among geoelectric field diurnal waveforms observed from multi-orientation when the connection mode between electrodes and the instrument is determined, and the correlations are relatively steady.
-
引言
本文提出了一个模型试验来验证Zheng和Psencík(2002)给出的反演公式． 与Gaiser(1990)和Horne等(1998)使用的方法相比，本试验更具有普遍意义． 在实验中，使用多震源垂向地震剖面(vertical seismic profile,简写为VSP)数据反演介质的局部各向异性参数，三分量地震记录数据不受自由界面的影响． 所研究的介质是一种垂向非均匀弱各向异性介质，具有任意的对称性． 对于这样的各向异性介质，我们寻找一种参考各向同性介质，各向异性介质与参考各向同性介质略有不同． 偏振矢量可以很直接地从三分量地震图中得到，然而，慢度矢量的确定却比较复杂． 在此，我们使用Gaiser(1990)提出的方法，钻孔中慢度矢量的垂直分量由在钻孔中记录到的走时确定，因为假设介质是横向均匀的，所以能够利用走时的互易性确定钻孔中慢度矢量的水平分量． 应该指出，Gaiser(1990)仅仅考虑具有垂直对称轴的横向各向同性介质(transversely isotropic media with vertical axis of symmetry，简写为VTI)，慢度矢量总是被限制在有震源和钻孔所决定的垂直平面内，而在我们的模型中介质可以具有任意对称性，慢度矢量可以背离垂直平面． 如果qP波的慢度矢量和偏振矢量是已知的，那么，慢度公式和偏振公式形成一套线性代数方程组，使用这套方程组可以确定钻孔中检波器周围介质的各向异性参数． 我们进一步把垂向非均匀各向异性介质扩展到横向非均匀情况，从慢度公式和偏振公式中消掉慢度矢量的水平分量，得到了适用于仅有一个慢度分量时的反演公式，并用一条实际的VSP观测资料进行验证．
1. 基本方法
使用一个右手笛卡尔坐标系，x轴和y轴在水平面内，z轴垂直向下为正方向． 在弱各向异性(weakly anisotropic，简写为WA)介质中，可以把P波的慢度c-1和偏振矢量gi表示为(Zheng,Psencík,2002; Zheng,2004; 郑需要等,2010)
式(1)和式(2)中，pk是WA介质中的慢度矢量; pkpk=c-2； 矢量e(1)i，e(2)i，ni=e(3)i分别为定义在接收点的各向同性介质中沿P波射线的3个相互垂直的单位矢量； α和β分别为各向同性介质中的P波和S波的速度； 矢量ni是射线的切线方向； 单位矢量e(1)i和e(2)i可以在垂直于ni的平面内任意选取． 但下面的选择为公式的推导和计算带来很大的方便(Psencík,Gajewski,1998; Zheng,Psencík,2002)
式中，D=(n21+n22)1/2,n21+n22+n23=1．
在波的传播方向， n =(cosφsinθ,sinφsinθ,cosθ)，其中， φ是方位角，而θ是波的传播方向与z轴的夹角(0≤φ≤2π,0≤θ≤π)． 所以，D=sinθ，而且 e (1) ,e (2)可写为
为了避免D=0或者非常接近于零的时候式(3)中的分母为零的问题，我们选择使用式(4)．
式(1)和式(2)中的B13,B23和B33被称为弱各向异性矩阵元素，它们是15个WA参数的函数． 这15个WA参数可以完全描述弱各向异性介质中qP波的性质(Psencík,Gajewski,1998; Zheng,Psencík,2002)． 重写式(1)和式(2)，使包含WA参数弱各向异性矩阵元素B13,B23和B33出现在方程的左边，它们是待求解线性方程组中的未知参数
式(5)和式(6)代表由15个WA参数作为未知参数的线性方程组． 方程组等号右端的偏振矢量gk和慢度矢量pk可以从观测中得到． 为方便起见，将式(5)称作慢度公式，式(6)称作偏振公式．
2. 合成数据实验
考虑一个合成的多方位、 多震源VSP实验． 使用右手笛卡尔坐标系，x轴和y轴在水平面内，z轴正方向朝下． 对于钻孔中的每一个接收点，如果知道了偏振矢量和慢度矢量，便可得到3Ns×Np个方程. 其中，Ns为沿一条剖面的震源数目，Np为具有不同方位的剖面数目． 要想由qP波唯一地确定15个各向异性参数，至少需要5条剖面(Psencík,Gajewski,1998)． 模型位于立方体中，其尺度参数为-1.0≤x≤1.0，-1.0≤y≤1.0，-1.0≤z≤1.0(单位： km)． 介质为VTI介质，由下面的两个密度归一化的弹性矩阵说明． 在地表z=0 km处，弹性参数(单位： km2/s2)为
在z=1 km处，弹性参数为
VTI介质的对称轴先绕y轴(离开垂直轴)转动80°,然后再绕x轴转动25°，最后得到的两个矩阵的所有元素都不为零，可以把它们看作是一般的弹性矩阵．
钻孔坐落在坐标系的原点，在钻孔里等间隔地布设13个三分量地震仪，间距为0.05 km，深度为0.1—0.7 km，忽略自由地表效应． 在地表跨过钻井口布设6条剖面，方位(从x轴开始逆时针方向)依次为0°，30°，60°，90°，120°和150°． 在钻孔一边每一条剖面上有9个震源，最近的震源距钻孔0.1 km，相邻震源的距离为0.1 km(图1)． 在这一观测系统中，每一个接收点有108条射线． 使用各向异性介质中的射线追踪方程，可以计算出震源到接收点之间的射线． 在模型的上部，射线覆盖相当好，最浅的接收点不仅被近水平的射线照亮，也被近垂直的射线照亮． 最深的接收点的射线覆盖不如浅部的接收点覆盖得那么好. 它们主要是被近垂直的射线照亮，没有近水平的射线照在这些接收点上． 因此，我们不能期望在深的接收点处得到好的反演结果． “观测的”三分量合成地震图是由修改版的Anray软件包计算得到的(Gajewski,Psencík,1990)．
![]()
图 1 多方位多离源距的VSP实验示意图Figure 1. Schematic diagram of multi-azimuthal and multi-source offset VSP experiment从“观测的”合成地震图上可以获得qP波的到时和偏振矢量． 在每一个接收点，使用到时决定P波的参考速度α，S波的速度为β=α/ 3 ． 利用相邻接收点的到时决定慢度矢量的垂直分量，慢度矢量的径向分量根据走时的互易性决定，切向分量很小而被忽略． 根据每一接收点的参考速度，可以建立背景各向同性模型，它是一个一维垂向非均匀速度模型． 在这个模型里进行射线追踪，可以得到每个接收点处的e(1)i,e(2)i和ni； 也可以用接收点处的偏振矢量近似地确定这些矢量． 后者与上覆介质无关，可以避免复杂的射线追踪． 由此便可得到式(5)和式(6)左边所有的系数和右边的观测值． 因为式(5)和式(6)是线性方程组，可以使用奇异值分解的方法进行求解反演．
基于6条剖面的数据，得到了图2所示的反演结果． 图2a,b,c各选择了3个深度的接收点的反演结果，其深度值依次为0.25，0.45和0.65 km． 在每一个接收点，左边三列给出了精确的对称轴的投影(实线)和反演得到的结果(虚线)； 最右边一列给出了包含对称轴的相速度曲线，水平坐标表示波的传播方向与对称轴的夹角，从0°(对称轴方向)到90°(各向同性面)，垂直坐标表示相速度． 可以看出，反演结果与精确解非常接近，慢度公式与偏振公式的联合反演结果好于使用单一公式的反演结果． 正如所期望的那样，最深的接收点的反演结果不如最浅的接收点的反演结果好，因为最深的接收点没有很好地被射线照亮.
当使用3条剖面时，反演结果如图3所示． 3条剖面的方位角分别为0°,60°和120°． 如前所述，3条剖面少于完全恢复所有各向异性参数所需的剖面的数量(5条)． 可以看出，反演结果与使用6条剖面的结果相比稍差一些，特别是对称轴在(x，y)平面内的投影和相速度的变化形式，然而相速度与真速度的基本特征仍然得以保留． 慢度公式反演结果比较好，联合反演也产生了较好的结果．
![]()
图 2 使用6条剖面资料反演各向异性参数的结果 (a) 由慢度公式(5)反演得到； (b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到． 各子图的上、 中、 下3行对应的接收点深度分别为0.25，0.45和0.65 km． 左边三列给出精确的对称轴投影(实线)和反演结果(虚线)； 最右边一列给出包含对称轴的相速度曲线，水平坐标表示波的传播方向与对称轴的夹角，垂直坐标表示相速度，实线为相速度的准确值，虚线为反演结果Figure 2. Inversion for WA parameters by using data from 6 profiles (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The receiver depths for the upper,middle and lower rows in each plot are 0.25，0.45 and 0.65 km,respectively. The first three frames from the left show the exact (solid line) and inverted (dashed line) projections of axis of symmetry; the frame on the right shows phase velocity sections within the symmetry plane,in which the horizontal coordinate represents angles between wave propagation direction and axis of symmetry,vertical coordinate represents phase velocity,solid line denotes the exact value of phase velocity and dashed line denotes inversed result![]()
图 3 使用3条剖面资料反演各向异性参数的结果． (a) 由慢度公式(5)反演得到； (b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到. 图注说明同图2Figure 3. Inversion for WA parameters by using data from 3 profiles. (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The illustration is the same as for Fig.2下面的结果和图形显示了不同水平的噪声对数据及反演结果的影响． 首先在观测数据 中加入10%的随机噪声． 图4和图5分别显示了使用6条剖面和3条剖面的反演结果． 在图4中反演得到的对称轴与精确的对称轴有一点点偏离，其它的与图2所示结果没有明显差 别． 图5显示噪声对于对称轴在(x，y)平面的投影有较强的影响，反演得到的相速度剖面与精确解仍然比较吻合.
![]()
图 4 使用6条剖面资料、 数据中加入10%随机噪声后的反演结果． (a) 由慢度公式(5)反演得到；(b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到. 图注说明同图2Figure 4. Inversion for WA parameters by using data with 10% random noise from 6 profiles. (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The illustration is the same as for Fig.2![]()
图 5 使用3条剖面资料、 数据中加入10%随机噪声后的反演结果． (a) 由慢度公式(5)反演得到；(b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到. 图注说明同图2Figure 5. Inversion for WA parameters by using data with 10% random noise from 3 profiles. (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The illustration is the same as for Fig.2当观测数据中加入了20%的随机噪声时，从6条剖面得到的反演结果仍然很好(图6)．这种水平的噪声对使用3条剖面的反演结果有一些影响(图7)． 如果噪声水平达到30%，可以看到使用6条剖面的反演结果(图8)和使用3条剖面的反演结果(图9)都与精确解有较大的偏离． 使用慢度公式得到的结果好于使用偏振公式的结果，偏振公式对联合反演也有 较大的影响． 使用6条剖面和慢度公式得到的结果仍然是可以接受的，使用偏振公式和联合反演的结果有非常大的畸变． 进一步增大噪声水平将导致更严重的畸变．
![]()
图 6 使用6条剖面资料、 数据中加入20%随机噪声后的反演结果． (a) 由慢度公式(5)反演得到；(b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到. 图注说明同图2Figure 6. Inversion for WA parameters by using data with 20% random noise from 6 profiles. (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The illustration is the same as for Fig.2![]()
图 7 使用3条剖面资料、 数据中加入20%随机噪声后的反演结果．(a) 由慢度公式(5)反演得到；(b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到. 图注说明同图2Figure 7. Inversion for WA parameters by using data with 20% random noise from 3 profiles. (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The illustration is the same as for Fig.2![]()
图 8 使用6条剖面资料、 数据中加入30%随机噪声后的反演结果．(a) 由慢度公式(5)反演得到；(b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到. 图注说明同图2Figure 8. Inversion for WA parameters by using data with 30% random noise from 6 profiles. (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The illustration is the same as for Fig.2![]()
图 9 使用3条剖面资料、 数据中加入30%随机噪声后的反演结果．(a) 由慢度公式(5)反演得到；(b) 由偏振公式(6)反演得到； (c) 由慢度公式和偏振公式联合反演得到. 图注说明同图2Figure 9. Inversion for WA parameters by using data with 30% random noise from 3 profiles. (a) Obtained with slowness equation (5); (b) Obtained with polarization equation (6); (c) Obtained by combining equations (5) and (6). The illustration is the same as for Fig.23. 实际数据反演
把上面的反演方法应用到在爪哇海(Java Sea)地区获得的一条walkaway VSP剖面中(Horne,Leaney,2000)． 剖面上布设了228个震源，分布在钻孔两侧-2.5—2.5 km的范围内，相邻震源间隔约为25 m． 以钻孔1.63 km为中心布设5个三分量检波器，相邻检波器间距为5 m． 数据由下行和上行(反射)qP波和qS波组成，由Esmersoy(1990)和Leaney(1990)提出的参数反演方法提取． 本文仅仅研究qP波问题，并且假定地下介质是横向非均匀、 弱各向异性介质. 在这种情况下只能从观测记录中得到慢度矢量的垂向分量和偏振矢量． 通过在式(5)和式(6)中消去慢度矢量的水平分量，可以得到由慢度矢量的垂向分量和偏振矢量表示的反演公式(Zheng，Psencík，2002)． 因为只有一条剖面，所以仅能反演5个WA参数，即εx,εz,δx,ε15和ε35(Zheng，Psencík，2002). 这5个WA参数完全决定介质在(x,z)平面内的性质．
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
从walkaway VSP剖面中得到了228个下行qP波和228个上行qP波数据(图10)(Horne,Leaney,2000)． 图10中纵轴表示慢度矢量的垂直分量，横轴表示偏振角． 偏振角在-90°―90°之间的数据为下行波，偏振角在±(90°―180°)之间的数据为上行波(反射波)． 从图10中可以看出，上行波比下行波有较大的离散性． 图中实线是联合使用上行波和下行波反演得到的理论结果． 在反演中假定介质是一般各向异性介质．
![]()
图 10 来自爪哇海地区的一条变井源距观测剖面Figure 10. A multi-source offset VSP experiment from the Java Sea region在qP波偏振角0°—75°范围内可用的下行波和上行波数目分别为133个和170个． 偏振角大于75°的数据误差较大，因为在这个范围内，慢度矢量和偏振矢量的垂直分量较小，信噪比较低． 可以单独使用下行波组成133个线性方程组，也可以联合使用下行波和上行波组成303个线性方程组． 对前面描述的由5个WA参数组成的方程进行求解，可以获得相关的WA参数． 使用上面公式得到的参考介质的P波速度为α=2.75 km/s． 图11给出了介质为一般各向异性介质模型时得到的(x,z)平面内的相速度曲线． 图中也给出了Horne和Leaney(2000)使用VTI介质模型和不同反演方法得到的结果． 当介质为各向同性时，相速度为常数，在图11中显示为一条直线． Horne和Leaney(2000)假定介质是VTI介质，单独使用慢度数据和联合使用慢度与偏振数据得到了两个稍有差别的结果，相速度在水平方向较为一致，但是在垂直方向有较大的区别． 图11中的细实线和粗实线分别表示使用下行波和联合使用下行波和上行波得到的相速度曲线． 与Horne和Leaney(2000)结果的主要区别在于: 他们得到介质的各向异性为14%(单独使用慢度)和19%(联合使用慢度和偏振); 而本文通过求解前面描述的反演方程得到的介质各向异性为8%． 本文得到的相速度的最小值也不在垂直方向，而是偏离垂直方向大约20°，这一方向可能是对称轴在(x,z)平面内的投影．
4. 讨论与结论
合成数据实验表明，本文提出的反演方法能够确定具有任意对称性的弱各向异性参数，尽管在反演时假定慢度矢量的切向分量为零． 使用较少的剖面表明联合使用慢度公式和偏振公式可以得到较好的结果． 噪声实验表明，慢度公式是确定各向异性参数的较为可靠的工具．
显然，肯定和证实上述结论需要进一步的实验． 笔者希望继续进行具有不规则震源剖面分布和减少震源数目的实验，探讨介质横向非均匀性和低对称性介质对反演的影响． 我们计划研究那些使慢度矢量严重偏离传播面的地震各向异性介质．
上面的实验可以很容易地推广到钻孔为非垂直的和震源高程不同的情况． 本文已经将介质垂向非均匀性的条件扩展到了介质的横向非均匀性，由于使用了慢度分量和偏振矢量，使得在反演中不用考虑上覆介质的影响，避免了复杂的射线追踪计算． 除了介质是弱各向异性的假设条件外，本文提出的正演公式和反演公式具有普遍性．
-
![]()
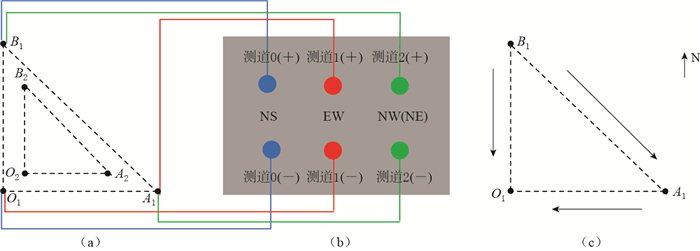
图 1 中国大陆地电场观测装置及连接方式
(a)双等腰三角形布极系统；(b)电极与仪器连接方式；(c)地电场正方向(箭头所指方向)示意图
Figure 1. Observation device of geoelectric field used in Chinese mainland and its connection mode
(a) Double "isosceles triangule" electrodes layout; (b) The connection mode between electrodes and instrument; (c) Positive direction (the arrow pointing direction) for geoelectric field
![]()
图 2 江苏海安台(a，c)和甘肃古丰台(b，d)NS测向地电场日变波形及其叠加图
Figure 2. Geoelectric field waveforms in NS orientation and the overlay maps of Hai'an station in Jiangsu Province (a, c) and Gufeng station in Gansu Province (b, d)
![]()
图 3 2015年4月6—8日地电场日变波形相位对比图
(a)瓜州台；(b)高邮台；(c)银川台；(d)陵阳台
Figure 3. Phase contrast of geoelectric field diurnal waveforms in April 6-8, 2015
(a) Guazhou station; (b) Gaoyou station; (c) Yinchuan station; (d) Lingyang station
![]()
图 4 不同电荷流动优势方向下正交测向(NS和EW)地电场日变波形的相位关系原理示意图(红色箭头表示裂隙优势方位，下同)
(a) NW向；(b) NE向；(c) N向；(d) E向
Figure 4. Phase correlation principle diagram of orthogonal (NS and EW) geoelectric field diurnal waveforms in different dominant orientations of charge movement (red arrows represent dominant orientation of rock crack, the same below)
(a) NW direction; (b) NE direction; (c) N direction; (d) E direction
![]()
图 5 不同电荷流动优势方向下斜测向(NW)与正交测向(NS和EW)地电场日变波形相位关系原理示意图
(a) NW向；(b) NE向(α < N45°E)；(c) NE向(α > N45°E)；(d) N向；(e) E向
Figure 5. Principle diagram of phase correlation between oblique (NW) and orthogonal (NS and EW) geoelectric field diurnal waveforms in different dominant orientations of charge movement
(a) NW direction; (b) NE direction (α < N45°E); (c) NE direction (α > N45°E); (d) N direction; (e) E direction
![]()
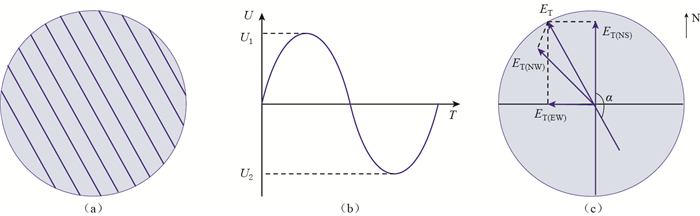
图 6 多测向地电场日变波形相位关系分析的物理模型
(a)裂隙优势方位排列示意图；(b)裂隙水(电荷)渗流(移动)的周期性；(c)地电场ET及其在各测向的分量
Figure 6. Physical model of phase correlation analysis of multi-orientation geoelectric field diurnal waveforms
(a) Sketch of crack dominant orientation; (b) Periodicity of crack water seepage or electric charges movement; (c) Geoelectric field ET and its components in each orientation
![]()
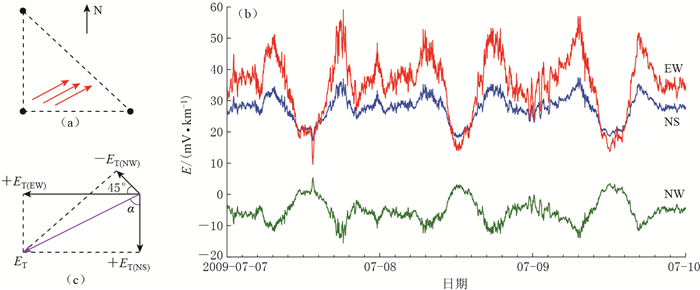
图 7 平凉台各测向地电场日变波形相位关系分析图
(a)布极方式及裂隙优势方位；(b) NS，EW和NW测向的地电场日变波形；(c) ET与各分量的矢量关系
Figure 7. Analysis of phase correlation of geoelectric field diurnal waveforms in different orientations at Pingliang station
(a) Layout of electrodes and dominant crack orientation; (b) Geoelectric field diurnal waveforms in NS, EW, and NW orientations; (c) Vector relations between ET and each component
![]()
图 8 平凉台各测向地电场日变波形
Figure 8. Geoelectric field diurnal waveforms in each orientation at Pingliang station
表 1 2015年1—10月4个台站NS和EW测向观测到的地电场日变波形相位关系的稳定性统计
Table 1 Statistics on phase correlation stability of geoelectric field diurnal waveforms in NS and EW orientations at the four stations from January to October of 2015
台站 日变波形类型 日变波形相位关系 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 瓜州 TGF-B + + + + + + + + + + 高邮 TGF-A + + + + + + + + + + 银川 TGF-B - - - - - - - - - - 陵阳 TGF-A - - - - - - - - - - 注：“+”表示相位相同，“-”表示相位相反. 
下载: 导出CSV
表 2 2009年7月7日平凉台3个测向潮汐谐波振幅和的矢量关系
Table 2 Vector relations of the sum of tidal harmonic amplitudes in the three orientations for Pingliang station on July 7, 2009
测向 日变波形 α E′T分量
/(mV·km-1)E′T
/(mV·km-1)γEW/NW γEW/NS γNW/NS EW TGF-B 13.16 14.27 NW TGF-B N67.25°E 5.40 14.26 -0.99 0.99 -0.99 NS TGF-B 5.67 14.66
下载: 导出CSV
-
安张辉, 元丽华, 李宁, 范莹莹, 谭大诚, 陈军营, 郑国磊. 2010. HHT方法在地电场数据处理中的应用[J].地球物理学进展, 25(2): 525-532. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201002023.htm An Z H, Yuan L H, Li N, Fan Y Y, Tan D C, Chen J Y, Zheng G L. 2010. Discussion on the application of HHT method to geoelectric field data processing[J]. Progress in Geophysics, 25(2): 525-532 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201002023.htm
陈小斌, 赵国泽. 2009.自动构建大地电磁二维反演的测点中心网格[J].地球物理学报, 52(6): 1564-1572. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200906019.htm Chen X B, Zhao G Z. 2009. Automatic construction of a site-centered grid (SCG) for 2D magnetotelluric inversion[J]. Chinese Journal of Geophysics, 52(6): 1564-1572 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200906019.htm
范莹莹, 杜学彬, Zlotnicki J, 谭大诚, 刘君, 安张辉, 陈军营, 郑国磊, 解滔. 2010.汶川MS8.0大震前的电磁现象[J].地球物理学报, 53(12): 2887-2898. doi: 10.3969/j.issn.0001-5733.2010.12.012 Fan Y Y, Du X B, Zlotnicki J, Tan D C, Liu J, An Z H, Chen J Y, Zheng G L, Xie T. 2010. The electromagnetic phenomena before the MS8.0 Wenchuan earthquake[J]. Chinese Journal of Geophysics, 53(12): 2887-2898 (in Chinese). doi: 10.3969/j.issn.0001-5733.2010.12.012
黄清华, 刘涛. 2006.新岛台地电场的潮汐响应与地震[J].地球物理学报, 49(6): 1745-1754. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200606021.htm Huang Q H, Liu T. 2006. Earthquakes and tide response of geoelectric potential field at the Niijima station[J]. Chinese Journal of Geophysics, 49(6): 1745-1754 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200606021.htm
刘君, 杜学彬, Zlotnicki J, 范莹莹, 安张辉, 解滔, 郑国磊, 谭大诚, 陈军营. 2011.几次大震前的地面和空间电磁场变化[J].地球物理学报, 54(11): 2885-2897. doi: 10.3969/j.issn.0001-5733.2011.11.018 Liu J, Du X B, Zlotnicki J, Fan Y Y, An Z H, Xie T, Zheng G L, Tan D C, Chen J Y. 2011. The changes of the ground and ionosphere electric/magnetic fields before several great earthquakes[J]. Chinese Journal of Geophysics, 54(11): 2885-2897 (in Chinese). doi: 10.3969/j.issn.0001-5733.2011.11.018
马钦忠, 冯志生, 宋治平, 赵卫国. 2004.崇明与南京台震前地电场变化异常分析[J].地震学报, 26(3): 304-312. http://www.dzxb.org/Magazine/Show?id=26631 Ma Q Z, Feng Z S, Song Z P, Zhao W G. 2004. Study on the variation characteristics of the geoelectric field preceding earthquakes[J]. Acta Seismologica Sinica, 26(3): 304-312 (in Chinese). http://www.dzxb.org/Magazine/Show?id=26631
马钦忠. 2008.地电场多极距观测装置系统与文安MS5.1地震前首都圈地电场异常研究[J].地震学报, 30(6): 615-625. http://www.dzxb.org/Magazine/Show?id=27081 Ma Q Z. 2008. Multi dipole observation system and study on the abnormal variation of the geoelectric field observed at Capital Network before the 2006 Wen'an, Hebei of China, MS5.1 earthquake[J]. Acta Seismologica Sinica, 30(6): 615-625 (in Chinese). http://www.dzxb.org/Magazine/Show?id=27081
毛桐恩, 席继楼, 王燕琼, 尹淑芝. 1999.地震过程中的大地电场变化特征[J].地球物理学报, 42(4): 520-528. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX199904010.htm Mao T E, Xi J L, Wang Y Q, Yin S Z. 1999. The variation characteristics of the telluric field in the process of earthquake[J]. Chinese Journal of Geophysics, 42(4): 520-528 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX199904010.htm
钱家栋, 陈有发, 金安忠. 1985.地电阻率法在地震预报中的应用[M].北京:地震出版社: 38-47. Qian J D, Chen Y F, Jin A Z. 1985. The Application of Resistivity Method in Earthquake Prediction[M]. Beijing: Seismological Press: 38-47 (in Chinese).
孙正江, 王华俊. 1984.地电概论[M].北京:地震出版社: 23-28. Sun Z J, Wang H J. 1984. An Introduction to Geoelectricity[M]. Beijing: Seismological Press: 23-28 (in Chinese).
谭大诚, 赵家骝, 席继楼, 杜学彬, 徐建明. 2010.潮汐地电场特征及机理研究[J].地球物理学报, 53(3): 544-555. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201003010.htm Tan D C, Zhao J L, Xi J L, Du X B, Xu J M. 2010. A study on feature and mechanism of the tidal geoelectrical field[J]. Chinese Journal of Geophysics, 53(3): 544-555 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201003010.htm
谭大诚, 王兰炜, 赵家骝, 席继楼, 刘大鹏, 于华, 陈军营. 2011.潮汐地电场谐波和各向波形的影响要素[J].地球物理学报, 54(7): 1842-1853. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201107019.htm Tan D C, Wang L W, Zhao J L, Xi J L, Liu D P, Yu H, Chen J Y. 2011. Influence factors of harmonic waves and directional waveforms of tidal geoelectrical field[J]. Chinese Journal of Geophysics, 54(7): 1842-1853 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201107019.htm
谭大诚, 赵家骝, 席继楼, 刘大鹏, 安张辉. 2012.青藏高原中强地震前的地电场变异及构成解析[J].地球物理学报, 55(3): 875-885. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201203016.htm Tan D C, Zhao J L, Xi J L, Liu D P, An Z H. 2012. The variation of waveform and analysis of composition for the geoelectrical field before moderate or strong earthquakes in Qinghai-Tibetan Plateau regions[J]. Chinese Journal of Geophysics, 55(3): 875-885. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201203016.htm
谭大诚, 席继楼, 张慧, 王兰炜, 范莹莹, 安海静. 2013.地电场水文地质因素及裂隙水主体渗流方向逐日计算[J].地震学报, 35(1): 36-49. http://www.dzxb.org/Magazine/Show?id=28815 Tan D C, Xi J L, Zhang H, Wang L W, Fan Y Y, An H J. 2013. Hydrogeologic factors of geoelectric field and diurnal computation of preferred orientation of crack water seepage[J]. Acta Seismologica Sinica, 35(1): 36-49 (in Chinese). http://www.dzxb.org/Magazine/Show?id=28815
谭大诚, 赵家骝, 刘小凤, 范莹莹, 刘君, 陈军营. 2014.自然电场的区域性变化特征[J].地球物理学报, 57(5): 1588-1598. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201405022.htm Tan D C, Zhao J L, Liu X F, Fan Y Y, Liu J, Chen J Y. 2014. Features of regional variations of the spontaneous field[J]. Chinese Journal of Geophysics, 57(5): 1588-1598 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201405022.htm
汤吉, 詹艳, 王立凤, 董泽义, 赵国泽, 徐建郎. 2010.汶川地震强余震的电磁同震效应[J].地球物理学报, 53(3): 526-534. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201003008.htm Tang J, Zhan Y, Wang L F, Dong Z Y, Zhao G Z, Xu J L. 2010. Electromagnetic coseismic effect associated with aftershock of Wenchuan MS8.0 earthquake[J]. Chinese Journal of Geophysics, 53(3): 526-534 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201003008.htm
王书明, 李德山, 胡浩. 2013.三维/三维构造下大地电磁相位张量数值模拟[J].地球物理学报, 56(5): 1745-1752. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201305033.htm Wang S M, Li D S, Hu H. 2013. Numerical modeling of magnetotelluric phase tensor in the context of 3D/3D formation[J]. Chinese Journal of Geophysics, 56(5): 1745-1752 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201305033.htm
席继楼, 赵家骝, 王燕琼, 王兰炜, 李艳东. 2002.地电场观测技术研究[J].地震, 22(2): 67-73. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201606045.htm Xi J L, Zhao J L, Wang Y Q, Wang L W, Li Y D. 2002. Research on observational technology of the geoelectric field[J]. Earthquake, 22(2): 67-73 (in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201606045.htm
徐文耀. 1992. Sq发电机电流的逐日变化和Sq指数[J].地球物理学报, 35(6): 676-684. Xu W Y. 1992. Day-to-day variability of the Sq dynamo currents and Sq index[J]. Acta Geophysica Sinica, 35(6): 676-684 (in Chinese).
叶青, 杜学彬, 周克昌, 李宁, 马占虎. 2007.大地电场变化的频谱特征[J].地震学报, 29(4): 382-390. http://www.dzxb.org/Magazine/Show?id=26427 Ye Q, Du X B, Zhou K C, Li N, Ma Z H. 2007. Spectrum characteristics of geoelectric field variation[J]. Acta Seismologica Sinica, 29(4): 382-390 (in Chinese). http://www.dzxb.org/Magazine/Show?id=26427
张学民, 翟彦忠, 郭学增, 郭建芳. 2007.远震前的地电场潮汐波异常[J].地震学报, 29(1): 48-58. http://www.dzxb.org/Magazine/Show?id=26399 Zhang X M, Zhai Y Z, Guo X Z, Guo J F. 2007. Tidal wave anomalies of geoelectrical field before remote earthquakes[J]. Acta Seismologica Sinica, 29(1): 48-58 (in Chinese). http://www.dzxb.org/Magazine/Show?id=26399
赵国泽, 陈小斌, 肖骑彬, 王立凤, 汤吉, 詹艳, 王继军, 张继红, Utada H, Uyeshima M. 2009.汶川MS8.0级地震成因三"层次"分析:基于深部电性结构[J].地球物理学报, 52(2): 553-563. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dqwx200902028&dbname=CJFD&dbcode=CJFQ Zhao G Z, Chen X B, Xiao Q B, Wang L F, Tang J, Zhan Y, Wang J J, Zhang J H, Utada H, Uyeshima M. 2009. Generation mechanism of Wenchuan strong earthquake of MS8.0 inferred from EM measurements in three levels[J]. Chinese Journal of Geophysics, 52(2): 553-563 (in Chinese). http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dqwx200902028&dbname=CJFD&dbcode=CJFQ
中国地震局. 2006. DB/T 18. 2—2006地震台站建设规范, 地电台站, 第2部分: 地电场台站[S]. 北京: 地震出版社: 6-7. China Earthquake Administration. 2006. DB/T 18.2-2006 Specification for the Construction of Seismic Station, Geoelectrical Station, Part 2: Geoelectrical Field Observatory[S]. Beijing: Seismological Press: 6-7 (in Chinese).
Varotsos P, Alexopoulos K. 1984a. Physical properties of the variations of the electric field of the earth preceding earthquakes, Ⅰ[J]. Tectonophysics, 110(1/2): 73-98. http://www.sciencedirect.com/science/article/pii/0040195184900593
Varotsos P, Alexopoulos K. 1984b. Physical properties of the variations of the electric field of the earth preceding earthquakes, Ⅱ. Determination of epicenter and magnitude[J]. Tectonophysics, 110(1/2): 99-125. http://www.sciencedirect.com/science/article/pii/004019518490060X
-
期刊类型引用(9)
1. 王玮铭，廖晓峰，任越霞. 四川江油台地电场优势方位角异常核实与分析. 四川地震. 2024(01): 7-12 . 
百度学术
2. 刘海洋，饶文，徐衍刚，艾萨·伊斯马伊力. 2024年1月23日乌什M_S7.1地震前新疆地电优势方位角变化特征分析. 内陆地震. 2024(02): 182-193 . 百度学术
3. 李瑞卿，郭学增，李凤，张蕾，信世民，尹宏伟. 兴济地震台大地电场方位变化特征. 华北地震科学. 2023(03): 91-96 . 百度学术
4. 杜学彬，张元生，谭大诚，安张辉，王建军，范莹莹，刘君，陈军营. 国际地震和火山电磁方法组织2016年兰州研讨会——纪念兰州地震研究所开创地电监测预报地震半个多世纪. 地震工程学报. 2022(01): 244-250 . 百度学术
5. 王宇，谭大诚，邱大琼，张锋，陈亮. 2020年新疆于田M_S6.4地震和田台地电场异常的测道差异性. 地震. 2021(02): 180-189 . 百度学术
6. 艾萨·伊斯马伊力，陈界宏，毛志强. 2016—2017年北天山地区两次6级地震前地电场异常. 电波科学学报. 2020(03): 430-436 . 百度学术
7. 王玮铭，谭大诚. 2019年长宁M_S6.0地震邻区分钟采样地电场分析. 地震. 2020(03): 41-51 . 百度学术
8. 邹广，陈亮，牛中华. 2020年6月26日新疆于田M_S6.4地震地电场异常分析. 内陆地震. 2020(03): 310-316 . 百度学术
9. 王玮铭，谭大诚. 同场地多方位多极距地电场相关特性. 地震学报. 2020(04): 419-434+509 . 本站查看
其他类型引用(5)
计量
- 文章访问数: 641
- HTML全文浏览量: 273
- PDF下载量: 20
- 被引次数: 14
