Joint iterative inversion of tectonic stress field and fault identification in Yingjiang area
-
摘要: 搜集了盈江及其邻区5组地震序列震源机制解并反演得到该区域的构造应力场。研究结果显示：盈江地区整体主压应力以NNE向为主，主张应力以ESE向为主；但其局部应力场不完全一致，沿苏典断裂分布的主压应力轴走向随着断裂走向由北向南延伸角度逐渐向北偏移，而盈江地区的西南部，其主压应力走向更偏向于东，这可能与大盈江断裂的横向拉伸有关。此外，本研究通过应力场反演识别出了5组地震序列震源机制解的主发震断层节面的走向、倾角、滑动角及发震断层的摩擦系数，为今后该区域的地震研究及地壳动力学变迁提供了参考。Abstract: There has always been a problem in inversion of tectonic stress field by focal mechanism solution, it is impossible to determine which nodel plane is the correct seismogenic fault plane. The joint iterative stress inversion method can effectively avoid the error caused by incorrect fault selection by identifying the fault instability. In this paper, the focal mechanism solutions of five groups of earthquake sequences in Yingjiang and its adjacent areas are collected, and the tectonic stress field in this area is inversed. The results show that, in Yingjiang area, the main compressive stress is NNE, and the main tensile stress is ESE, which is basically consistent with the previous research results. However, the local stress field is not completely consistent. The strike of the principal stress axis along the Sudian fault extends from north to south, and the angle gradually shifts to the north. In the southwest of Yingjiang, the strike of the principal stress tends to the East, which may be related to the transverse extension of the Dayingjiang fault. In addition, the strike, dip angle, slip angle and friction coefficient of the main seismogenic fault nodal planes of the focal mechanism solutions of five groups of earthquake sequences are identified by stress field inversion. This provides a valuable reference for the future seismic and crustal dynamic changes research in this region.
-
引言
考虑到大地震的记忆性，Utsu(1972)，Rikitake(1974)和Hagiwara(1974)基于Reid(1910)提出的弹性回跳理论，提出了一种更新模型，该模型假定断层上大地震的复发符合更新过程． 国外研究人员先后提出了多种概率分布来描述这种更新模型，具体的概率分布模型包括高斯分布(Rikitake，1974)、 韦布尔分布(Hagiwara，1974)、 对数正态分布(Nishenko，Buland，1987)、 布朗过程时间(Brownian passage time，简写为BPT)分布(Ellsworth et al，1999； Matthews et al，2002)等模型．
对于任何一种概率分布模型，若已知大震复发的概率密度函数f(T)和最近一次大震的离逝时间Te，则可利用下式计算断层源在未来一段时间ΔT内发生大震的条件概率(Wesnousky，1986)：
(1) 其中，概率密度函数f(T)的参数主要包括大震的平均复发间隔和反映复发间隔T的自然随机不确定性的参数，如标准差σT和变异系数α等．
在大震发生概率计算过程中存在大量的不确定性，例如： 由于活动断裂上的历史地震数据和古地震数据非常有限，由小样本数据所确定的模型参数存在很大的不确定性； 古地震数据的年代测定存在不确定性； 古地震的完整性存在不确定性； 大震发生概率模型本身也存在一定的不确定性． 然而，在实际大震发生概率计算过程中对不确定性的考虑仍不足，例如： 一般不考虑T，Te等参数的不确定性，而是较主观地采用一个固定值； 一般不考虑古地震的完整性，而是较武断地假定某时段内的古地震是完整的．
不确定性一般可分为认知不确定性和随机不确定性，本文在此基础上又对不确定性的定量化过程和处理过程分别进行了深入分析． 按照概率分布类型不同，将不确定性分布分为连续型分布和离散型分布;按照认知主体的不同，将不确定性的处理分为对个体自身认知不确定性的处理和对不同个体之间认知差异性的处理．最后进一步探讨了具体的不确定性处理方法和原则．
此外，大震发生概率计算过程中的不确定性构成往往很复杂，例如，不确定性因素较多，而不同不确定性因素之间又存在相关性，这使得利用数值方法实现起来比较困难． 针对该问题，本文首先提出利用蒙特卡罗模拟法对大震发生概率模型中的各种不确定性分布直接进行反复随机抽样； 然后，通过对大量的随机模拟结果进行统计分析，得到最终的大震发生概率计算结果； 最后，以东昆仑断裂带塔藏段的大震发生概率为计算实例，在充分考虑各种不确定性的基础上，建立了塔藏段的大震发生概率模型，并利用蒙特卡罗法计算塔藏段未来100年的大震发生概率．
1. 大震发生概率模型的不确定性分析
1.1 不确定性分类
在各种地震危险性模型中，对于不确定性的划分，一般可分为随机不确定性和认知不确定性(Bommer，2003)． 随机不确定性反映的是自然本身所固有的各种随机性； 认知不确定性反映的是基于不完备的信息和知识，人的主观认知和判断的不准确性．
大震危险性分析中的不确定性分析是对不确定性进行定量化处理，进而在大震危险性分析中考虑各种不确定性因素． 随机不确定性和认知不确定性有时可以分离，有时则很难分离． 因此，为了探讨不确定性的具体处理方法，本文在不确定性处理过程中，分别按照概率分布类型的不同和认知主体的不同进行划分，而未将随机不确定性和认知不确定性分离开进行讨论．
首先，按照概率分布类型不同，本文将不确定性分布分为连续型分布和离散型分布． 对于不确定性的定量化描述，根据具体情况的不同，可以采用连续型分布，也可以采用离散型分布． 其中，连续型分布更为客观，但建立相对可靠的分布模型需要足够的样本支持，同时连续型的概率分布不方便计算； 离散型分布的确定相对主观，但却便于计算． 其次，按照认知主体的不同，本文将不确定性的处理分为对个体自身认知不确定性的处理和对不同个体之间认知差异性的处理． 在不确定性的实际处理中，不仅要考虑研究个体，同时还需考虑不同研究人员之间所得出的不确定性定量化结果的差异性(Senior Seismic Hazard Analysis Committee，1997)． 这种差异性反映的是人与人之间存在的认知分歧，为了避免计算结果过于主观和片面，需要在大震危险性分析中考虑这种分歧．
1.2 不确定性的处理方法
为便于讨论不确定性的具体处理方法，根据本文所采用的分类方式，并参考前人在概率地震危险性分析中不确定性处理方面的研究成果(Senior Seismic Hazard Analysis Committee，1997)，本文对不确定性的处理过程参见图 1.
1.2.1 采用连续型分布来定量化不确定性
连续型分布较离散型分布更为精确，但其计算量较大，因此如果计算条件允许，可以采用连续型分布来定量化不确定性． 连续型分布的具体分布形态又分为均匀分布和非均匀分布．
1) 均匀分布. 客观信息量越少，不确定性越大，这是个不变的原则，必须体现在大震危险性分析中的每个具体环节中． 对于基本不可知因素或完全不可知因素的不确定性评价，一般采用均匀加权法，其本质上属于拉普拉斯决策法，即等可能决策法． 均匀分布在实际地震危险性分析中应用广泛，例如： 在潜在震源区内任何地方发生地震的可能性是相同的(Cornell，1968)； 古地震发生在其年代测定不确定性的上下限内任意一年的可能性也是相同的．
2)非均匀分布. 若要用非均匀分布来表示不确定性，首先必须假设一个非均匀分布模型，然后通过参数估计法确定该分布模型的参数． 具体的参数估计法包括矩估计、 最大似然估计、 贝叶斯估计等． 其中矩估计和最大似然估计多用于计算某些自然随机分布的参数，而贝叶斯估计则多用于计算某些模型参数的认知不确定性分布． 如果有连续性的证据或数据，则可以采用非均匀分布来表示不确定性，但必须先定义一个分布模型，甚至是出于个体的主观认识．
1.2.2 采用离散型分布来定量化不确定性
逻辑树是一种常用的离散化不确定性处理方法． 该方法一般分为两种： 一种是加权逻辑树法，一种是不加权逻辑树法．
1) 不加权逻辑树． 对于个体的认知不确定性处理，类似于连续型分布中的均匀分布，不加权逻辑树也是一种等可能加权． 对于不同个体之间的认知不确定性的差异性处理，可以采用不加权逻辑树，这意味着在决策过程中不同个体的认知被赋予相同的权重，即不同个体之间是平等的．
2)加权逻辑树． 利用加权逻辑树对个体认知不确定性的处理，是单独地研究个体基于有限的地震地质资料和信息，对大震危险性评估过程中某个环节的认知不确定性分布所作的离散处理，其中每个逻辑树分支均被主观地赋予一定的权重． 根据有限的地震地质资料和信息，对两种或两种以上可能(或离散型的参数值)的权重进行主观评定． 最终评定结果的确定须参考信息的完备程度，信息量越少，未知因素越多，不确定性也就越大． 例如，某个不确定性环节包括A和B两种可能，即使所有的已知信息均支持A，但如果信息量非常有限，也不可以给出确定的结论，而应参考信息量的完备程度，在充分考虑不确定性的基础上进行权重评估．
对于个体之间的认知不确定性的差异性处理，也可以采用加权逻辑树法，其综合了不同个体认知的权重不平等性和单独个体的认知不确定性． 此外，在不确定性处理过程中还需注意以下两点：
1) 必须保证权重赋予和不确定性分布范围确定过程的一致性原则． 一个独立的人或者独立的小组，在大震危险性评估过程中每个具体的不确定性环节，必须遵循相同的不确定分级原则或权重分配原则．
2) 在评估不确定性分布范围的过程中，需要保守考虑，但又不可以无限地保守． 一些概率极低的极端事件对计算结果的贡献很小，也很难进行概率评估和计算，所以，在实际大震危险性评估过程中可以对不确定性分布作适当的截断处理．
2. 计算实例
本文以东昆仑断裂带东段塔藏段的大震发生概率为计算实例，具体研究在大震发生概率计算过程中如何考虑不确定性．
2.1 东昆仑断裂带塔藏段的古地震
东昆仑断裂带东段位于巴颜喀拉地块与西秦岭地块边界断裂的东段，全长约330 km，自西向东可划分为3段： 玛沁段、 玛曲段和塔藏段(青海省地震局，中国地震局地壳应力研究所，1999)． 国内外研究人员在东昆仑断裂带东段上获得了许多古地震数据，为评估该段的大地震发生概率提供了重要依据． 其中，玛沁段和玛曲段上的古地震数据比较丰富，而塔藏段上的古地震数据量则比较少，完整性较差，最近一次大震的离逝时间也存在很大的不确定性．
根据李正芳等(2012)对前人古地震研究结果的分析，本文给出了塔藏段古地震的发生时间分别为距今(4693±151)年，(7304±500)年和(9136±131)年，其中存在4700年左右的大地震空白期，很可能存在历史地震漏记的现象． 另根据李正芳等(2012)对四川松潘(位于塔藏段东南方向约50 km)历史文献记载的分析，推断塔藏段最近一次地震的发生时间应在公元638年之前，即最近一次地震的离逝时间应介于1377—(4693±151)年之间．
2.2 不确定性分析
由于塔藏段古地震数据量比较少，完整性较差，不管是大震复发间隔还是大震离逝时间，均存在着非常大的不确定性． 具体的不确定性因素包括以下3个方面：
1) 在离逝时间Te的确定过程中，需要考虑古地震记录和历史地震记载的不完整性所造成的最近一次大地震发生年代的不确定性
首先，古地震的完整性研究一直是古地震研究的难题，不同断裂上的古地震研究深度不同，地层的完整性情况也不同，造成不同断裂和不同时段的古地震记录的完整性情况相差较大(冉勇康，邓起东，1999)； 其次，我国历史地震资料保存得相对较多，但就各个历史时期和不同区域来说，历史地震记载的完整性程度相差较大(陈春梅，任雪梅，2014)． 因此，无法通过客观的统计分析方法得到最近一次大地震发生时间的不确定性分布，也无法直接判定某时间段内的大震记录是否完整或缺失的数量，只能主观评估已知信息量能否足够(或充分)判定给定时间段的大地震记载是完整的．
本文提出采用逻辑树法来分析由古地震记录和历史地震记载的不完整性所造成离逝时间Te的认知不确定性． 逻辑树在此处共有两个分支： ① 根据已知的区域古地震研究成果和区域历史地震记载情况，无法确定给定时间段的大地震记载是完整的，即信息量有限，无法得出确定性的结论； ② 根据已知的区域古地震研究成果和区域历史地震记载情况，可以确定给定时间段的大地震记载是完整的，即信息量是足够充分的，可以得出确定性的结论． 根据已知的数据和资料，并征求相关方面专家的意见，对两个逻辑树分支的权重进行主观赋值．
2) 在平均复发间隔T的确定过程中，需要考虑古地震年代测定的不确定性. 由于每次古地震发生的年代均存在不确定性，而对于这种不确定性，根据多探槽古地震分析的逐次限定法可以确定古地震发生年代的上下限(毛凤英，张培震，1995)，但很难确定其具体的分布形态，因此可以采用均匀分布来处理此种不确定性．
3) 在平均复发间隔T的确定过程中需要考虑利用有限的复发间隔数据样本来确定平均复发间隔参数的客观认知不确定性．
在利用塔藏段有限的两个复发间隔数据估计T的过程中，需要同时计算基于小样本数据估计参数T的认知不确定性． 本文采用贝叶斯估计法进行评估，具体做法可以参考郭星和潘华(2016)提出的平均复发间隔T的认知不确定性评估方法．
2.3 考虑不确定性的塔藏段大震发生概率计算模型
在Reid(1910)弹性回跳理论的基础上，国内外研究人员先后提出了多种符合更新过程的概率模型，其中比较常用的概率分布模型有对数正态分布模型(Nishenko，Buland，1987)、 BPT(Ellsworth et al，1999； Matthews et al，2002)模型等．
本文未考虑模型本身的不确定性，直接采用BPT模型计算大震发生概率. BPT分布也被称作逆高斯分布(Seshadri，1983)，其概率密度函数为
(2) 式中： T为断裂段大震的平均复发间隔； α为大震复发间隔的变异系数，反映的是大震复发间隔的随机不确定性，可以通过对大量归一化复发间隔数据的统计分析得到． 在广泛搜集的39个原地复发的地震序列基础上，郭星和潘华(2015)统计分析得到了一个通用的变异系数α＝0.34，本文在发震概率计算过程中直接选取α=0.34．
塔藏段3次古地震的发生时间分别为距今(4693±151)年，(7304±500)年和(9136±131)年，本文利用这3个古地震数据来评估BPT模型的参数T，在参数确定过程中的各种不确定性则采用蒙特卡罗法来处理，最后利用式(1)计算塔藏段未来100年的大震发生概率．
参考对不确定性处理方法的分类讨论，本文采用加权逻辑树法来考虑古地震的不完整性． 考虑到每个逻辑树分支所对应的计算过程均存在一定差异，本文分成A和B两个相互独立的蒙特卡罗模拟过程分别进行计算． 其中分支A假定根据有限的信息，无法确定给定时间段的大地震记载是完整的； 分支B假定信息量足够充分，可以确定给定时间段的大地震记载是完整的． 根据已知的数据和资料，并征求相关方面专家的意见，对两个逻辑树分支的权重进行主观赋值．
分支A的具体实现步骤如图 2所示：
![]()
图 2 塔藏段大震发生概率计算的分支A流程图Figure 2. The process chart of branch A for calculating the occurrence probability of large earthquakes on the Tazang fault1) 考虑到古地震年代测定的不确定性所导致的平均复发间隔参数T的不确定性，在3次古地震发生年代的不确定性范围内生成均匀分布的随机数，这样就可以得到两个随机复发间隔数据. 同时还需要得出最近一次已知古地震的离逝时间Te1，这是考虑到最近一次古地震事件年代测定的不确定性，平均复发间隔参数与大震离逝时间参数之间存在一定的相关性，不可以分别得出.
2) 对于平均复发间隔的参数认知不确定性分布的定量化处理，可以参考郭星和潘华(2016)提出的基于两个复发间隔数据所确定的平均复发间隔T的参数认知不确定性研究，具体方法如下：
若已知两个大震复发间隔的实际数据T21和T22，对于任意平均复发间隔T，根据式(2)得到的复发间隔为T21的概率密度函数为
(3) 而复发间隔为T22的概率密度函数为
(4) 再根据贝叶斯估计法，即可得到T的认知不确定性分布的概率密度函数f(T)
(5) 3) 对于任意平均复发间隔T，其所对应的BPT模型的概率密度函数为f(T|T)，因此，根据式(1)其对应的发震概率计算公式需修改为
(6) 根据f(T)，可以随机生成一个平均复发间隔T，也就同时确定了一个f(T|T)．
4) 根据步骤3中确定的概率密度函数f(T|T)，随机生成下一次地震发生的时间Ts． 若要确定当前的大震离逝时间Te，则需进行如下判断： 若Ts＞Te1，当前的大震离逝时间Te=Te1; 若Ts＜Te1-1377，当前的大震离逝时间Te=Ts; 其它情况则需重新模拟，再随机生成下一次地震发生的时间Ts，直到Ts满足上述两种情况为止．
从保守和计算效率的角度考虑，判定过程中并未考虑记载空段内漏记两次或两次以上古地震的小概率特殊事件的发生．
5) 已知f(T|T)和大震离逝时间Te，可以根据式(6)计算得到未来100年塔藏段大震的发生概率Pn．
6)反复模拟10万次，计算出10万次模拟结果的平均值P．
分支B的具体实现步骤与分支A类似(图 3)，只是第4步有所差异，考虑到分支B假定不可能出现古地震漏记，则直接取大震离逝时间Te=Te1．
![]()
图 3 塔藏段大震发生概率计算的分支B流程图Figure 3. The process chart of branch B for calculating the occurrence probability of large earthquakes on the Tazang fault2.4 大震发生概率计算结果
分支A的大震发生概率计算结果为0.11； 分支B的大震发生概率计算结果为0.16． 而对于A和B两个逻辑分支的权重赋值则需要综合考虑以下几个方面： ① 研究区域的人类活动历史和历史地震记载的完整性情况； ② 研究断裂上的地层完整性情况； ③ 研究断裂上的古地震研究深度．
基于上述3个方面的信息，并征求相关方面专家的意见，本文给出的A和B两个逻辑分支的权重赋值WA和WB分别为0.8和0.2，最后计算出的塔藏段未来100年的大震发生概率为
(8) 3. 讨论与结论
本文对大震发生概率评估过程中的各种不确定性进行了系统分析，在认知不确定性和随机不确定性的基础上对不确定性的定量化处理过程进行了分类研究，并对不确定性的具体定量化方法进行了梳理．
考虑到大震复发概率计算过程中存在大量的不确定性，且不确定性的构成又较为复杂，数值方法实现起来比较困难，故此类不确定性往往被忽略掉． 本文首先明确了大震复发概率模型中的各种不确定性，特别是常被忽略的不确定性，然后利用蒙特卡罗模拟法对大震发生概率模型中的各种定量化的不确定性直接进行随机抽样，最后通过对大量随机模拟结果的统计分析得到了最终的大震发生概率计算结果． 虽然计算过程相对复杂，但可以尽可能地减少一些主观因素，使得计算结果更为客观．
本研究的重点在于探讨如何利用蒙特卡罗法考虑发震概率计算过程中的各种不确定性，对于各个不确定性分支的具体赋值过程则未进行更深入的研究． 而不确定性分支的权重将直接影响最终的计算结果，需要作大量的地震地质调查和统计分析工作，也需要采取科学有效的方法对多位专家的意见进行综合． 在实际大震危险性评估中，怎样考虑和处理这种人与人之间的认知分歧，也需进一步研究．
-
![]()
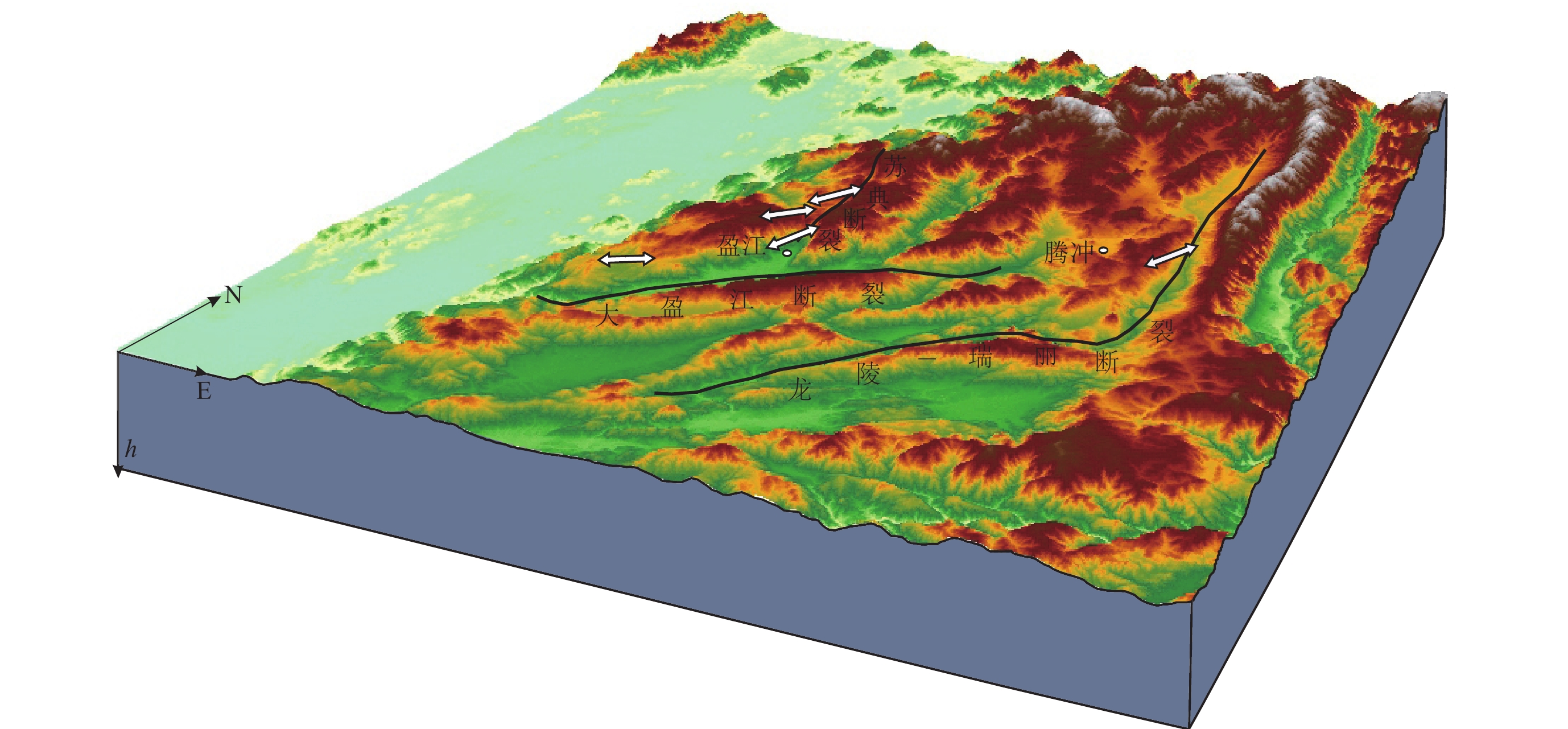
图 1 盈江区域地震序列震源机制解空间分布图
F1：怒江断裂；F2：龙陵—瑞丽断裂；F3：瓦德龙断裂；F4：大盈江断裂；F5：昔马—盘龙山断裂；F6：苏典断裂；F7：槟榔断裂；F8：猴桥—中和断裂；F9：固东—腾冲断裂图中A−E区分别代表2008年3月21日、8月21日及9月3日盈江地震序列、2011年3月10日盈江地震序列和2011年8月9日腾冲地震序列的震源机制解分区
Figure 1. Spatial distribution of focal mechanism solutions of earthquake sequences in Yingjiang region
F1：Nujiang fault；F2：Longling-Ruili fault；F3：Wadelon fault；F4：Dayingjiang fault；F5：Xima-Panlongshan fault；F6：Sudian fault；F7：Binglang fault；F8：Houqiao-Zhonghe fault；F9：Gudong-Tengchong fault.A−E in the figure represent the focal mechanism solution partition of Yingjiang earthquake sequences on 21 March 2008，21 August 2008，3 September 2008，10 March 2011 and Tengchong earthquake sequence on 9August 2011，respectively
![]()
图 2 断层不稳定性的莫尔圆定义（Vavryčuk，2014）
红色圆点标出了以不稳定性为特征I＝1的主断层上的牵引力，蓝色圆点标出了以任意不稳定性为特征I的主断层上的牵引力
Figure 2. Definition of the fault instability in Mohr’s diagram （Vavryčuk，2014）
The red solid circle marks the traction on the main fault characterized by instability I＝1，and the blue solid circle marks the traction on the main fault characterized by arbitrary instability
![]()
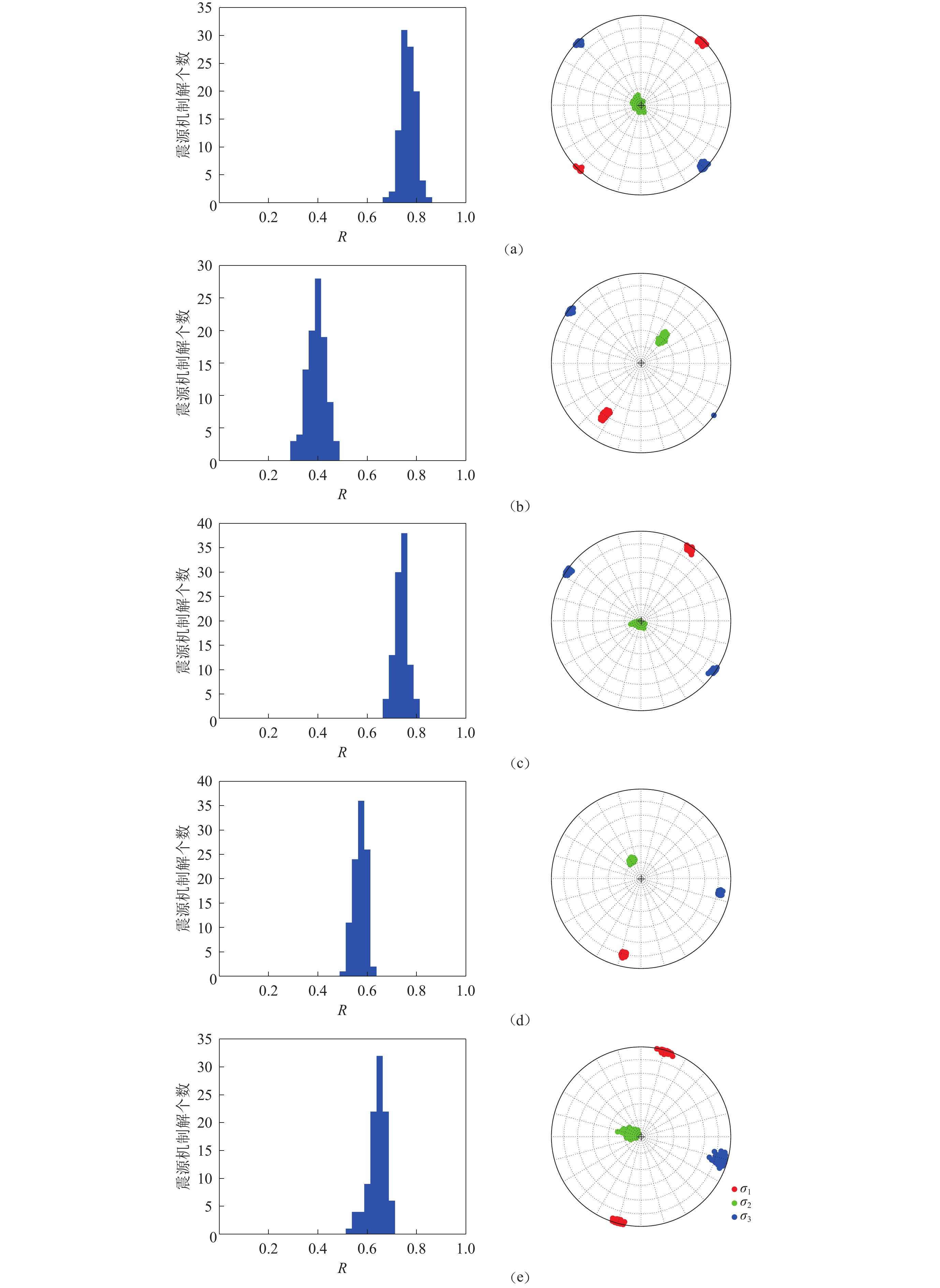
图 3 A—E区（a—e）5组地震序列震源机制解联合迭代反演的应力场结果
左侧为地震序列震源机制解反演的断层摩尔圆分布，右侧为主轴方向及P，T轴
Figure 3. Stress field results of joint iterative inversion for focal mechanism solutions of five seismic sequences in areas A−E （a−e）
The left side is the fault Mohr’s circle distribution inversed by focal mechanism solutions of seismi sequences， and the right side is the main axis direction and P，T axis
![]()
图 4 5组地震序列构造应力场反演的应力形因子R的分布（左）及主应力轴方向（右）
Figure 4. Stress shape factor R distribution （left） and principal stress axis direction （right） of tectonic stress field inversion results for five earthquake sequences
（a） 2008-13-21；（b） 2008-08-21；（c） 2008-09-03；（d） 2011-03-10；（e） 2011-08-09
![]()
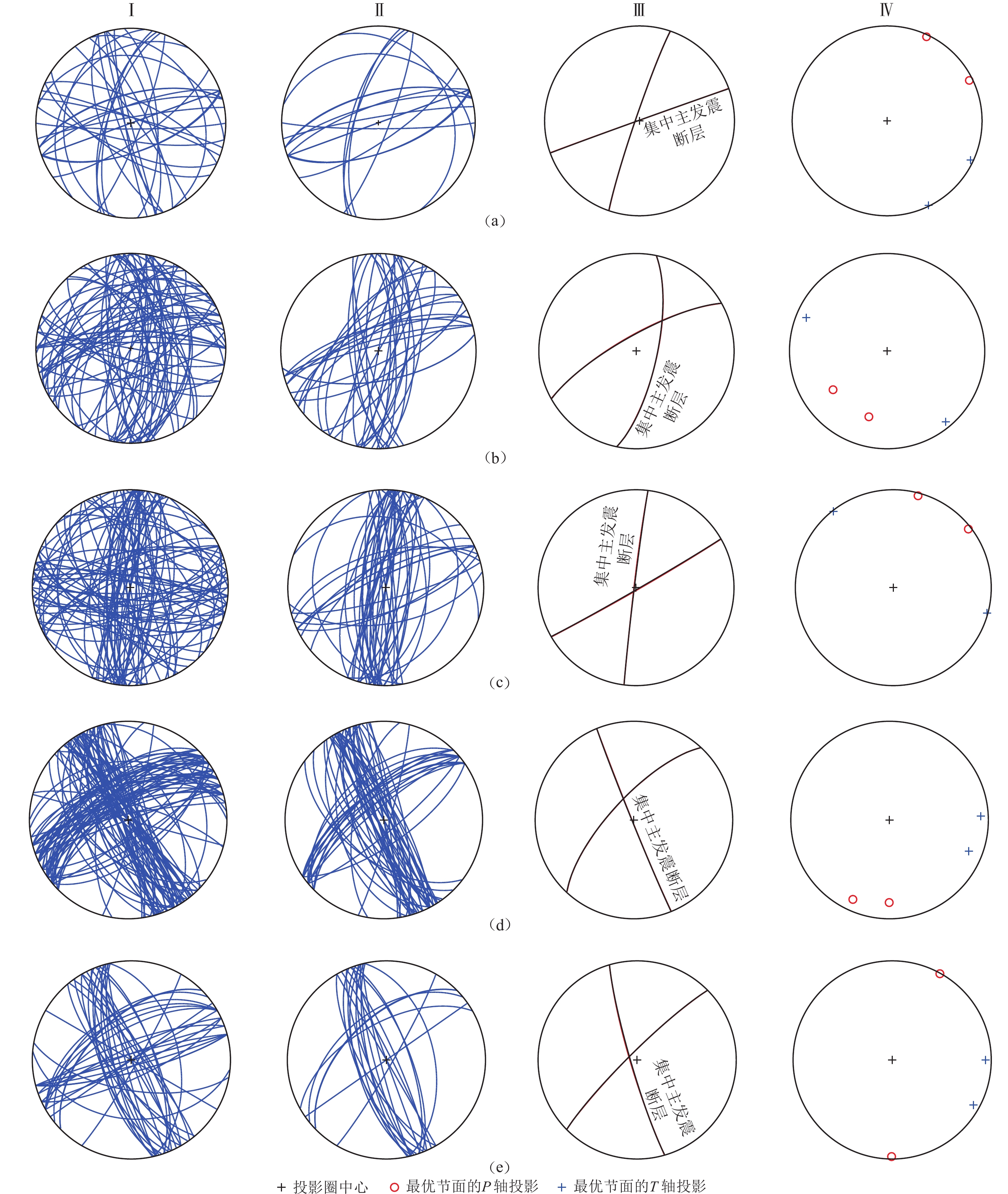
图 5 5组地震序列震源机制解应力反演识别出的主断层节面图
Ⅰ ：地震序列震源机制解的双节面下半球投影图；Ⅱ ：最优断层节面下半球投影；Ⅲ ：两组震源丛最优发震断层的主断层节面；Ⅳ ：主断层节面的P，T轴
Figure 5. Nodal map of main fault identified by stress inversion of focal mechanism solutions of five groups of earthquake sequences
Ⅰ ：Double-nodal lower hemispherical projection of focal mechanism solutions of the earthquake sequence；Ⅱ ：Lower hemispherical projection of optimal fault nodal plane；Ⅲ ：Optimal occurrence of the main fault nodal plane for the two sets of focal clusters；Ⅳ ：The P and T axis of the main fault nodal plane （a） 2008-03-21；（b） 2008-08-21；（c） 2008-09-03；（d） 2011-03-10；（e） 2011-08-09
![]()
图 6 主压应力轴应力场分布模型图
Figure 6. Stress field distribution model diagram of principal compressive stress axis
表 1 构造应力场应力主轴反演结果
Table 1 Inversion results of stress principal axis of tectonic stress field
地震序列主震
发震日期分区 震源机制解
个数σ1 σ2 σ3 应力形因子R 方位角/° 倾角/° 方位角/° 倾角/° 方位角/° 倾角/° 2008-03-21 A区 17 44 3 258 86 135 2 0.78 2008-08-21 B区 36 215 33 40 57 306 2 0.40 2008-09-03 C区 48 34 3 212 87 304 0 0.75 2011-03-10 D区 61 193 15 333 70 99 12 0.57 2011-08-09 E区 23 195 1 294 83 105 7 0.65 
下载: 导出CSV
表 2 迭代应力反演识别出的最优主断层节面
Table 2 Optimal main fault nodal plane identified by iterative stress inversion
地震序列主震
发震日期反演识别的两组主断层节面 地震序列主震
发震日期反演识别的两组主断层节面 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° 2008-03-21 250 89 4 2011-03-10 158 88 161 199 86 −178 223 72 −7 2008-08-21 241 77 −31 2011-08-09 164 85 176 12 73 −151 225 84 3 2008-09-03 187 89 −177 60 88 −3
下载: 导出CSV
-
邓菲,刘杰. 2014. 2008年盈江地震序列的震源参数和震源机制相关系数研究[J]. 地震,34(2):22–34. doi: 10.3969/j.issn.1000-3274.2014.02.003 Deng F,Liu J. 2014. Source parameters and correlation coefficients of focal mechanisms for the 2008 Yingjiang earthquake sequence[J]. Earthquake,34(2):22–34 (in Chinese).
房立华,吴建平,张天中,黄静,王长在,杨婷. 2011. 2011年云南盈江MS5.8地震及其余震序列重定位[J]. 地震学报,33(2):262–267. doi: 10.3969/j.issn.0253-3782.2011.02.013 Fang L H,Wu J P,Zhang T Z,Huang J,Wang C Z,Yang T. 2011. Relocation of mainshock and aftershocks of the 2011 Yingjiang MS5.8 earthquake in Yunnan[J]. Acta Seismologica Sinica,33(2):262–267 (in Chinese).
郭祥云,陈学忠,王生文,王恒信. 2014. 川滇地区中小地震震源机制解及构造应力场的研究[J]. 地震工程学报,36(3):599–607. doi: 10.3969/j.issn.1000-0844.2014.03.0599 Guo X Y,Chen X Z,Wang S W,Wang H X. 2014. Focal mechanism of small and moderate earthquakes and tectonic stress field in Sichuan-Yunnan areas[J]. China Earthquake Engineering Journal,36(3):599–607 (in Chinese).
胡晓辉. 2020. 云南及邻区构造应力场研究[D]. 三河: 防灾科技学院: 45–46. Hu X H. 2020. The Study of Tectonic Stress Field in Yunnan and Its Adjacent Areas[D]. Sanhe: Institute of Disaster Prevention: 45–46 （in Chinese）.
黄小龙,吴中海,赵小艳,吴坤罡,黄小巾,杜锦锦. 2015. 2014年5月云南盈江MS5.6、MS6.1地震发震构造分析[J]. 地球学报,36(6):760–769. Huang X L,Wu Z H,Zhao X Y,Wu K G,Huang X J,Du J J. 2015. Seismogenic structure of 2014 MS5.6 and MS6.1 earthquakes in Yingjiang,Yunnan Province[J]. Acta Geoscientica Sinica,36(6):760–769 (in Chinese).
季建清,钟大赉,张连生. 2000. 滇西南新生代走滑断裂运动学、年代学、及对青藏高原东南部块体运动的意义[J]. 地质科学,35(3):336–349. doi: 10.3321/j.issn:0563-5020.2000.03.009 Ji J Q,Zhong D L,Zhang L S. 2000. Kinematics and dating of cenozoic strike-slip faults in the Tengchong area,West Yunnan:Implications for the block movement in the southeastern Tibet Plateau[J]. Scientia Geologica Sinica,35(3):336–349 (in Chinese).
罗艳, 包丰, 倪四道, 陈颙, 陈棋福, 付虹. 2011. 2008年云南盈江MS5.9地震序列初步研究[C]//中国地球物理学会第二十七届年会论文集. 长沙: 中国科学技术大学出版社: 422. Luo Y, Bao F, Ni S D, Chen Y, Chen Q F, Fu H. 2011. Study on the 2008 MS5.9 earthquake sequence in Yingjiang, Yunnan Province[C]//Proceedings of the 27th Annual Meeting of Chinese Geophysical Society. Changsha: China University of Science and Technology Press: 422 （in Chinese）.
孙尧,吴中海,安美建,龙长兴. 2014. 川滇地区主要活动断裂的活动特征及其近十年的地震活动性[J]. 地震工程学报,36(2):320–330. doi: 10.3969/j.issn.1000-0844.2014.02.0320 Sun Y,Wu Z H,An M J,Long C X. 2014. Activity characteristics of primary active faults in Yunnan-Sichuan area and their seismic activity in the past[J]. China Earthquake Engineering Journal,36(2):320–330 (in Chinese).
万永革. 2012. 根据震源机制求解构造应力场的网格搜索法[J]. 国际地震动态,(6):19. Wan Y G. 2012. The grid search algorithm of tectonic stress tensor based on focal mechanism data[J]. Recent Developments in World Seismology,(6):19 (in Chinese).
谢富仁,苏刚,崔效锋,舒赛兵,赵建涛. 2001. 滇西南地区现代构造应力场分析[J]. 地震学报,23(1):17–23. doi: 10.3321/j.issn:0253-3782.2001.01.003 Xie F R,Su G,Cui X F,Shu S B,Zhao J T. 2001. Modern tectonic stress field in southwestern Yunnan,China[J]. Acta Seismologica Sinica,14(1):17–23 (in Chinese).
徐彦. 2013. 云南地区ML3.0级以上中小地震震源机制解汇编2008—2012[M]. 云南: 云南科技出版社: 168–186. Xu Y. 2013. Decollection of Focal Mechanism of Moderate and Small Earthquakes With ML3.0 or Higher in Yunnan Area （2008−2012）[M]. Yunnan: Yunnan Science and Technology Press: 168–186 （in Chinese）.
张丽娜,韩立波,罗艳. 2016. 2014年5月云南盈江两次中强地震震源参数研究[J]. 地震,36(1):59–68. doi: 10.3969/j.issn.1000-3274.2016.01.007 Zhang L N,Han L B,Luo Y. 2016. Source parameters of May 24,2014 MS5.6 and May 30,2014 MS6.1 earthquakes in Yingjiang,Yunnan Province[J]. Earthquake,36(1):59–68 (in Chinese).
张艳凤,常祖峰,彭永中,张亚宏. 2018. 2014年云南盈江6.1级地震宏观异常及其与构造关联性讨论[J]. 地震研究,41(1):148–156. doi: 10.3969/j.issn.1000-0666.2018.01.019 Zhang Y F,Chang Z F,Peng Y Z,Zhang Y H. 2018. Discuss on macro-anomalies of the Yunnan Yingjiang M6.1 earthquake and its relation of tectonics[J]. Journal of Seismological Research,41(1):148–156 (in Chinese).
赵小艳,韩立波,龙锋. 2012. 2011年盈江MS≥4.0地震序列震源机制解与发震构造研究[J]. 地震研究,35(4):477–484. doi: 10.3969/j.issn.1000-0666.2012.04.006 Zhao X Y,Han L B,Long F. 2012. Focal mechanism solutions and seismogenic structures of Yingjiang MS≥4.0 earthquake sequences in 2011[J]. Journal of Seismological Research,35(4):477–484 (in Chinese).
Gephart J W,Forsyth D W. 1984. An improved method for determining the regional stress tensor using earthquake focal mechanism data:Application to the San Fernando earthquake sequence[J]. J Geophys Res,89(B11):9305–9320. doi: 10.1029/JB089iB11p09305
Hardebeck J L,Michael A J. 2006. Damped regional-scale stress inversions:Methodology and examples for southern California and the Coalinga aftershock sequence[J]. J Geophys Res,111(B11):B11310.
Harris R A. 1998. Introduction to special section:Stress triggers,stress shadows,and implications for seismic hazard[J]. J Geophys Res,103(B10):24347–24358. doi: 10.1029/98JB01576
Jacques A. 2002. Inversion of earthquake focal mechanisms to obtain the seismotectonic stress IV:A new method free of choice among nodal planes[J]. Geophys J Int,150(3):588–609. doi: 10.1046/j.1365-246X.2002.01713.x
Lund B,Slunga R. 1999. Stress tensor inversion using detailed microearthquake information and stability constraints:Application to Őlfus in southwest Iceland[J]. J Geophys Res,104(B7):14947–14964. doi: 10.1029/1999JB900111
Martínez-Garzón P,Kwiatek G,Ickrath M,Bohnhoff M. 2014. MSATSI:A MATLAB package for stress inversion combining solid classic methodology,a new simplified user-handling,and a visualization tool[J]. Seismol Res Lett,85(4):896–904. doi: 10.1785/0220130189
Michael A J. 1984. Determination of stress from slip data:Faults and folds[J]. J Geophys Res,89(B13):11517–11526. doi: 10.1029/JB089iB13p11517
Michael A J. 1987. Use of focal mechanisms to determine stress:A control study[J]. J Geophys Res,92(B1):357–368. doi: 10.1029/JB092iB01p00357
Vavryčuk V,Bouchaala F,Fischer T. 2013. High-resolution fault image from accurate locations and focal mechanisms of the 2008 swarm earthquakes in West Bohemia,Czech Republic[J]. Tectonophysics,590:189–195. doi: 10.1016/j.tecto.2013.01.025
Vavryčuk V. 2014. Iterative joint inversion for stress and fault orientations from focal mechanisms[J]. Geophys J Int,199(1):69–77. doi: 10.1093/gji/ggu224
-
期刊类型引用(3)
1. 高曹珀，王自法，周阳，WANG Jianming. 基于大样本模拟的巨灾损失计算方法. 保险研究. 2023(03): 105-116 . 
百度学术
2. 邵霄怡，王晓青，窦爱霞，袁小祥. 基于蒙特卡洛方法的地震目录模拟及相符性检验——以汾渭地震带为例. 中国地震. 2018(01): 35-47 . 百度学术
3. Shao Xiaoyi，Wang Xiaoqing，Dou Aixia，Yuan Xiaoxiang. Seismic Inventory Simulation and Conformance Test Based on the Monte Carlo Method——A Case Study of the Fenhe-Weihe Belt. Earthquake Research in China. 2018(04): 533-548 . 必应学术
其他类型引用(0)
计量
- 文章访问数: 751
- HTML全文浏览量: 372
- PDF下载量: 69
- 被引次数: 3
