Accuracy estimation of global tide models using continuous gravity observation data in northern China
-
摘要: 为评估全球潮汐模型在我国潮汐改正中的适用性，本文首先对10个重力站2016—2018年的观测数据进行了精度评定，而后基于均方根、和方根、纬度依赖关系以及重力残差等指标对7个全球潮汐模型进行了精度评定。结果表明：10个重力站的一些评价指标达到甚至超越了早期超导重力仪，例如M2波潮汐因子的中误差普遍小于0.000 70，其中最高精度约为0.000 14，5个主要潮波的稳定度均≤0.001 5。在10个观测模型和7个全球潮汐模型中，DDW-NHi和M2001模型考虑了地球扁率的影响，基于这两个模型计算的和方根较其它模型所得的和方根均小，约为0.288×10−8 m/s2。基于最高精度的乌什站数据对Molodensky， DDW-NHi，M2001与观测模型的改正精度的对比显示，DDW-NHi模型改正计算的重力残差（±0.4×10−8—±1.0×10−8 m/s2）不及观测模型（±0.1×10−8—±0.5×10−8 m/s2），但依然优于M2001模型（±0.7×10−8—±1.4×10−8 m/s2），且DDW-NHi模型改正获得的残差比传统的Molodensky模型所得残差（±0.5×10−8—±1.5×10−8 m/s2）小1×10−8—2×10−8 m/s2.
-
关键词:
- 全球潮汐模型 /
- 海潮负荷改正 /
- 重力残差 /
- 和方根 /
- 潮汐因子纬度依赖关系
Abstract: To evaluate the applicability of the global tide models for tide correction in China, this paper firstly assessed the data accuracy of ten gravity observation from 2016 to 2018, and then made the accuracy assessment for the seven global tide model by the evaluation indicators such as the root mean square （RMS）, the root sum square （RSS）, latitude dependence of the gravimetric amplitude factor, and residual gravity. The result shows that some of the evaluation indicators have achieved or even surpassed the accuracy of the early superconducting gravimeters in ten gravity observations. For example, the RMS of the M2 gravimetric amplitude factor was less than 0.000 70, withthe highest RMS about 0.000 14, and the stability of five main tide waves was less than 0.001 5. As for the ten observed and the seven global tide models, the RSS of DDW-NHi and M2001 models with the Earth’s oblateness influence is only about 0.288×10−8 m/s2, which is smaller than others. Comparison of the tide corrected accuracies by Molodensky, DDW-NHi, M2001, and the observed tide models suggests that residual gravity corrected by DDW-NHi （±0.4×10−8—±1.0×10−8 m/s2） is larger than that by observed one （±0.1×10−8—±0.5×10−8 m/s2） for Wushi gravity observatory with the highest tide accuracy, but still smaller than that by M2001 （±0.7×10−8—±1.4×10−8 m/s2）. Furthermore, the residual gravity corrected by DDW-NHi is less about 1×10−8—2×10−8 m/s2 than by the traditional Molodensky model. -
-
![]()
图 1 我国10个重力观测站空间分布示意图
Figure 1. The spatial distribution of ten gravity observatories in China
![]()
图 2 2016—2018年主要潮波的潮汐因子稳定度变化
（a） O1波；（b） M2波；（c） P1波；（d） K1波
Figure 2. Variation of the stability of gravimetric amplitude factor of the main tidal waves from 2016 to 2018
（a） O1 wave；（b） M2 wave；（c） P1 wave；（d） K1 wave
![]()
图 3 O1波，M2波和K1波的潮汐振幅（a）和潮汐因子（b）的纬度依赖关系
Figure 3. The latitude dependence of the gravimetric amplitude （a） and gravimetric amplitude factors （b） of O1，M2 and K1 waves
![]()
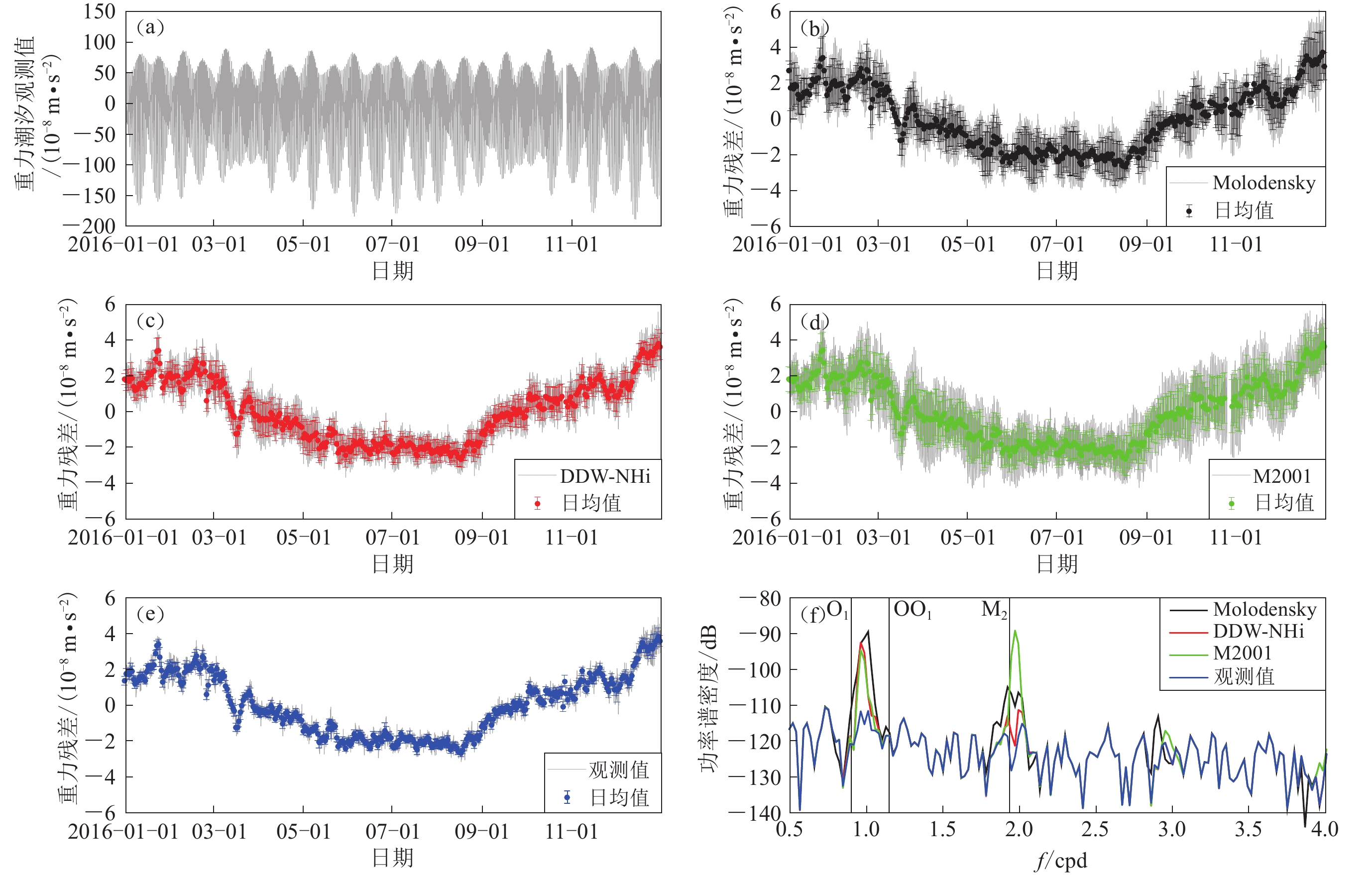
图 4 潮汐模型潮汐改正后的重力残差时间序列及其功率谱密度
（a） 乌什重力站固体潮预处理数据；（b） Molodensky模型潮汐改正的重力残差；（c） DDW-NHi模型潮汐改正的重力残差；（d） M2001模型潮汐改正的重力残差；（e） 观测模型潮汐改正的重力残差；（f） 重力残差的功率谱密度
Figure 4. Residual gravity and power spectral density corrected by several tidal models
（a） The preprocessing gravity data from Wushi observatory；（b） The residual gravity corrected by Molodensky model；（c） The residual gravity corrected by DDW-NHi model；（d） The residual gravity corrected by M2001 model；（e） The residual gravity corrected by observed model；（f） The power spectral density of the residual gravity
![]()
图 5 周日波（a）和半日波（b）的重力残差功率谱密度频段特征
Figure 5. The power spectral density of the residual gravity for diural （a） and semi-diurnal （b） waves
![]()
图 6 海潮负荷改正前后观测的与模型的重力残差振幅比较
图中P代表进行了气压改正；＋N代表进行了Nao.99b海潮负荷改正；＋NC代表进行了Nao.99b和osu.chinasea.2010海潮负荷改正；＋NN代表进行了Nao.99b和naoregional.1999海潮负荷改正
Figure 6. Comparison of the residual gravity amplitude before and after corrected by ocean loading models and global body tide model
P represents the gravimetric amplitude factors corrected by atmospheric pressure；＋N represents those corrected by global ocean model of Nao.99b；＋NC represent the those corrected by the composite ocean model of Nao. 99b and osu.chinasea.2010；＋NN represent those corrected by the composite ocean model of Nao.99b and naoregional.1999
![]()
图 7 海潮改正对潮汐因子的影响
图中P代表进行了气压改正的潮汐因子；DUT10，EOT11a，FES2004，GOT4.7，HAM11a，Nao.99b和TPXO7.2分别代表进行了气压和对应全球海潮模型改正的潮汐因子；DDW-NHi代表了DDW-NHi理论潮汐因子。横坐标台站按经度由东向西排列
Figure 7. Impaction of the gravimetric amplitude factors corrected by seven global ocean models
P represents the gravimetric amplitude factors corrected by atmospheric pressure；DUT10，EOT11a，FES2004，GOT4.7，HAM11a，Nao.99b and TPXO7.2 represent those corrected by atmospheric pressure and corresponding global ocean tide model respectively；DDW-NHi represents those in DDW-NHi. The stations are arranged from east to west according to their longitude
![]()
图 8 格尔木观测站潮汐因子和调和分析中误差随格值系数的变化
（a） M2波；（b） O1波；（c） K1波；（d） P1波；（e） Q1波；（f） 中误差随格值系数的变化
Figure 8. Varaition of gravimetric amplitude factor and RMS of the harmonic analysis with the scale factor for Golmud observatory
（a） M2 wave；（b） O1 wave；（c） K1 wave；（d） P1 wave；（e） Q1 wave；（f） The RMS of the residual gravity
表 1 全球潮汐模型的特征
Table 1 Feature statistics of global body tide models
来源 长周期波 周日波 半日波 1/3日波 地球模型 Molodensky （1961） - 4 1 - 圆球 Warh （1981a，b，c） 1 19 1 0 1066A，PREM-C，C2 Dehant et al （1999） 1 9 1 1 流体静力弹性地球模型 11 9 1 1 非流体非弹性地球模型 Mathews （2001） - 16 - - PREM 
下载: 导出CSV
表 2 7个全球潮汐模型潮汐因子的常数项和纬度依赖项
Table 2 Constant term and latitude-dependent term of the gravimetric amplitude factor in seven global body tide models
全球潮汐模型 O1波 P1波 K1波 Q1波 M2波 ${G_0} $ 
$G_ { \pm }'/10^{-5}$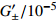 
${G_0} $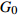 
$G_ { \pm }'/10^{-5}$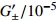 
${G_0} $ 
$G_ { \pm }'/10^{-5}$ 
${G_0} $ 
$G_ { \pm }'/10^{-5}$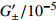 
${G_0} $ 
$G_ { \pm }'/10^{-5}$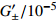 
Molodensky 圆球 1.16 0 1.153 0 1.137 0 1.137 0 1.16 0 1066A 1.152 −600 1.147 −600 1.132 −600 1.152 −600 1.16 −500 Warh PREM-C 1.152 −700 1.147 −700 1.132 −600 1.152 −700 1.16 −500 C2 1.151 −700 1.147 −600 1.132 −600 1.151 −700 1.159 −500 Dehant DDW-He 1.154 24 8 1.147 77 −13 1.147 77 −13 1.132 83 −60 1.160 30 7 DDW-NHi 1.154 24 8 1.149 15 −10 1.134 89 −57 1.154 03 9 1.161 72 10 Mathews M2001 1.154 07 5 1.148 91 5 1.136 1 5 1.154 1 5 - - 注： ${G_0} $ 为潮汐因子的全球常数项，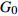
$G_ { \pm }'$ 为纬度依赖项系数，其中M2001模型的
${G_0} $ 为原模型常数项的模，
$G_ { \pm }'$ 为原模型的周期项。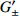
下载: 导出CSV
表 3 2016年重力潮汐观测站基本信息
Table 3 Basic information of the gravity observatories in 2016
序号 台站 省份 台站
类型观测环境
等级台站简介 中误差
/（10−8 m·s−2）1 高台 甘肃 地下室 优秀 位于黑河以北不足2 km处 ±0.637 2 格尔木 青海 山洞 优秀 位于昆仑布尔汉达山北麓山洞中 ±0.706 3 海拉尔 内蒙 山洞 优秀 位于海拉尔盆地与大兴安岭北坡海拉尔河与伊敏河交汇处 ±0.601 4 兰州 甘肃 山洞 优秀 位于兰州东盆地盐场堡以北、白塔山以东、黄河北岸Ⅲ级阶级地的后缘，
距黄河最近距离约1.5 km±0.740 5 牡丹江 黑龙江 山洞 良好 距市区约1.6 km，近年在距离台站500 m处建有成片住宅小区 ±0.718 6 沈阳 辽宁 山洞 良好 位于沈阳市东郊东陵区天柱山西南麓，南距沈抚公路北线约0.4 km ±0.747 7 泰安 山东 山洞 良好 位于泰山南麓正南，0.5 km处有小型水库 ±0.989 8 炭山 宁夏 山洞 良好 位于海原县炭山乡丘陵村，距海原县新区约20 km，台站供电系统时常故障 ±0.891 9 乌加河 内蒙 山洞 优秀 位于内蒙古自治区巴彦淖尔市乌拉特中旗乌加河镇正北1 km处 ±0.838 10 乌什 新疆 山洞 优秀 阿克苏地区乌什县西郊的七女坟旁 ±0.605
下载: 导出CSV
表 4 连续重力观测站的潮汐因子δ和气压导纳值的统计结果
Table 4 The result of gravimetric amplitude factor δ and barometric admittance of gravity observatories
重力站 O1波 P1波 K1波 M2波 S2波 气压导纳/（10−8 m·s−2·hPa−1） δ σ/10−4 δ σ/10−4 δ σ/10−4 δ σ/10−4 δ σ/10−4 数值 中误差 格尔木 1.152 94 4.0 1.145 22 14.3 1.131 84 9.9 1.165 22 1.5 1.165 10 3.4 −0.269 0.015 兰州 1.157 16 4.7 1.148 77 9.0 1.136 50 3.4 1.158 77 2.4 1.160 37 5.4 −0.319 0.011 高台 1.156 37 3.8 1.150 97 6.7 1.137 49 2.5 1.161 62 1.2 1.163 21 2.7 −0.391 0.008 海拉尔 1.155 19 5.9 1.157 16 11.2 1.138 65 4.1 1.167 74 4.2 1.171 67 9.4 −0.371 0.010 牡丹江 1.153 84 4.7 1.151 92 8.4 1.137 44 3.2 1.163 77 3.4 1.167 07 7.5 −0.347 0.009 沈阳 1.153 70 7.3 1.150 00 13.1 1.137 17 4.9 1.159 45 2.8 1.159 77 6.2 −0.356 0.010 泰安 1.158 32 11.3 1.153 09 20.6 1.139 41 7.7 1.155 73 2.4 1.156 20 5.6 −0.288 0.018 炭山 1.154 74 7.8 1.145 53 16.9 1.133 36 6.4 1.161 86 2.4 1.161 45 5.9 −0.312 0.024 乌加河 1.155 54 3.1 1.150 56 5.6 1.137 52 2.1 1.157 09 1.3 1.159 06 3.1 −0.299 0.010 乌什 1.155 14 3.9 1.151 40 7.0 1.137 26 2.6 1.160 97 1.4 1.161 00 3.2 −0.430 0.010 注：δ为潮波的潮汐因子，σ为中误差。
下载: 导出CSV
表 5 乌什重力观测站的潮汐分析结果
Table 5 The tidal analysis results of Wushi gravity observatory
起始频率
/cpd结束频率
/cpd潮波名称 潮汐振幅
/（10−9 m·s−2）潮汐因子 相位滞后/° 数值 中误差 数值 中误差 0.501 37 0.911 39 Q1 58.938 1 1.154 66 0.001 80 −0.097 0.09 0.911 39 0.947 99 O1 307.830 6 1.155 14 0.000 39 0.020 0.019 0.947 99 0.981 85 M1 24.209 7 1.504 93 0.004 20 −0.427 0.160 0.981 86 0.998 63 P1 143.232 9 1.151 40 0.000 70 −0.060 0.035 0.998 63 1.001 37 S1 3.387 2 1.209 77 0.042 58 16.412 2.319 1.001 37 1.004 11 K1 432.929 1 1.137 26 0.000 26 0.007 0.014 1.004 11 1.006 85 ψ1 3.387 1 1.260 70 0.030 07 −0.923 1.368 1.006 85 1.023 62 φ1 6.164 9 1.169 38 0.016 14 −0.622 0.791 1.023 62 1.057 49 J1 24.208 8 1.153 00 0.004 61 −0.174 0.229 1.057 49 1.470 24 OO1 13.246 6 1.162 69 0.011 38 0.117 0.561 1.470 24 1.880 26 2N2 13.001 1 1.161 73 0.003 27 0.201 0.161 1.880 27 1.914 13 N2 81.411 6 1.159 33 0.000 71 −0.046 0.035 1.914 13 1.950 42 M2 425.214 3 1.160 97 0.000 14 0.013 0.007 1.950 42 1.984 28 L2 12.018 8 1.157 81 0.006 06 −0.428 0.300 1.984 28 2.002 74 S2 197.832 1 1.161 00 0.000 32 −0.289 0.020 2.002 74 2.451 94 K2 53.780 9 1.158 76 0.001 54 −0.137 0.076 2.451 94 7.000 00 M3M6 6.287 4 1.073 14 0.006 61 0.109 0.353
下载: 导出CSV
表 6 各型重力仪潮汐观测精度和稳定度分析
Table 6 Accuracy and stability analysis of tidal observatory for different gravimeters
重力仪
类型数据时段 M2波潮汐因子
中误差中误差
/（10−8 m·s−2）导纳中误差
/（10−8 m·s−2·hPa−1）稳定度 来源 LRC 1973—1990 0.002 00—0.005 00 - - - Melchior和de Becher （1983） GEO 1971—1990 0.001 00—0.002 00 - - - GWR 1975—1988 0.000 08 - - - LRC 1983—1986 ≤0.005 00 - - 0.005 0 毛慧琴等（1989） GS 1989—1993 0.000 30—0.003 00 - - - 魏望生和喻节林（1995） DZW 0.000 80—0.004 00 - - - LRC 0.000 40—0.002 00 - - - GEO 0.001 00—0.005 00 - - - T，CT，CD 1989—2000 - ±0.05—±0.70 ±0.000 4—0.003 0 0.001 5 Ducarme et al （2002） ASK - - ±0.010 0 - LRC 2000—2001 0.000 51 ±0.20 ±0.022 0 - 孙和平等（2002） OSG 0.000 06 ±0.02 ±0.002 0 - T，CT，CD 1997—2001 0.000 70 - ±0.000 4—0.003 0 0.001 0 Xu et al （2004） OSG 2009—2010 0.000 04 ±1.10—±1.40 ±0.000 5 - 韦进等（2012）
下载: 导出CSV
表 7 7个全球潮汐模型计算所得重力残差的均方根RMS及和方根RSS
Table 7 RMS and RSS of the residual gravity corrected by seven global body tide models
潮汐模型 地球模型 RMS/（10−8 m·s−2） RSS/（10−8 m·s−2） M2波 K1波 O1波 P1波 Q1波 Tamura
潮波表郗钦文
潮波表Molodensky 均质圆球 0.143 9 0.168 7 0.173 4 0.064 8 0.047 8 0.292 8 0.291 2 Warh 1066A 0.190 9 0.179 8 0.169 3 0.068 9 0.039 9 0.322 1 0.322 0 PREM-C 0.190 9 0.179 8 0.169 4 0.069 3 0.040 0 0.322 3 0.320 6 C2 0.199 9 0.179 8 0.171 2 0.068 9 0.039 9 0.328 5 0.329 0 DDW DDW-He 0.143 6 0.227 5 0.167 1 0.066 6 0.053 7 0.328 0 0.328 1 DDW-NHi 0.144 5 0.171 3 0.167 1 0.065 2 0.040 2 0.289 8 0.289 6 Mathews M2001 0.144 5 0.168 3 0.167 2 0.065 2 0.040 2 0.288 1 0.287 9
下载: 导出CSV
表 8 两个全球潮汐模型与观测站的潮汐因子的相对误差
Table 8 The relative errors of the gravimetric amplitude factors between DDW-NHi and M2001 models and the observatories
台站 M2波潮汐因子相对误差 O1波潮汐因子相对误差 P1波潮汐因子相对误差 K1波潮汐因子相对误差 RMS/（10−8 m·s−2） DDW-NHi M2001 DDW-NHi M2001 DDW-NHi M2001 DDW-NHi M2001 DDW-NHi M2001 格尔木 0.251 3% 0.251 3% 0.178 2% 0.150 4% 0.253 3% 0.247 4% 0.259 5% 0.459 4% 0.120 6 0.141 0 高台 0.015 2% 0.015 2% 0.224 4% 0.253 1% 0.187 8% 0.189 1% 0.312 9% 0.094 1% 0.087 5 0.068 3 海拉尔 0.015 3% 0.495 8% 0.062 1% 0.093 9% 0.815 2% 0.800 9% 0.574 1% 0.290 9% 0.223 8 0.198 0 兰州 0.015 4% 0.211 4% 0.354 1% 0.381 8% 0.269 4% 0.275 8% 0.291 5% 0.093 8% 0.114 6 0.105 1 牡丹江 0.015 5% 0.200 8% 0.188 0% 0.157 6% 0.582 2% 0.575 4% 0.244 1% 0.008 6% 0.227 8 0.220 6 乌什 0.015 6% 0.236 3% 0.025 6% 0.003 9% 0.168 3% 0.165 9% 0.246 3% 0.011 9% 0.107 8 0.095 5
下载: 导出CSV
-
李大炜,李建成,金涛勇,胡敏章. 2012. 利用验潮站资料评估全球海潮模型的精度[J]. 大地测量与地球动力学,32(4):106–110. Li D W,Li J C,Jin T Y,Hu M Z. 2012. Accuracy estimation of recent global ocean tide models using tide gauge data[J]. Journal of Geodesy and Geodynamics,32(4):106–110 (in Chinese).
刘子维,李辉,韦进,郝洪涛,吴云龙. 2011. 利用M2潮波振幅因子精密测定gPhone弹簧重力仪的标定因子[J]. 大地测量与地球动力学,31(5):146–150. Liu Z W,Li H,Wei J,Hao H T,Wu Y L. 2011. Accurate determination of calibration factor of gPhone spring gravimeters by using M2 tidal wave amplitude factor[J]. Journal of Geodesy and Geodynamics,31(5):146–150 (in Chinese).
毛慧琴,许厚泽,宋兴黎,陈振邦. 1989. 中国东西重力潮汐剖面[J]. 地球物理学报,32(1):62–69. doi: 10.3321/j.issn:0001-5733.1989.01.006 Mao H Q,Hus H T,Song X L,Chen Z B. 1989. East-west gravity tidal profile of China[J]. Acta Geophysica Sinica,32(1):62–69 (in Chinese).
孙和平,许厚泽,徐建桥,柳林涛. 2000. 重力场的潮汐变化观测及其研究[J]. 地球科学进展,15(1):53–57. doi: 10.3321/j.issn:1001-8166.2000.01.008 Sun H P,Xu H T,Xu J Q,Liu L T. 2000. Observation and study of the tidal variation in gravity field[J]. Advance in Earth Sciences,15(1):53–57 (in Chinese).
孙和平,陈晓东,刘明,周百力. 2002. LCR-ET20弹簧型潮汐重力仪观测结果的分析和比较[J]. 地震学报,24(5):510–515. doi: 10.3321/j.issn:0253-3782.2002.05.008 Sun H P,Chen X D,Liu M,Zhou B L. 2002. Analysis and comparison of the tidal gravity observations obtained with LCR-ET20 spring gravimeter[J]. Acta Seismologica Sinica,24(5):510–515 (in Chinese).
韦进,李辉,刘子维,康开轩,郝洪涛. 2012. 武汉九峰地震台超导重力仪观测分析研究[J]. 地球物理学报,55(6):1894–1902. doi: 10.6038/j.issn.0001-5733.2012.06.010 Wei J,Li H,Liu Z W,Kang K X,Hao H T. 2012. Observation of superconducting gravimeter at Jiufeng seismic station[J]. Chinese Journal of Geophysics,55(6):1894–1902 (in Chinese).
魏望生,喻节林. 1995. 中国大陆重力潮汐参数及其特征研究[J]. 地壳形变与地震,15(4):77–85. Wei W S,Yu J L. 1995. Study on the gravity tide parameters and their characteristics in the mainland of China[J]. Crustal Deformation and Earthquake,15(4):77–85 (in Chinese).
郗钦文,侯天航. 1987. 新的引潮位完全展开[J]. 地球物理学报,30(4):349–362. Xi Q W,Hou T H. 1987. A new complete development of the tide-generating potential for the epoch J2000.0[J]. Acta Geophysica Sinica,30(4):349–362 (in Chinese).
张锐,韦进,刘子维,李辉,郝洪涛. 2011. 用SGC053超导重力仪观测资料对gPh058重力仪格值的精密测定[J]. 大地测量与地球动力学,31(5):151–155. Zhang R,Wei J,Liu Z W,Li H,Hao H T. 2011. Accurate determination of scale value of gPh058 gravimeter by use of observations with SGC053 superconducting gravimeter[J]. Journal of Geodesy and Geodynamics,31(5):151–155 (in Chinese).
周江存,徐建桥,孙和平. 2009. 中国大陆精密重力潮汐改正模型[J]. 地球物理学报,52(6):1474–1482. doi: 10.3969/j.issn.0001-5733.2009.06.008 Zhou J C,Xu J Q,Sun H P. 2009. Accurate correction models for tidal gravity in Chinese continent[J]. Chinese Journal of Geophysics,52(6):1474–1482 (in Chinese).
Dehant V,Ducarme B. 1987. Comparison between the theoretical and observed tidal gravimetric factors[J]. Phys Earth Planet Inter,49(3/4):192–212.
Dehant V,Defraigne P,Wahr J M. 1999. Tides for a convective Earth[J]. J Geophys Res,104(B1):1035–1058. doi: 10.1029/1998JB900051
Ducarme B,Sun H P,Xu J Q. 2002. New investigation of tidal gravity results from the GGP network[J]. Bull Inf Marees Terrestres,136:10761–10776.
Francis O,Niebauer T M,Sasagawa G,Klopping F,Gschwind J. 1998. Calibration of a superconducting gravimeter by comparison with an absolute gravimeter FG5 in Boulder[J]. Geophys Res Lett,25(7):1075–1078. doi: 10.1029/98GL00712
Hábel B,Meurers B. 2014. A new tidal analysis of superconducting gravity observations in western and central Europe[J]. Contribut Geophys Geodesy,44(1):1–24. doi: 10.2478/congeo-2014-0001
Love A E H. 1909. The yielding of the Earth to disturbing forces[J]. Mon Not R astr Soc,69(551):476.
Mathews P M. 2001. Love numbers and gravimetric factor for diurnal tides[J]. J Geodetic Soc Jpn,46(4):231–236.
Melchior P,de Becker M. 1983. A discussion of world-wide measurements of tidal gravity with respect to oceanic interactions,lithosphere heterogeneities,Earth’s flattening and inertial forces[J]. Phys Earth Planet Inter,31(1):27–53. doi: 10.1016/0031-9201(83)90064-X
Melchior P. 1994. A new data bank for tidal gravity measurements (DB 92)[J]. Phys Earth Planet Inter,82(2):125–155. doi: 10.1016/0031-9201(94)90085-X
Molodensky M S. 1961. The theory of nutation and diurnal Earth tides[J]. Communs Obs Roy Belg,288:25–56.
Tamura Y. 1987. A harmonic development of the tide-generating potential[J]. Bull Inf Marees Terrestres,99:6817–6855.
Wahr J M. 1981a. Body tides on an elliptical,rotating,elastic and oceanless earth[J]. Geophys J R astr Soc,64(3):677–703. doi: 10.1111/j.1365-246X.1981.tb02690.x
Wahr J M. 1981b. A normal mode expansion for the forced response of a rotating earth[J]. Geophys J R astr Soc,64(3):651–675. doi: 10.1111/j.1365-246X.1981.tb02689.x
Wahr J M. 1981c. The forced nutations of an elliptical,rotating,elastic and oceanless earth[J]. Geophys J R astr Soc,64(3):705–727. doi: 10.1111/j.1365-246X.1981.tb02691.x
Xu J Q,Sun H P,Ducarme B. 2004. A global experimental model for gravity tides of the Earth[J]. J Geodyn,38(3/5):293–306.
-
期刊类型引用(5)
1. 田思留，李风懿，鲁楠楠，刘涛，阳光，赵霞，李杰. 姑咱台DZW重力仪和燕子沟台gPhone重力仪对比观测分析. 四川地震. 2025(02): 27-32 . 
百度学术
2. 赵亚博，胡敏章，韦进，江颖，张晓彤，刘子维. 以潮汐模型为约束的gPhone重力仪格值系数标定方法改进. 大地测量与地球动力学. 2023(08): 826-831 . 百度学术
3. 韦进，胡敏章，韩宇飞，鲁小飞，江颖. 福建省重力台网对米娜台风激发的微震信号源定位. 武汉大学学报(信息科学版). 2022(06): 955-963 . 百度学术
4. 韦进，胡敏章，申重阳，王嘉沛. gPhone重力仪绝对标定方法研究. 华中科技大学学报(自然科学版). 2022(09): 41-47 . 百度学术
5. 韦进，郝洪涛，韩宇飞，胡敏章，江颖，刘子维. 基于连续重力台观测的玛多M_S7.4地震的同震重力变化特征. 地震地质. 2021(04): 984-998 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 947
- HTML全文浏览量: 420
- PDF下载量: 74
- 被引次数: 6
