Impact of the tsunami excited by the 2011 MW9.0 Japan earthquake on seismic ambient noises
-
摘要: 基于北美沿岸和内陆地震台站的连续地震波形记录，并结合沿岸台站附近布设的DART系统记录的海底压力数据以及预测潮汐数据，利用时频分析和极化分析方法对2011年3月11日日本东北部海域MW9.0大地震所激发的海啸对地震背景噪声所产生的影响予以深入分析。结果显示：海啸对高频噪声（1.3—1.5 Hz）以及短周期双频微地动噪声（0.18—0.4 Hz）的影响较小，但海啸显著增强了长周期双频微地动（0.1—0.15 Hz）、单频微地动（0.05—0.08 Hz）以及地球背景自由振荡（0.004—0.007 Hz）的振幅，且随着噪声频率的降低，这种振幅增强的影响更明显，影响的持续时间也更长；海啸到达近岸时，对附近台站的各频段噪声均有影响，成为各频段噪声的主控能量来源，且其位置在后续过程中会随时间变化。这表明海啸对噪声特征的影响与海啸传播特性有关，即海啸在传播过程中因受水深、海底地形以及近岸地形的反射、衍射等的影响，能量聚集区域随时间而变化，并非均匀地传播到海岸， 从而导致了不同频带噪声主极化方向随时间的变化。
-
关键词:
- 海啸 /
- 2011年日本MW9.0地震 /
- 地震背景噪声 /
- 地球背景自由振荡 /
- 微地动
Abstract: The MW9.0 earthquake on March 11, 2011 occurred in the northeastern sea of Japan triggered a catastrophic tsunami, which had significant influences on the seismic ambient noises with ocean-lithosphere coupling. This study uses the continuous data recorded by seismic stations along the coast and inland of North America, combined with the seafloor pressure data recorded by the DART system nearby, as well as the predicted tidal data to analyze the impact of this tsunami on the seismic ambient noises by using time-frequency analysis and polarization analysis methods. The results show that this tsunami had little impact on the high-frequency noise （1.3−1.5 Hz） and short-period double-frequency microseisms （0.18−0.4 Hz）, while it significantly enhanced the amplitudes of long-period double-frequency microseisms （0.1−0.15 Hz）, single-frequency microseisms （0.05−0.08 Hz）, as well as the Earth’s background free oscillations （0.004−0.007 Hz）. Moreover, as the frequency of the ambient noise decreases, the amplitude enhancement becomes more pronounced and lasts longer. When the tsunami reaches the shore, it has an impact on the ambient noise of coastal stations nearby for all three frequency-bands of Earth’s background free oscillations, microseisms, and high-frequency noise and becomes the main energy source of seismic ambient noises at all three frequency bands. And the position of the dominant tsunami sources changes with time. All above-mentioned suggests that the influence of tsunami on seismic ambient noise is related to the propagation characteristics of tsunami, that is, due to the influence of water depth, reflections and diffractions of seafloor and inshore topography, the energy accumulation area changes with time, and the energy does not propagate uniformly to the coast, resulting in the changes of dominant polarization direction of seismic ambient noise in different frequency bands with time. By cross-disciplines of seismology and oceanography, this study is of significance for advancing studies on the coupling mechanism of ocean-lithosphere, identifying the characteristics of tsunami waves from the perspective of seismology, as well as exploring new tsunami warning mechanisms. -
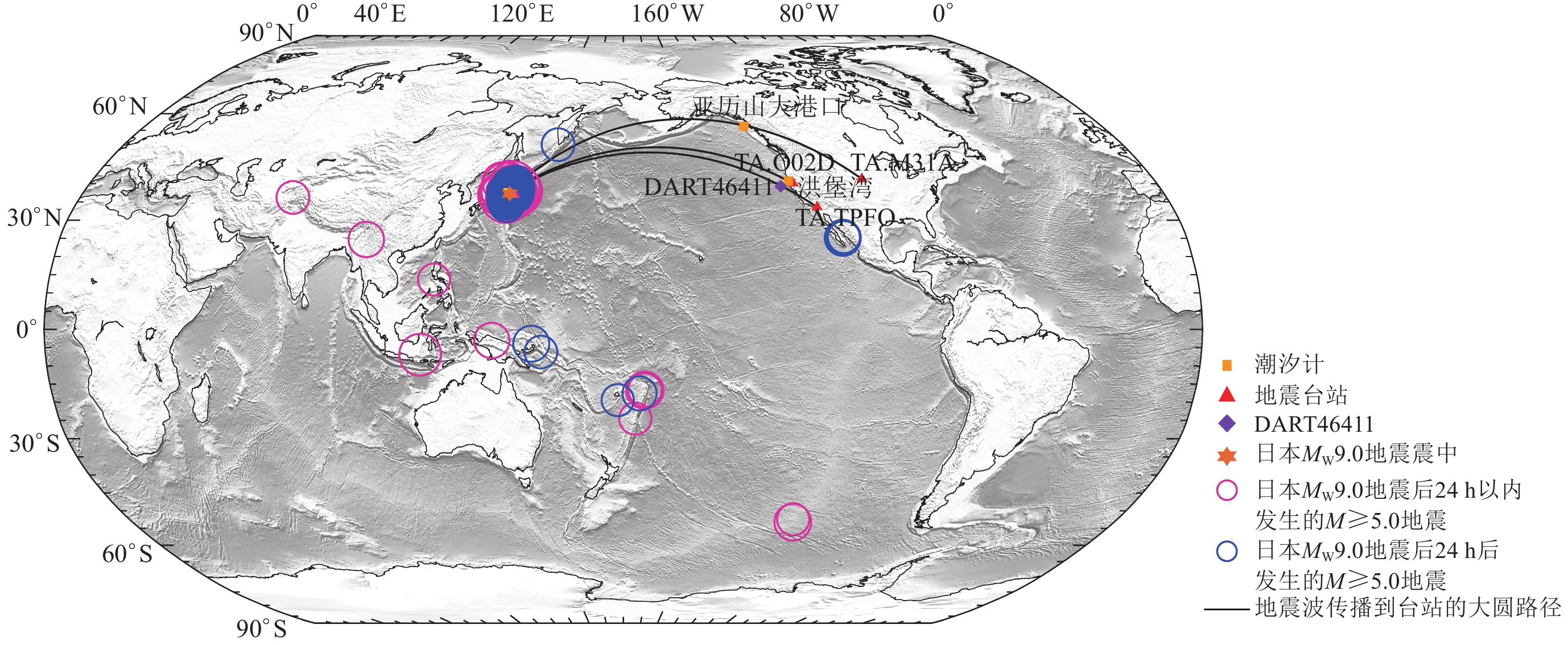
图 1 本文所用的地震台站、DART站、潮汐计以及2011年3月10日至3月15日期间全球M≥5.0地震震中位置的空间分布图（圆圈大小表示地震震级的相对大小）
Figure 1. The spatial distributions of seismic stations，DART station and tide meters used in this study as well as the global M≥5.0 earthquake epicenter locations from March 10 to 15，2011 （The circle size indicates the relative magnitude of the earthquake）
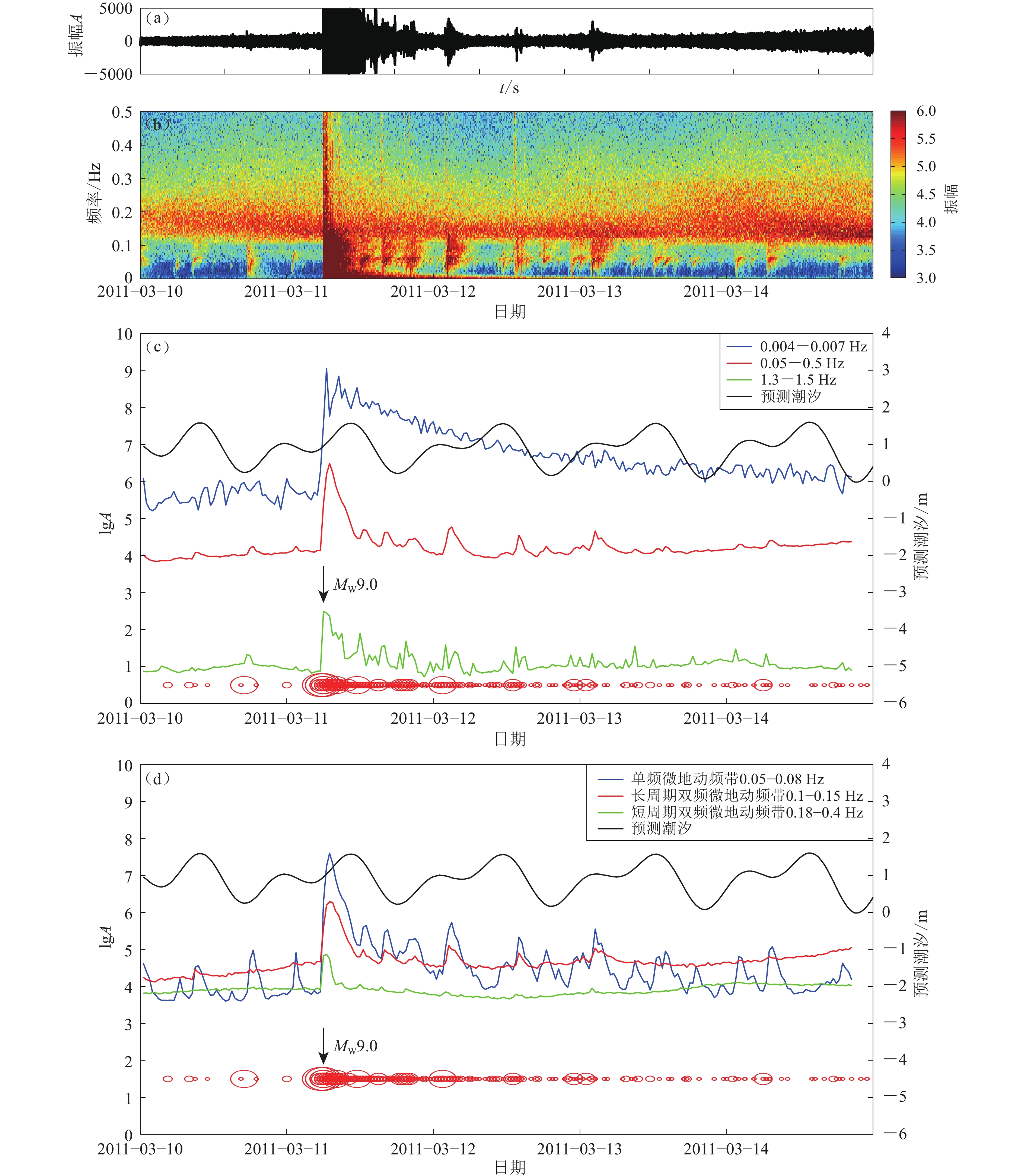
图 2 2011年3月10日至15日TA.O02D台站垂直分量的时频分析结果
（a） 波形图；（b） 时频图；（c） 不同频段的半小时平均振幅A曲线；（d） 微地动频带内不同频段的半小时平均振幅A曲线。图（c）和（d）中红色圆圈表示M≥5地震的发生时刻和震级大小。地震目录引自美国国家地震信息中心（USGS，2020）
Figure 2. Time-frequency analysis results of the vertical component of the station TA.O02D from March 10 to 15，2011
（a） Waveform diagram；（b） Time-frequency diagram；（c） Half-hour average amplitude curves in different frequency bands；（d） Half-hour average amplitude curves of different frequency bands in microseisms. In Figs. （c） and （d），red circles indicate the time and magnitude of M≥5 earthquakes. Earthquake catalogue comes from USGS （2020）
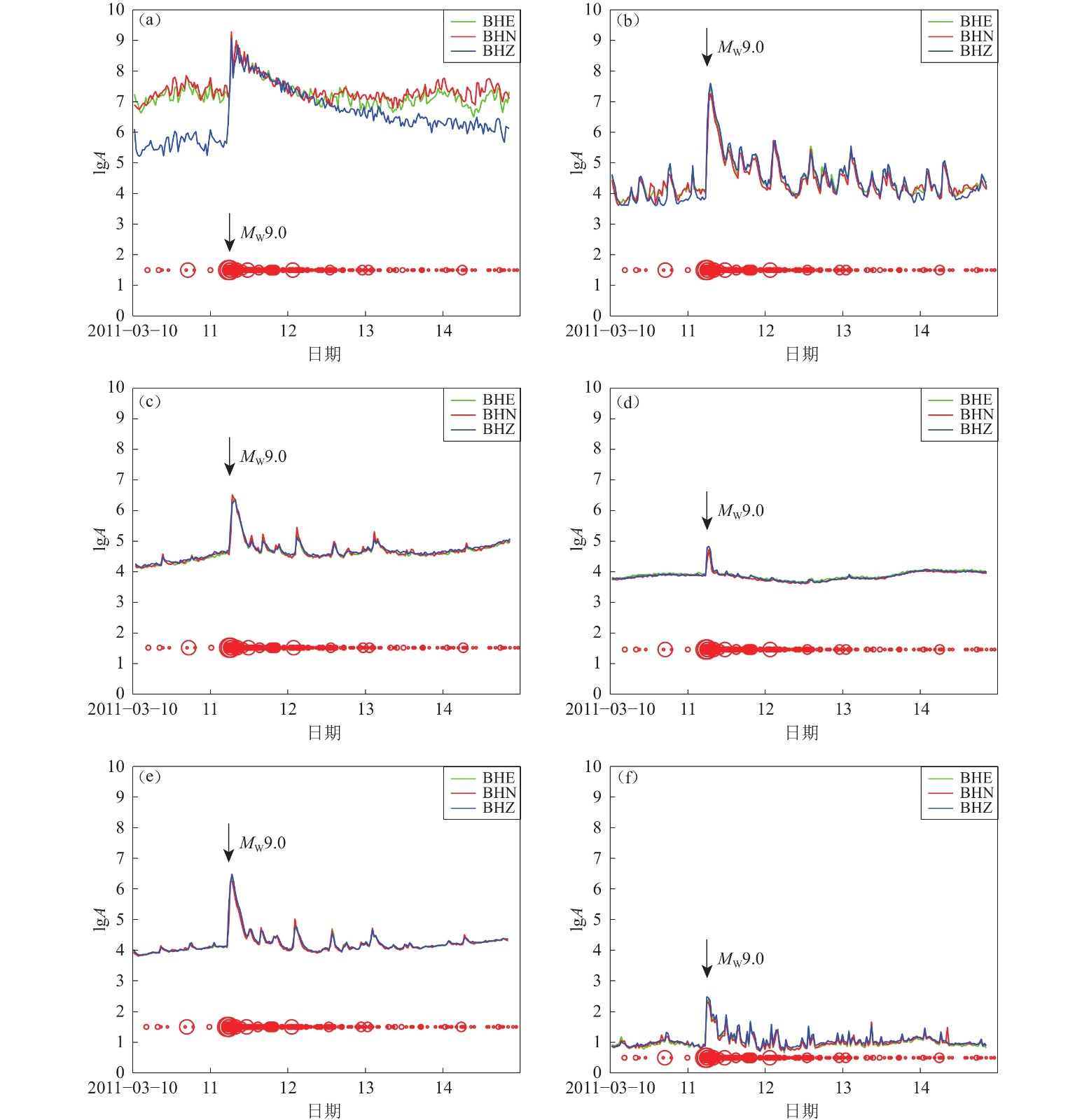
图 3 2011年3月10日至15日TA.O02D台站三分量地震连续波形记录在不同频带的半小时平均振幅A的变化曲线
（a） 地球背景自由振荡频带（0.004—0.007 Hz）；（b） 单频微地动频带（0.05—0.08 Hz）；（c） 长周期双频微地动频带（0.1—0.15 Hz）；（d） 短周期双频微地动频带（0.18—0.4 Hz）；（e） 微地动频带（0.05—0.5 Hz）；（f） 高频噪声频带（1.3—1.5 Hz）。红色圆圈的意思与图2相同。
Figure 3. The variation curves of half-hour average amplitude A of the three-component seismic continuous waveform records for the station TA.O02D for different frequency bands from March 10 to 15，2011
（a） The Earth’s background free oscillation frenquency band （0.004−0.007 Hz）；（b） Single-frequency microseism frenquency band （0.05−0.08 Hz）；（c） Long-period double-frequency microseism frenquency band （0.1−0.15 Hz）；（d） Short-period double-frequency microseism frenquency band （0.18−0.4 Hz）；（e） Microseism frenquency band （0.05−0.5 Hz）；（f） The high-frequency noise （1.3−1.5 Hz）. The meanings of the red circles are the same as in Fig. 2
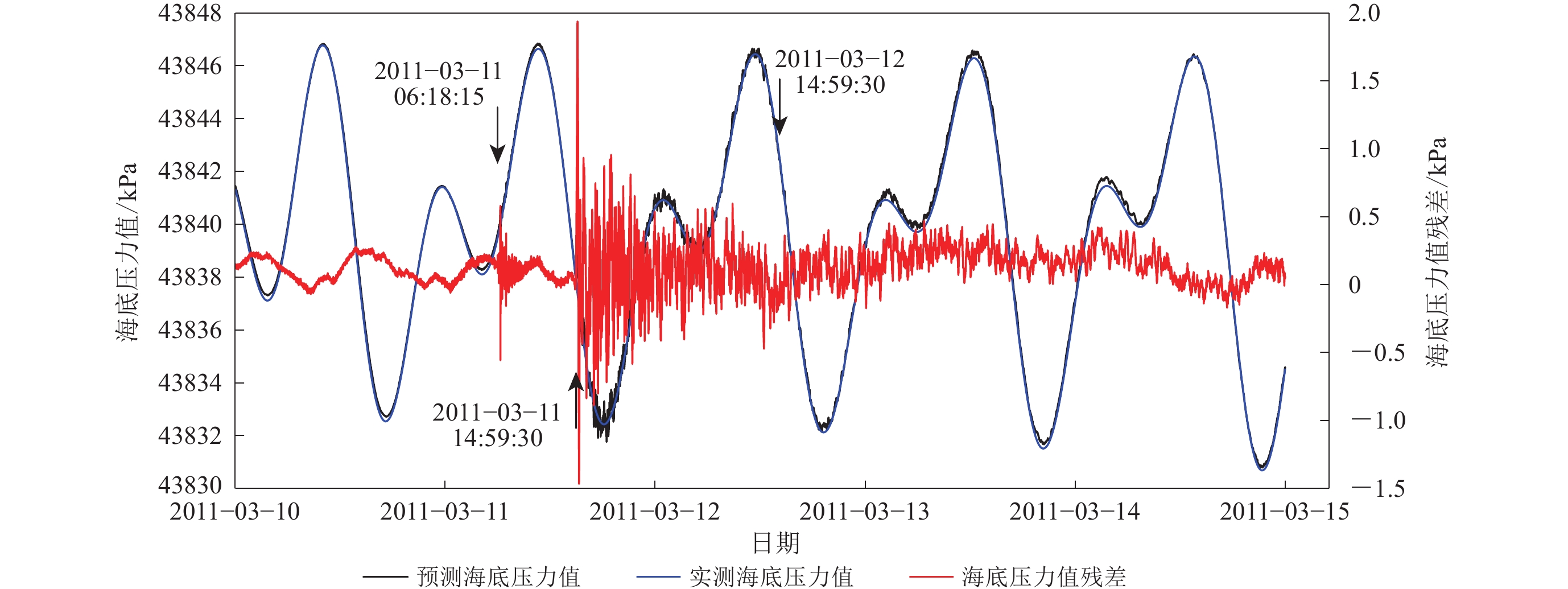
图 4 日本MW9.0地震前后DART46411台站记录到的2011年3月10日至15日的海底压力值
箭头指示台站记录的海啸频段的海浪实测与预测高度残差幅值超过3 cm阈值进入快速汇报模式（提供海啸预警信息）的时刻
Figure 4. The seafloor pressure values recorded by the station DART46411 during the 2011 Japanese tsunami from March 10 to 15，2011
The arrows indicate the moments when the residuals between measured and predicted waves heightin the tsunami band recorded by the station exceeds the 3 cm threshold and enters the rapid reporting mode （which provides tsunami warning information）
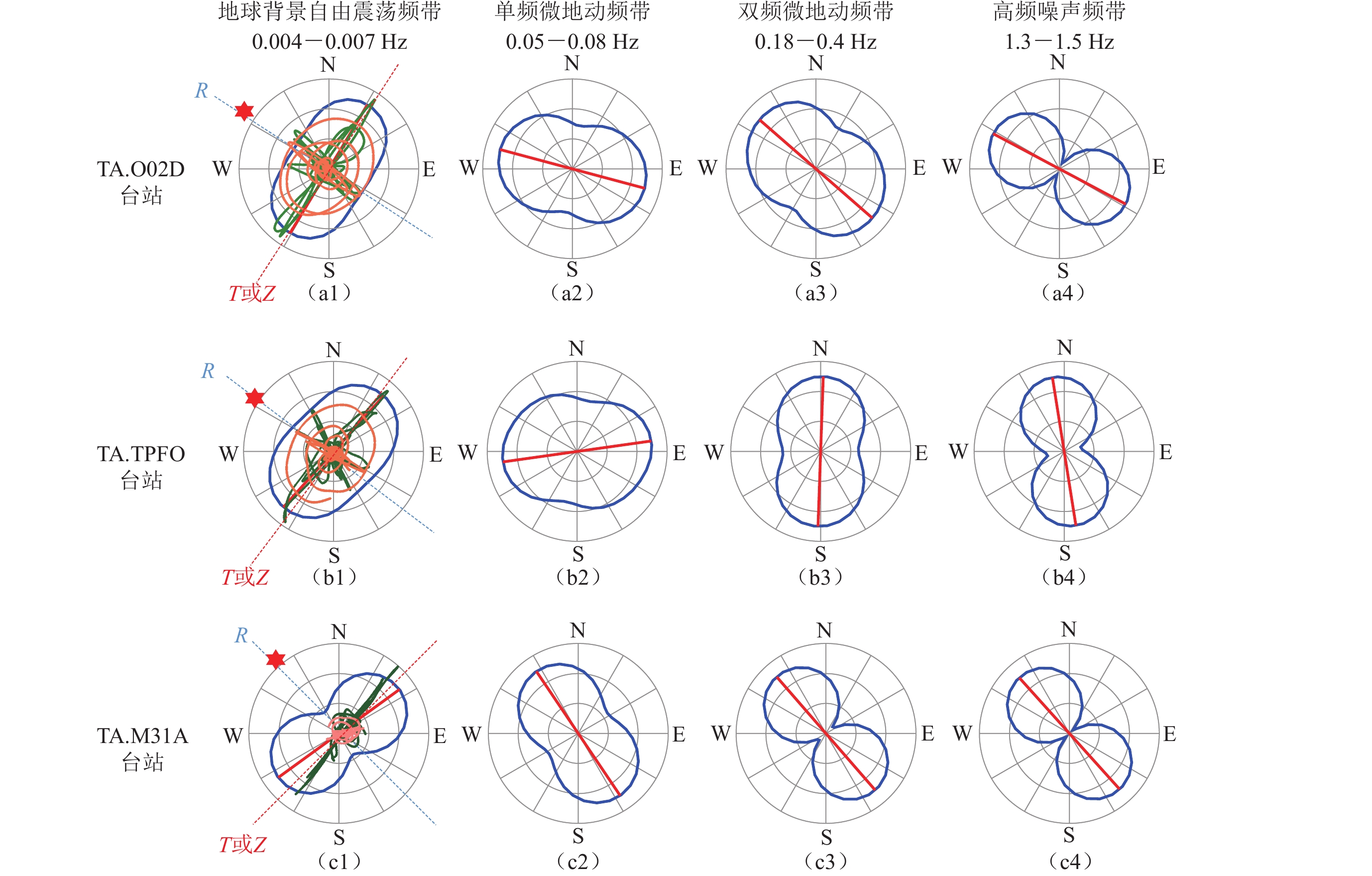
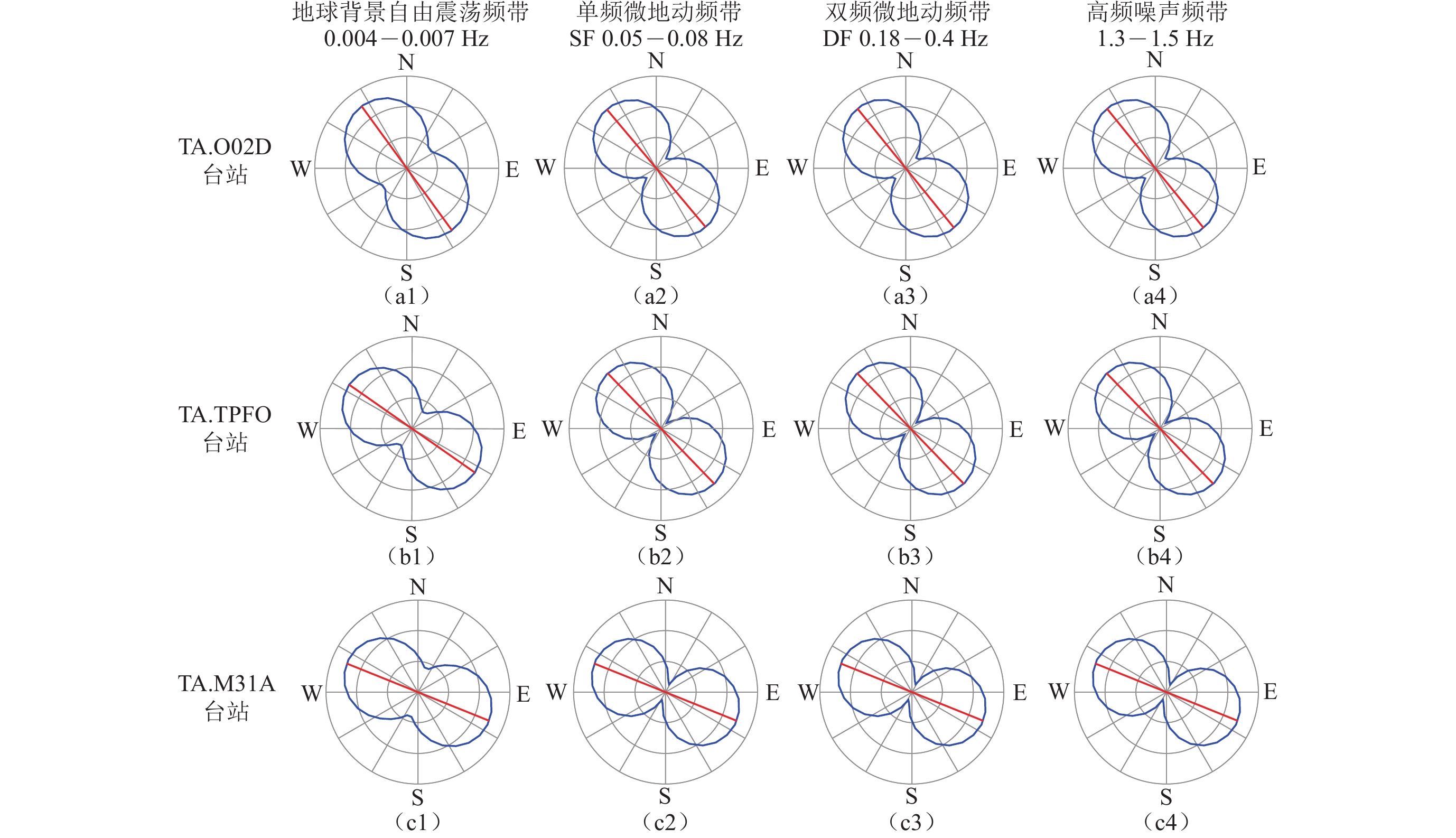
图 5 台站TA.O02D （a）、TA.TPFO （b）和TA.M31A （c）的连续地震波形记录在3月11日6:00—6:30时窗内的极化分析结果
红色直线表示在该时间窗口内各频段内连续地震波形记录的主极化方向，蓝色实线表示各频段内连续地震波形记录在各方位上的振幅。第一列中，红色星形表示对应时间窗口内M≥5.0余震相对地震台站的大圆路径方位，绿色曲线表示该时间窗口内连续地震波形记录的R-T水平面内的质点振动图，橙色曲线表示R-Z竖直面内的质点振动图，蓝色虚线表示质点振动图中的R分量方向，红色虚线对R-T和R-Z质点振动图来说分别代表T分量和垂直分量Z的方向
Figure 5. Polarization analysis results of the continuous seismic waveforms of the stations TA.O02D （a）， TA.TPFO （b） and TA.M31A （c） recorded from 6:00 to 6:30 on March 11
Red lines indicate the predominant polarization direction of the continuous seismic waveforms recorded in each frequency band，and blue solid lines indicate the amplitude of the continuous seismic waveform recorded in each azimuth in each frequency band. In the first column subfigures，the red stars indicate the position of the great circle path of the M≥5 aftershocks relative to the seismic stations in the corresponding time window，green curves indicates the particle vibration diagram in the R-T horizontal plane，orange curves indicate the particle vibration diagram in the R-Z vertical plane. Blue dotted lines indicate the direction of the component R in the particle vibration diagrams，red dotted lines represent the direction of the component T and the vertical component Z of the R-T and R-Z particle vibration diagrams，respectively
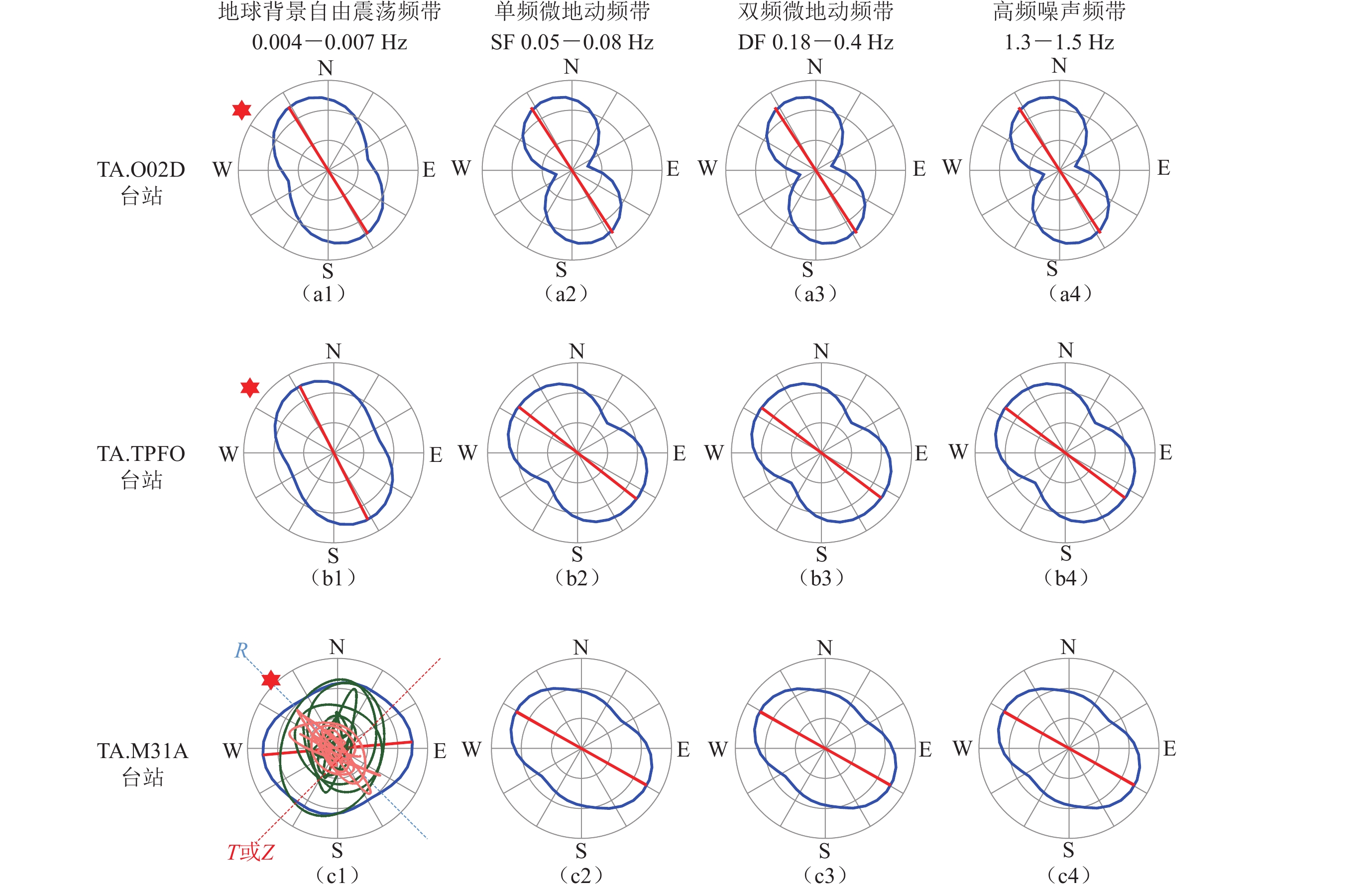
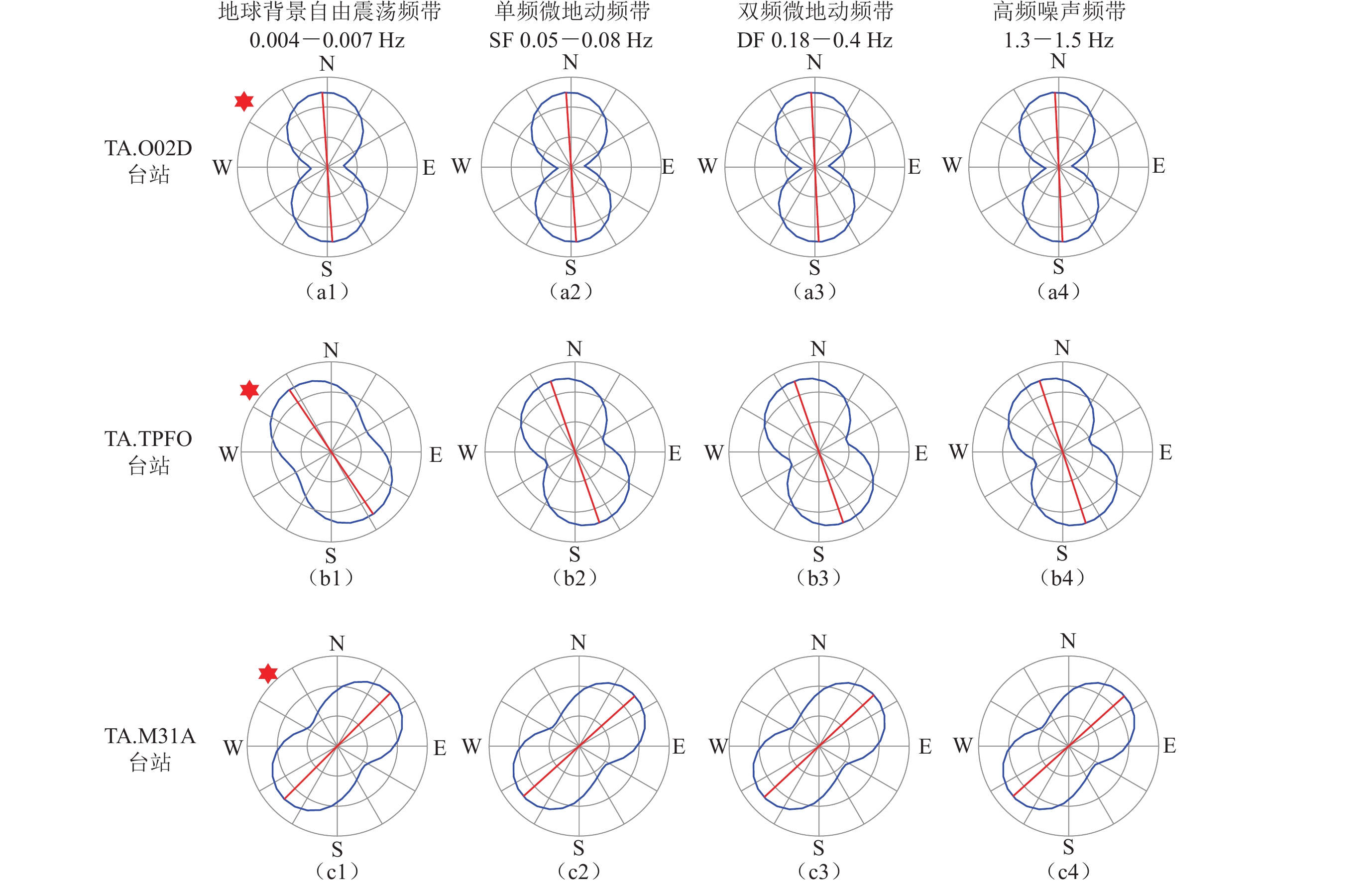
图 6 台站TA.O02D （a），TA.TPFO （b）和TA.M31A （c）的连续地震波形记录在时间窗3月11日15:00—15:30内的极化分析结果（图注说明同图5）
Figure 6. Polarization analysis results of the continuous seismic waveforms of the stations TA.O02D （a），TA.TPFO （b） and TA.M31A （c） recorded from 15:00 to 15:30 on March 11 （The illustrations are the same as Fig. 5）
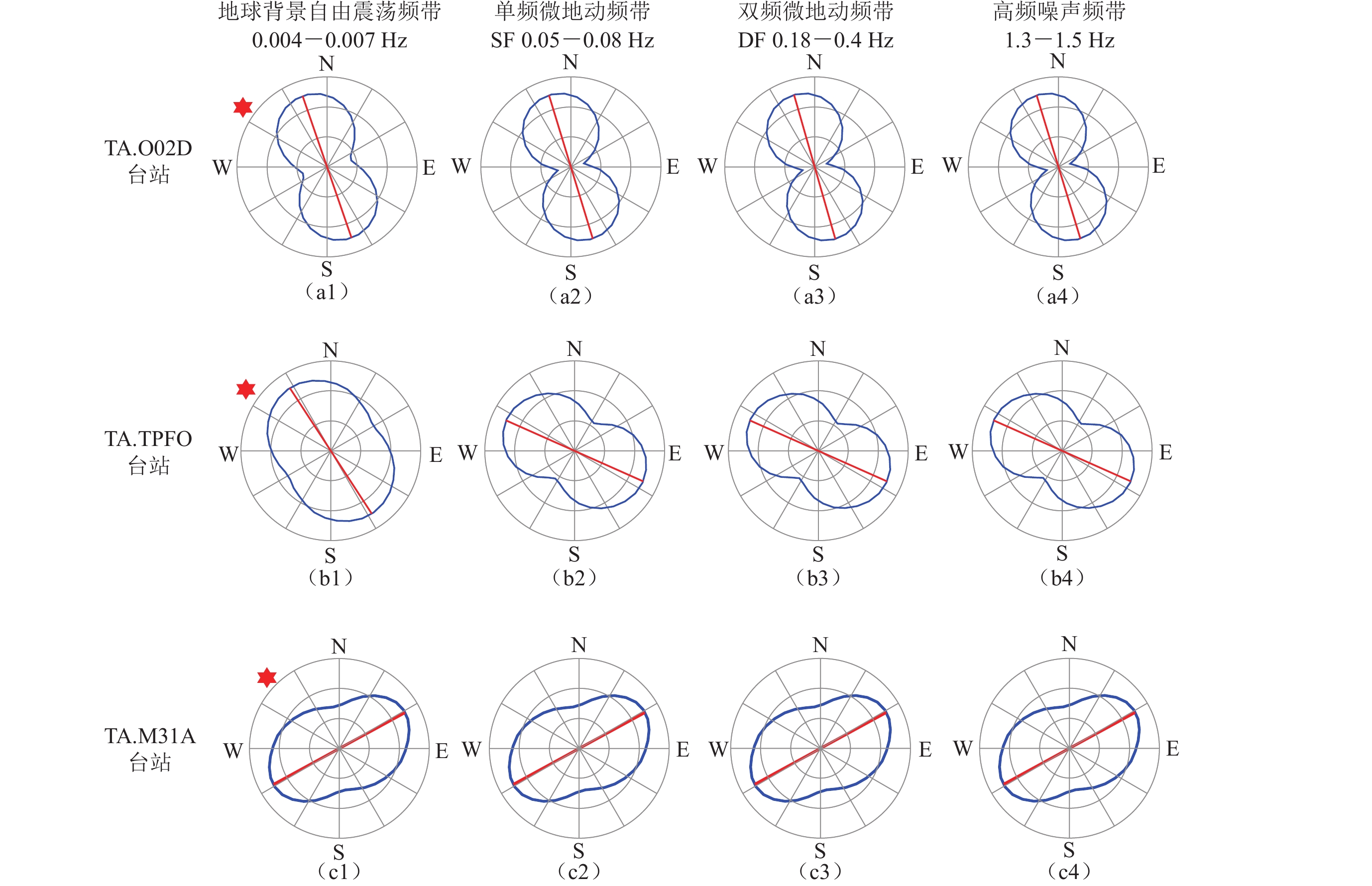
图 7 台站TA.O02D （a），TA.TPFO （b）和TA.M31A （c）的连续地震波形记录在时间窗3月11日15:30—16:00内的极化分析结果（图注说明同图5）
Figure 7. Polarization analysis results of the continuous seismic waveform of the stations TA.O02D （a），TA.TPFO （b） and TA.M31A （c） recorded from 15:30 to 16:00 on March 11，2011 （The illustrations are the same as Fig.5）
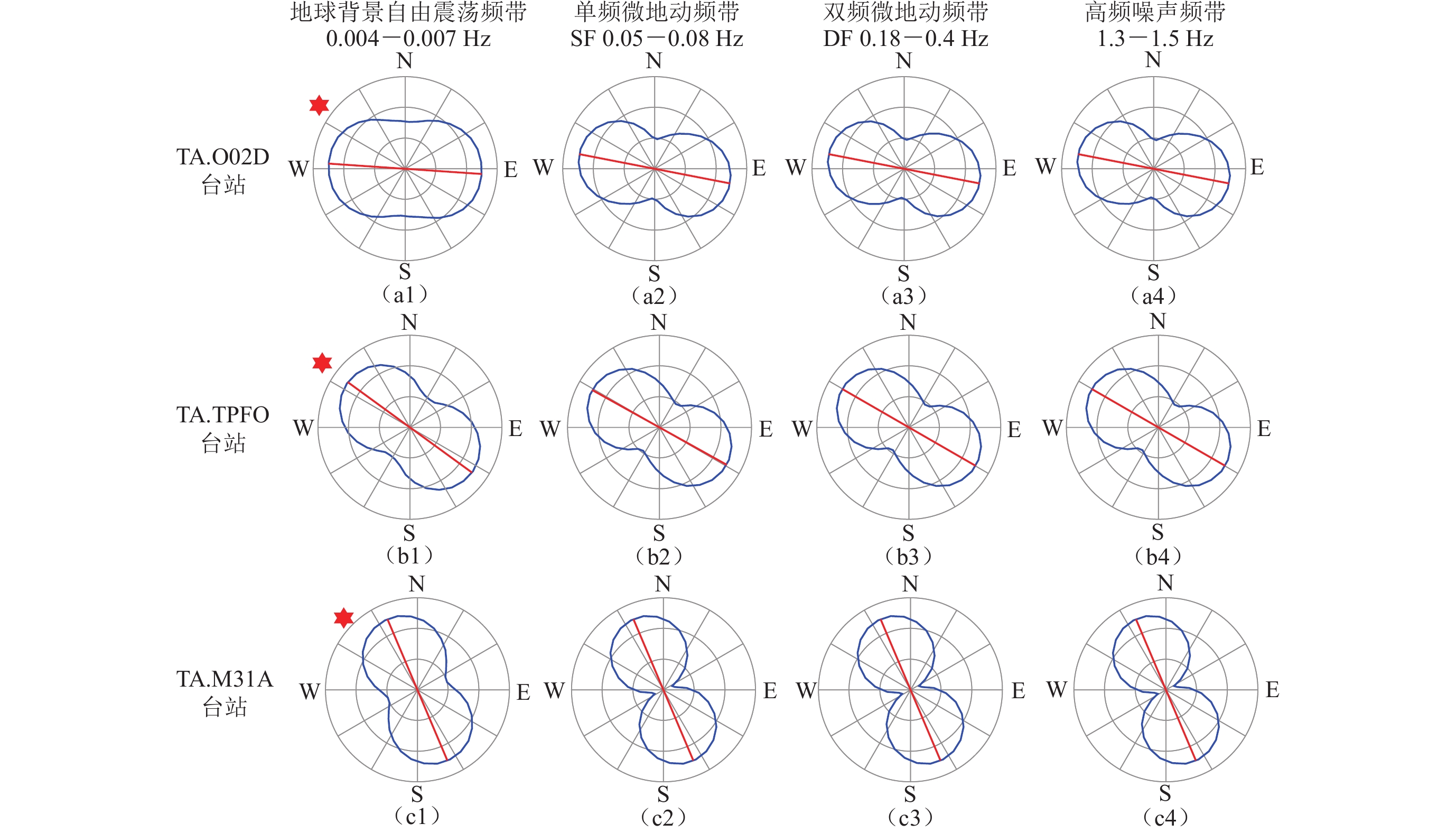
图 9 台站TA.O02D （a），TA.TPFO （b）和TA.M31A （c）的连续地震波形记录在时间窗3月11日22:00—22:30内的极化分析结果（该时窗内无M≥5.0地震发生，图注说明同图5）
Figure 9. Polarization analysis results of the continuous seismic waveforms of the stations TA.O02D （a），TA.TPFO （b） and TA.M31A （c） recorded from 22:00 to 22:30 on March 11 （Note：No M≥5.0 earthquake occurred in the time window，and the illustrations are the same as Fig. 5）
图 10 台站TA.O02D （a），TA.TPFO （b）和TA.M31A （c）的连续地震波形记录在时间窗3月12日15:00—15:30内的极化分析结果（图注说明同图5）
Figure 10. Polarization analysis results of the continuous seismic waveforms of the stations TA.O02D （a），TA.TPFO （b） and TA.M31A （c） recorded from 15:00 to 15:30 on March 12，2011 （Illustrations are the same as Fig.5）
-
[1] 叶琳,于福江,吴玮. 2005. 我国海啸灾害及预警现状与建议[J]. 海洋预报,22(增刊1):147–157. doi: 10.3969/j.issn.1003-0239.2005.z1.021 [2] Ye L,Yu F J,Wu W. 2005. The disaster and warning of tsunami in China and the suggestion in future[J]. Marine Forecasts,22(Z1):147–157 (in Chinese). doi: 10.3969/j.issn.1003-0239.2005.z1.021（inChinese） [3] Benioff H,Harrison J C,LaCoste L,Munk W H,Slichter L B. 1959. Searching for the Earth’s free oscillations[J]. J Geophys Res,64(9):1334–1337. doi: 10.1029/JZ064i009p01334 [4] Bensen G D,Ritzwoller M H,Barmin M P,Levshin A L,Lin F,Moschetti M P,Shapiro N M,Yang Y. 2007. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J]. Geophys J Int,169(3):1239–1260. doi: 10.1111/j.1365-246X.2007.03374.x [5] Bromirski P D,Duennebier F K,Stephen R A. 2005. Mid-ocean microseisms[J]. Geochem Geophys Geosyst,6(4):Q04009. doi: 10.1029/2004gc000768 [6] Bromirski P D. 2009. Earth vibrations[J]. Science,324(5930):1026–1027. [7] Bromirski P D,Gerstoft P. 2009. Dominant source regions of the Earth’s “hum” are coastal[J]. Geophys Res Lett,36(13):L13303. doi: 10.1029/2009gl038903 [8] Cicconi G,Dagnino I,Eva C. 1983. Comparative spectra of microseisms and swell in the Ligurian Sea[J]. Dev Solid Earth Geophys,15:237–241. doi: 10.1016/B978-0-444-99662-6.50051-4 [9] Ekström G. 2001. Time domain analysis of Earth’s long-period background seismic radiation[J]. J Geophys Res:Solid Earth,106(B11):26483–26493. doi: 10.1029/2000JB000086 [10] Fine I V,Kulikov E A,Cherniawsky J Y. 2013. Japan’s 2011 tsunami:Characteristics of wave propagation from observations and numerical modelling[J]. Pure Appl Geophys,170(6/7/8):1295–1307. [11] Fujii Y,Satake K. 2007. Tsunami source of the 2004 Sumatra-Andaman earthquake inferred from tide gauge and satellite data[J]. Bull Seismol Soc Am,97(1A):S192–S207. doi: 10.1785/0120050613 [12] Fujii Y,Satake K. 2008. Tsunami sources of the November 2006 and January 2007 great Kuril earthquakes[J]. Bull Seismol Soc Am,98(3):1559–1571. doi: 10.1785/0120070221 [13] Fujii Y,Satake K,Sakai S,Shinohara M,Kanazawa T. 2011. Tsunami source of the 2011 off the Pacific coast of Tohoku earthquake[J]. Earth Planets Space,63(7):815–820. [14] Fukao Y,Nishida K,Suda N,Nawa K,Kobayashi N. 2002. A theory of the Earth’s background free oscillations[J]. J Geophys Res:Solid Earth,107(B9):2206. doi: 10.1029/2001jb000153 [15] Gerstoft P,Shearer P M,Harmon N,Zhang J. 2008. Global P,PP,and PKP wave microseisms observed from distant storms[J]. Geophys Res Lett,35(23):L23306. doi: 10.1029/2008gl036111 [16] Gilbert F,MacDonald G. 1959. Free oscillations of the Earth[J]. J Geophys Res,64:1103–1104. [17] Hasselmann K. 1963. A statistical analysis of the generation of microseisms[J]. Rev Geophys,1(2):177–210. doi: 10.1029/RG001i002p00177 [18] Heidarzadeh M,Satake K. 2013. Waveform and spectral analyses of the 2011 Japan tsunami records on tide gauge and DART stations across the Pacific Ocean[J]. Pure Appl Geophys,170(6/7/8):1275–1293. doi: 10.1007/s00024-012-0558-5 [19] Kobayashi N,Nishida K. 1998. Continuous excitation of planetary free oscillations by atmospheric disturbances[J]. Nature,395(6700):357–360. doi: 10.1038/26427 [20] Koper K D,Burlacu R. 2015. The fine structure of double-frequency microseisms recorded by seismometers in North America[J]. J Geophys Res:Solid Earth,120(3):1677–1691. doi: 10.1002/2014jb011820 [21] Lacoss R T,Kelly E J,Toksöz M N. 1969. Estimation of seismic noise structure using arrays[J]. Geophysics,34(1):21–38. doi: 10.1190/1.1439995 [22] Longuet-Higgins M S. 1950. A theory of the origin of microseisms[J]. Philos Trans R Soc Lond A:Math Phys Eng Sci,243(857):1–35. doi: 10.1098/rsta.1950.0012 [23] Longuet-Higgins M S,Ursell F. 1948. Sea waves and microseisms[J]. Nature,162(4122):700. doi: 10.1038/162700a0 [24] McCreery C S,Duennebier F K,Sutton G H. 1993. Correlation of deep ocean noise (0.4−30 Hz) with wind,and the Holu Spectrum:A worldwide constant[J]. J Acoust Soc Am,93(5):2639–2648. doi: 10.1121/1.405838 [25] Mungov G,Eblé M,Bouchard R. 2013. DART® tsunameter retrospective and real-time data:A reflection on 10 years of processing in support of tsunami research and operations[J]. Pure Appl Geophys,170(9/10):1369–1384. [26] Munk W H. 1963. Some comments regarding diffusion and absorption of tsunamis[C]//Proceedings of the Tsunami Meeting, X Pacific Science Congress. Paris: IUGG Monogr: 31–41. [27] Nishida K,Kobayashi N. 1999. Statistical features of Earth’s continuous free oscillations[J]. J Geophys Res:Solid Earth,104(B12):28741–28750. doi: 10.1029/1999jb900286 [28] Nishida K,Kobayashi N,Fukao Y. 2000. Resonant oscillations between the solid earth and the atmosphere[J]. Science,287(5461):2244–2246. doi: 10.1126/science.287.5461.2244 [29] Obrebski M J,Ardhuin F,Stutzmann E,Schimmel M. 2012. How moderate sea states can generate loud seismic noise in the deep ocean[J]. Geophys Res Lett,39(11):L11601. [30] Pugh D, Woodworth P. 2014. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes[M]. Cambridge: Cambridge University Press: 60–96. [31] Rhie J,Romanowicz B. 2004. Excitation of Earth’s continuous free oscillations by atmosphere-ocean-seafloor coupling[J]. Nature,431(7008):552–556. doi: 10.1038/nature02942 [32] Rhie J,Romanowicz B. 2006. A study of the relation between ocean storms and the Earth’s hum[J]. Geochem Geophys Geosyst,7(10):Q10004. doi: 10.1029/2006gc001274 [33] Satake K,Fujii Y,Harada T,Namegaya Y. 2013. Time and space distribution of coseismic slip of the 2011 Tohoku earthquake as inferred from tsunami waveform data[J]. Bull Seismol Soc Am,103(2B):1473–1492. doi: 10.1785/0120120122 [34] Shapiro S L,Carlson L E,Astin J A,Freedman B. 2006. Mechanisms of mindfulness[J]. J Clin Psychol,62(3):373–386. doi: 10.1002/jclp.20237 [35] Shevchenko G,Ivelskaya T,Loskutov A. 2014. Characteristics of the 2011 great Tohoku tsunami on the Russian far east coast:Deep-water and coastal observations[J]. Pure Appl Geophys,171(12):3329–3350. doi: 10.1007/s00024-013-0727-1 [36] Stehly L,Campillo M,Shapiro N M. 2006. A study of the seismic noise from its long-range correlation properties[J]. J Geophys Res:Solid Earth,111(B10):B10306. doi: 10.1029/2005jb004237 [37] Suda N,Nawa K,Fukao Y. 1998. Earth’s background free oscillations[J]. Science,279(5359):2089–2091. doi: 10.1126/science.279.5359.2089 [38] Sun T H Z,Xue M,Le K P,Zhang Y W,Xu H P. 2013. Signatures of ocean storms on seismic records in South China Sea and East China Sea[J]. Mar Geophys Res,34(3/4):431–448. doi: 10.1007/s11001-013-9204-6 [39] Tanimoto T,Um J. 1999. Cause of continuous oscillations of the Earth[J]. J Geophys Res:Solid Earth,104(B12):28723–28739. doi: 10.1029/1999jb900252 [40] Tanimoto T. 2005. The oceanic excitation hypothesis for the continuous oscillations of the Earth[J]. Geophys J Int,160(1):276–288. doi: 10.1111/j.1365-246X.2004.02484.x [41] Tanimoto T,Ishimaru S,Alvizuri C. 2006. Seasonality in particle motion of microseisms[J]. Geophys J Int,166(1):253–266. doi: 10.1111/j.1365-246X.2006.02931.x [42] Tanimoto T. 2007. Excitation of microseisms[J]. Geophys Res Lett,34(5):L05308. doi: 10.1029/2006gl029046 [43] Titov V,Rabinovich A B,Mofjeld H O,Thomson R E,Gonzalez F I. 2005. The global reach of the 26 December 2004 Sumatra tsunami[J]. Science,309(5743):2045–2048. doi: 10.1126/science.1114576 [44] Toksöz M N,Lacoss R T. 1968. Microseisms:Mode structure and sources[J]. Science,159(3817):872–873. doi: 10.1126/science.159.3817.872 [45] USGS. 2020. Search earthquake catalog[EB/OL]. [2020-03-12]. https://earthquake.usgs.gov/earthquakes/search/. [46] Watada S, Masters G. 2001. Oceanic excitation of the continuous oscillations of the Earth[J]. Eos Trans AGU, 82: SS2A-062082. [47] Webb S C. 2007. The Earth’s ‘hum’ is driven by ocean waves over the continental shelves[J]. Nature,445(7129):754–756. doi: 10.1038/nature05536 [48] Xiao H,Xue M,Yang T,Liu C G,Hua Q F,Xia S H,Huang H B,Le B M,Yu Y Q,Huo D,Pan M H,Li L,Gao J Y. 2018. The characteristics of microseisms in South China Sea:Results from a combined data set of OBSs,broadband land seismic stations,and a global wave height model[J]. J Geophys Res:Solid Earth,123(5):3923–3942. doi: 10.1029/2017jb015291 [49] Ye L L,Lay T,Kanamori H. 2013. Ground shaking and seismic source spectra for large earthquakes around the megathrust fault offshore of northeastern Honshu,Japan[J]. Bull Seismol Soc Am,103(2B):1221–1241. doi: 10.1785/0120120115 [50] Zhang J,Gerstoft P,Shearer P M. 2009. High-frequency P-wave seismic noise driven by ocean winds[J]. Geophys Res Lett,36(9):L09302. doi: 10.1029/2009gl037761 [51] Zhang J,Gerstoft P,Bromirski P D. 2010a. Pelagic and coastal sources of P-wave microseisms:Generation under tropical cyclones[J]. Geophys Res Lett,37(15):L15301. doi: 10.1029/2010gl044288 [52] Zhang J,Gerstoft P,Shearer P M. 2010b. Resolving P-wave travel-time anomalies using seismic array observations of oceanic storms[J]. Earth Planet Sci Lett,292(3/4):419–427. doi: 10.1016/j.jpgl.2010.02.014 -
下载:
查看大图
计量
- 文章访问数: 442
- HTML全文浏览量: 242
- PDF下载量: 25
- 被引次数: 0