The development in seismic application research of VLF/LF radio waves
-
摘要: 甚低频/低频人工源电波作为一种主动源发射的通讯导航信号,因其长距离波导传播的特性在地-电离层观测及应用中表现出极大的优势。本文总结了二十世纪末以来基于甚低频/低频(VLF/LF)电波观测技术及其数据分析方法、典型震例及统计研究成果、圈层耦合机理等方面的研究进展,并通过探讨其应用成果的快速积累及前兆扰动起源等研究难点,展望了未来在我国多种地基和卫星电磁配合下的综合立体体系建设以及该技术可能发挥的最大贡献。Abstract: Radio waves from very low frequency and low frequency (VLF/LF) transmitters, as an active signal for communication and navigation purpose, show great advantages in ionospheric monitoring and application research with their long-distance propagation feature in the waveguide between surface and lower ionosphere. This paper summarized the developments in detecting technology of VLF/LF radio waves, their data analysis methods, case study and statistical research, coupling processes and channels in lithosphere-atmosphere-ionosphere. On the basis of the significant achievements of this technology in earthquake application, and the researches in the origin of big disturbances in VLF/LF observations, the future development plan has been considered to build up a stereo-monitoring system in China by combining our long-history ground-based network and new satellite platform in electromagnetic field, to fully use of this technology in earthquake research.
-
引言
我国是一个地震多发的国家,尤其西部地区地震不断,且我国西部地形起伏多变,多高山峡谷。大量的强震动记录和震害调查表明,相较于平坦地形,复杂不规则地形对地震动影响更大(张建毅等,2012;郭明珠等,2013)。研究地形效应最直观、最有效的方法是实际场地强震动观测及进行实地震害调查和实测数据的分析整理。但强震动观测受制于小概率地震事件,在科学研究和应用上存在一定的局限性。基于此,学者们开展了解析研究和数值模拟来研究地形效应。解析法主要针对简单模型,如圆弧形(Trifunac,1972)、椭圆形(Wong,1982)、U形(Gao et al,2012)及V形(Zhang et al,2012)地形,通过建立简化力学模型并利用波函数展开法进行求解,从本质上解释不规则地形对地震动的散射问题,同时也能为数值模拟精确度的验证提供依据;而数值模拟对复杂地形的研究更具普适性,可弥补解析法在求解复杂地形时的不足,是目前研究地震动在局部场地中的传播及散射的主要技术手段,以有限差分法和有限元法为代表。Ning等(2018)基于有限差分法提出波场分离方法,模拟瑞雷波在二维河谷地形上的传播;李平等(2018)采用二维显式有限差分法研究梯形河谷场地深宽比、河谷坡角、覆盖层厚度及输入地震动强度对场地地震动的影响,并探究了各因素的影响程度;Jahromi和Karkhaneh (2019)用ABAQUS有限元软件研究了不规则地形之间的相互作用对地震响应的影响;孙纬宇等(2019)基于黏弹性边界结合有限元法,研究了SV波入射角度和河谷斜坡坡度对河谷地形地震动放大系数分布特征的影响。为了使数值模拟的结果更精确可靠,要准确地模拟真实场地,科学合理地对其设置人工边界。目前使用的局部人工边界主要有透射边界、黏性边界和黏弹性边界。其中黏弹性边界克服了黏性边界引起的低频漂移问题,能吸收边界上散射波的能量,较好地模拟无限地基的弹性恢复能力和辐射阻尼效应,在一些大型有限元软件中广泛应用(孙纬宇等,2016;马笙杰等,2020)。梁建文等(2014)采用黏弹性边界和等效结点力输入方法,对层状场地中三维凹陷地形进行地震响应分析;Chen等(2015)通过黏弹性人工边界条件,进行二维精细化非线性有限元建模,研究二维复合地形场地的地震效应特征;章小龙等(2017)运用结合黏弹性人工边界的显式有限元法,通过三维转二维的简化方法实现了SV波垂直入射下复杂三维地形地震反应的数值模拟。
地震动在河谷地形中的传播是一个极其复杂的过程,会对跨河谷结构产生较大的不利影响,所以除了从时域角度分析,还应就其频谱特性作进一步研究。王国新等(2013)通过对实际台阵记录的分析,发现地震动相干性随深度的增加而降低;Zerva和Stephenson (2011)以功率谱密度和相干性为评估指标探讨了实际冲积河谷场地的地震动特性;Imtiaz等(2018)通过滞后相干性,研究了场地几何不规则性对地震动的影响。目前,关于从时域和频域角度综合分析三维河谷地形对地震动影响的研究尚不充分,仍需作进一步研究。
本文基于西部某桥梁工程场地,利用ABAQUS有限元软件建立三维河谷地形,拟采用黏弹性人工边界结合隐式动力有限元法,进行动力响应分析,继而通过频谱分析,从时域和频域角度分别探讨河谷地形对地震动的影响,以期为开展河谷场地上桥梁三维地震反应分析提供非一致地震动输入,并进行三维河谷地形分析,以便确定因河谷地形产生的横桥向地震动。
1. 计算模型及计算方法
1.1 河谷场地模型及入射地震动
本文研究对象为西部地区一河谷地形,该地形属于半无限空间数值求解问题,通过人工边界的引入将其转化为有限域求解问题,形成几何尺寸为280 m×50 m×120 m的有限计算区域,剖面几何尺寸如图1所示。在此基础上,基于有限元计算精度要求并结合数值分析截止频率,确定六面体有限单元的几何尺寸为2 m×2 m×2 m,继而对分析区域进行有限单元离散,并建立三维有限元分析模型。之后通过动力有限元数值分析方法建立关于内节点的常微分方程组,并利用ABAQUS分析软件求解器实现其数值积分,其数值积分为隐式、非条件稳定的。假定该河谷场地为一均质且各向同性的弹性体,其密度为2 100 kg/m3,泊松比为0.35,弹性模量为860 MPa,剪切波速为390 m/s2。在河谷地形表面设置15个测点(图1),其中测点3与4,测点4与8,测点8与12,测点12与13之间的水平距离皆为30 m。
入射地震动选用一宽0.2 s、持时1 s的近似脉冲,其位移时程曲线及傅里叶谱如图2所示,截止频率约为12 Hz,有限元计算时间步长取0.002 s。地震动从底部基岩处垂直入射,通过自由场从人工边界面输入,沿河谷地形水平x向振动。
1.2 三维黏弹性人工边界
在三维动力有限元分析中,为了消除人工边界的影响,在底边界和四周侧边界采用黏弹性人工边界条件模拟散射场自人工边界向计算区域外的辐射效应,实质是在人工截断边界上设置一系列并联的线性弹簧和黏滞阻尼器,如图3所示,其参数由围岩材料决定,具体计算公式(马笙杰等,2020)为:
$$ {K_{{\text{BN}}}} = {\alpha _{\text{N}}}\frac{G}{R},{C_{{\text{BN}}}}= \rho {C_{\text{P}}} \text{,} $$ (1) $$ {K_{{\text{BT}}}} = {\alpha _{\text{T}}}\frac{G}{R},{C_{{\text{BT}}}} = \rho {C_{\text{S}}} \text{,} $$ (2) 式中:KBN和KBT分别为法向和切向弹簧的刚度系数;CBN和CBT分别为法向和切向阻尼器的阻尼系数;$ {\alpha _{\text{N}}} $和$ {\alpha _{\text{T}}} $为修正系数,本文考虑三维黏弹性边界情况,取$ {\alpha _{\text{N}}} $=1.33,$ {\alpha _{\text{T}}} $=0.67;R为波源至人工边界点的距离;ρ为介质密度,G为介质的剪切模量,CP和CS分别为P波和S波波速。
1.3 地震动输入
刘晶波和吕彦东(1998)将地震动转化为等效节点力来实现地震动输入,根据力的平衡方程可得到在模型边界点上需要施加的等效荷载,计算公式为:
$$ {F_{\text{B}}} ( t ) = {\sigma ^0} ( {{x_{\text{B}}}, {y_{\text{B}}}, t} ) A + {C_{\text{B}}}{\dot u^0} ( {{x_{\text{B}}}, {y_{\text{B}}}, t} ) A + {K_{\text{B}}}{u^0} ( {{x_{\text{B}}}, {y_{\text{B}}}, t} ) A \text{,} $$ (3) 式中:$ {F}_{\mathrm{B}} ( t ) $为边界节点处的等效节点力;${\sigma ^0} ( {{x_{\text{B}}}, {y_{\text{B}}}, t} ) $,${u^0} ( {{x_{\text{B}}}, {y_{\text{B}}}, t} ) $和${\dot u^0} ( {{x_{\text{B}}}, {y_{\text{B}}}, t} ) $分别为原自由场在边界处的应力、位移和速度,其中速度和应力可以根据边界处位移求得;KB和CB分别为黏弹性边界上的弹簧刚度系数和阻尼器的阻尼系数;A为节点控制面积。
在此基础上,刘晶波等(2018)提出新的地震动输入法,新方法可避免计算每一个边界节点处的自由场应力及由边界单元引起的附加荷载,也无需根据人工边界面的外法线确定等效节点力的作用方向,可简化等效节点力的计算过程。原有波动法在输入等效节点力后,有限元节点的动力方程为:
$$ {\boldsymbol{M}}\ddot {\boldsymbol{u}} + {\boldsymbol{C}}\dot {\boldsymbol{u}} + {\boldsymbol{Ku}} = {\boldsymbol{F}} \text{,} $$ (4) 式中,M,C和K分别为模型质量矩阵、阻尼矩阵和刚度矩阵;$ {\boldsymbol{u}} $,$ \dot {\boldsymbol{u}} $和$ \ddot {\boldsymbol{u}} $分别为模型节点位移、速度和加速度向量;$ {{\boldsymbol{F}}} $为输入的等效节点力向量。输入等效节点力后,模型的位移场与自由波场一致,根据自由波场运动方程可得:
$$ {\boldsymbol{F}} = {{\boldsymbol{M}}^0}{\ddot {\boldsymbol{u}}^0} + {{\boldsymbol{C}}^0}{\dot {\boldsymbol{u}}^0} + {{\boldsymbol{K}}^0}{{\boldsymbol{u}}^0} \text{,} $$ (5) 式中,上标0表示自由波场,若已知自由场,可根据式(5)计算等效节点力。原波动法需要对整个自由场模型进行计算,现仅需对子结构进行计算,即
$$ {{\boldsymbol{F}}_{\text{B}}} = {{\boldsymbol{M}}_{\text{BC}}}\ddot {\boldsymbol{u}}_{\text{C}}^0 + {{\boldsymbol{M}}_{\text{BB}}}\ddot {\boldsymbol{u}}_{\text{B}}^0 + {{\boldsymbol{C}}_{\text{BC}}}\dot {\boldsymbol{u}}_{\text{C}}^0 + {{\boldsymbol{C}}_{\text{BB}}}\dot {\boldsymbol{u}}_{\text{B}}^0 + {{\boldsymbol{K}}_{\text{BC}}}{\boldsymbol{u}}_{\text{C}}^0 + {{\boldsymbol{K}}_{\text{BB}}}{\boldsymbol{u}}_{\text{B}}^0 \text{,} $$ (6) 式中,下标B,C分别表示边界单元节点和相邻土体节点。式(6)表明,只要保证边界单元节点和相邻土体节点的运动与自由场一致,则人工边界节点上的外荷载即为所需的等效节点力。
等效地震荷载输入的具体实施步骤为:① 根据三维河谷地形模型的空间尺寸建立三维人工边界子结构模型,如图4所示,对子结构模型最外侧节点设置弹簧—阻尼器;② 利用一维计算程序算得自由场位移时程u0;③ 对子结构模型所有节点输入相应的u0,进行子结构动力反应分析,计算求得人工边界节点处的反力FB即为等效地震荷载;④ 用代码自动读取和写入大批量节点时程数据,施加到三维河谷地形模型中,实现地震动输入。
1.4 地震动输入方法的精度验证
以三维弹性均匀半空间模型为例,验证黏弹性人工边界子结构地震动输入方法的可靠性。首先通过引入人工边界截取长、宽、高分别为60 m,60 m和30 m的有限计算区域,其密度为2 000 kg/m3,剪切波速为200 m/s,泊松比为0.3。结合有限元计算精度要求,确定有限离散单元大小为2 m×2 m×2 m,以此有限离散单元对计算区域进行离散,形成如图5a所示的弹性均匀半空间有限元离散模型。针对离散后的有限元模型建立动力运动方程,并利用ABAQUS软件中的ABAQUS/Standard模块求解计算区域内节点的地震反应。对于人工边界上节点的地震反应则采用黏弹性人工边界子结构法计算得到,子结构模型如图5b所示。入射地震动选用宽0.3 s、持时1 s的单峰脉冲地震动,其位移幅值为1 m,位移时程及其傅里叶振幅谱如图6所示。
计算得到垂直入射脉冲地震动作用下,三维弹性均匀半空间有限元模型的位移反应,图7给出了地表测点和底边界测点的位移时程。由图7可知,地表位移峰值为2 m,底边界位移峰值为1 m。由弹性均匀半空间波动理论可知,自由表面位移幅值应为入射地震动的两倍。同时在底边界处的上行波和下行波的幅值均为1 m,表明人工边界具有足够的精度,未对位移反应产生影响。这两方面验证了人工边界子结构地震动输入方法的可靠性。
2. 有限元数值模拟结果分析
2.1 地形效应时域特性分析
本文采用有限元法结合黏弹性边界,通过时域动力有限元方法研究河谷场地地震动.数值模拟得到了各测点的位移反应,以此为基础讨论了各测点地震动反应峰值和质点运动轨迹。
2.1.1 峰值结果分析
由于河谷场地水平x向即地面运动主方向有更大的地震响应,此处仅针对水平x向的响应进行讨论。图8为河谷地形表面各测点处的水平x向位移时程曲线,图9为各测点水平x向的位移峰值较输入地震动的放大系数图。由图8和图9可知,由于地形的不对称,河谷两边地震响应存在差异;河谷两岸坡顶处位移峰值放大显著,向两岸逐渐衰减至输入地震动的两倍;随坡高的增加,位移峰值呈增大趋势;测点4和测点12距测点8的水平距离相同,但放大系数存在明显差异,结合图1可知,这是由左坡下坡角大于右坡下坡角所致,即坡度越大,位移峰值放大越显著。这表明河谷地形效应引起了显著的地震动强度的差动效应。
2.1.2 质点运动轨迹
由于分析模型实为二维问题,故在数值分析时仅考虑了输入地震动水平方向(x向)及入射方向(y向)的变化,并讨论了地形引起的地震动转换效应,图10给出了河谷表面一些测点的质点运动轨迹。由图可知,由于地形的复杂性,地震动在该区域的散射也较为复杂,各测点除有水平x向位移外,皆有竖直y向运动分量,表明各测点均存在地震动转换;两岸靠近边界的测点主要以水平往复运动为主,而由于两岸坡顶处存在着面的相交及转化,出现较强烈的地震动转换,其运动轨迹呈近似逆进椭圆;坡上各测点侧向运动及转向运动较大;对比测点4与测点8及测点8与测点12可以看出,前者地震动转换较后者更为明显,这是由左坡下坡角较大导致的。上述分析结果表明,河谷地形效应能产生明显的地震动转换,其特征为逆进椭圆面波。
2.2 地形效应频域特性分析
基于时域数值模拟结果,从频域角度进行了地形效应的相干性及相位特性的分析,即以测点1为参考点,计算了其余各测点的地震反应与测点1的相干系数及相位差。
2.2.1 相干性分析
对于两个计算点i和j,相干系数的计算公式(万珂羽,孙晓丹,2022)为:
$$ \left| {{\gamma _{ij}} ( \omega ) } \right| = \frac{{\left| { {{\overline S_{ij}} ( \omega ) } } \right|}}{{\sqrt { {{\overline S_{ii}} ( \omega ) {\overline S_{jj}} ( \omega ) } } }} \text{,} $$ (7) 式中,$ {{\overline S_{ii}} ( \omega ) }$,$ {{\overline S_{jj}} ( \omega ) }$,$ {{\overline S_{ij}} ( \omega ) }$分别为平滑后i,j点的自功率谱及两点间的互功率谱,本文采用汉明(Hamming)窗进行谱的平滑化,并据此计算得到了测点2至测点15相对于测点1的相干系数。相干系数是描述不同点间地震动相关程度的量,其值介于0至1之间,值越大表明两点间的相干性越强,0表示两点互不相干,1表示两点地震动过程完全一致。
图11展示了测点2至测点15与测点1之间地震动的相干系数随频率的变化关系。由图可知,两岸各测点间地震动的相干性较好,基本趋于1;坡上各测点地震动由于其复杂的散射效应,与测点1的相干性较差;随着坡高的降低,相干性逐渐降低;相干性最差的区域集中在测点7至测点10,即谷底及其周围小范围影响区域。由此可知,河谷地形效应将减小地震动的相干性。
2.2.2 相位差分析
图12为测点2至测点15与测点1之间地震动的相位差图。由图可知,两岸各测点间的地震动几乎不存在相位差;坡上各测点地震动与测点1之间的地震动存在显著的相位差,且相位差与场点位置相关,即各测点间皆存在不同的相位差,但相邻测点地震动相位差较相近。由此可以认为,河谷地形效应会导致地震动的相位差。
3. 讨论与结论
本文针对西部某桥梁工程三维河谷地形场地,采用与黏弹性人工边界相结合的时域隐式动力有限元方法,在垂直入射下分析了河谷地形对地震动的影响,得到以下主要结论:
1) 河谷地形对地震动强度有显著影响,且与河谷特征及场点位置相关,河谷底部地震动明显小于顶部和斜坡,河谷两岸坡顶处位移峰值放大最明显;随坡度的增大,位移峰值呈增长趋势。
2) 河谷地形能产生特征为近似逆进椭圆的地震动转换,且两岸坡顶处地震动转换显著;随坡度的增加,地震动转换更明显。
3) 河谷地形效应会减小地震动的相干性;河谷两岸地震动之间相干性较好,而与坡上地震动相干性较差;随边坡下降,地震动相干性逐渐降低,谷底地震动相干性最小。
4) 河谷地形效应会引发地震动的相位差,且与边坡上场点位置相关,但相邻场点相位差相近;河谷两岸地震动之间几乎不存在相位差,而边坡及谷底相位差较大。
5) 河谷地形会导致地震动明显的差动效应,即峰值差动、相位差,同时降低地震动的相干性。
本研究可为开展非一致激励下河谷场地的桥梁三维地震反应分析提供参考依据,后续可进一步进行土结相互作用研究。
-
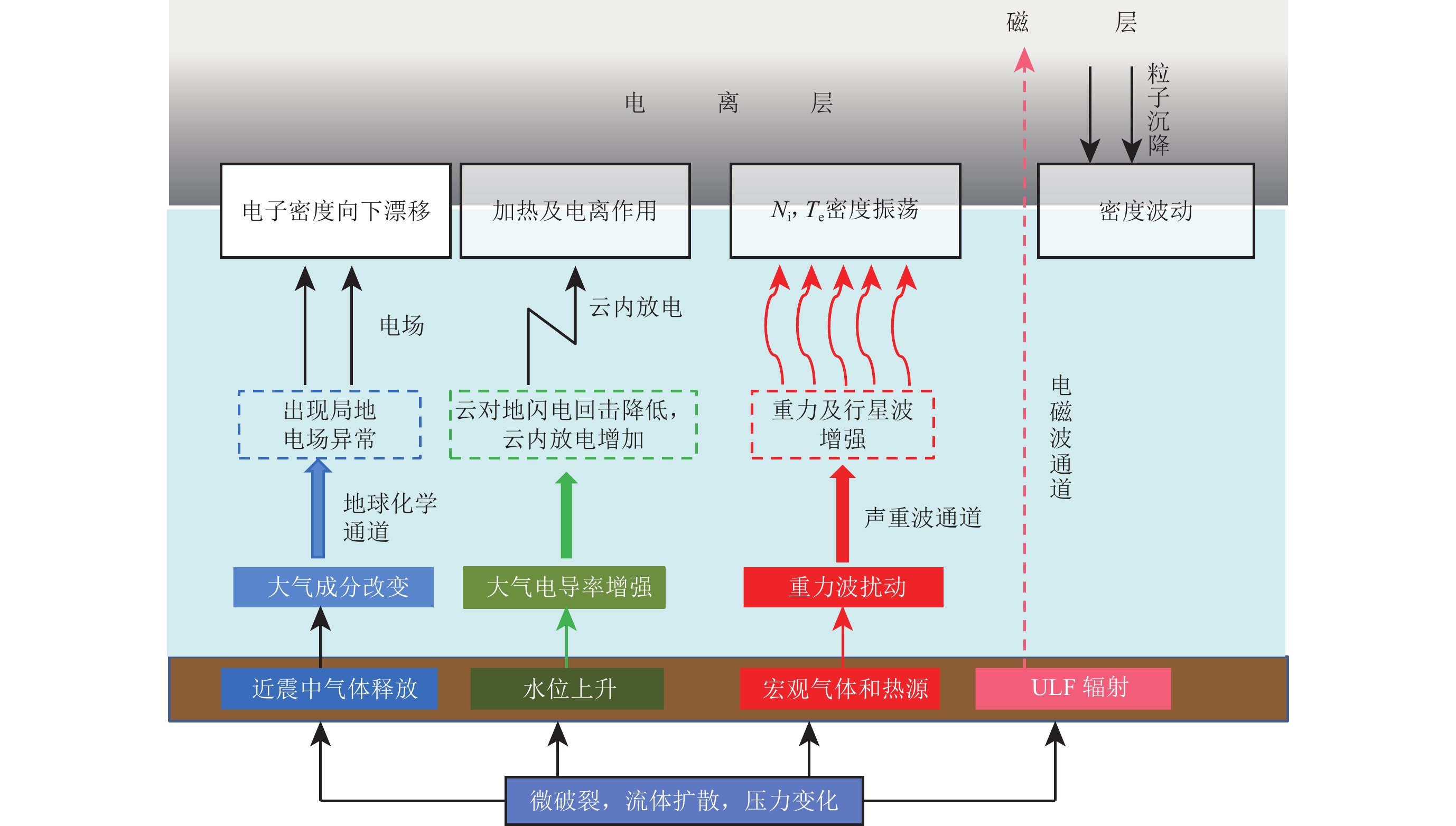
图 5 岩石层-大气层-电离层圈层耦合机理及耦合通道(引自Hayakawa,2004)
Figure 5. Lithosphere-atmosphere-ionosphere coupling mechanism and channels (from Hayakawa,2004)
图 1 1995年1月17日日本神户MS7.2地震前后晨昏时间位移异常(引自Molchanov et al,1998b)
tm为早晨日出时间,te为黄昏日落时间,图中阴影区为异常;Nph为对应低点的相位值,*为地震当日
Figure 1. The TTs anomalies around Kobe MS7.2 earthquake on 17 January 1995 (Molchanov et al,1998b)
x-axis indicates the local time of 0−24,tm is the morning time,te is the evening time,the shadow areas are the anomalies;Nph denote the phase corresponding to the lowest TTs anomalies,* denotes the earthquake occurrence time
图 2 2011年3月11日东日本大地震前后VLF信号夜侧平均幅值T和离差D的归一化标准差直方图以及M-t地震序列(Hayakawa et al,2018)
Figure 2. The histogram of nighttime average amplitude (T) and deviation (D) of VLF signals around Tohoku earthquake in Japan on 11 March 2011 and the M-t series plot of this earthquake (Hayakawa et al,2018)
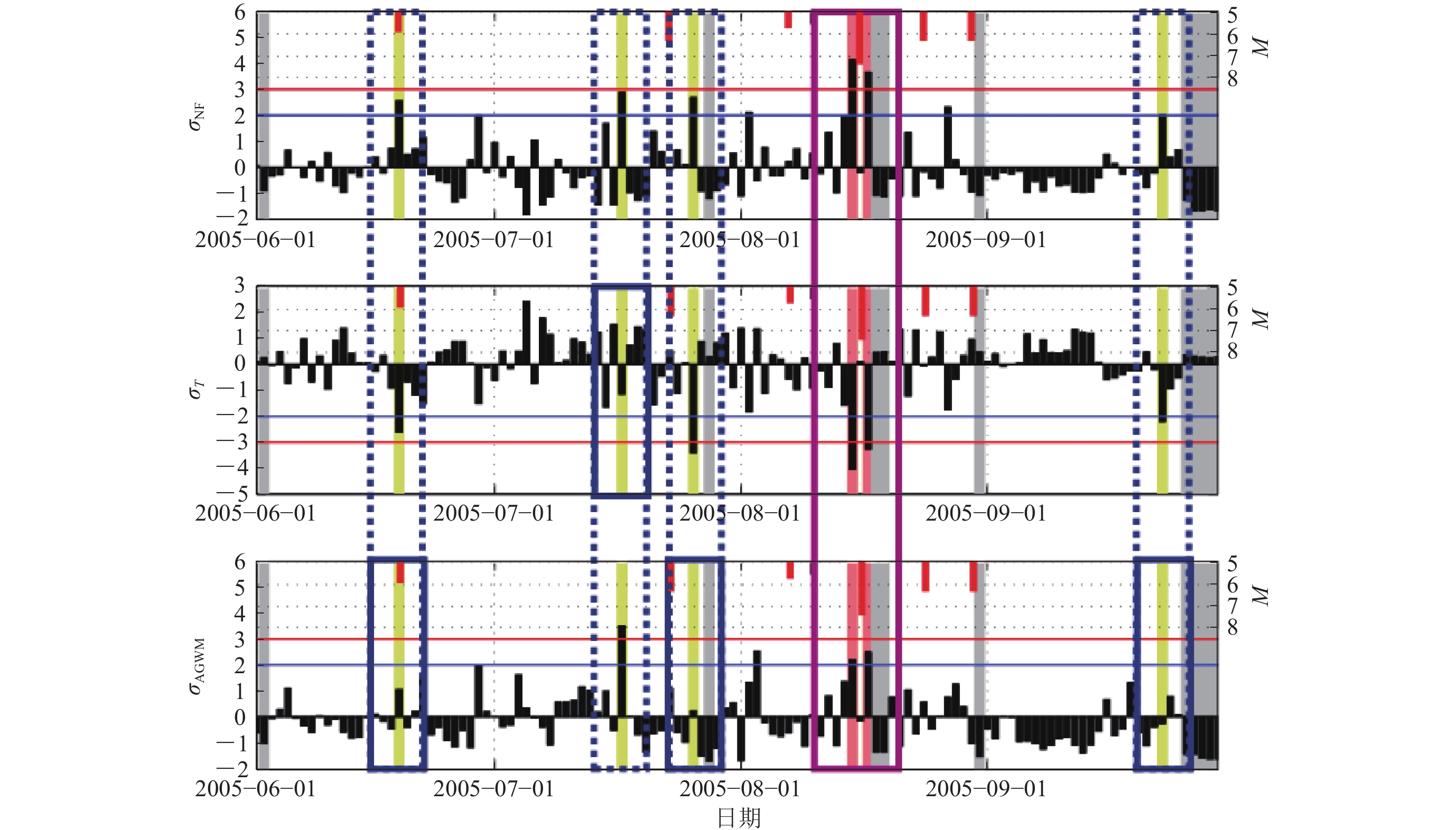
图 3 2005年6—9月VLF 观测链路上夜测波动NF,平均幅值T和AGWM的归一化标准差σ直方图及区域M5.0以上地震的M-t图(顶部红色垂线)(Muto et al,2009)
Figure 3. The normalized standard deviation histogram of three parameters ( NF,T,and AGWM) along the VLF observing link of JJY-KCK and the M-t plot of the M≥5.0 earthquakes (the red vertical line at the top of each panel) in the area during June to September in 2005 (Muto et al,2009)
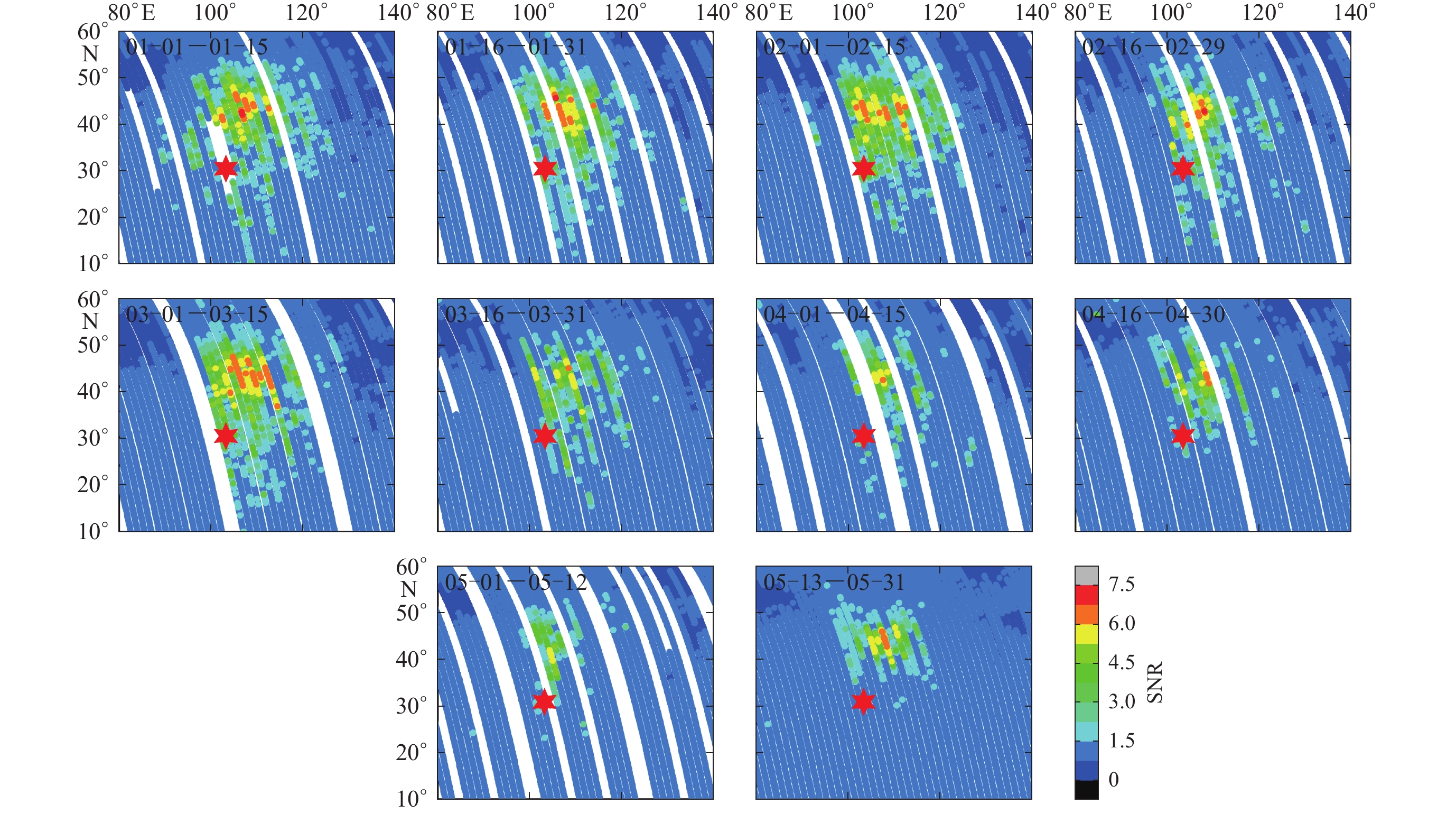
图 4 2008年5月12日汶川MS8.0地震前后低频人工源信号SNR时空演化图(1—5月,每半月一张图;引自Zhang et al,2019)
Figure 4. The spatio-temporal variations of SNR from LF transmitter signals around Wenchuan MS8.0 earthquake on 12 May 2008 (during January to May with half month for each panel,from Zhang et al,2019)
表 1 中国无线电频率划分表
Table 1 Regulations on the radio frequency allocation in China
带号 频 带 名 称 频 率 范 围 波 段 名 称 波 长 范 围 −1 至低频(TLF) 0.03—0.3 Hz 至长波或千兆米波 10 000—1 000 Mm 0 至低频(TLF) 0.3—3 Hz 至长波或百兆米波 1000—100 Mm 1 极低频(ELF) 3—30 Hz 极长波 100—10 Mm 2 超低频(SLF) 30—300 Hz 超长波 10—1 Mm 3 特低频(ULF) 300—3 000 Hz 特长波 1000—100 km 4 甚低频(VLF) 3—30 kHz 甚长波 100—10 km 5 低频(LF) 30—300 kHz 长波 10—1 km 6 中频(MF) 300—3 000 kHz 中波 1000—100 m 7 高频(HF) 3—30 MHz 短波 100—10 m 8 甚高频(VHF) 30—300 MHz 米波 10—1 m 9 特高频(UHF) 300—3000 MHz 分米波 10—1 dm 10 超高频(SHF) 3—30 GHz 厘米波 10—1 cm 11 极高频(EHF) 30—300 GHz 毫米波 10—1 mm 12 至高频(THF) 300—3 000 GHz 丝米波或亚毫米波 10—1 dmm -
何宇飞,杨冬梅,陈化然,钱家栋,朱荣,Parrot M. 2009. DEMETER卫星探测到可能与汶川地震有关的地面VLF发射站信号的信噪比变化[J]. 中国科学:D辑,39(4):403–412. He Y F,Yang D M,Chen H R,Qian J D,Zhu R,Parrot M. 2009. SNR changes of VLF radio signals detected onboard the DEMETER satellite and their possible relationship to the Wenchuan earthquake[J]. Science in China:Series D,52(6):754–763. doi: 10.1007/s11430-009-0064-5
廖力,赵庶凡,申旭辉,汪枫,泽仁志玛,黄建平,张学民,欧阳新艳,鲁恒新. 2019. ZH-1卫星观测的VLF人工源信号特征分析与全波模拟[J]. 地球物理学报,62(4):1210–1217. doi: 10.6038/cjg2019M0504 Liao L,Zhao S F,Shen X H,Wang F,Zeren Z M,Huang J P,Zhang X M,Ouyang X Y,Lu H X. 2019. Characteristic analysis and full wave simulation of electrical field for China Seismo-Electromagnetic Satellite observations radiated from VLF transmitter[J]. Chinese Journal of Geophysics,62(4):1210–1217 (in Chinese).
张学民,赵国泽,陈小斌,马为. 2007. 国外地震电磁现象观测[J]. 地球物理学进展,22(3):687–694. doi: 10.3969/j.issn.1004-2903.2007.03.005 Zhang X M,Zhao G Z,Chen X B,Ma W. 2007. Seismo-electromagnetic observation abroad[J]. Progress in Geophysics,22(3):687–694 (in Chinese).
张学民,申旭辉,赵庶凡,刘静,欧阳新艳,娄文宇,泽仁志玛,何建辉,钱庚. 2016. 地震电离层探测技术及其应用研究进展[J]. 地震学报,38(3):356–375. doi: 10.11939/jass.2016.03.004 Zhang X M,Shen X H,Zhao S F,Liu J,Ouyang X Y,Lou W Y,Zeren Z M,He J H,Qian G. 2016. The seismo-ionospheric monitoring technologies and their application research development[J]. Acta Seismologica Sinica,38(3):356–375 (in Chinese).
张学民,钱家栋,申旭辉,刘静,王亚璐,黄建平,赵庶凡,欧阳新艳. 2020. 电磁卫星地震应用进展及未来发展思考[J]. 地震,40(2):18–37. doi: 10.12196/j.issn.1000-3274.2020.02.002 Zhang X M,Qian J D,Shen X H,Liu J,Wang Y L,Huang J P,Zhao S F,Ouyang X Y. 2020. The seismic application progress in electromagnetic satellite and future development[J]. Earthquake,40(2):18–37 (in Chinese).
中华人民共和国工业和信息化部. 2019. 中华人民共和国无线电频率划分规定[EB/OL]. [2021-06-09]. http://www.srrc.org.cn/article23480.aspx. Ministry of Industry and Information Technology of the People’s Republic of China. 2019. People’s Republic of China regulations on the radio frequency allocation[EB/OL]. [2021-06-09]. http://www.srrc.org.cn/article23480.aspx (in Chinese).
Baba K,Hayakawa M. 1995. The effect of localized ionospheric perturbations on subionospheric VLF propagation on the basis of finite element method[J]. Radio Sci,30(5):1511–1517. doi: 10.1029/95RS01561
Bell T F,Graf K,Inan U S,Piddyachiy D,Parrot M. 2011. DEMETER observations of ionospheric heating by powerful VLF transmitters[J]. Geophys Res Lett,38(11):L11103. doi: 10.1029/2011GL047503
Biagi P F, Hayakawa M. 2002. Possible premonitory behaviour of LF radiowaves on the occasion of the Slovenia earthquakes (M=5.2−6.0−5.1) occurred on March–May 1998[G]//Seismo-Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling. Tokyo: TERRAPUB: 249−253.
Biagi P F,Piccolo R,Castellana L,Ermini A,Martellucci S,Bellecci C,Capozzi V,Perna G,Molchanov O,Hayakawa M. 2004. Variations in a LF radio signal on the occasion of the recent seismic and volcanic activity in southern Italy[J]. Phys Chem Earth A/B/C,29(4/5/6/7/8//9):551–557.
Biagi P F,Maggipinto T,Righetti F,Loiacono D,Schiavulli L,Ligonzo T,Ermini A,Moldovan I A,Moldovan A S,Buyuksarac A,Silva H G,Bezzeghoud M,Contadakis M E. 2011. The European VLF/LF radio network to search for earthquake precursors:Setting up and natural/man-made disturbances[J]. Nat Hazards Earth Syst Sci,11(2):333–341. doi: 10.5194/nhess-11-333-2011
Biagi P F,Righetti F,Maggipinto T,Schiavulli L,Ligonzo T,Ermini A,Moldovan I A,Moldovan A S,Silva H G,Bezzeghoud M,Contadakis M E,Arabelos D N,Xenos T D,Buyuksarac A. 2012. Anomalies observed in VLF and LF radio signals on the occasion of the western Turkey earthquake (MW=5.7) on May 19,2011[J]. Int J Geosci,3(4A):856–865.
Chakraborty S,Sasmal S,Chakrabarti S K,Bhattacharya A. 2018. Observational signatures of unusual outgoing longwave radiation (OLR) and atmospheric gravity waves (AGW) as precursory effects of May 2015 Nepal earthquakes[J]. J Geodyn,113:43–51. doi: 10.1016/j.jog.2017.11.009
Chen C H,Lin L C,Yeh T K,Wen S,Yu H,Chen Y,Gao Y,Han P,Sun Y Y,Liu J Y, Lin C H,Tang C C,Lin C M,Hsieh H H, Lu P J. 2020a. Determination of epicenters before earthquakes utilizing far seismic and GNSS data:Insights from ground vibrations[J]. Remote Sens,12:3252. doi: 10.3390/rs12193252
Chen C H,Sun Y Y,Wen S,Han P,Lin L C,Yu H Z,Zhang X M,Gao Y X,Tang C C,Lin C H,Liu J Y. 2020b. Spatiotemporal changes of seismicity rate during earthquakes[J]. Nat Hazards Earth Syst Sci,20(12):3333–3341. doi: 10.5194/nhess-20-3333-2020
Chen Y P,Yang G B,Ni B B,Zhao Z Y,Gu X D,Zhou C,Wang F. 2016. Development of ground-based ELF/VLF receiver system in Wuhan and its first results[J]. Adv Space Res,57(9):1871–1880. doi: 10.1016/j.asr.2016.01.023
Cohen M B,Inan U S,Paschal E W. 2010. Sensitive broadband ELF/VLF radio reception with the AWESOME instrument[J]. IEEE Trans Geosci Remote Sens,48(1):3–17. doi: 10.1109/TGRS.2009.2028334
Cohen M B,Marshall R A. 2012. ELF/VLF recordings during the 11 March 2011 Japanese Tohoku earthquake[J]. Geophys Res Lett,39(11):L11804. doi: 10.1029/2012GL052123
Freund F. 2000. Time-resolved study of charge generation and propagation in igneous rocks[J]. J Geophys Res:Solid Earth,105(B5):11001–11019. doi: 10.1029/1999JB900423
Freund F. 2002. Charge generation and propagation in igneous rocks[J]. J Geodyn,33(4/5):543–570. doi: 10.1016/S0264-3707(02)00015-7
Freund F,Sornette D. 2007. Electro-magnetic earthquake bursts and critical rupture of peroxy bond networks in rocks[J]. Tectonophysics,431(1//2/3/4):33–47. doi: 10.1016/j.tecto.2006.05.032
Freund F T,Kulahci I G,Cyr G,Lin J L,Winnick M,Tregloan-Reed J,Freund M M. 2009. Air ionization at rock surfaces and pre-earthquake signals[J]. J Atmos Sol Terr Phys,71(17/18):1824–1834. doi: 10.1016/j.jastp.2009.07.013
Freund F. 2010. Toward a unified solid state theory for pre-earthquake signals[J]. Acta Geophys,58(5):719–766. doi: 10.2478/s11600-009-0066-x
Hao Y Q,Xiao Z,Zhang D H. 2012. Multi-instrument observation on co-seismic ionospheric effects after great Tohoku earthquake[J]. J Geophys Res:Space Phys,117(A2):A02305. doi: 10.1029/2011JA017036
Hayakawa M,Molchanov O A,Ondoh T,Kawai E. 1996a. The precursory signature effect of the Kobe earthquake on VLF subionospheric signals[J]. J Commun Res Lab,43(2):169–180.
Hayakawa M,Molchanov O A,Ondoh T,Kawai E. 1996b. Anomalies in the sub-ionospheric VLF signals for the 1995 Hyogo-Ken Nanbu earthquake[J]. J Phys Earth,44(4):413–418. doi: 10.4294/jpe1952.44.413
Hayakawa M. 1999. Atmospheric and Ionospheric Electromagnetic Phenomena Associated With Earthquakes[M]. Tokyo: TERRAPUB: 996.
Hayakawa M, Molchanov O A. 2002. Seismo Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling[M]. Tokyo: TERRAPUB: 477.
Hayakawa M. 2004. Electromagnetic phenomena associated with earthquakes:A frontier in terrestrial electromagnetic noise environment[J]. Recent Res Devel Geophys,6:81–112.
Hayakawa M,Horie T,Muto F,Kasahara Y,Ohta K,Liu J Y,Hobara Y. 2010a. Subionospheric VLF/LF probing of ionospheric perturbations associated with earthquakes:A possibility of earthquake prediction[J]. SICE J Control,Meas,Syst Integrat,3(1):10–14.
Hayakawa M,Kasahara Y,Nakamura T,Muto F,Horie T,Maekawa S,Hobara Y,Rozhnoi A A,Solovieva M,Molchanov O A. 2010b. A statistical study on the correlation between lower ionospheric perturbations as seen by subionospheric VLF/LF propagation and earthquakes[J]. J Geophys Res:Space Phys,115(A9):A09305. doi: 10.1029/2009JA015143
Hayakawa M,Raulin J P,Kasahara Y,Bertoni F C P,Hobara Y,Guevara-Day W. 2011. Ionospheric perturbations in possible association with the 2010 Haiti earthquake,as based on medium-distance subionospheric VLF propagation data[J]. Nat Hazards Earth Syst Sci,11(2):513–518. doi: 10.5194/nhess-11-513-2011
Hayakawa M,Hobara Y,Yasuda Y,Yamaguchi H,Ohta K,Izutsu J,Nakamura T. 2012. Possible precursor to the March 11,2011,Japan earthquake:Ionospheric perturbations as seen by subionospheric very low frequency/low frequency propagation[J]. Ann Geophys,55(1):95–99.
Hayakawa M,Hobara Y,Rozhnoi A,Solovieva M,Ohta K,Izutsu J,Nakamura T,Kasahara Y. 2013a. The ionospheric precursor to the 2011 March 11 earthquake based upon observations obtained from the Japan-Pacific subionospheric VLF/LF network[J]. Terr Atmos Ocean Sci,24(3):393–408. doi: 10.3319/TAO.2012.12.14.01(AA)
Hayakawa M,Rozhnoi A,Solovieva M,Hobara Y,Ohta K,Schekotov A,Fedorov E. 2013b. The lower ionospheric perturbation as a precursor to the 11 March 2011 Japan earthquake[J]. Geomat Natl Hazards Risk,4(3):275–287. doi: 10.1080/19475705.2012.751938
Hayakawa M, Asano T, Rozhnoi A, Solovieva M. 2018. Very-low- to low-frequency sounding of ionospheric perturbations and possible association with earthquakes[G]//Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies. Washington: American Geophysical Union: 1−361.
Horie T,Maekawa S,Yamauchi T,Hayakawa M. 2007. A possible effect of ionospheric perturbations associated with the Sumatra earthquake,as revealed from subionospheric very‐low‐frequency (VLF) propagation (NWC-Japan)[J]. Int J Remote Sens,28(13/14):3133–3139.
Jin S G,Zhu W,Afraimovich E. 2010. Co-seismic ionospheric and deformation signals on the 2008 magnitude 8.0 Wenchuan earthquake from GPS observations[J]. Int J Remote Sens,31(13):3535–3543. doi: 10.1080/01431161003727739
Kasahara Y,Muto F,Horie T,Yoshida M,Hayakawa M,Ohta K,Rozhnoi A,Solovieva M,Molchanov O A. 2008. On the statistical correlation between the ionospheric perturbations as detected by subionospheric VLF/LF propagation anomalies and earthquakes[J]. Nat Hazards Earth Syst Sci,8(4):653–656. doi: 10.5194/nhess-8-653-2008
Kuo C L,Huba J D,Joyce G,Lee L C. 2011. Ionosphere plasma bubbles and density variations induced by pre-earthquake rock currents and associated surface charges[J]. J Geophys Res:Space Phys,116(A10):A10317. doi: 10.1029/2011JA016628
Kuo C L,Lee L C,Huba J D. 2014. An improved coupling model for the lithosphere-atmosphere-ionosphere system[J]. J Geophys Res:Space Phys,119(4):3189–3205. doi: 10.1002/2013JA019392
Li X Q,Ma Y Q,Wang P,Wang H Y,Lu H,Zhang X M,Huang J P,Shi F,Yu X X,Xu Y B,Meng X C,Wang H,Zhao X Y,Parrot M. 2012. Study of the North West Cape electron belts observed by DEMETER satellite[J]. J Geophys Res:Space Phys,117(A4):A04201. doi: 10.1029/2011JA017121
Loudet L. 2013. SID monitoring station[EB/OL]. [2021-06-18]. https://sidstation.loudet.org/stations-list-en.xhtml.
Maekawa S,Horie T,Yamauchi T,Sawaya T,Ishikawa M,Hayakawa M,Sasaki H. 2006. A statistical study on the effect of earthquakes on the ionosphere,based on the subionospheric LF propagation data in Japan[J]. Ann Geophys,24(8):2219–2225. doi: 10.5194/angeo-24-2219-2006
Maggipinto T,Biagi P F,Colella R,Schiavulli L,Ligonzo T,Ermini A,Martinelli G,Moldovan I,Silva H,Contadakis M,Skeberis C,Zaharis Z,Scordilis E,Katzis K,Buyuksarac A,D’Amico S. 2015. The LF radio anomaly observed before the MW=6.5 earthquake in Crete on October 12,2013[J]. Phys Chem Earth A/B/C,85/86:98–105.
Maurya A K,Singh R,Veenadhari B,Kumar S,Singh A K. 2013. Sub-ionospheric VLF perturbations associated with the 12 May 2008 M7.9 Sichuan earthquake[J]. Nat Hazards Earth Syst Sci,13:2331–2336. doi: 10.5194/nhess-13-1-2013
Maurya A K,Venkatesham K,Tiwari P,Vijaykumar K,Singh R,Singh A K,Ramesh D S. 2016. The 25 April 2015 Nepal earthquake:Investigation of precursor in VLF subionospheric signal[J]. J Geophys Res:Space Phys,121(10):10403–10416. doi: 10.1002/2016JA022721
Molchanov O A,Hayakawa M. 1998. Subionospheric VLF signal perturbations possibly related to earthquakes[J]. J Geophys Res:Space Phys,103(A8):17489–17504. doi: 10.1029/98JA00999
Molchanov O A,Hayakawa M,Oudoh T,Kawai E. 1998. Precursory effects in the subionospheric VLF signals for the Kobe earthquake[J]. Phys Earth Planet Inter,105(3/4):239–248.
Molchanov O,Fedorov E,Schekotov A,Gordeev E,Chebrov V,Surkov V,Rozhnoi A,Andreevsky S,Iudin D,Yunga S,Lutikov A,Hayakawa M,Biagi P F. 2004. Lithosphere-atmosphere-ionosphere coupling as governing mechanism for preseismic short-term events in atmosphere and ionosphere[J]. Nat Hazards Earth Syst Sci,4(5/6):757–767. doi: 10.5194/nhess-4-757-2004
Molchanov O,Rozhnoi A,Solovieva M,Akentieva O,Berthelier J J,Parrot M,Lefeuvre F,Biagi P F,Castellana L,Hayakawa M. 2006. Global diagnostics of the ionospheric perturbations related to the seismic activity using the VLF radio signals collected on the DEMETER satellite[J]. Nat Hazards Earth Syst Sci,6(5):745–753. doi: 10.5194/nhess-6-745-2006
Muto F,Yoshida M,Horie T,Hayakawa M,Parrot M,Molchanov O A. 2008. Detection of ionospheric perturbations associated with Japanese earthquakes on the basis of reception of LF transmitter signals on the satellite DEMETER[J]. Nat Hazards Earth Syst Sci,8:135–141. doi: 10.5194/nhess-8-135-2008
Muto F,Kasahara Y,Hobara Y,Hayakawa M,Rozhnoi A,Solovieva M,Molchanov O A. 2009. Further study on the role of atmospheric gravity waves on the seismo-ionospheric perturbations as detected by subionospheric VLF/LF propagation[J]. Nat Hazards Earth Syst Sci,9(4):1111–1118. doi: 10.5194/nhess-9-1111-2009
Parrot M. 2018. DEMETER observations of manmade waves that propagate in the ionosphere[J]. C R Phys,19(1/2):26–35.
Phanikumar D V,Maurya A K,Kumar K N,Venkatesham K,Singh R,Sharma S,Naja M. 2018. Anomalous variations of VLF sub-ionospheric signal and Mesospheric Ozone prior to 2015 Gorkha Nepal earthquake[J]. Sci Rep,8(1):9381. doi: 10.1038/s41598-018-27659-9
Rozhnoi A,Solovieva M S,Molchanov O A,Hayakawa M. 2004. Middle latitude LF (40 kHz) phase variations associated with earthquakes for quiet and disturbed geomagnetic conditions[J]. Phys Chem Earth A/B/C,29(4/9):589–598.
Rozhnoi A,Solovieva M,Molchanov O,Akentieva O,Berthelier J J,Parrot M,Biagi P F,Hayakawa M. 2008. Statistical correlation of spectral broadening in VLF transmitter signal and low-frequency ionospheric turbulence from observation on DEMETER satellite[J]. Nat Hazards Earth Syst Sci,8(5):1105–1111. doi: 10.5194/nhess-8-1105-2008
Rozhnoi A,Solovieva M,Molchanov O,Schwingenschuh K,Boudjada M,Biagi P F,Maggipinto T,Castellana L,Ermini A,Hayakawa M. 2009. Anomalies in VLF radio signals prior the Abruzzo earthquake (M=6.3) on 6 April 2009[J]. Nat Hazards Earth Syst Sci,9(5):1727–1732. doi: 10.5194/nhess-9-1727-2009
Rozhnoi A,Shalimov S,Solovieva M,Levin B,Hayakawa M,Walker S. 2012. Tsunami-induced phase and amplitude perturbations of subionospheric VLF signals[J]. J Geophys Res:Space Phys,117(A9):A09313. doi: 10.1029/2012JA017761
Rozhnoi A,Shalimov S,Solovieva M,Levin B,Shevchenko G,Hayakawa M,Hobara Y,Walker S N,Fedun V. 2014. Detection of tsunami-driven phase and amplitude perturbations of subionospheric VLF signals following the 2010 Chile earthquake[J]. J Geophys Res:Space Phys,119(6):5012–5019. doi: 10.1002/2014JA019766
Rozhnoi A,Solovieva M,Parrot M,Hayakawa M,Biagi P F,Schwingenschuh K,Fedun V. 2015. VLF/LF signal studies of the ionospheric response to strong seismic activity in the Far Eastern region combining the DEMETER and ground-based observations[J]. J Phys Chem Earth A/B/C,85/86:141–149. doi: 10.1016/j.pce.2015.02.005
Shen X H,Zeren Z M,Zhao S F,Qian G,Ye Q,Ruzhin Y R. 2017. VLF radio wave anomalies associated with the 2010 MS7.1 Yushu earthquake[J]. Adv Space Res,59(10):2636–2644. doi: 10.1016/j.asr.2017.02.040
Shvets A V,Hayakawa M,Molchanov O A,Ando Y. 2004. A study of ionospheric response to regional seismic activity by VLF radio sounding[J]. Phys Chem Earth A/B/C,29(4/5/6/7/8/9):627–637.
Shvets A V,Nickolaenko A P,Koloskov A V,Yampolsky Yu M,Budanov O V,Shvets A A. 2019. Low-frequency (ELF–VLF) radio atmospherics study at the Ukrainian Antarctic Akademik Vernadsky station[J]. Ukrainian Antarct J,1(18):116–127.
Singh R,Veenadhari B,Cohen M B,Pant P,Singh A K,Maurya A K,Vohat P,Inan U S. 2010. Initial results from AWESOME VLF receivers:Set up in low latitude Indian regions under IHY2007/UNBSSI program[J]. Curr Sci,98(3):398–405.
Slominska E,Blecki J,Parrot M,Slominski J. 2009. Satellite study of VLF ground-based transmitter signals during seismic activity in Honshu Island[J]. Phys Chem Earth A/B/C,34(6/7):464–473. doi: 10.1016/j.pce.2008.06.016
Solovieva M S,Rozhnoi A A,Molchanov O A. 2009. Variations in the parameters of VLF signals on the DEMETER satellite during the periods of seismic activity[J]. Geomag Aeron,49(4):532–541. doi: 10.1134/S0016793209040161
Sorokin V M,Pokhotelov O A. 2014. Model for the VLF/LF radio signal anomalies formation associated with earthquakes[J]. Adv Space Res,54(12):2532–2539. doi: 10.1016/j.asr.2013.11.048
UK Radio Astronomy Association. 2021. VLF receiver[EB/OL]. [2021-06-18]. https://www.ukraa.com/store/categories/vlf-range/vlf-receiver.
Wang Y L,Zhang X M,Shen X H. 2018. A study on the energetic electron precipitation observed by CSES[J]. Earth Planet Phys,2(6):538–547.
Yang S S,Asano T,Hayakawa M. 2019. Abnormal gravity wave activity in the stratosphere prior to the 2016 Kumamoto earthquakes[J]. J Geophys Res:Space Phys,124(2):1410–1425. doi: 10.1029/2018JA026002
Zhang X M,Shen X H,Zhao S F,Yao Lu,Ouyang X Y,Qian J D. 2014. The characteristics of quasistatic electric field perturbations observed by DEMETER satellite before large earthquakes[J]. J Asian Earth Sci,79:42–52.
Zhang X M,Zhao S F,Song R,Zhai D L. 2019. The propagation features of LF radio waves at topside ionosphere and their variations possibly related to Wenchuan earthquake in 2008[J]. Adv Space Res,63(11):3536–3544. doi: 10.1016/j.asr.2019.02.008
Zhang X M,Wang Y L,Boudjada M Y,Liu J,Magnes W,Zhou Y L,Du X H. 2020. Multi-experiment observations of ionospheric disturbances as precursory effects of the Indonesian MS6.9 earthquake on August 05,2018[J]. Remote Sens,12(24):4050. doi: 10.3390/rs12244050
Zhao S F,Shen X H,Zeren Z M,Zhou C. 2020. The very low-frequency transmitter radio wave anomalies related to the 2010 MS7.1 Yushu earthquake observed by the DEMETER satellite and the possible mechanism[J]. Ann Geophys,38(5):969–981. doi: 10.5194/angeo-38-969-2020
Zhou C,Liu Y,Zhao S F,Liu J,Zhang X M,Huang H P,Shen X H,Ni B B,Zhao Z Y. 2017. An electric field penetration model for seismo-ionospheric research[J]. Adv Space Res,60(10):2217–2232. doi: 10.1016/j.asr.2017.08.007
-
期刊类型引用(1)
1. 郭明瑞,张宇,张兴国,王锡娇,张慧,曾涛,杨世杰,卢启明,庞雪华. 琼中地电场观测干扰排查实验分析. 地震地磁观测与研究. 2024(05): 98-106 .  百度学术
百度学术
其他类型引用(0)





 下载:
下载: