Geodynamical simulation of the effects of ridge subduction on the scale of the seismogenic zone south of Chile Triple Junction
-
摘要: 智利三联点以北地震较多，智利三联点以南地震很少且热异常显著。为探究洋脊俯冲对由温度定义的孕震区的影响，以智利三联点区域的地质背景为基础建立二维有限元数值模型，对洋脊俯冲过程进行数值模拟，并将俯冲角度和汇聚速率等因素对孕震区的影响进行了对比。结果表明，洋脊俯冲过程中孕震区宽度减小，导致发生在智利三联点以南的地震远少于智利三联点以北。剖面附近的观测数据与数值模拟结果的对比表明，数值模拟可以大致反映智利三联点区域板块间的孕震区宽度和地表热流特征。当俯冲汇聚量相同时，板块间的汇聚速率越大，洋脊俯冲过程中孕震区则越宽且其下边界越深，海沟附近的地表热流越高。与汇聚速率相比，俯冲角度等因素对地表热流的影响较小。俯冲角度越大，洋脊俯冲过程中孕震区越窄。当数值模型包含剪切生热时，洋脊俯冲过程中孕震区宽度大约可减小至15 km，且孕震区很浅。这可导致智利三联点以南部分区域难以发生地震，出现观测不到和达-贝尼奥夫带的现象。Abstract: Earthquakes are much more frequent to the north of Chile Triple Junction than to the south, where the thermal anomaly is also more significant. To study the effects of ridge subduction on the thermally defined seismogenic zone, two-dimensional finite element models were established based on the geology of Chile Triple Junction, the process of ridge subduction was simulated, and the effects of the initial slab dip and the convergence rate on the seismogenic zone were compared. The results show that the width of the seismogenic zone decreases during the ridge subduction, inducing earthquakes to occur much less to the south than to the north of Chile Triple Junction. By comparing the observed data in the vicinity of the profiles with the numerical simulation results, we find that the numerical simulation can roughly reflect the width of the interplate seismogenic zone and the surface heat flow in the area of Chile Triple Junction. At the same convergence distance, a larger convergence rate comes with a wider seismogenic zone and the deeper the downdip limit of the seismogenic zone, the higher the surface heat flow in the vicinity of the trench. Compared with the convergence rate, factors such as slab dip have little effect on the surface heat flow. In the process of ridge subduction, larger the slab dips leads to narrower seismogenic zones. When the effect of shear heating is included in the simulation, the width of the seismogenic zone in the process of ridge subduction can shrink to about 15 km and the depth of the seismogenic zone is small. Such a narrow and shallow seismogenic zone makes it hard for earthquakes to occur and for the Wadati-Benioff plane to be observed in some areas south of Chile Triple Junction.
-
Keywords:
- Chile Triple Junction /
- ridge subduction /
- seismogenic zone /
- numerical simulation
-
引言
高精度重力梯度测量作为一种新兴的地球物理探测技术，不仅在海洋重力辅助导航、 海底潜艇探测和海底资源勘探等领域具有重要意义(徐遵义等，2007； DiFrancesco et al，2009； Araya et al，2011)，而且在陆地资源勘探、 大型水库监测和水底坑洞探测等领域也是一种有效的地球物理探测技术(王谦身，2003; Woolrych et al，2015)． 此外，航空和卫星重力梯度测量在地球重力场等基础科学研究领域也具有重要的作用(宁津生等，1996，2002)．
自1971年美国空军首次提出精度为1 E的移动级重力梯度仪以来，高精度重力梯度仪的研究得到了迅速发展，其主要设计原理为差分加速度计和扭矩测量． 基于差分加速度计的航空重力梯度仪，由于其自身的高稳定性和高精度得到了迅速发展和应用(李红军等，2002； 刘凤鸣等，2009)，但大部分还处于实验样机阶段，目前唯一定型的商用重力梯度仪是美国贝尔实验室研制的旋转加速度计重力梯度仪(DiFrancesco et al，2009)． 基于扭矩测量的重力梯度仪，由于体积和稳定性问题，其发展受到了限制． 彭益武等(2006)设计的基于扭矩测量的二维簧片重力梯度仪在体积和稳定性等方面取得了突破． 另外，超导重力梯度仪由于其测量精度、 体积和整体质量等方面的优势，越来越多地被应用于航空重力测量中(吴琼等，2013)，具有非常好的发展前景(Moody et al，2002)．
上述各类梯度仪的设计原理均属于相对测量，需要对参考坐标及变化的物理量进行标定，不适用于发射到宇宙外星球进行长期的内部质量分布探测研究，因此，在美国宇航局20世纪末的火星探测计划中，Micro-G公司开展了基于激光干涉原理的绝对重力梯度仪的研制，其测量精度的设计指标为1 E，其目的是探测火星的深部结构(Brown et al，1999; Robertson，2001)．
受此启发，激光绝对重力梯度仪作为研究地球深部质量迁移的一种新型有效工具，更能满足地震的监测需求． 目前，我国差分加速度计的最高精度为10-6 m/s2，这与梯度仪要求的测量精度还有很大差距； 而现有的绝对重力测量技术的测量精度可达10-8 m/s2，完全能够满足重力梯度仪的精度要求(胡华等，2012； 滕云田等，2013)，故基于创新设计及软件开发，利用激光干涉法完成地表重力垂直梯度测量的方案是完全可行的． 虽然目前该仪器的体积较大，但从固定台站观测的角度看，该缺点可以忽略； 而且随着激光干涉重力梯度仪研究的进一步开展，将来可以进行小型化设计，使之满足移动重力垂直梯度仪的测量需求．
本文拟基于激光干涉法对新型地表重力垂直梯度测量系统进行研究并初步构建原理样机. 该测量系统采用激光干涉原理，通过测定两个落体同步自由下落时相对于刚性连接的两个参考点的位置信息确定各自的重力加速度，然后通过差分计算得到测点的重力垂直梯度． 由于两个参考点为刚性连接，其感受到地面的振动信息完全相同，且两个落体利用同一套伺服控制系统，由振动引入的测量误差将在差分时消除，这样即可得到某测点的高精度重力垂直梯度值． 与其它重力梯度仪相比，激光干涉重力梯度仪具有以下优点： ① 有较大的测量范围，无需标定，无漂移； ② 地面振动属于共模误差，无需设计特殊的隔振系统，对动态测量非常有利； ③ 地面倾斜属于共模误差； ④ 对地球浅层异常质量体敏感．
1. 设计原理
1.1 基本原理
基于激光干涉法重力垂直梯度测量的基本原理是，当两个落体在一个真空舱中同步自由下落时，运动过程中所受到的干扰因素可以等效为一个合力，并且该合力对每个落体的作用均相同，唯一不同的是所受重力场重力垂直梯度的影响． 因此，通过解算垂直向间隔为h的两个落体(较高位置的为上落体P1，较低位置的为下落体P2)在真空中作自由下落运动时测量得到的干涉条纹，分析重建各自的自由下落轨迹(吴琼等，2012)，并获取上落体P1在其有效测量高度href_U处的第一绝对重力加速度值gU和下落体P2在其有效测量高度href_D处的第二绝对重力加速度值gD，再根据下式得到单次下落的重力垂直梯度γ，即
(1) 图 1给出了重力梯度测量算法原理，主要是为了确定式(1)中的两个未知量href_U和href_D． 落体P1的初始位置为A00，其对应的初始速度和位移均为0，但在实际工作中一般将初始速度和位移无限接近于0的A0点作为其初始位置，在计算中近似认为A00与A0重合，因此hinst_U对应的是P1的初始位置． 在heff_U位置处，由于上落体P1在自由下落过程中所受到的重力梯度影响的综合效应为0，则测量得到的重力加速度值所对应的高度为
(2) 对于下落体P2，同样有
(3) ![]()
图 1 重力梯度测量算法原理Figure 1. Principle for the algorithm of the gravity vertical gradient measurement在计算重力垂直梯度时，首先计算heff_U和heff_D，然后将式(2)和(3)代入式(1)求得最终测点的垂直向重力梯度值． 对于heff_U和heff_D，二者采用的推导过程相同，这里仅以heff_U为例进行说明：
1)设定初始条件． 考虑到重力垂直梯度的测量精度要求，在heff_U的计算过程中，其计算精度须精确到mm； 对于上落体P1，从初始位置A00到位置A0的下落运动过程为非自由下落运动，距离一般小于5 μm，时间小于30 ms． 这段非自由下落运动过程对heff_U值的影响在误差允许范围内，因此在计算中可被忽略． 也就是说，假设上落体在t00时刻从初始位置A00开始进入自由下落运动，则t0=0，v0=0，x0=0； 初始位置A00的绝对重力加速度g0为已知设定值． 此外，(t1，x1)和(tn，xn)已根据所获取的干涉信号解算得到．
2) 落体的自由下落运动方程为
(4) 根据假设的初始条件，解上述方程，可得
(5) 由于gU是t1—tn时段内重力场平均作用于上落体P1的结果，则其表达式为
(6) 将式(5)代入式(6)，得
(7) 又由于gU为某个位置的绝对重力加速度值，将与其对应的位置记为C，则初始位置A00到位置C的距离记为heff_U，则
(8) 对比式(7)与式(8)，可得到
(9) 由式(9)可知，在利用同一套落体伺服控制系统对上、 下落体进行同步控制的过程中，heff_U与heff_D在对应的开始时间t1和结束时间tn的取值完全相同，即heff_U=heff_D，故将式(2)和式(3)代入式(1)，得
(10) 即利用式(1)进行重力垂直梯度计算时与g0的选取无关，仅取决于上、 下落体自由下落时重力加速度的计算和结构设计时所确定的两个落体光心之间的距离． 结构设计过程中，设上、 下落体光心间的水平距离为95 mm，若水平梯度按300—500 E(朱英，李卢玲，1982)计算，梯度测量误差为3—5 E，而本套梯度测量系统精度为100 E，因此水平梯度引入的误差可以暂时忽略，故式(1)中上、 下落体的光心间距即为上、 下落体光心间的垂直距离．
1.2 光路设计
激光干涉法重力垂直梯度测量系统的光路设计如图 2所示． 可以看到，激光器发出激光束入射至分光镜BS1的上表面，分别得到BS1上表面透射和反射两束同源激光，透射光入射至分光镜BS2的上表面，反射光经反射镜M反射后入射至分光镜BS3上表面． 分光镜BS2、 下落体P2和参考镜MS2等构成下落体P2的干涉测量光路，所形成的干涉条纹利用雪崩光电二极管(advanced photo diodes，简写为APD，下文分别用APD1和APD2表示上落体P1和下落体P2自由下落时形成的干涉条纹的接收器)接收并转换为电压信号被后端的高速数字化仪接收； 分光镜BS3、 上落体P1和参考镜MS1等构成P1的干涉测量光路，形成的干涉条纹被APD1接收并转换为电压信号被后端的高速数字化仪接收(吴琼等，2011)．
![]()
图 2 干涉法重力梯度测量原理Figure 2. Measuring principle of the gravity vertical gradient based on interferometry这套装置中，激光器、 分光镜(BS1，BS2，BS3)、 反射镜(M)、 参考镜(M1，M2)和光电接收器(APD1，APD2)均为刚性连接，真空舱中的P1和P2在同一套伺服电机控制系统作用下作自由下落运动，因此APD1和APD2接收到的干涉条纹所受到的地震动、 真空度、 气压、 极移和潮汐等环境干扰均保持相同． 源自这些因素的误差在测点重力梯度的差分计算时将被自动消除，不会影响最终测量结果的精度．
2. 测量系统设计
2.1 双落体伺服控制系统结构设计
基于激光干涉法的重力垂直梯度测量系统是利用一套电机伺服控制系统控制垂直方向间距为50 cm的两个落体作同步自由下落运动，故需要构建一个如图 3所示的真空系统，为落体的自由下落提供高真空环境，并为双落体伺服控制系统提供机械支撑．
真空系统安装在由3个支撑腿支撑的角架上，其中心旋转轴通过角架的质心，以确保角架完成水平调节后，真空系统的中心旋转轴为竖直状态． 该系统由上盖、 上二通底座、 上真空舱、 下真空舱和下二通底座等构成． 由于真空系统腔体较大，在构建真空环境时将分子泵直接安装在下二通底座上，并将其预抽至2×10-4 Pa以上时打开离子泵阀门，维持真空腔体内真空度优于5×10-4 Pa，满足落体自由下落对真空度的要求．
图 4为图 3所示真空系统内部安装的落体伺服控制系统． 图 4a显示的是落体伺服控制系统的整体结构，电机的输出力矩通过大气侧齿轮组和过真空传动机构驱动真空侧的齿条带动双落体作上下往复运动； 齿条经齿条运动导座约束后，可确保其沿竖直方向上下运动． 上托架内放置上落体P1，齿条通过万向联轴节驱动上托架，上托架沿上导轨作上下往复运动，对于下落体P2的驱动也采用同样的控制方式． 图 4b所示结构是为保证上、 下落体驱动的同步性而进行的特殊设计，由连接板、 连接块、 连接柱以及万向联轴节等构成． 连接板通过4个螺钉与上托架底端固定，末端与连接块固定； 连接块通过螺母锁定连接柱，三者构成“7”型结构； 连接柱通过万向联轴节与下托架固定． 该设计不仅可以保证上、 下托架在电机驱动下同步运动，还可抵消安装误差和制造误差所造成的径向力作用，使整套控制机构运行平稳可靠．
![]()
图 4 落体伺服控制系统设计(a)安装在真空舱内的落体伺服控制系统设计；(b)上、 下落体间刚性连接机构设计Figure 4. Design of the free-fall body servo control mechanism(a)Design of the free-fall body servo control mechanism in vacuum chamber;(b)Design of the rigid linkage between the up and down free-fall bodies2.2 双光路干涉测量系统设计
双光路干涉测量系统首先通过两个干涉光路测量单元分别采集上落体和下落体在自由下落过程中形成的激光干涉信号，再通过对其解算和差分运算得到地表重力垂直梯度．
依据图 2所示的测量原理设计双光路干涉测量系统的机械结构，如图 5所示． 激光器采用碘稳频激光系统，波长稳定度可达10-12，为整套测量系统提供长度基准． 高速数字化仪的时间基准由外部铷原子时钟提供，铷原子时钟输出频率的稳定度可达10-11，为整套仪器提供时间基准．
![]()
图 5 双光路激光干涉测量系统机构设计Figure 5. Design of the measuring structure of dual optical path measuring system based on laser interferometry干涉条纹的处理解算方面，由于上、 下落体自由下落的时间和位移信息可追溯到时间和长度基准，所以最后通过差分获得的重力垂直梯度值就具有了大动态范围、 无需标定和无零漂等特点； 构成双光路干涉测量系统所需的各个部件均刚性安装在双光路干涉测量系统的底板上，因此振动产生的误差属于共模误差，不会对最终的梯度测量结果产生影响．
光束垂直性调节方面，与激光干涉绝对重力仪不同，双光路干涉测量系统需要对两条测量光束进行垂直性调节． 首先，利用酒精液面提供的水平面和光学自准直仪，通过调整双光路干涉测量系统底板的支撑腿，调整入射上落体P1的测量光束的垂直性； 然后，同样利用酒精液面提供的水平面和光学自准直仪，通过调整反射镜M上的微调螺母，调整入射下落体P2的测量光束的垂直性． 这种调整方案的误差与光学自准直仪的误差相同，可以保证入射落体P1和P2的测量光束的垂直性误差小于0.2″．
2.3 测量系统构建与初步试验
目前，根据2.1和2.2节的设计已构建完成了一套可以正常工作的激光干涉法地表重力垂直梯度测量系统，如图 6a所示． 由于这套测量系统机构比较庞大，目前仅在实验室获取了初步的试验数据，如图 6b所示． 试验数据共有35组，每组进行16次测量.
![]()
图 6 激光干涉法地表重力垂直梯度测量系统(a)及其初步试验数据(b)Figure 6. The apparatus of the gravity vertical gradient measurement based on laser interferometry(a) and its preliminary test data(35 groups and 16 measurements per group)(b)在落体自由下落过程中，选取0.045—0.130 s时段的干涉信号进行计算． 对应落体自由下落距离为1—8 cm，生成的干涉信号是调频正弦波，频率为1.4—4.0 MHz(吴琼等，2012)． 考虑到采样频率引入的时间测量误差，选取采样频率为100 MHz，使得由采样引入的时间误差导致最终的测量误差小于1×10-8 m/s2．
图 7给出了单次测量中上落体自由下落时生成的干涉信号及其展开，可以看出，获取的干涉信号无明显干扰信号，信噪比高，可以满足高精度重力加速度值计算的要求．
![]()
图 7 实测上落体自由下落时得到的干涉条纹(a)及其展开(b)Figure 7. The interference fringes of the upper free-fall body during freely falling(a) and the expansion of the part of these fringes(b)3. 讨论与结论
在重力垂直梯度的测量过程中，潮汐、 极移、 气压、 真空度、 温度梯度、 涡流以及参考棱镜的振动等相较于明显的误差源，在绝对重力测量时不会影响重力垂直梯度的测量结果，但双落体自由下落的同步性控制、 参考点以及各个光学部件间的刚性和双测量光路的垂直性等则是影响其测量精度的重要因素．
2012年至今，在原有设计研发激光干涉重力仪的基础上，初步完成了激光干涉法地表重力垂直梯度测量系统的原理研究、 结构设计和系统构建等，并获取了本套测量系统的第一批试验数据． 从图 7所示的干涉信号可以看出，本套测量系统获取的上、 下落体在自由下落过程中所产生的干涉信号的信噪比高，干涉条纹清晰完整、 无畸变，完全满足后期的计算要求． 图 6b显示的是本次试验完成的35组测量结果的组平均值，试验中每组设定的测量次数为16次，共完成560次测量． 对测量获得的35组平均值再进行求平均计算，确定本次试验样机测量的测点的垂直向重力梯度为2886 E，精度为99 E．
2012年11月曾利用两台拉科斯特相对重力仪对本次试验所在测点的重力垂直梯度进行测量，得到的梯度值为2402 E(精度100 E)，对比分析初步确定本套梯度测量系统的测量准确度约为400 E．
本套梯度测量系统的精度和准确度不仅需要更多试验数据的测定，还需要制定更完备的测试精度和准确度的试验方案． 另外，针对伺服控制系统运行过程中的降噪问题、 数据处理算法和整套仪器的小型化设计等方面尚需进一步改进．
-
![]()
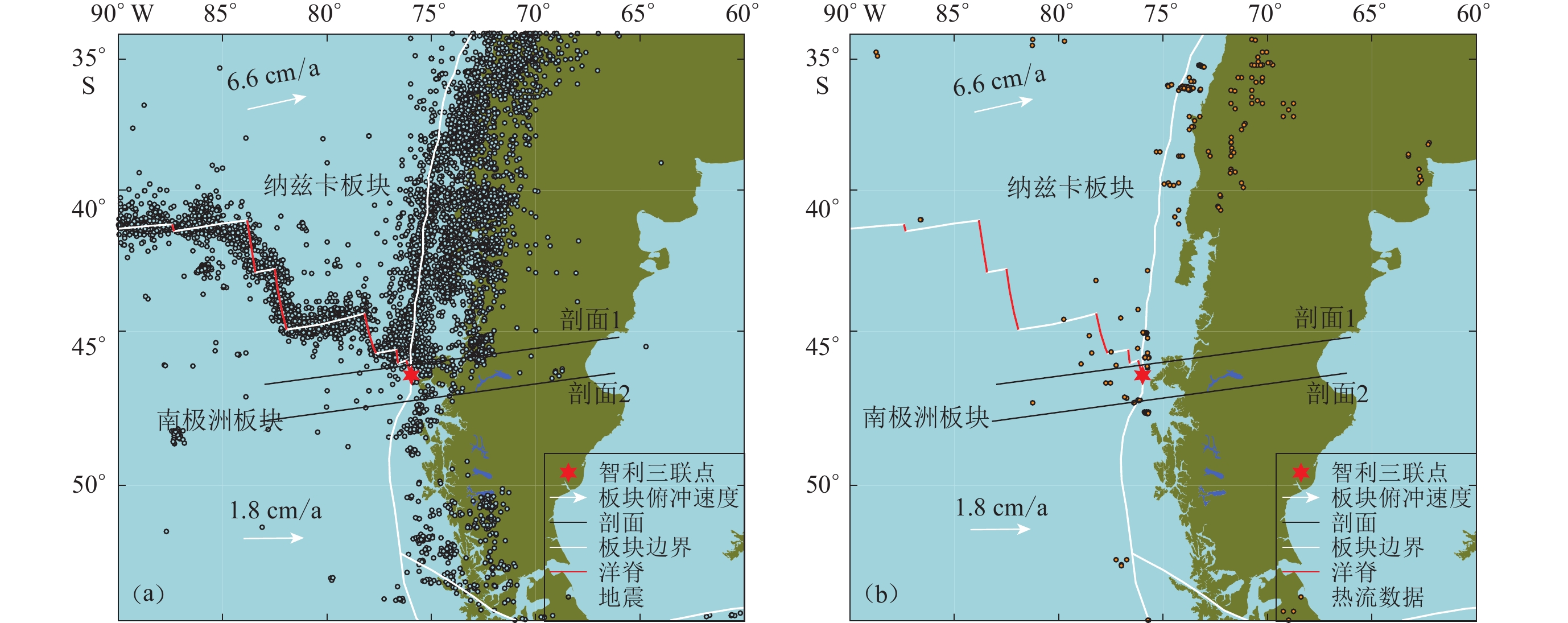
图 1 智利三联点区域构造背景及观测数据
（a） 智利三联点区域1906—2021年地震分布，数据来自国际地震中心（Bondár，Storchak，2011；Storchak et al，2017，2020）；（b） 智利三联点区域热流数据分布（Lucazeau，2019）
Figure 1. Geotectonic background of the Chile Triple Junction and the observed data
（a） Earthquake distribution in the area of CTJ from 1906 to 2021，the seismicity data are from the International SeismologicalCenter （Bondár，Storchak，2011；Storchak et al，2017，2020）；（b） The heat flow data in the area of CTJ （Lucazeau，2019）
![]()
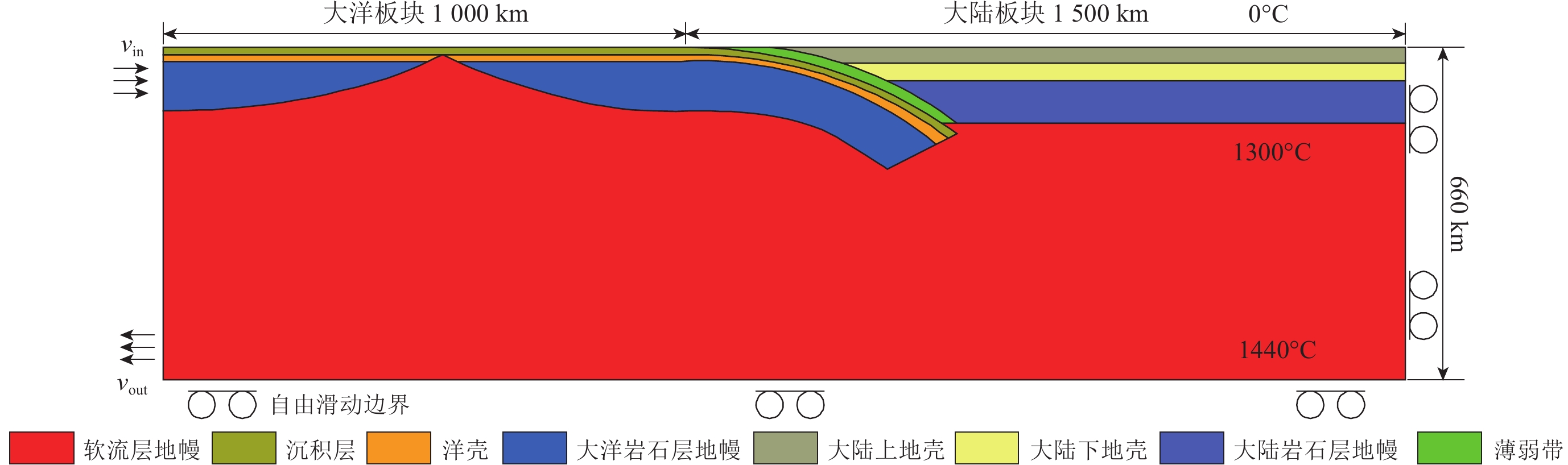
图 2 参考模型初始设置及边界条件
这些参数由干橄榄岩（Hirth，Kohlstedt，2004）的位错蠕变和扩散蠕变的流变实验获得
Figure 2. Initial setups and boundary conditions of the reference model
All these parameters come from the rheological experiments on dislocation creep and diffusion creep of dry olivine （Hirth，Kohlstedt，2004）
![]()
图 3 参考模型成分场（a）和黏滞系数η场的演化（b）
图中橙色实线为等温线，最低为100 ℃，最高为1 250 ℃
Figure 3. Evolutions of the material field （a） and the viscosity coefficient η field （b） of the reference model
Orange solid lines are isotherms，with a minimum of 100 ℃ and a maximum of 1 250 ℃
![]()
图 4 不同汇聚速率模型在俯冲汇聚量相同时的成分场（a）和黏滞系数场η（b）
Figure 4. The material field （a） and the viscosity field η （b） of different convergence rate models when the convergence distances are the same
![]()
图 5 不同初始俯冲角度模型在19.5 Ma时的成分场（a）和黏滞系数场η（b）
Figure 5. The material field （a） and the viscosity field η （b） of models of different initial slab dips at 19.5 Ma
![]()
图 6 对比模型孕震区宽度的演化
Figure 6. Evolution of the width of the seismogenic zone of contrast models
![]()
图 7 海沟附近地表热流分布
（a） 剖面1各模型热流结果；（b） 剖面1不同初始俯冲角度模型热流结果（汇聚速率＝4.2 cm/a）；（c） 剖面2不同初始俯冲角度模型热流结果（汇聚速率＝1.8 cm/a）
Figure 7. Surface heat flow in the vicinity of the trench
（a） Heat flow results of different models of profile 1；（b） Heat flow results of models with different initial slab dips of profile 1 （convergence rate＝4.2 cm/a）；（c） Heat flow results of models with different initial slab dips of profile 2 （convergence rate＝1.8 cm/a）
![]()
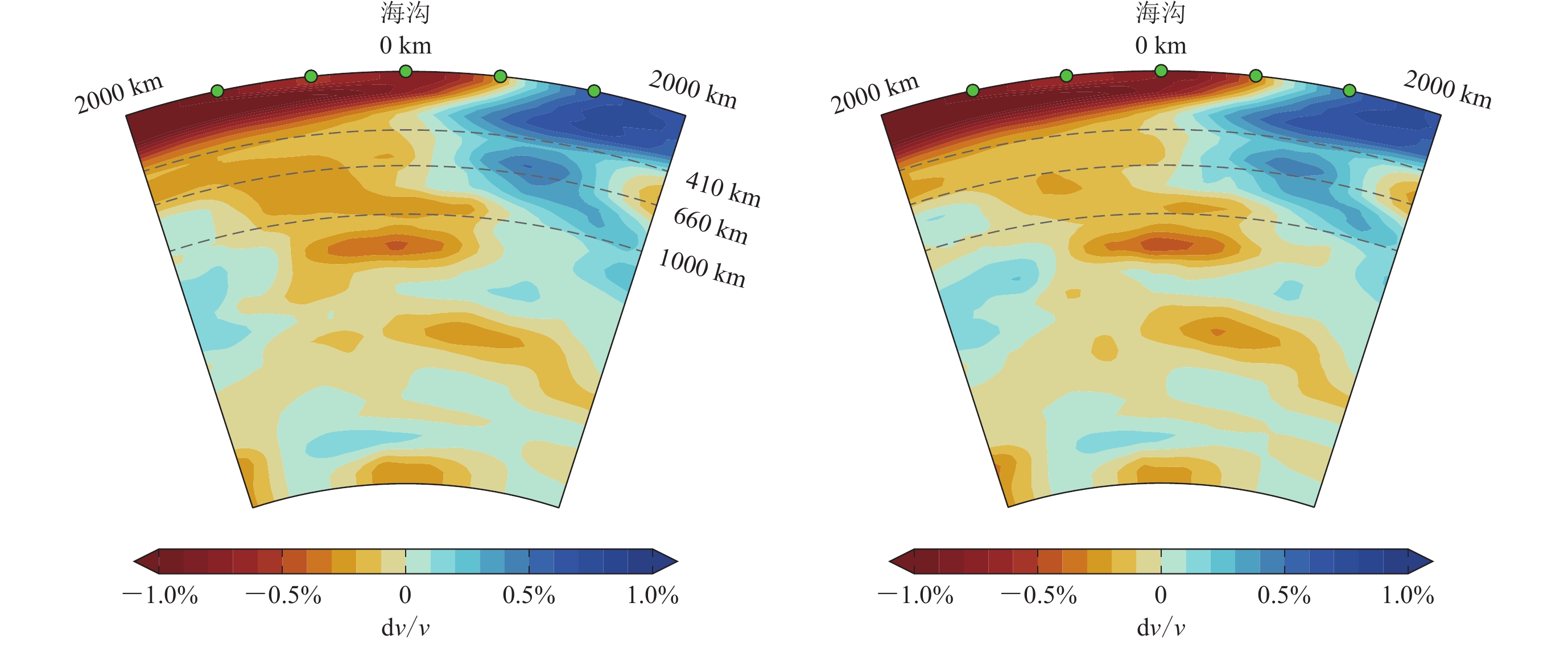
图 8 剖面1（左）和剖面2（右）的P波速度扰动（Simmons et al，2010）
Figure 8. Vertical cross sections of P wave velocity perturbations （Simmons et al，2010） along the profile 1 （left） and the profile 2 （right）
![]()
图 9 剖面1 （a）和剖面2 （b）的地震分布及孕震区
白色圆点为地震活动性数据。图a汇聚速率为4.2 cm/a，图b汇聚速率为1.8 cm/a
Figure 9. Earthquake distributions and seismogenic zones of the profile 1 （a） and the profile 2 （b）
Seismicity data are indicated by the white dots. The convergence rate of fig.（a） is 4.2 cm/a and 4.2 cm/a for fig.（b）
表 1 数值模型的相关参数
Table 1 Relevant parameters of numerical model
物质名称 厚度
/km热扩散率κ
/10−6 （m2·s−1）比热容Cp
/（J·kg−1· K−1）密度ρ
/（kg·m−3）热膨胀系数
α/10−5 K−1内摩擦角
φ/°黏聚力
C/106 Pa生热率A
/（W·m−3）流变
准则①晶粒大小
指数m地幔 660 0.989 750 3 300 2 20 20 干橄榄岩 3 大陆上地壳 20 1.21 750 2 800 2 20 20 10−6 湿石英 1 大陆下地壳 20 1.15 750 2 900 2 20 20 4×10−7 湿钙长石 1 岩石层地幔 0—87 9.87 750 3 300 2 20 20 干橄榄岩 3 沉积层 4 1.21 750 3 000 2 5 10 辉长岩 1 大洋地壳 8 1.15 750 3 100 2 20 10 辉长岩 1 薄弱带 1.21 750 3 300 2 0.03 1 辉长岩 1 
下载: 导出CSV
物质名称 前因子② （Pa−n·m−p·s−1） 应力指数n 活化能E/103 （J·mol−1） 活化体积V/10−6 （m3·mol−1） 扩散蠕变 位错蠕变 扩散蠕变 位错蠕变 扩散蠕变 位错蠕变 扩散蠕变 位错蠕变 地幔 2.37×10−15 6.52×10−16 1 3.5 375 530 4 13 大陆上地壳 1×10−50 8.57×10−28 1 4.0 0 223 0 0 大陆下地壳 1×10−50 7.13×10−18 1 3.0 0 345 0 0 岩石层地幔 2.37×10−15 6.52×10−16 1 3.5 375 530 4 18 沉积层 1×10−50 1.12×10−10 1 3.4 0 497 0 0 大洋地壳 1×10−50 1.12×10−10 1 3.4 0 497 0 0 薄弱带 1×10−50 1.12×10−10 1 3.4 0 497 0 0 注：① 流变准则：干橄榄岩来自Hirth和Kohlstedt （2004）；湿石英来自Gleason和Tullis （1995）；湿钙长石来自Rybacki （2006）；辉长岩来自Wilks和Carter （1990）。② 黏滞系数的前因子来自平面应变单轴试验结果（Naliboff，Buiter，2015；刘梦雪等，2019）.
下载: 导出CSV
表 2 参考模型孕震区宽度演化
Table 2 Evolution of the width of the seismogenic zone of the reference model
时间/Ma 闭锁区宽度/km
x（350℃）－x（100℃）过渡带宽度/km
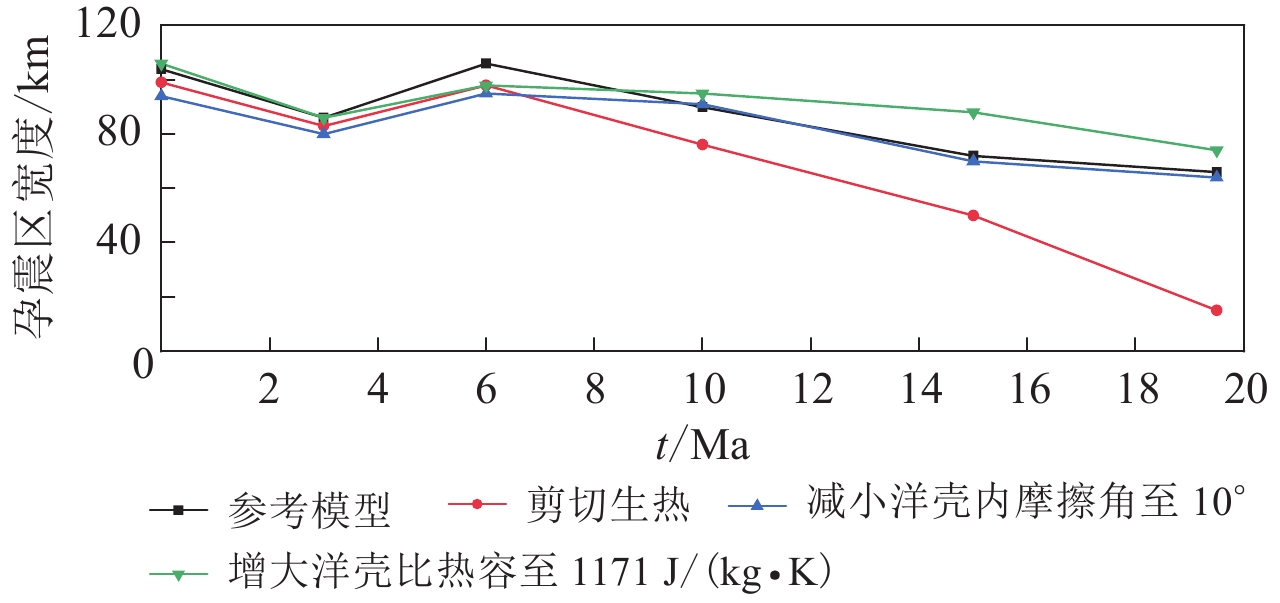
x（450℃）－x（350℃）孕震区宽度/km
x（350℃）－x（100℃） ＋0.5× ［ x（450℃） －x（350℃） ］洋脊与海沟横
坐标差/km0 86 36 104 −164 3 70 31 86 −60 6 89 34 106 −13 10 68 44 90 32 15 52 39 72 78 19.5 49 34 66 112
下载: 导出CSV
表 3 不同初始俯冲角度模型孕震区宽度演化
Table 3 Evolution of the width of the seismogenic zone of models of different initial slab dips
时间/Ma 孕震区宽度/km 洋脊与海沟横坐标差/km 15° 30° 45° 15° 30° 45° 0 111 104 66 −145 −164 −158 3 96 86 76 −67 −60 −36 6 85 106 74 −33 −13 8 10 94 90 60 14 32 36 15 90 72 51 46 78 67 19.5 80 66 52 77 112 92
下载: 导出CSV
表 4 部分模型孕震区深度演化
Table 4 Evolution of the depth of the seismogenic zone for some models
时间/Ma 参考模型 汇聚速率＝6.6 cm/a 俯冲角度＝45° 剪切生热 孕震区上边界
深度/km孕震区下边界
深度/km孕震区上边界
深度/km孕震区下边界
深度/km孕震区上边界
深度/km孕震区下边界
深度/km孕震区上边界
深度/km孕震区下边界
深度/km0 7 47 7 47 8 39 8 43 3 23 70 23 70 12 74 24 67 6 14 74 18 94 7 71 11 73 10 17 71 17 91 10 60 11 66 15 17 69 − − 5 51 9 51 19.5 19 70 − − 1 47 19 26
下载: 导出CSV
-
贾鸿瑞,魏东平. 2021. 智利三联点相关的板块相对运动及其地球动力学意义[J]. 地球物理学报,64(10):3567–3575. doi: 10.6038/cjg2021O0470 Jia H R,Wei D P. 2021. Relativemotion of plates related to the Chile triple junction and geodynamic significance[J]. Chinese Journal of Geophysics,64(10):3567–3575 (in Chinese).
李忠海,石耀霖. 2016. 三维板块几何形态对大陆深俯冲动力学的制约[J]. 地球物理学报,59(8):2806–2817. doi: 10.6038/cjg20160808 Li Z H,Shi Y L. 2016. Constraints of 3-D plate geometry on the dynamics of continental deep subduction[J]. Chinese Journal of Geophysics,59(8):2806–2817 (in Chinese).
刘梦雪,魏东平,史亚男. 2019. 俯冲初始时板块分界面形状对俯冲过程的影响[J]. 地球物理学报,62(1):78–87. doi: 10.6038/cjg2019L0717 Liu M X,Wei D P,Shi Y N. 2019. Effect of plate interface geometry on the evolution of subduction[J]. Chinese Journal of Geophysics,62(1):78–87 (in Chinese).
史亚男,魏东平,皇甫鹏鹏,李忠海,刘梦雪. 2019. 海洋板块俯冲作用下上覆大陆岩石层减薄机制的动力学模拟[J]. 地球物理学报,62(1):63–77. doi: 10.6038/cjg2019L0785 Shi Y N,Wei D P,Huangfu P P,Li Z H,Liu M X. 2019. Dynamics of thinning of overriding continental lithosphere induced by oceanic plate subduction:Numerical modeling[J]. Chinese Journal of Geophysics,62(1):63–77 (in Chinese).
沈晓明,张海祥,马林. 2010. 洋脊俯冲及其在新疆阿尔泰地区存在的可能证据[J]. 大地构造与成矿学,34(2):181–195. doi: 10.3969/j.issn.1001-1552.2010.02.004 Shen X M,Zhang H X,Ma L. 2010. Ridge subduction and the possible evidences in Chinese Altay,Xinjiang[J]. Geotectonica et Metallogenia,34(2):181–195 (in Chinese).
王振山,魏东平. 2018. 全球板块运动三联点形成与演化规律的研究进展[J]. 地球物理学进展,33(5):1834–1843. doi: 10.6038/pg2018BB0286 Wang Z S,Wei D P. 2018. Research progress on the formation and evolution of triple junctions of global plate motions[J]. Progress in Geophysics,33(5):1834–1843 (in Chinese).
徐佳静,王振山,王少坡,魏东平. 2019. 智利三联点南部扩张洋脊俯冲区域岩石层热结构的数值模拟[J]. 地球物理学报,62(12):4729–4737. doi: 10.6038/cjg2019M0592 Xu J J,Wang Z S,Wang S P,Wei D P. 2019. Numerical simulation of the lithospheric thermal structure in the subduction zone of the South Chile triple junction[J]. Chinese Journal of Geophysics,62(12):4729–4737 (in Chinese).
张克亮,魏东平. 2011. 双地震带的影响因素探讨[J]. 地球物理学报,54(11):2838–2850. doi: 10.3969/j.issn.0001-5733.2011.11.014 Zhang K L,Wei D P. 2011. On the influence factors of double seismic zones[J]. Chinese Journal of Geophysics,54(11):2838–2850 (in Chinese).
Agurto-Detzel H,Andreas R,Klaus B,Miller M,Iwamori H,Priestley K. 2014. Seismicity distribution in the vicinity of the Chile Triple Junction,Aysén Region,southern Chile[J]. J South Am Earth Sci,51:1–11. doi: 10.1016/j.jsames.2013.12.011
Assumpção M,Mei F,Andrés T,Julià J. 2013. Models of crustal thickness for South America from seismic refraction,receiver functions and surface wave tomography[J]. Tectonophysics,609:82–96. doi: 10.1016/j.tecto.2012.11.014
Bagherbandi M,Bai Y,Sjöberg L E,Tenzer R,Abrehdary M,Miranda S,Alcacer Sanchez J M. 2017. Effect of the lithospheric thermal state on the Moho interface:A case study in South America[J]. J South Am Earth Sci,76:198–207. doi: 10.1016/j.jsames.2017.02.010
Bangerth W, Dannberg J, Gassmoeller R, Heister T. 2020. ASPECT: Advanced solver for problems in Earth’s convection, user manual[BE/OL]. [2021-10-21]. https://www.math.clemson.edu/~heister/manual.pdf.
Bohm M,Lüth S,Echtler H,Bataille K,Group I W. 2002. The Southern Andes between 36° and 40° S latitude:Seismicity and average seismic velocities[J]. Tectonophysics,356(4):275–289. doi: 10.1016/S0040-1951(02)00399-2
Bondár I,Storchak D A. 2011. Improved location procedures at the International Seismological Centre[J]. Geophys J Int,186:1220–1244. doi: 10.1111/j.1365-246X.2011.05107.x
Bourgois J,Michaud F. 2002. Comparison between the Chile and Mexico triple junction areas substantiates slab window development beneath northwestern Mexico during the past 12−10 Myr[J]. Earth Planet Sci Lett,201:35–44. doi: 10.1016/S0012-821X(02)00653-2
Breitsprecher K,Thorkelson D J. 2009. Neogene kinematic history of Nazca-Antarctic Phoenix slab windows beneath Patagonia and the Antarctic Peninsula[J]. Tectonophysics,464(1/2/3/4):10–20. doi: 10.1016/j.tecto.2008.02.013
Contreras-Reyes E,Flueh E R,Grevemeyer I. 2010. Tectonic control on sediment accretion and subduction off south central Chile:Implications for coseismic rupture processes of the 1960 and 2010 megathrust earthquakes[J]. Tectonics,29:1–27.
Eakin C M,Obrebski M,Allen R M,Boyarko D C,Brudzinski M R,Porritt R. 2010. Seismic anisotropy beneath Cascadia and the Mendocino triple junction:Interaction of the subducting slab with mantle flow[J]. Earth Planet Sci Lett,297:627–632. doi: 10.1016/j.jpgl.2010.07.015
Fraters M,Thieulot C,van den Berg A,Spakman W. 2019. The geodynamic world builder:A solution for complex initial conditions in numerical modeling[J]. Solid Earth,(10):1785–1807.
Gleason G C,Tullis J. 1995. A flow law for dislocation creep of quartz aggregates determined with the molten salt cell[J]. Tectonophysics,247(1/2/3/4):1–23. doi: 10.1016/0040-1951(95)00011-B
Goddard A,Fosdick J C. 2019. Multichronometer thermochronologic modeling of migrating spreading ridge subduction in southern patagonia[J]. Geology,47(6):555–558. doi: 10.1130/G46091.1
Gresho P M,Lee R L,Sani R L,Maslanik M K,Eaton B E. 1987. The consistent Galerkin FEM for computing derived boundary quantities in thermal and/or fluids problems[J]. Int J Numer Meth Fl,7(4):371–394.
Guo C,Sun P,Wei D. 2021. Numerical simulation of the effects of wedge subduction on the lithospheric thermal structure and the seismogenic zone south of Chile Triple Junction[J]. Front Earth Sci,9:782458. doi: 10.3389/feart.2021.782458
Hamza V M,Dias F,Gomes A,Terceros Z. 2005. Numerical and functional representations of regional heat flow in South America[J]. Phys Earth Planet Inter,152:223–56. doi: 10.1016/j.pepi.2005.04.009
Heister T,Dannberg J,Gassmöller R,Bangerth W. 2017. High accuracy mantle convection simulation through modern numerical methods,II:Realistic models and problems[J]. Geophys J Int,210(2):833–851. doi: 10.1093/gji/ggx195
Hirth G, Kohlstedt D. 2004. Rheology of the upper mantle and the mantle wedge: A view from the experimentalists[C]// Geophysical Monograph Series. Washington D. C.: American Geophysical Union: 83–105.
Kirby S, Engdahl E R, Denlinger R. 1996. Intermediate-depth intraslab earthquakes and arc volcanism as physical expressions of crustal and uppermost mantle metamorphism in subducting slabs[C]// Geophysical Monograph Series. Washington D C: American Geophysical Union: 195–214.
Klotz J, Abolghasem A, Khazaradze G, Heinze B, Vietor T, Hackney R, Bataille K, Maturana R, Viramonte J, Perdomo R. 2006. Long-Term Signals in the Present-Day Deformation Field of the Central and Southern Andes and Constraints on the Viscosity of the Earth’s Upper Mantle[M]. Berlin: Springer: 65–89.
Kronbichler M,Heister T,Bangerth W. 2012. High Accuracy mantle convection simulation through modern numerical methods[J]. Geophys J Int,191(1):12–29. doi: 10.1111/j.1365-246X.2012.05609.x
Lagabrielle Y,Christèle G,René C M,Bourgois J,Martin H. 2000. Magmatic–tectonic effects of high thermal regime at the site of active ridge subduction:The Chile Triple Junction model[J]. Tectonophysics,326:255–268. doi: 10.1016/S0040-1951(00)00124-4
Lange D,Rietbrock A,Haberland C,Bataille K,Dahm T,Tilmann F,Flüh E R. 2007. Seismicity and geometry of the south Chilean subduction zone (41.5°S—43.5°S):Implications for controlling parameters[J]. Geophys Res Lett,34:L06311.
Lucazeau F. 2019. Analysis and mapping of an updated terrestrial heat flow data set[J]. Geochem Geophys Geosyst,20(8):4001–4024. doi: 10.1029/2019GC008389
Maksymowicz A,Eduardo C,Ingo G,Flueh E. 2012. Structure and geodynamics of the post-collision zone between the Nazca–Antarctic spreading center and South America[J]. Earth Planet Sci Lett,345-348:27–37.
Murdie R E,Prioe D J,Styles P,Flint S S,Agar S M. 1993. Seismic response to ridge-transform subduction:Chile triple junction[J]. Geology,21:1095–1098.
Naliboff J,Buiter S J H. 2015. Rift reactivation and migration during multiphase extension[J]. Earth Planet Sci Lett,421:58–67. doi: 10.1016/j.jpgl.2015.03.050
Oleskevich D A,Hyndman R D,Wang K. 1999. The updip and downdip limits to great subduction earthquakes:Thermal and structural models of Cascadia,south Alaska,SW Japan,and Chile[J]. J Geophys Res:Solid Earth,104:14965–14991. doi: 10.1029/1999JB900060
Richards F D,Hoggard M J,Cowton L R,White N J. 2018. Reassessing the thermal structure of oceanic lithosphere with revised global inventories of basement depths and heat flow measurements[J]. J Geophys Res:Solid Earth,123:9136–9161. doi: 10.1029/2018JB015998
Rose I,Buffett B,Heister T. 2017. Stability and accuracy of free surface time integration in viscous flows[J]. Phys Earth Planet Inter,262:90–100. doi: 10.1016/j.pepi.2016.11.007
Rybacki E. 2006. Influence of water fugacity and activation volume on the flow properties of fine-grained anorthite aggregates[J]. J Geophys Res:Solid Earth,200-201:1–9.
Scherwath M,Flueh E,Grevemeyer I,Tillman F,Contreras-Reyes E,Weinrebe W. 2006. Investigating subduction zone processes in Chile[J]. Eos Trans Am Geophys Un,87(27):265–272.
Scherwath M,Contreras-Reyes E,Flueh E R,Grevemeyer I,Krabbenhoeft A,Papenberg C,Petersen C J,Weinrebe R W. 2009. Deep lithospheric structures along the southern central Chile margin from wide-angle P-wave modelling[J]. Geophys J Int,179:579–600. doi: 10.1111/j.1365-246X.2009.04298.x
Shi Y,Wei D,Li Z,Liu M Q,Liu M. 2018. Subduction mode selection during slab and mantle transition zone interaction:Numerical modeling[J]. Pure Appl Geophys,175(2):529–548. doi: 10.1007/s00024-017-1762-0,175(2):529—548
Simmons N A,Forte A M,Boschi L,Grand S P. 2010. GyPSuM:A joint tomographic model of mantle density and seismic wave speeds[J]. J Geophys Res,115:B12310. doi: 10.1029/2010JB007631
Sisson V B,Pavlis T L,Roeske S M,Thorkelson D J. 2003. Introduction:An overview of ridge-trench interactions in modern and ancient settings[J]. Geol Soc Am Spec Papers,371:1–18.
Stein C A,Stein S. 1992. A model for the global variation in oceanic depth and heat flow with lithospheric age[J]. Nature,359(6391):123–129. doi: 10.1038/359123a0
Storchak D A,Harris J,Brown L,Lieser K,Shumba B,Verney R,Giacomo D D,Korger E I M. 2017. Rebuild of the bulletin of the International Seismological Centre (ISC),part 1:1964–1979[J]. Geosci Lett,4:32. doi: 10.1186/s40562-017-0098-z
Storchak D A,Harris J,Brown L,Lieser K,Shumba B,Di Giacomo D. 2020. Rebuild of the bulletin of the International Seismological Centre (ISC),part 2:1980–2010[J]. Geosci Lett,7:18. doi: 10.1186/s40562-020-00164-6
Tebbens S F,Cande S C,Kovacs L,Parra,J C,LaBrecque J L,Vergara H. 1997. The Chile ridge:A tectonic framework[J]. J Geophys Res:Solid Earth,102:12035–12059. doi: 10.1029/96JB02581
Tichelaar B W,Ruff L J. 1991. Seismic coupling along the Chilean subduction zone[J]. J Geophys Res,96(B7):11997. doi: 10.1029/91JB00200
Tetreault J L,Buiter S J H. 2012. Geodynamic models of terrane accretion:Testing the fate of island arcs,oceanic plateaus,and continental fragments in subduction zones[J]. J Geophys Res:Solid Earth,117(B8):B08403.
van der Hilst R,Hoop M. 2005. Banana-doughnut kernels and mantle tomography[J]. Geophys J Int,163:956–961. doi: 10.1111/j.1365-246X.2005.02817.x
Völker D,Ingo G,Michael S,Wang K,He J. 2011. Thermal control of the seismogenic zone of southern central Chile[J]. J Geophys Res,116:1–20.
Wei D, Seno T, 1998. Determination of the Amurian plate motion[C]// Mantle Dynamics and Plate Interactions in East Asia: Geodynamics Series. San Francisco: AGU: 337–346.
Wilks K R,Carter N L. 1990. Rheology of some continental lower crustal rocks[J]. Tectonophysics,182(1/2):57–77. doi: 10.1016/0040-1951(90)90342-6
Zhang K,Wei D. 2012. Correlation between plate age and layer separation of double seismic zones[J]. Earthquake Science,25:95–101. doi: 10.1007/s11589-012-0835-5
计量
- 文章访问数: 690
- HTML全文浏览量: 265
- PDF下载量: 172
