Determination of the radiated seismic energy for M≥6.0 earthquakes in the Qinghai-Xizang Plateau
-
摘要:
地震辐射能量主要由高频体波携带，与震源动态特征直接相关，能够有效地弥补地震矩和矩震级对震源动态过程和高频成分描述的不足，为地震应急和灾害评估提供更为全面的参考。本文使用自主研发的地震辐射能量测定软件测定了中国青藏高原自1990年以来M≥6.0浅源地震的地震辐射能量，并初步分析了中国青藏高原地区浅源地震的能量释放规律。研究结果表明：① 利用该软件测定的中国青藏高原地区的34例浅源地震所得的测定结果稳定可靠。在一般情况下，地震的矩震级MW 与能量震级Me并不相等，为了更全面地评估地震动效应，不仅需要考虑地震断层错动的静态特征，还需要考虑震源的动态特性。因此，在表示震源特性时，矩震级MW 和能量震级Me 各有特点，优势互补。② 改则地震和尼玛地震的能量震级分别为6.47和6.00，地震辐射能量分别为1.26×1014 J和0.25×1014 J。两次震源位置相近、矩震级相同的地震，所释放的能量相差5倍之多。为了探究改则地震与尼玛地震能量释放差异的原因，我们通过S变换对两次地震的波形进行了时频分析。结果表明，震源动态过程的不同导致了地震辐射能量释放过程的差异。因此能量震级和地震辐射能量等动态震源参数比矩震级更适合描述震源的动态过程和地震的潜在破坏性。③ 结合地震矩资料得到中国青藏高原地区浅源地震的平均能矩比为1.9×10−5，是全球浅源地震平均能矩比的1.6倍。能矩比的大小与震源机制有关，走滑型地震的平均能矩比高于倾滑型地震。④ 中国青藏高原浅源地震的能矩比分布存在区域特征，东部和西部平均能矩比分别为2.25×10−5和1.62×10−5，东部明显高于西部。能矩比的区域性差异与地质构造背景有关，地震辐射能量能够反映该地区的地质构造状态。同一区域内地震的能矩比也存在差别，中国青藏高原地区浅源地震的能矩比范围为5.03×10−6—4.80×10−5，反映了不同断层上发生的地震能量释放过程存在差异。因此，为全面反映地震的震源特性有必要进行能量震级和矩震级的联合测定。
Abstract:This study focuses on the radiated seismic energy of earthquakes with a magnitude of 6.0 or greater in Qinghai-Xizang Plateau of China, a region known for its seismic activity due to its unique tectonic setting. Radiated seismic energy, predominantly carried by highfrequency body waves, is a critical parameter that reflects the dynamic rupture process of an earthquake and complements the static characteristics described by seismic moment and moment magnitude. The accurate measurement of the radiated seismic energy is essential for a comprehensive understanding of earthquake dynamics, emergency response, and disaster assessment. The research utilized self-developed software to measure the radiated seismic energy of shallow earthquakes with a moment magnitude （MW） above 6.0 that occurred in QinghaiXizang Plateau since 1990. The study involved 34 earthquakes and aimed to analyze the energy release patterns in the region. It will help us to enhance our understanding of energy release patterns and their implications for seismic hazard assessment.
Introduction
The Qinghai-Xizang Plateau, often referred to as the “Roof of the World”, is not only a significant geographical feature but also a critical area for the study of seismic activity due to its location at the convergence of multiple tectonic plates. The region’s seismicity is influenced by the ongoing collision and compression of the Indian Plate with the Eurasian Plate, leading to a high potentiality for earthquake occurrences. The accurate measurement and analysis of radiated seismic energy are crucial for the potential hazards assessment posed by earthquakes, emergency response strategies forewarning, and guidance on the development of resilient infrastructure.
Methodology
The study employed a self-developed software to measure the radiated seismic energy of shallow earthquakes with a moment magnitude （MW） above 6.0. The software operates on the principles of point-source modeling and integrates the seismic moment rate spectrum over a specific frequency range to calculate the radiated energy. The methodology incorporates corrections for geometric spreading and frequency-dependent attenuation, ensuring the reliability and accuracy of the measurements. Data from the Incorporated Research Institutions for Seismology （IRIS） and the Global Seismic Network （GSN） were utilized to provide a robust dataset for the analysis.
Results
The research findings reveal several key insights into the radiated seismic energy and energy release patterns in the Qinghai-Xizang Plateau:
1） Stability and reliability of measurements: The radiated energy measurements for the 34 selected earthquakes were found to be stable and reliable, showing a high degree of consistency with that of the IRIS database. This validation confirms the effectiveness of the self-developed software in accurately determining radiated seismic energy.
2） Diversity in energy release: A significant variation in the energy release was observed between earthquakes, even those with similar MW and epicentral locations. For instance, the Garze and Nyima earthquakes, both with a moment magnitude of 6.4, exhibited substantial differences in their radiated energy and energy magnitude （Me）, underscoring the importance of considering both static and dynamic characteristics of seismic sources.
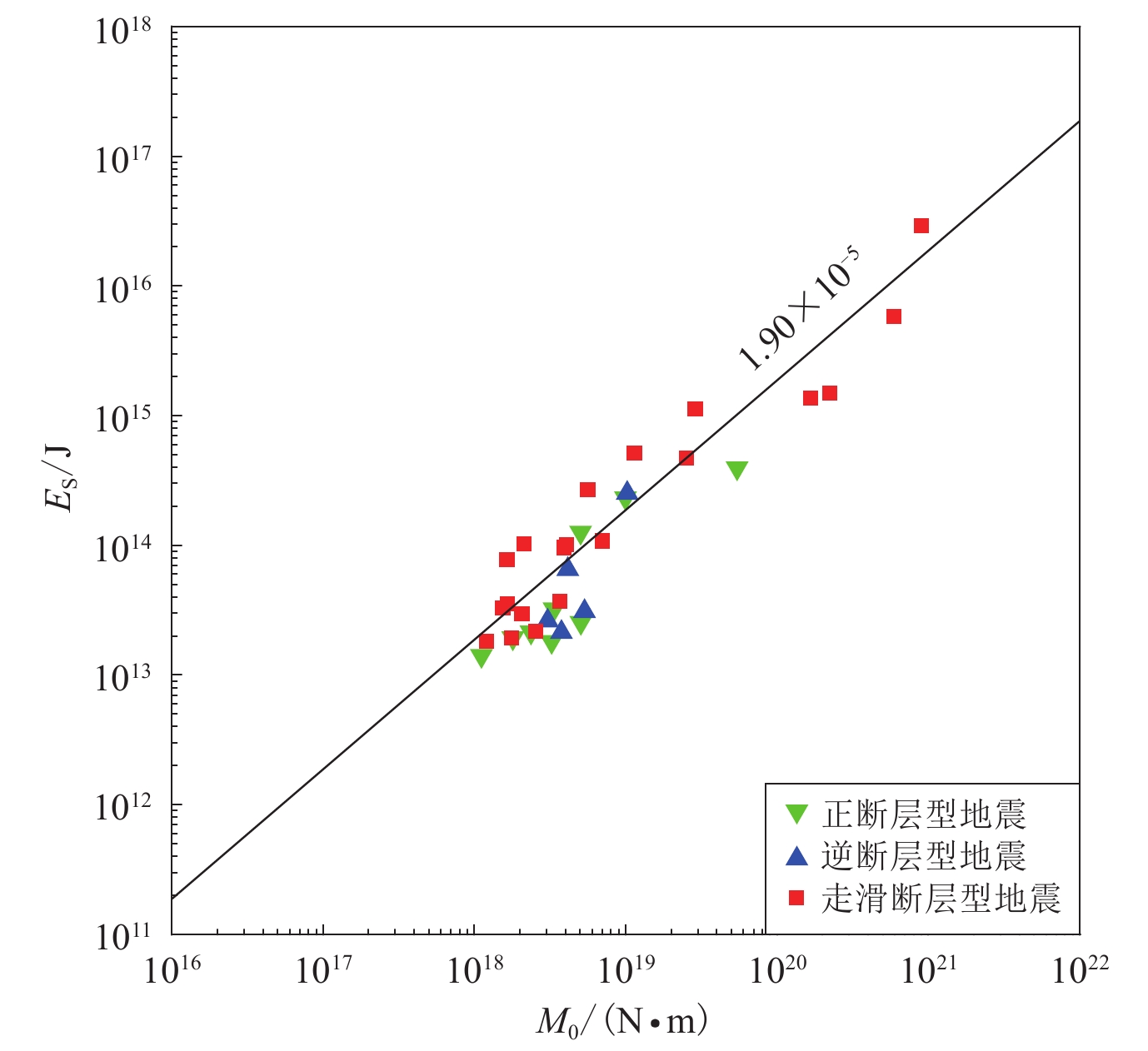
3） Regional characteristics of energy-to-moment ratio: The study identified distinct regional characteristics in the energy-to-moment ratio, with an average ratio （1.90×10−5） for Qinghai-Xizang Plateau which is 1.6 times higher than the global average. This suggests that earthquakes in this region are more energetically efficient, potentially leading to greater seismic hazards. A regional characteristic in the distribution of the energy-to-moment ratio was identified, with the eastern part of Qinghai-Xizang Plateau exhibiting a higher average ratio （2.25×10−5） than the western part （1.62×10−5）. This regional variation is believed to be linked to the geological structure background, indicating that radiated seismic energy can reflect the regioral geological state.
4） Mechanism-dependent energy release: The energy-to-moment ratio was found to be dependent on the focal mechanism of the earthquake, with strike-slip earthquakes exhibiting higher ratios compared to dip-slip earthquakes. This relationship provides valuable insights into the tectonic processes underlying seismic activity in the region. The study also found that within the same region, there is a significant range in the energy-to-moment ratio （from 5.03×10−6 to 4.80×10−5）, reflecting differences in energy release processes on various faults. The research concludes that the measurement of both energy magnitude and moment magnitude is necessary for fully understanding the source characteristics of an earthquake. The findings contribute to a better understanding of the potential destructiveness of earthquakes in Qinghai-Xizang Plateau and provide valuable insights for earthquake emergency response and disaster mitigation efforts in the region.
5） Geological significance: The regional variation in the energy-to-moment ratio appears to correlate with the underlying geological structure, indicating that the radiated seismic energy can serve as an indicator of the geological state and stress accumulation levels in the region.
Discussion
The research findings underscore the complexity of seismic energy release in Qinghai-Xizang Plateau and the need for a comprehensive assessment of earthquake hazards. The identification of regional characteristics in the energy-to-moment ratio provides valuable insights into the potentiality for seismic risk and the underlying tectonic processes. The research also highlights the importance of considering both the static （seismic moment and moment magnitude） and dynamic （radiated energy and energy magnitude） aspects of earthquakes for a more thorough understanding of their hazards.
The energy release patterns observed in this study have significant implications for the development of seismic hazard maps and the implementation of risk mitigation strategies. The higher energy release efficiency observed in Qinghai-Xizang Plateau suggests that earthquakes in this region may pose a greater threat to human settlements and infrastructure, necessitating enhanced preparedness and response capabilities.
Conclusion
The comprehensive analysis of radiated seismic energy in Qinghai-Xizang Plateau presented in this study contributes to a more nuanced understanding of earthquake dynamics in this seismically active region. The findings have significant implications for seismic hazard assessment and disaster mitigation strategies. By revealing the regional variations in energy release and their relationship with geological structures, this research aids in the development of targeted approaches to earthquake risk management in Qinghai-Xizang Plateau.
-
引言
地震时以地震波的形式传播的能量称为地震辐射能量，它是一个具有明确物理意义的重要震源参数，不仅可以衡量地震的“大小”，还可以反映地震的动态破裂过程。地震辐射能量的测定是地震定量化研究中的一个非常重要的课题，测定方法的发展主要分为两个阶段：地震学早期受限于模拟观测资料无法直接测定地震辐射能量，只能根据经验关系（Gutenberg，Richter，1956）间接估算；随着数字地震学的发展，宽频带地震仪器被广泛应用于台站并在全球范围内部署，使得利用数字观测资料直接测定地震辐射能量成为现实（Boatwright，Choy，1986；Kanamori et al，1993；Singh，Ordaz，1994；Choy，Boatwright，1995；Mayeda，Walter，1996；Boatwright et al，2002；Mayeda et al，2003；Morasca et al，2005；Boatwright，Seekins，2011）。但是，有关地震辐射能量的研究大多偏向测定方法，研究对象也以单个地震事件居多，对某个地区地震辐射能量规律的研究较少。
地震矩和地震辐射能量反映的是震源不同方面的特性：地震矩仅代表断层错动的“零频”（静态位错）成分的大小，与位错的时间历程无关；地震辐射能量则侧重震源辐射的高频成分，描述的是地震的动态破裂过程。研究表明，具有相同地震矩或矩震级的地震所释放的地震辐射能量可以相差几倍 （Choy，Boatwright，1995，2009；Choy et al，2006；王子博等，2021）。仅凭地震矩和矩震级难以全面评估地震的振动效应，地震辐射能量和能量震级更适合描述地震的潜在破坏性（Boatwright，Choy，1986；Bormann et al，2002；Choy，Kirby，2004）。应该结合两者的优势，为地震应急和防震减灾提供更为全面的参考。
青藏高原由于其特殊的地理位置而备受地震学家的关注。作为世界上著名的地震频发区，青藏高原有很大一部分位于中国境内，其中包括中国西藏全部和青海、新疆、甘肃、四川、云南的部分地区。青藏高原的自然历史发育极其年轻，受多种因素的共同影响，形成了全世界温度最高、最年轻而水平地带性和垂直地带性紧密结合的自然地理单元。同时，青藏高原地区是世界上发生陆内地震的主要地区，不但地震强度大、频次高，而且规律性强。自1972年至2022年6月，青藏高原发生的M＞6.0地震就多达86次，历史最高震级达M8.5 （1950年察隅地震），其中发生在中国境内的有57个，占全部事件的66%。本文测定中国青藏高原1990年至今MW≥6.0浅源地震的辐射能量，尝试分析该区域的地震辐射能量规律。以期为了解该地区地震的潜在破坏性和致灾机理及该地区的防震减灾工作提供参考。
1. 数据
我们从美国地震学联合研究会（Incorporated Research Institutions for Seismology，缩写为IRIS）查询到1990年以来MW≥6.0的地震事件3 958例，发生在青藏高原地区的有48例，其中有34例位于中国境内（图1）。我们从IRIS数据中心（Data Management Center，缩写为DMC）的全球地震台网（Global Seismic Network，缩写为GSN）下载了34个地震事件的宽频带数据，共计1 779个台站。选择其中信噪比较好的垂直向（BHZ）记录用于测定中国青藏高原浅源地震的辐射能量和能量震级。
![]()
图 1 中国青藏高原MW≥6.0浅源地震分布Figure 1. Earthquakes with MW≥6.0 occurred in Qinghai-Xizang Plateau in China2. 地震辐射能量快速测定方法
地震波在传播过程中受路径衰减的影响非常明显，虽然P波携带的地震辐射能量比例较小，但受到的衰减影响比S波要小的多；且P波传播速度快，能够更早被台站接收。因此，远场P波常被用于地震辐射能量的测定（Boatwright，Choy，1986；Choy，Boatwright，1995；Tajima，Tajima，2007；Di Giacomo et al，2008，2010；Allmann，Shearer，2009；王子博等，2021）。本节简单介绍和回顾了在点源震源模型下，使用远场P波资料测定地震辐射能量的理论基础和所作的一些假设。地震辐射能量测定原理的详细信息可参考前人文献（Haskell，1964；Rudnicki，Freund，1981；Vassiliou，Kanamori，1982；Boatwright，Choy，1986；Venkataraman，Kanamori，2004a，b；Di Giacomo et al，2010）。
在频率域对地震矩率导数的谱$ \widehat {\ddot M} （ f ） $的平方求积分，可以得到地震辐射能量ES，即
$$ E_{\text{S }} {\text{＝}} \left[ {\frac{2}{{15\text{π} \rho {\alpha ^5}}} + \frac{1}{{5\text{π} \rho {\beta ^5}}}} \right]{\int_{{f_1}}^{{f_2}} {\left| {\widehat {\ddot M} （ f ） } \right|} ^2}{\mathrm{d}}f \text{，} $$ (1) 式中，α和β分别为P波和S波的速度，ρ为震源处介质的密度，f为频率，f1和f2分别为积分的下限和上限。式中只有地震矩率导数的谱一个未知量，因此，求地震辐射能量的问题就转化为了求地震矩率导数的谱的问题。地震矩率实际上与震源时间函数有关，震源时间函数描述震源的时间历史，它可以是地震断层的滑动量或滑动率的时间历史，也可以是震源地震矩或地震矩率的时间历史。如果用地震矩描述震源，不考虑体力和应力的间断性，在一个分界面Σ两侧的位移间断uj$ （ $ξ， τ$ ） $所引起的弹性位移可简单地表示为（陈运泰，顾浩鼎，1990）：
$$ u_{i} （ {x {\text{，} }t} ） {\text{＝}} \iint_{\varSigma} {G_{ij {\text{，} }k} （ {x {\text{，} }t\text{；} \xi {\text{，} } \tau } ） } * \dot {\boldsymbol{m}}_{jk} （ {\xi {\text{，} } \tau } ） {\mathrm{d}} { \varSigma }\text{，} $$ (2) 式中，Gij， k是格林函数在断层面上的点ξ在k方向的偏导数，表示断层面上的点ξ与观测点x之间的路径效应，$ \dot {\boldsymbol{m}}_{jk} $为断层面上的点ξ的地震矩率张量，“*”表示时间域的褶积。
当断层尺度远小于所考虑的波长时，可将震源看作点源，此时，式（2）可简化为（Lay，Wallace，1995）：
$$ u_{i} （ t ） {\text{＝}} {G_{jk {\text{，} }t}} （ t ） *{ \dot {\boldsymbol{m}}_{jk}} （ t ） \text{，} $$ (3) 将式（3）转换到频率域并求$ \dot {\boldsymbol{m}}_{jk} $，可得：
$$ \dot {\boldsymbol{m}}_{jk} （ f ） {\text{＝}} \frac{{u_{i} （ f ） }}{{G_{ij {\text{，} }k} （ f ） }} \text{，} $$ (4) 对式（4）再次求导可得$ \widehat {\ddot M} （ f ） $。由式（4）可知，地震矩率导数实际上是震源时间函数的一种表达形式，可以通过实际波形的格林函数解卷积得到，这一过程实际上就是校正观测记录的过程。地震辐射能量的计算需要在一个频率比较宽的范围对因地震波由震源到接收处的传播过程中的几何扩散（geometrical spreading）以及频率依赖的衰减（frequency-dependent attenuation）进行校正。而校正频率大于1 Hz的频带时，不仅需要详细了解整个传播路径的精细结构和衰减特性，还需要详细了解台站下方的精细结构和衰减特性，但这通常是不可能的。因此，一般仅计算震级大于5的地震的地震辐射能量，且使用的是震中距大于20°的远震记录，以便通过假设的一维层状结构来合理准确地模拟地球的过滤效果（the Earth filter effects）。本文使用AK135一维速度模型，其中的Q值是由周期最小为1 s的数据获得的（Montagner，Kennett，1996）。对于更短的周期，衰减函数并不可靠。因为与实际数据相比，它们的频谱衰减程度太大。所以，用AK135模型计算更高频的格林函数并不合适。1 Hz的限制意味着，目前我们的程序仅适用于MW＞5.5地震。但地震辐射能量的测定并不会因此受限，因为强震至特大地震的拐角频率通常都落在我们使用的频带内。并且地震辐射能量与速度的平方成正比，计算中未考虑的震源频谱部分（f＜f1和f ＞f2）不会显著影响能量震级的测定，最差的情况下也仅约为0.2 （Di Giacomo，2010）。
目前，矩震级MW被广泛用于评估地震的“大小”，矩震级由地震矩M0导出，是一个稳定且统一的衡量地震规模的震级标度（Hanks，Kanamori，1979）。地震矩描述了震源破裂前后应力释放的大小，与构造形变直接相关，描述的是震源的静态特征；地震辐射能量ES与地震破裂过程的复杂性密切相关，描述的是地震的动态过程（Husseini，1977；Kanamori et al，2020）。与地震矩M0可以导出矩震级MW类似，由地震辐射能量也可以导出能量震级Me （Choy，Boatwright，1995）：
$$ M_{\mathrm{e}} {\text{＝}} \frac{2}{3} （ {\lg {E_{\mathrm{S}}} {\text{－}} 4.4} ） . $$ (5) 3. 测定结果分析
3.1 地震辐射能量测定结果分析
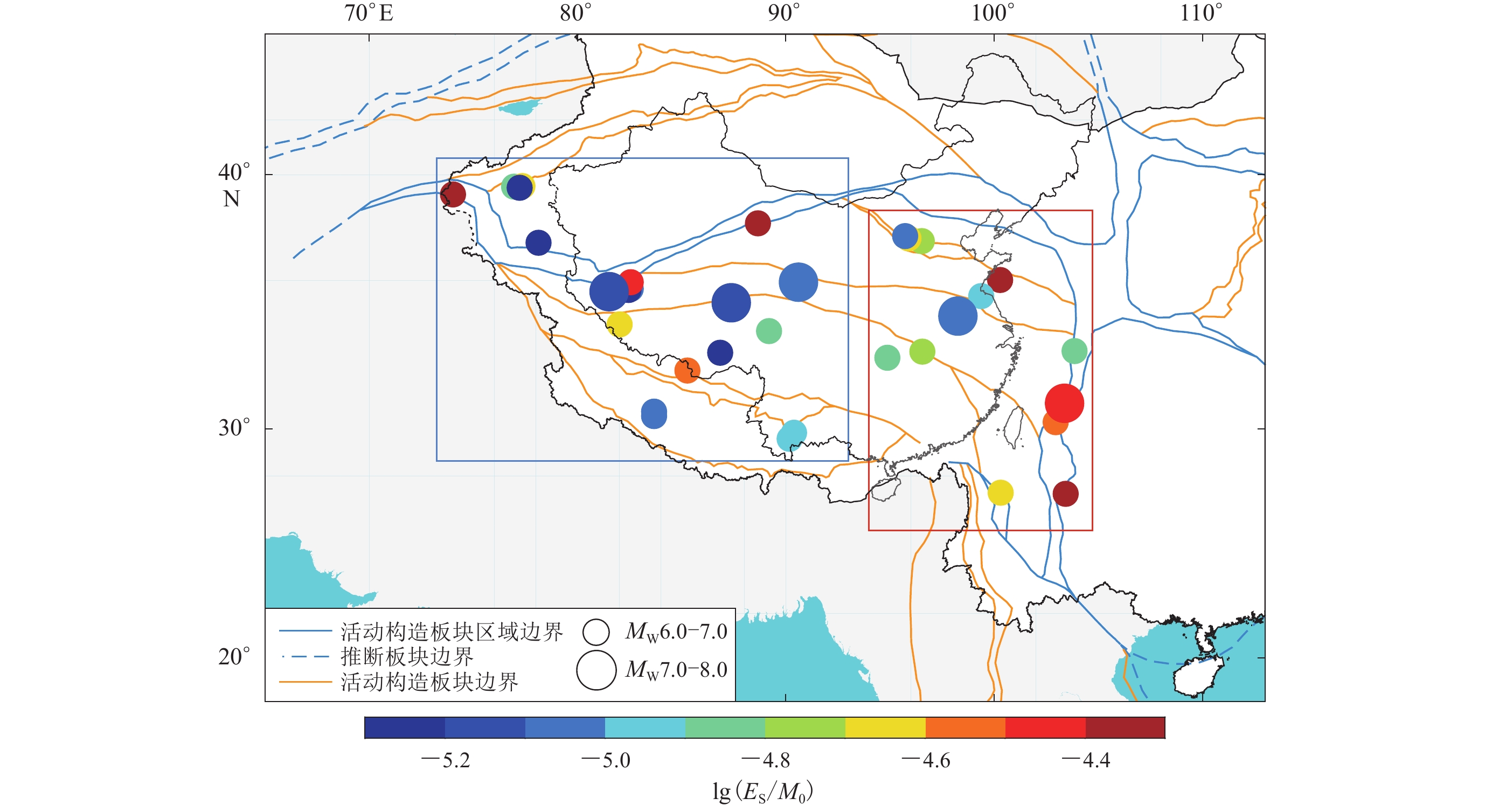
基于上述方法，我们使用自主研发的地震辐射能量快速测定程序（孔韩东等，2022）测定了1990—2021年发生于中国青藏高原地区的34例浅源地震的辐射能量。图1显示了34例地震事件的震源位置和相应的震源机制，震级范围为MW6.0—7.9，详细参数列于表1。为了便于比较，我们通过式（2）计算出的能量震级来描述地震辐射能量ES的大小。
表 1 中国青藏高原浅源地震的震源参数Table 1. Source parameters of shallow earthquakes in Qinghai-Xizang Plateau in China发震日期
a-mo-d震中位置 震源
深度
/kmM0
/（1018 N·m）MW MS ES
/（1013J）Me I Me 震源机制
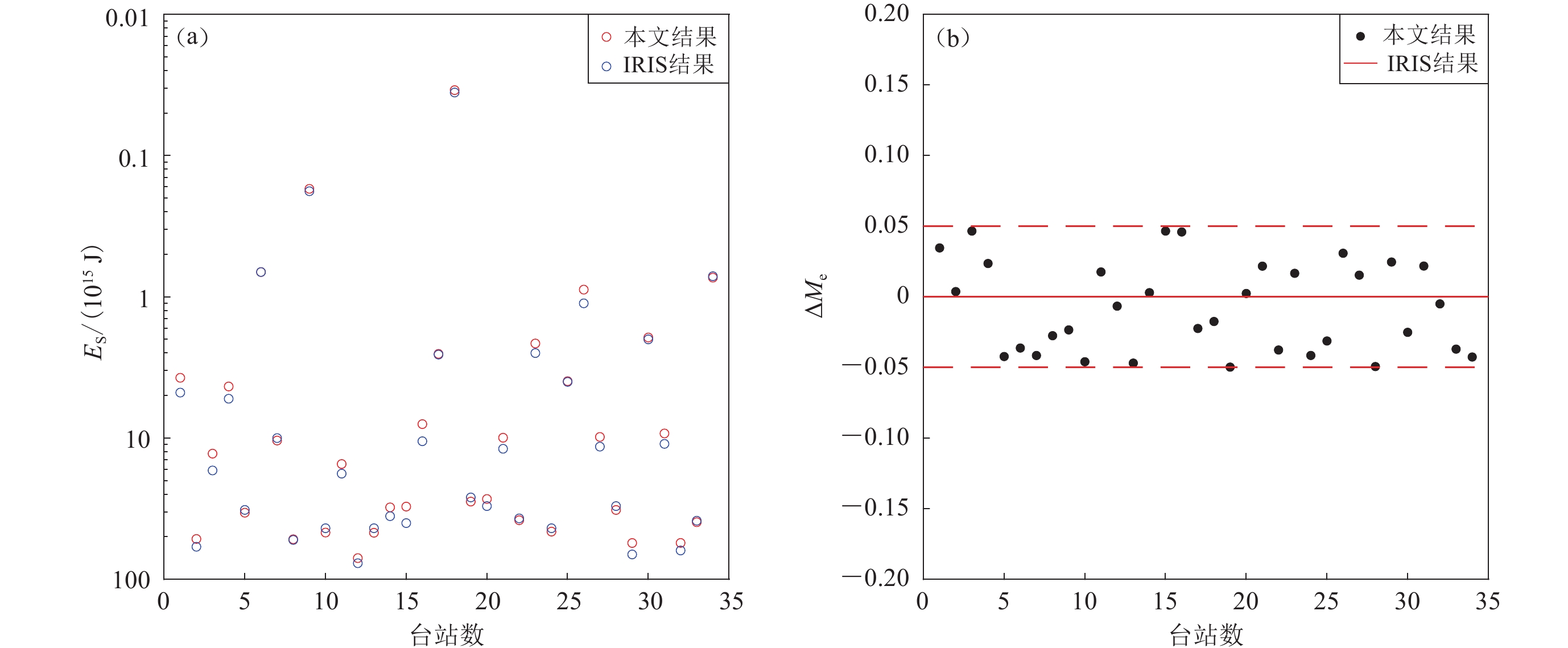
类型参考位置 东经/° 北纬/° 1 990-04-26 100.28 36.02 10.0 5.61 6.4 6.9 26.7 6.65 6.68 走滑型 青海共和 1 992-07-30 90.18 29.57 31.4 1.79 6.1 5.8 1.93 5.92 5.92 正断型 西藏尼木 1 993-10-02 88.66 38.17 14.1 1.64 6.1 6.3 7.76 6.28 6.33 走滑型 新疆若羌 1 996-02-03 100.29 27.29 10.0 9.94 6.6 6.5 23.2 6.62 6.64 正断型 云南丽江 1 997-04-11 96.95 39.56 20.0 2.06 6.1 6.1 2.96 6.09 6.05 走滑型 新疆伽师 1 997-11-08 87.37 35.12 38.1 223 7.5 7.9 150 7.22 7.18 走滑型 西藏尼玛 1 998-08-27 77.34 39.58 33.0 3.89 6.3 6.4 9.61 6.43 6.39 走滑型 新疆伽师 2 000-09-12 99.37 35.37 12.0 1.76 6.1 6.3 1.92 5.95 5.92 走滑型 青海兴海 2 001-11-14 90.59 35.93 11.0 590 7.8 8.0 582 7.60 7.58 走滑型 昆仑山口 2 003-02-24 77.21 39.52 26.2 3.74 6.3 6.3 2.14 6.00 5.95 逆断型 巴楚—伽师 2 003-04-17 96.51 37.52 15.0 4.12 6.3 6.3 6.55 6.26 6.28 逆断型 青海德令哈 2 004-03-27 89.18 33.99 9.0 1.11 6.0 5.8 1.41 5.84 5.83 正断型 西藏班戈 2 004-07-11 83.67 30.72 8.1 2.36 6.2 6.2 2.14 6.00 5.95 正断型 西藏仲巴 2 005-04-07 83.66 30.52 14.7 3.35 6.3 6.1 3.23 6.07 6.07 正断型 西藏仲巴 2 007-05-05 82.03 34.27 14.2 1.54 6.1 6.0 3.27 6.03 6.08 走滑型 日土—改则 2 008-01-09 85.26 32.4 27.7 5.02 6.4 6.4 12.6 6.42 6.47 正断型 西藏改则 2 008-03-20 81.51 35.55 10.0 54.3 7.1 7.3 39.5 6.82 6.80 正断型 新疆于田 2 008-05-12 103.37 31.06 7.6 897 7.9 8.1 2910 8.06 8.04 逆冲型 四川汶川 2 008-05-12 103.63 31.24 11.5 1.65 6.1 6.1 3.55 6.15 6.10 走滑型 四川汶川 2 008-10-06 90.38 29.84 6.4 3.65 6.3 6.3 3.70 6.11 6.11 走滑型 西藏当雄 2 008-11-10 95.89 37.62 0.1 4.06 6.3 6.4 10.1 6.38 6.40 走滑型 青海海西 2 009-08-28 95.76 37.67 12.1 3.04 6.3 6.2 2.62 6.05 6.01 逆断型 青海海西 2 010-04-13 96.75 33.19 13.8 25.3 6.9 7.0 46.8 6.83 6.85 走滑型 青海玉树 2 012-08-12 82.54 35.65 14.0 2.55 6.2 6.3 2.18 6.00 5.96 走滑型 新疆于田 2 013-04-20 103.02 30.27 18.0 10.2 6.6 6.8 25.3 6.70 6.67 逆断型 四川雅安 2 014-02-12 82.58 35.88 4.1 28.7 6.9 6.9 113 7.07 7.10 走滑型 新疆于田 2 014-08-03 103.43 27.25 10.0 2.12 6.2 6.2 10.2 6.39 6.41 走滑型 云南鲁甸 2 015-07-03 78.12 37.47 19.0 5.33 6.4 6.4 3.10 6.11 6.06 逆断型 新疆皮山 2 016-10-17 94.87 32.91 32.1 1.20 6.0 5.9 1.81 5.88 5.90 走滑型 青海杂多 2 016-11-25 74.02 39.23 17.0 11.3 6.6 6.6 51.6 6.90 6.87 走滑型 新疆阿克陶 2 017-08-08 103.86 33.19 9.0 6.98 6.5 6.5 10.8 6.40 6.42 走滑型 四川九寨沟 2 020-06-25 82.42 35.59 10.0 3.23 6.3 6.3 1.81 5.91 5.91 正断型 新疆于田 2 020-07-22 86.87 33.15 10.0 5.04 6.4 6.3 2.54 6.04 6.00 正断型 西藏尼玛 2 021-05-21 98.24 34.59 10.0 166 7.4 7.3 137 7.20 7.16 走滑型 青海玛多 注：经纬度信息及MeI来自IRIS；M0，MW和MS来自GCMT；ES和Me为本文测定的地震辐射能量和能量震级。 由表1可以看出，我们测定了34个地震事件的地震辐射能量和能量震级，并分别与IRIS的测定结果进行了比较。图2比较了本文能量震级测定结果与IRIS结果，从图中可以看出，两者的误差在±0.05之间，相差很小，表明本文的测定结果十分稳定、可靠。而该误差可能来源于所使用的台站不同或数据处理细节上的不同。
![]()
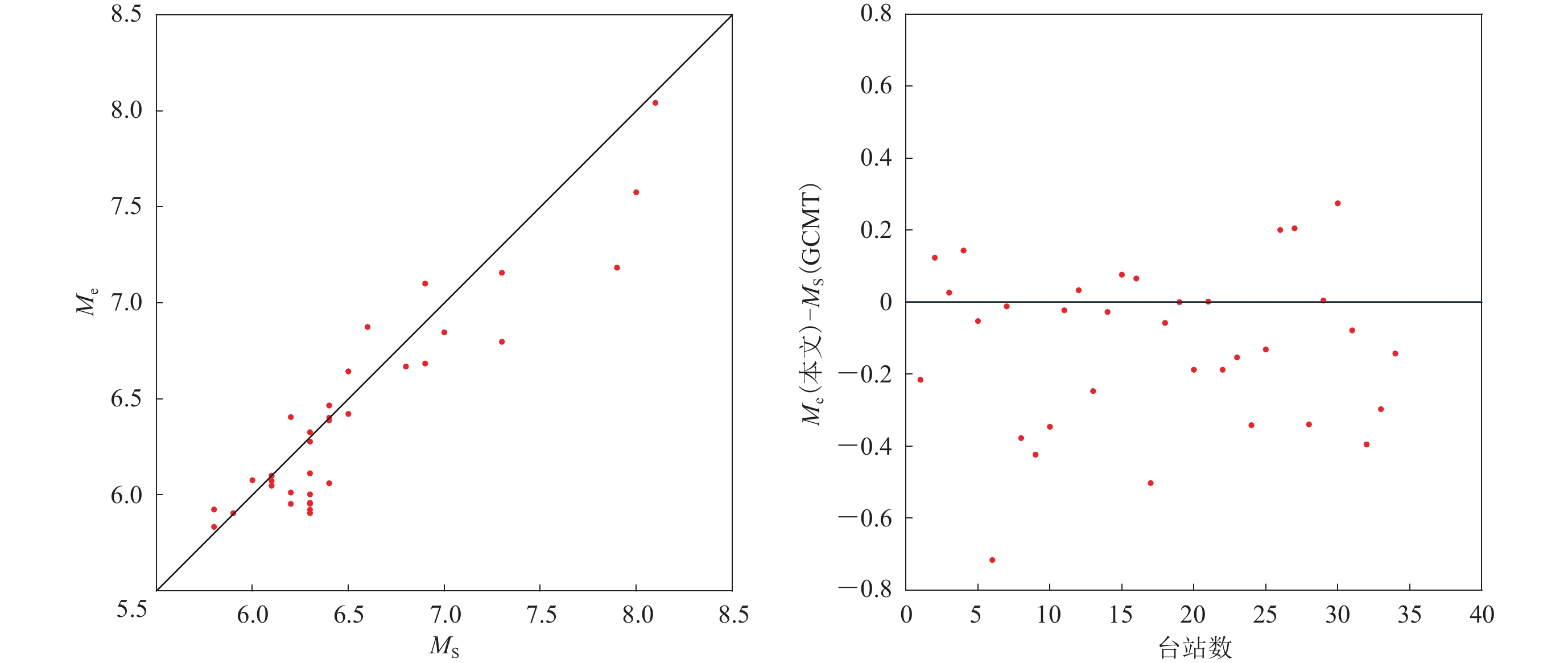
图 2 本文测定的地震辐射能量（a）和能量震级（b）与IRIS结果的对比Figure 2. Comparison of radiated seismic energy （a） and Me （b） between IRIS and this paper图3给出了本文测定的能量震级与GCMT面波震级的关系图。其中，12个事件的能量震级高于面波震级，22个事件的矩震级大于能量震级。能量震级与面波震级相差最大的为1997年11月8日西藏尼玛地震，震级差达到了0.72。如上所述，地震事件的面波震级与能量震级一般不相等。面波震级一般是在特定周期（T＝20 s）下测定的震级标度，代表的是震源某一方面的特征，且会受震级饱和效应的影响。当震级达到一定大小后，面波震级就不再增加，此时只有不受震级饱和效应影响的震级标度才能反映地震的“真实大小”。矩震级和能量震级均不受震级饱和效应的影响，分别反映了震源的静态特征和动态特征，因此被更为广泛的用于衡量“地震大小”。
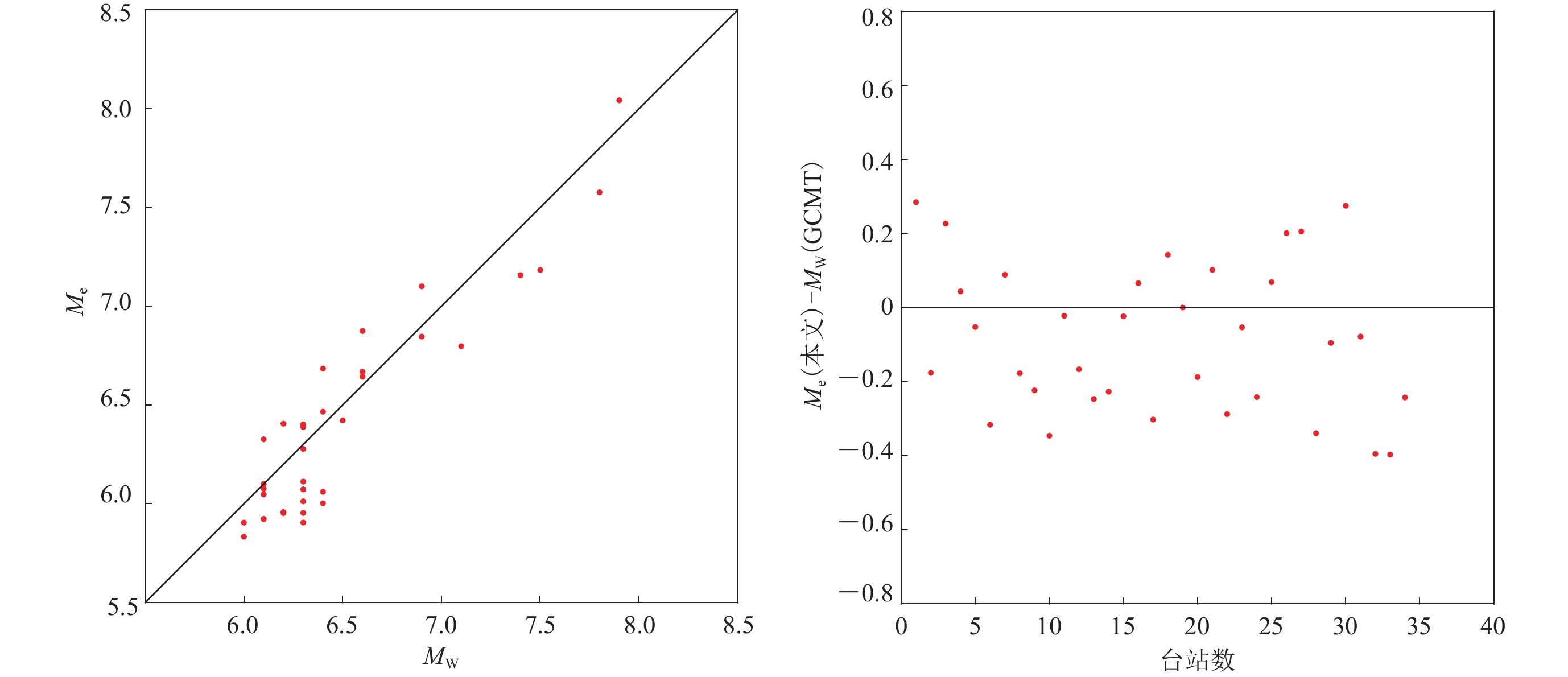
图4给出了本文测定的能量震级与GCMT矩震级的关系。从图中可以看出，12个事件的能量震级大于矩震级，而其它22个事件的能量震级均小于矩震级。为判定地震事件的辐射能量是否异常高，可以使用等效震级差ΔM （Choy，2012）作为参考标准。当ΔM＞0时，地震辐射能量异常高；当ΔM＜−0.5时，地震辐射能量异常低（Choy，2012）。中国青藏高原浅源地震的平均等效震级差为−0.09，远高于全球浅源地震的平均等效震级差−0.36 （Choy，2012），说明中国青藏高原属于能量释放较高的区域。一般情况下，地震事件的矩震级和能量震级并不相等，为了全面描述地震的震源特性，有必要在地震发生后联合测定矩震级和能量震级。
3.2 代表性震例
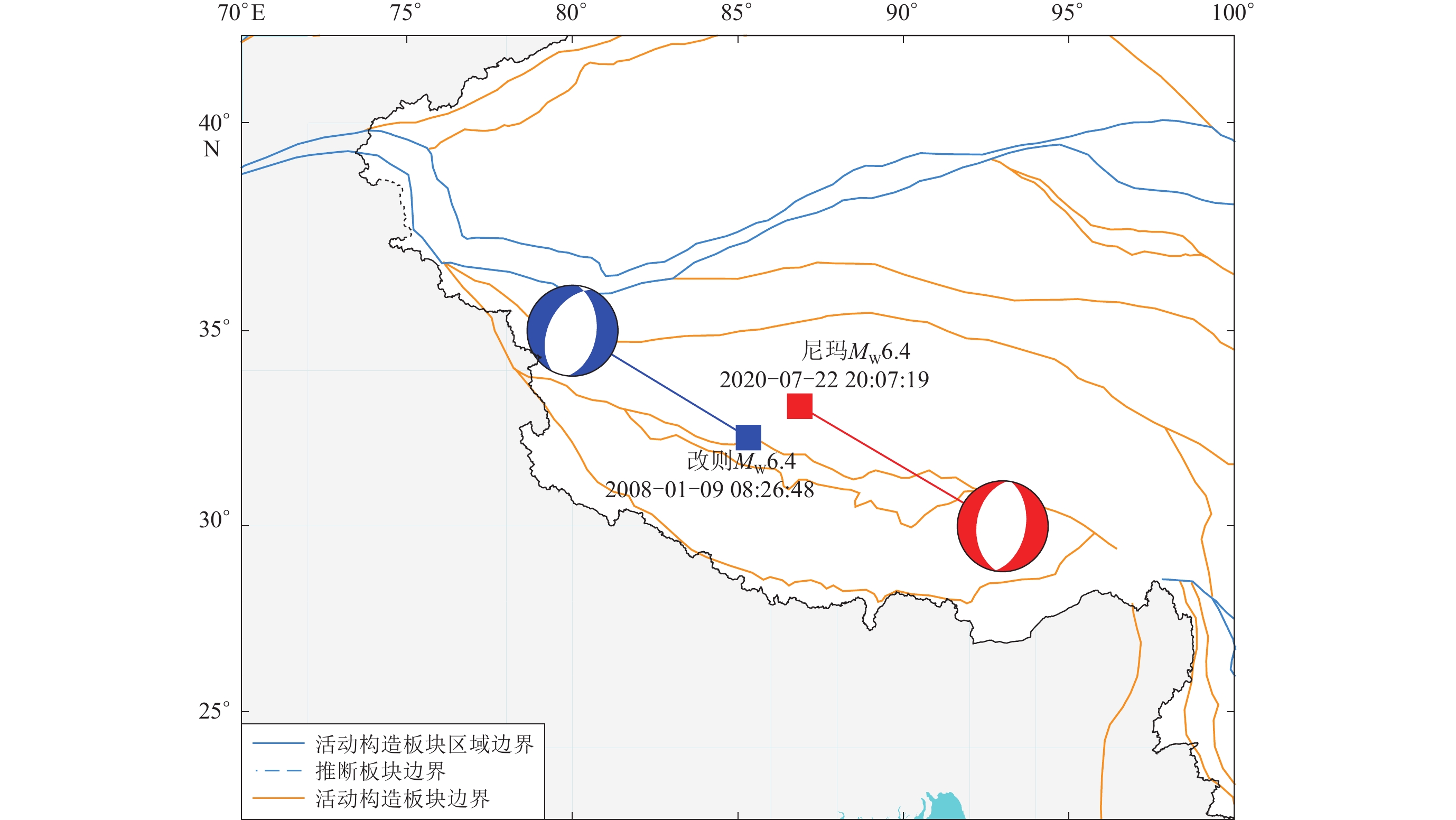
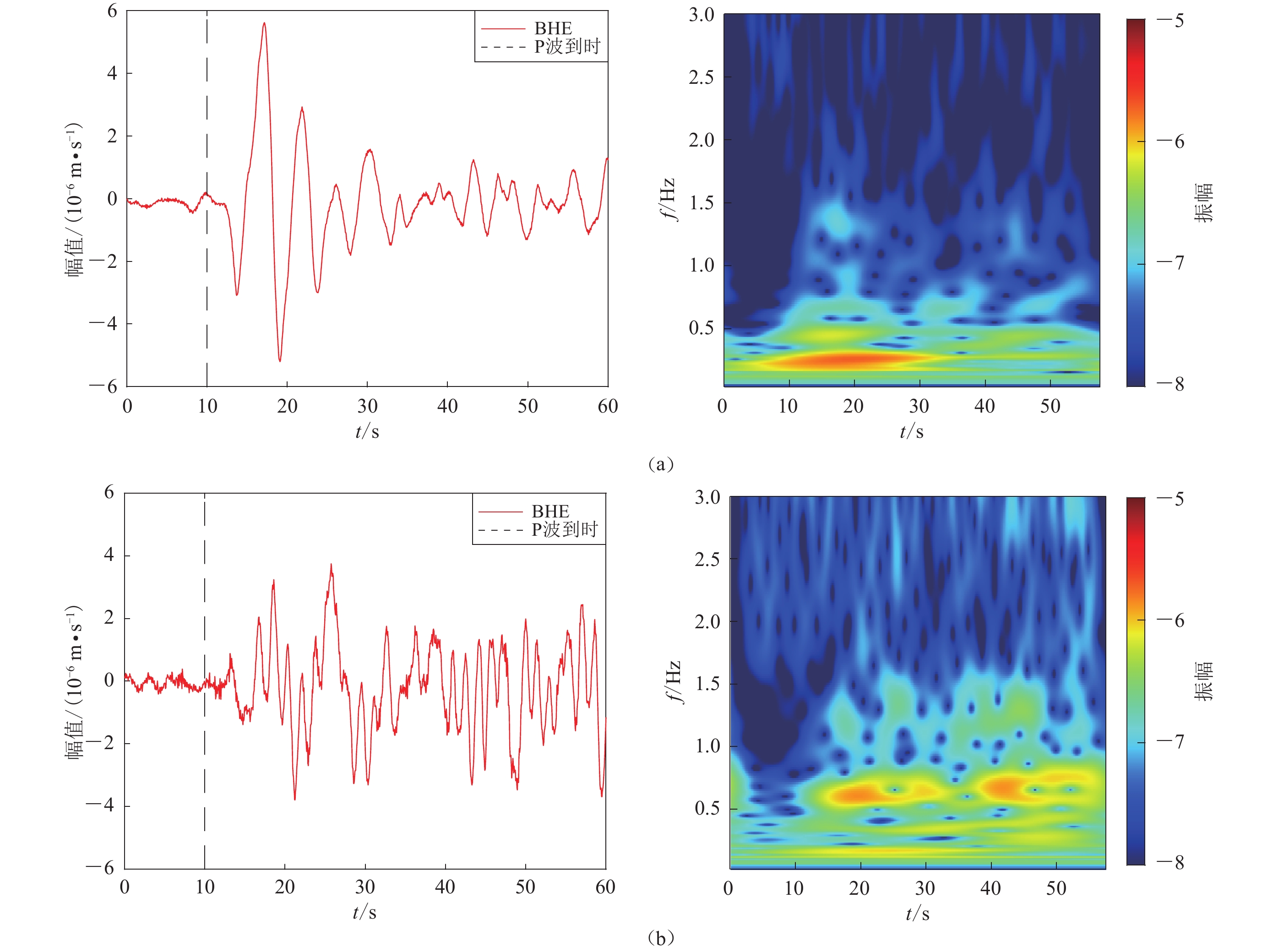
研究震源参数时，选取合适的、有代表性的震例进行对比分析，可以更直观地说明该参数的重要意义。2008年1月9日和2020年7月22日在中国西藏发生了两次大地震，分别是改则地震和尼玛地震。两次地震的矩震级相同，震中仅相距170 km左右，且震源机制非常相似（图5）。经计算，改则地震和尼玛地震的辐射能量分别为1.26×1014 J和0.25×1014 J，能量震级分别为6.47和6.00。
![]()
图 5 2008年1月9日改则MW6.4地震和2020年7月22日尼玛MW6.4地震Figure 5. Gerze MW6.4 earthquake occurred on 9 January 2008 and Niyma MW6.4 earthquake occurred on 22 June 2020 in Xizang，China表 2 西藏改则地震和尼玛地震的地震参数Table 2. Earthquake parameters of the Gerze MW6.4 earthquake and Niyma MW6.4 earthquake发震地点 发震日期 震源深度/km MW Me 辐射能量/（1014J） 能矩比/10−5 震源机制类型 改则 2 008-01-09 13.3 6.4 6.47 1.26 2.5 正断型 尼玛 2 020-07-22 16.8 6.4 6.00 0.25 0.5 正断型 时频分析可以在对数据校正前更好地描述地震记录所提供的信息，图6为牡丹江台（IC.MDJ）记录到的两次事件的波形和S变换（Stockwell et al，1996；Parolai，2009）后的时频分析结果。两次事件震中之间的距离可以忽略不计，地震波从震源到牡丹江台经历的衰减等传播效应基本一致。从图6可以看出，两次地震的能量释放过程存在明显不同：改则地震在P波到时后5—35 s内有一个持续时间较长、强度较大的高频能量脉冲；尼玛地震在P波到时后15—25 s和40—50 s存在两个持续时间较短、强度较小的高频能量脉冲。改则地震的能量释放较为集中且能量较强；而尼玛地震的能量释放相对平缓，强度弱于改则地震。上述差异导致改则地震的能量震级大于尼玛地震，前者的地震辐射能量更是后者的5倍之多。结合地震烈度分布能够更直观地看出地震辐射能量释放的差异，但由于两次事件都发生在人口疏密地区，并没有造成过多伤亡，因此相关地震烈度的研究较少，在此不作过多讨论。综上所述，如果仅考虑震源的静态过程和低频成分，两个事件的S变换的低频幅度是相当的，所以它们的矩震级相同；但从动态过程和高频成分分析，两者的差异十分明显，所以它们的地震辐射能量和能量震级不同。
![]()
图 6 牡丹江台（IC.MDJ）记录到的改则地震（a）和尼玛地震（b）的波形（左）和时频分析（右）图Figure 6. Waveforms （left） recorded by station IC.MDJ of Gerze earthquake （a） and Niyma earthquake （b） and their time-frequency analysis （right）通过对中国青藏高原代表性事件的分析可以发现，地震辐射能量和能量震级等震源参数能够更好地反映震源的高频信息和动态过程，通常被称为动态震源参数。这是地震矩和矩震级等静态震源参数所不具备的，也是工程学上更感兴趣的内容。在其它条件相同的情况下，地震辐射能量的差异是导致地震破坏程度不同的重要原因。关注地震辐射能量特别是高频成分，对地震灾害和风险评估具有重要作用。
3.3 中国青藏高原地区浅源地震的能矩比分布研究
能矩比$ \tilde e $，又称折合能量（reduced energy），是地震辐射能量与地震矩的比值，表征单位地震矩辐射出的地震波能量的大小（Ben-Menahem，Singh，1981；Kanamori，Heaton，2000；Kanamori，Rivera，2006）：
$$ \tilde e ＝ \frac{{{E_{\mathrm{S}}}}}{{{M_0}}} . $$ (6) 能矩比是地震学家长期关注的问题之一。这一无量纲量与地震破裂所产生的应变有关，它直观地反映了震源破裂过程的动力学特征（Newman，Okal，1998；Baltay et al，2014；Okal，2019），因此常被用于研究地震辐射能量规律。
自1973年以来，发生在我国青藏高原的MW≥6.0地震共57例，其中可以直接测定地震辐射能量的地震事件共34例（自1990年起）。虽然我们的程序包含快速震源机制反演功能，但是为了与前人结果保持一致并方便对比分析，我们也采用GCMT的震源机制解。结合GCMT的地震矩结果，得到了中国青藏高原地区浅源地震的平均能矩比为1.9×10−5，是全球浅源地震平均能矩比1.2×10−5 （Choy et al，2006）的1.6倍。中国青藏高原浅源地震的能量释放效率明显高于全球平均水平，在地震矩相同的情况下，中国青藏高原浅源地震释放的能量是全球浅源地震的1.6倍，造成的破坏会更严重、造成的伤亡也会更大。为了更直观地比较地震辐射能量的释放效率，可以将能矩比取对数得到慢度系数Θ （Newman，Okal，1998）。经计算，中国青藏高原浅源地震的平均慢度系数约为−4.72，高于全球浅源地震的平均慢度系数约为−4.59 （Convers，Newman，2011）。
参考GCMT的震源机制解，按照Hauksson （1990）的方法将上述34个地震事件进行简单分类，归为正断层型地震（NF）、逆断层型地震（TF）和走滑断层型地震（SS）三个类型（图7）。其中：正断层型地震9次，平均能矩比为1.21×10−5；逆断层型地震5次，平均能矩比为1.20×10−5；走滑断层型地震20次，平均能矩比为2.35×10−5。上述结果与走滑型地震的能量释放效率高于倾滑型地震的结论一致（Choy，Boatwright，1995）。这是因为应力降具有机制依赖的差异，正断层型地震的视应力介于走滑型地震和逆断层型地震之间，较大的视应力意味着较大的应力降。所以，相比于其它类型的地震，走滑型地震具有更大的视应力降，进而导致此类地震的能量释放略大（Ide，Beroza，2001）；断裂过程中断层表面可能对地震波来说是“不透明的”，地震辐射能量会优先被困在倾斜滑动断层的上盘，导致辐射到远场的能量较少，造成倾滑型地震的能量释放偏小（Brune，1996；Pérez-Campos，Beroza，2001）。
![]()
图 7 中国青藏高原浅源地震的能矩比Figure 7. The energy-moment ratio of shallow earthquakes in Qinghai-Xizang Plateau of China为了探究能矩比的区域特征，对中国青藏高原作了简单划分（图8），分为东部（红色方框）和西部（蓝色方框）两个区域：东部的平均能矩比为2.25×10−5，西部的平均能矩比为1.62×10−5，东部明显高于西部。区域平均能矩比可以体现该地区的能量释放水平，是衡量该地区应力积累情况的间接参数。中国青藏高原东西部能矩比的差异表明，东部地区的应力积累水平高于西部，未来发生高能矩比地震的可能性更大。
![]()
图 8 中国青藏高原东部（红色框）和西部（蓝色框）浅源地震慢度系数（能矩比的对数）的区域分布特征Figure 8. Characteristics of regional distribution of the slowness coefficient （logarithm of energy-moment ratio） in east （red box） and west （blue box） part of Qinghai-Xizang Plateau in China中国青藏高原浅源地震的能矩比存在明显的东西部差异，这一现象的产生是否有相应的地质构造背景？针对这一问题，我们进行了简单地探讨。有研究表明，青藏高原东部和西部存在系统的从地形地貌到壳幔结构的差异（肖龙等，2005）。东部表现为垂向加厚，西部表现为垂向减薄。青藏高原并不是由一个统一完整的地块向东“挤出”，其东部的内部变形非常强烈。从地质构造上讲，青藏高原西部的地壳变形以“厚皮”构造样式以及中新世以来的东西向伸展为特征，“厚皮”构造表现为南北向的大规模基底推覆，东西向的伸展表现为一系列南北向垂直于造山带方向的裂谷与断陷盆地的发育；青藏高原东部（包括三江地区）则表现为强烈的地壳缩短，具备典型的“薄皮”构造样式，表现为大规模的紧闭褶皱作用与走滑断层作用。从断层类型来看，青藏高原西部主要发育以南北向为主的正断层，东部以近东西向的左滑剪切变形构造为主；从地块活动性与孕震规律之间的关系来看，中国大陆绝大部分M7以上地震都发生在活动地块边界的事实表明，地块的运动和地块间的相互作用是地震孕育和发生的直接控制因素。而川滇活动地块就位于青藏高原东部的东南隅，是中国大陆地震活动最强烈的地区之一。川滇活动地块的西南边界为红河断裂带及其北部的拉分构造区，红河断裂是一条右旋走滑断裂；其西北边界是晚第四纪构造活动十分强烈的鲜水河—小江断裂带，该带以左旋走滑为特征。川滇活动地块的边界以走滑剪切为主，所控制的地震也以走滑型为主（张培震，1999），而走滑型地震的能量释放效率要高于逆冲型地震。结合历史资料，发生于青藏高原的地震整体上看震中分布很不均匀，但其西部地震少且震中分布比较均匀，无大地震；有史以来记载的强震、特大震基本都发生在东部（肖龙等，2005）。综上所述，中国青藏高原东西部能矩比的差异分布是有一定地质背景的。区域地震辐射能量可以与地质构造背景相互印证说明地震辐射能量可以一定程度地反映该地区的地质构造，区域地震辐射能量或能矩比规律的研究具有实际意义。
中国青藏高原地区浅源地震的能矩比分布范围为5.03×10−6—4.80×10−5，变化范围达到了一个数量级，这种差异是十分显著的。能矩比变化较大有很多原因。首先，能矩比大小反映的是震源辐射地震波的能力，与断层破裂速度有关。断层破裂速度快，震源就会辐射出大量高频能量；相反地，震源以地震波形式辐射出的能量就会变少。其次，如前文所述，一般认为走滑型地震的能矩比高于倾滑型地震。即使是发震位置相近的两次地震，如果震源机制不同，能矩比差异可能很大。最后，应力积累较强或新鲜破裂的断层上发生的地震的能矩比一般高于应力积累水平较低或未发生新鲜破裂的地震（Choy et al，2006）。发生于同一区域内的地震的能矩比差异反映了地震破裂过程的差异，体现了同一区域内不同地区地震构造的差异性和应力环境变化的复杂性。
4. 讨论与结论
本文使用自主研发的地震辐射能量快速测定软件测定了自1990年至今发生于中国青藏高原的34例MW≥6.0浅源地震的辐射能量和能量震级，根据结果进行了分析和讨论。主要研究结论如下：
1） 测定了中国青藏高原34例浅源地震的地震辐射能量ES和能量震级Me等动态震源参数，将测定结果与IRIS发布的结果相比较发现，本文的测定结果与IRIS发布的能量震级结果相差仅在±0.05之间，说明本文使用的测定方法较为科学，测定结果稳定、可靠。不同类型的震级标度之间的对比表明，一般情况下面波震级MS与能量震级Me、矩震级MW与能量震级Me并不相等。相比于面波震级仅为特定频率下测量的震级标度，能量震级是在跨震源谱的所有频段的积分，能更好地描述地震的“大小”。为了更全面地评估地震动效应，需要综合考虑震源的静态特征和动态特征。因此，联合测定面波震级、矩震级和能量震级可以更好地为防震减灾提供参考。
2） 改则地震和尼玛地震的能量震级分别为6.47和6.00，地震辐射能量分别为1.26×1014 J和0.25×1014 J。通过代表性震例的对比分析可知，即使矩震级相同、震源位置基本一致且震源机制相似的两次地震，它们的地震辐射能量和能量震级也可以相差很大。时频分析结果表明，震源动态过程和高频成分的不同决定了动态震源参数的差异。相比于地震矩和矩震级，地震辐射能量和能量震级等地震参数能更好地反映震源的动态过程并分析地震的潜在破坏性，测定地震辐射能量和能量震级可以更全面地描述地震事件，弥补地震矩和矩震级的不足。
3） 本文测定得到中国青藏高原地区浅源地震的平均能矩比为1.9×10−5，是全球浅源地震平均能矩比1.2×10−5的1.6倍。以上数字表明，中国青藏高原地区浅源地震的能量释放水平高于全球平均水平，即同等情况下释放的能量更大，造成的破坏也会更严重。
4） 通过测定中国青藏高原浅源地震的地震辐射能量并计算其能矩比，得到中国青藏高原东部的平均能矩比为2.25×10−5，西部的平均能矩比为1.62×10−5，东部明显高于西部。说明中国青藏高原地区浅源地震能矩比的整体分布存在区域差异，也反映了东部的应力积累水平高于西部。同时，通过对产生这种区域差异的原因进行探究我们发现：中国青藏高原东西部能矩比差异可能与地质构造背景有关，地震辐射能量可以反映该地区的地质构造状态。除能矩比分布的区域特征外，同一区域内地震能矩比也存在差别，这一现象表明不同断层上发生地震的能量释放过程存在差异。虽然中国青藏高原地区浅源地震的能矩比分布的区域特征具有一定的构造背景，然而本文仍未建立两者之间的确切关系。如果能够解决这一问题，将极大地帮助人们了解地震的致灾机理。
本文使用的数据来自美国地震学联合研究会（IRIS）数据中心，部分图片由GMT （Wessel，Smith，1991）绘制，震源机制解目录来自全球矩心矩张量项目（GCMT），作者在此一并表示感谢。
-
![]()
图 1 中国青藏高原MW≥6.0浅源地震分布
Figure 1. Earthquakes with MW≥6.0 occurred in Qinghai-Xizang Plateau in China
![]()
图 2 本文测定的地震辐射能量（a）和能量震级（b）与IRIS结果的对比
Figure 2. Comparison of radiated seismic energy （a） and Me （b） between IRIS and this paper
![]()
图 5 2008年1月9日改则MW6.4地震和2020年7月22日尼玛MW6.4地震
Figure 5. Gerze MW6.4 earthquake occurred on 9 January 2008 and Niyma MW6.4 earthquake occurred on 22 June 2020 in Xizang，China
![]()
图 6 牡丹江台（IC.MDJ）记录到的改则地震（a）和尼玛地震（b）的波形（左）和时频分析（右）图
Figure 6. Waveforms （left） recorded by station IC.MDJ of Gerze earthquake （a） and Niyma earthquake （b） and their time-frequency analysis （right）
![]()
图 7 中国青藏高原浅源地震的能矩比
Figure 7. The energy-moment ratio of shallow earthquakes in Qinghai-Xizang Plateau of China
![]()
图 8 中国青藏高原东部（红色框）和西部（蓝色框）浅源地震慢度系数（能矩比的对数）的区域分布特征
Figure 8. Characteristics of regional distribution of the slowness coefficient （logarithm of energy-moment ratio） in east （red box） and west （blue box） part of Qinghai-Xizang Plateau in China
表 1 中国青藏高原浅源地震的震源参数
Table 1 Source parameters of shallow earthquakes in Qinghai-Xizang Plateau in China
发震日期
a-mo-d震中位置 震源
深度
/kmM0
/（1018 N·m）MW MS ES
/（1013J）Me I Me 震源机制
类型参考位置 东经/° 北纬/° 1 990-04-26 100.28 36.02 10.0 5.61 6.4 6.9 26.7 6.65 6.68 走滑型 青海共和 1 992-07-30 90.18 29.57 31.4 1.79 6.1 5.8 1.93 5.92 5.92 正断型 西藏尼木 1 993-10-02 88.66 38.17 14.1 1.64 6.1 6.3 7.76 6.28 6.33 走滑型 新疆若羌 1 996-02-03 100.29 27.29 10.0 9.94 6.6 6.5 23.2 6.62 6.64 正断型 云南丽江 1 997-04-11 96.95 39.56 20.0 2.06 6.1 6.1 2.96 6.09 6.05 走滑型 新疆伽师 1 997-11-08 87.37 35.12 38.1 223 7.5 7.9 150 7.22 7.18 走滑型 西藏尼玛 1 998-08-27 77.34 39.58 33.0 3.89 6.3 6.4 9.61 6.43 6.39 走滑型 新疆伽师 2 000-09-12 99.37 35.37 12.0 1.76 6.1 6.3 1.92 5.95 5.92 走滑型 青海兴海 2 001-11-14 90.59 35.93 11.0 590 7.8 8.0 582 7.60 7.58 走滑型 昆仑山口 2 003-02-24 77.21 39.52 26.2 3.74 6.3 6.3 2.14 6.00 5.95 逆断型 巴楚—伽师 2 003-04-17 96.51 37.52 15.0 4.12 6.3 6.3 6.55 6.26 6.28 逆断型 青海德令哈 2 004-03-27 89.18 33.99 9.0 1.11 6.0 5.8 1.41 5.84 5.83 正断型 西藏班戈 2 004-07-11 83.67 30.72 8.1 2.36 6.2 6.2 2.14 6.00 5.95 正断型 西藏仲巴 2 005-04-07 83.66 30.52 14.7 3.35 6.3 6.1 3.23 6.07 6.07 正断型 西藏仲巴 2 007-05-05 82.03 34.27 14.2 1.54 6.1 6.0 3.27 6.03 6.08 走滑型 日土—改则 2 008-01-09 85.26 32.4 27.7 5.02 6.4 6.4 12.6 6.42 6.47 正断型 西藏改则 2 008-03-20 81.51 35.55 10.0 54.3 7.1 7.3 39.5 6.82 6.80 正断型 新疆于田 2 008-05-12 103.37 31.06 7.6 897 7.9 8.1 2910 8.06 8.04 逆冲型 四川汶川 2 008-05-12 103.63 31.24 11.5 1.65 6.1 6.1 3.55 6.15 6.10 走滑型 四川汶川 2 008-10-06 90.38 29.84 6.4 3.65 6.3 6.3 3.70 6.11 6.11 走滑型 西藏当雄 2 008-11-10 95.89 37.62 0.1 4.06 6.3 6.4 10.1 6.38 6.40 走滑型 青海海西 2 009-08-28 95.76 37.67 12.1 3.04 6.3 6.2 2.62 6.05 6.01 逆断型 青海海西 2 010-04-13 96.75 33.19 13.8 25.3 6.9 7.0 46.8 6.83 6.85 走滑型 青海玉树 2 012-08-12 82.54 35.65 14.0 2.55 6.2 6.3 2.18 6.00 5.96 走滑型 新疆于田 2 013-04-20 103.02 30.27 18.0 10.2 6.6 6.8 25.3 6.70 6.67 逆断型 四川雅安 2 014-02-12 82.58 35.88 4.1 28.7 6.9 6.9 113 7.07 7.10 走滑型 新疆于田 2 014-08-03 103.43 27.25 10.0 2.12 6.2 6.2 10.2 6.39 6.41 走滑型 云南鲁甸 2 015-07-03 78.12 37.47 19.0 5.33 6.4 6.4 3.10 6.11 6.06 逆断型 新疆皮山 2 016-10-17 94.87 32.91 32.1 1.20 6.0 5.9 1.81 5.88 5.90 走滑型 青海杂多 2 016-11-25 74.02 39.23 17.0 11.3 6.6 6.6 51.6 6.90 6.87 走滑型 新疆阿克陶 2 017-08-08 103.86 33.19 9.0 6.98 6.5 6.5 10.8 6.40 6.42 走滑型 四川九寨沟 2 020-06-25 82.42 35.59 10.0 3.23 6.3 6.3 1.81 5.91 5.91 正断型 新疆于田 2 020-07-22 86.87 33.15 10.0 5.04 6.4 6.3 2.54 6.04 6.00 正断型 西藏尼玛 2 021-05-21 98.24 34.59 10.0 166 7.4 7.3 137 7.20 7.16 走滑型 青海玛多 注：经纬度信息及MeI来自IRIS；M0，MW和MS来自GCMT；ES和Me为本文测定的地震辐射能量和能量震级。 
下载: 导出CSV
表 2 西藏改则地震和尼玛地震的地震参数
Table 2 Earthquake parameters of the Gerze MW6.4 earthquake and Niyma MW6.4 earthquake
发震地点 发震日期 震源深度/km MW Me 辐射能量/（1014J） 能矩比/10−5 震源机制类型 改则 2 008-01-09 13.3 6.4 6.47 1.26 2.5 正断型 尼玛 2 020-07-22 16.8 6.4 6.00 0.25 0.5 正断型
下载: 导出CSV
-
陈运泰,顾浩鼎. 1990. 震源理论基础(上册)[M]. 北京:中国地震局地球物理研究所:1−190. Chen Y T,Gu H D. 1990. The Theoretical Basis of Earthquake Source (Volume I)[M]. Beijing:Institute of Geophysics,China Earthquake Administration:1−190 (in Chinese).
孔韩东,刘瑞丰,边银菊,李赞,王子博,胡岩松. 2022. 地震辐射能量测定方法研究及其在汶川8.0级地震中的应用[J]. 地球物理学报,65(12):4775–4788. doi: 10.6038/cjg2022Q0169 Kong H D,Liu R F,Bian Y J,Li Z,Wang Z B,Hu Y S. 2022. Research on the method to determine the seismic radiated energy and its application in Wenchuan M8.0 earthquake[J]. Chinese Journal of Geophysics,65(12):4775–4788 (in Chinese).
王子博,刘瑞丰,孙丽,李赞,孔韩东. 2021. 2021年云南漾濞MS6.4地震辐射能量的快速测定[J]. 地震地质,43(4):908–919. doi: 10.3969/j.issn.0253-4967.2021.04.011 Wang Z B,Liu R F,Sun L,Li Z,Kong H D. 2021. The rapid determination of radiated seismic energy of MS6.4 Yangbi earthquake[J]. Seismology and Geology,43(4):908–919 (in Chinese).
肖龙,王春增,Pirajno F. 2005. 青藏高原东西向地质构造差异及其成因探讨[C]//青藏高原地质过程与环境灾害效应学术讨论会. 北京:中国地质学会:221−227. Xiao L,Wang C Z,Pirajno F. 2005. Geological tectonic differences and their causes in the east-west direction of the Qinghai-Xizang Plateau[C]//In Proceedings of the Academic Symposium on Geological Processes and Environmental Disaster Effects in the Qinghai-Xizang Plateau. Beijing:Geological Society of China:221−227 (in Chinese).
张培震. 1999. 中国大陆岩石圈最新构造变动与地震灾害[J]. 第四纪研究,(5):404–413. doi: 10.3321/j.issn:1001-7410.1999.05.003 Zhang P Z. 1999. Late Quaternary tectonic deformation and earthquake hazard in continental China[J]. Quaternary Sciences,(5):404–413 (in Chinese).
Allmann B P,Shearer P M. 2009. Global variations of stress drop for moderate to large earthquakes[J]. J Geophys Res:Solid Earth,114(B1):B01310.
Baltay A S,Beroza G C,Ide S. 2014. Radiated energy of great earthquakes from teleseismic empirical Green’s function deconvolution[J]. Pure Appl Geophys,171(10):2841–2862. doi: 10.1007/s00024-014-0804-0
Ben-Menahem A,Singh S J. 1981. Seismic Waves and Sources[M]. New York:Springer:622−767.
Boatwright J,Choy G L. 1986. Teleseismic estimates of the energy radiated by shallow earthquakes[J]. J Geophys Res:Solid Earth,91(B2):2095–2112. doi: 10.1029/JB091iB02p02095
Boatwright J,Choy G L,Seekins L C. 2002. Regional estimates of radiated seismic energy[J]. Bull Seismol Soc Am,92(4):1241–1255. doi: 10.1785/0120000932
Boatwright J,Seekins L. 2011. Regional spectral analysis of three moderate earthquakes in northeastern North America[J]. Bull Seismol Soc Am,101(4):1769–1782. doi: 10.1785/0120100225
Bormann P,Baumbach M,Bock G,Grosser H,Choy G L,Boatwright J. 2002. Seismic sources and source parameters[M]//New Manual of Seismological Observatory Practice. Potsdam:Deutsches GeoForschungsZentrum:1−94.
Brune J N. 1996. Particle motions in a physical model of shallow angle thrust faulting[J]. Proc Indian Acad Sci:Earth Planet Sci,105(2):197–206. doi: 10.1007/BF02876014
Choy G L,Boatwright J L. 1995. Global patterns of radiated seismic energy and apparent stress[J]. J Geophys Res:Solid Earth,100(B9):18205–18228. doi: 10.1029/95JB01969
Choy G L,Kirby S H. 2004. Apparent stress,fault maturity and seismic hazard for normal-fault earthquakes at subduction zones[J]. Geophys J Int,159(3):991–1012. doi: 10.1111/j.1365-246X.2004.02449.x
Choy G L,McGarr A,Kirby S H,Boatwright J. 2006. An overview of the global variability in radiated energy and apparent stress[M]//Earthquakes:Radiated Energy and the Physics of Faulting. Washington,DC:American Geophysical Union:43−57.
Choy G L,Boatwright J. 2009. Differential energy radiation from two earthquakes in Japan with identical MW:The Kyushu 1996 and Tottori 2000 earthquakes[J]. Bull Seismol Soc Am,99(3):1815–1826. doi: 10.1785/0120080078
Choy G L. 2012. Stress conditions inferable from modern magnitudes:Development of a model of fault maturity[M]//New Manual of Seismological Observatory Practice 2 (NMSOP-2). Potsdam:Deutsches GeoForschungsZentrum:1−10.
Convers J A,Newman A V. 2011. Global evaluation of large earthquake energy from 1997 through mid-2010[J]. J Geophys Res:Solid Earth,116(B8):B08304.
Di Giacomo D,Grosser H,Parolai S,Bormann P,Wang R J. 2008. Rapid determination of Me for strong to great shallow earthquakes[J]. Geophys Res Lett,35(10):L10308.
Di Giacomo D. 2010. Determination of the Energy Magnitude Me:Application to Rapid Response Purposes and Insights to Regional/Local Variabilities[D]. Potsdam:Universität Potsdam:1−132.
Di Giacomo D,Parolai S,Bormann P,Grosser H,Saul J,Wang R J,Zschau J. 2010. Suitability of rapid energy magnitude determinations for emergency response purposes[J]. Geophys J Int,180(1):361–374. doi: 10.1111/j.1365-246X.2009.04416.x
Gutenberg B,Richter C F. 1956. Earthquake magnitude,intensity,energy,and acceleration[J]. Bull Seismol Soc Am,46(2):105–145. doi: 10.1785/BSSA0460020105
Hanks T C,Kanamori H. 1979. A moment magnitude scale[J]. J Geophys Res:Solid Earth,84(B5):2348–2350. doi: 10.1029/JB084iB05p02348
Haskell N A. 1964. Total energy and energy spectral density of elastic wave radiation from propagating faults[J]. Bull Seismol Soc Am,54(6A):1811–1841. doi: 10.1785/BSSA05406A1811
Hauksson E. 1990. Earthquakes,faulting,and stress in the Los Angeles Basin[J]. J Geophys Res:Solid Earth,95(B10):15365–15394. doi: 10.1029/JB095iB10p15365
Husseini M I. 1977. Energy balance for motion along a fault[J]. Geophys J Int,49(3):699–714. doi: 10.1111/j.1365-246X.1977.tb01313.x
Ide S,Beroza G C. 2001. Does apparent stress vary with earthquake size?[J]. Geophys Res Lett,28(17):3349–3352. doi: 10.1029/2001GL013106
Kanamori H,Mori J,Hauksson E,Heaton T H,Hutton L K,Jones L M. 1993. Determination of earthquake energy release and ML using Terrascope[J]. Bull Seismol Soc Am,83(2):330–346.
Kanamori H,Heaton T H. 2000. Microscopic and macroscopic physics of earthquakes[M]//Geocomplexity and the Physics of Earthquakes. Washington,DC:American Geophysical Union:147−163.
Kanamori H,Rivera L. 2006. Energy partitioning during an earthquake[M]//Earthquakes:Radiated Energy and the Physics of Faulting. Washington,DC:American Geophysical Union:3−13.
Kanamori H,Ross Z E,Rivera L. 2020. Estimation of radiated energy using the KiK-net downhole records-old method for modern data[J]. Geophys J Int,221(2):1029–1042. doi: 10.1093/gji/ggaa040
Lay T,Wallace T C. 1995. Modern Global Seismology[M]. San Diego:Academic Press:1−521.
Mayeda K,Walter W R. 1996. Moment,energy,stress drop,and source spectra of western United States earthquakes from regional coda envelopes[J]. J Geophys Res:Solid Earth,101(B5):11195–11208. doi: 10.1029/96JB00112
Mayeda K,Hofstetter A,O’Boyle J L,Walter W R. 2003. Stable and transportable regional magnitudes based on coda-derived moment-rate spectra[J]. Bull Seismol Soc Am,93(1):224–239. doi: 10.1785/0120020020
Montagner J P,Kennett B L N. 1996. How to reconcile body-wave and normal-mode reference Earth models[J]. Geophys J Int,125(1):229–248. doi: 10.1111/j.1365-246X.1996.tb06548.x
Morasca P,Mayeda K,Malagnini L,Walter W R. 2005. Coda-derived source spectra,moment magnitudes and energy-moment scaling in the western Alps[J]. Geophys J Int,160(1):263–275.
Newman A V,Okal E A. 1998. Teleseismic estimates of radiated seismic energy:The E/M0 discriminant for tsunami earthquakes[J]. J Geophys Res:Solid Earth,103(B11):26885–26898. doi: 10.1029/98JB02236
Okal E A. 2019. Energy and magnitude:A historical perspective[J]. Pure Appl Geophys,176(9):3815–3849. doi: 10.1007/s00024-018-1994-7
Parolai S. 2009. Denoising of seismograms using the S transform[J]. Bull Seismol Soc Am,99(1):226–234. doi: 10.1785/0120080001
Pérez-Campos X,Beroza G C. 2001. An apparent mechanism dependence of radiated seismic energy[J]. J Geophys Res:Solid Earth,106(B6):11127–11136. doi: 10.1029/2000JB900455
Rudnicki J W,Freund L B. 1981. On energy radiation from seismic sources[J]. Bull Seismol Soc Am,71(3):583–595.
Singh S K,Ordaz M. 1994. Seismic energy release in Mexican subduction zone earthquake[J]. Bull Seismol Soc Am,84(5):1533–1550.
Stockwell R G,Mansinha L,Lowe R P. 1996. Localization of the complex spectrum:The S transform[J]. IEEE Trans Signal Process,44(4):998–1001. doi: 10.1109/78.492555
Tajima R,Tajima F. 2007. Seismic scaling relations and aftershock activity from the sequences of the 2004 mid Niigata and the 2005 west off Fukuoka earthquakes (MW6.6) in Japan[J]. J Geophys Res:Solid Earth,112(B10):B10302.
Vassiliou M S,Kanamori H. 1982. The energy release in earthquakes[J]. Bull Seismol Soc Am,72(2):371–381.
Venkataraman A,Kanamori H. 2004a. Effect of directivity on estimates of radiated seismic energy[J]. J Geophys Res:Solid Earth,109(B4):B04301.
Venkataraman A,Kanamori H. 2004b. Observational constraints on the fracture energy of subduction zone earthquakes[J]. J Geophys Res:Solid Earth,109(B5):B05302.
Wessel P,Smith W. 1991. Free software helps map and display data[J]. Eos Trans AGU,72:441 doi: 10.1002/2015JB012426
计量
- 文章访问数: 170
- HTML全文浏览量: 40
- PDF下载量: 48
