Teleseismic P-wave data reconstruction based on compressive sensing theory
-
摘要:
本文将基于压缩感知理论的地震观测数据重建方法用于天然远震事件的P波到时处理之中，基于曲波（curvelet）变换，建立基于L1范数的正则化反演模型，并采用迭代收缩阈值算法（ISTA）求解该模型。针对在内蒙古布设的流动地震台阵记录到的远震波形数据，对其进行稀疏采样，采用稀疏反演重建方法对欠采样数据进行重建，并拾取重建数据的P波到时，之后开展远震P波层析成像进行验证。研究结果表明，远震天然地震观测数据在曲波变换中表现出稀疏性，可利用压缩感知方法实现远震P波数据的完备化处理。基于内蒙古流动地震台阵数据三维P波成像也表明，基于压缩感知的数据重建技术可以提高地震层析成像的分辨率，且压缩感知采集技术在天然地震研究中具有潜在的应用价值。
Abstract:The non-uniformity and incompleteness of seismic data in space have long been one of the significant challenges affecting seismic imaging. The factors that cause the non-uniform spatial distribution of seismic data are primarily twofold: Firstly, the non-uniform distribution of earthquakes, which are the sources of seismic waves; Secondly, the non-uniform distribution of seismic stations used to record these waves. In areas where stations are difficult to built, such as mountainous regions and offshore locations, uniform array deployment becomes impractical. These factors lead to the acquisition of non-uniform and incomplete data, thereby reducing the resolution and accuracy of the imaging results.
The core principle of compressed sensing theory is to exploit the sparse nature of the signal and then employ a non-linear reconstruction algorithm to recover the original signal. Since seismic wavefields exhibit continuity, then missing or irregularly sampled seismic data can potentially be recovered through compressed sensing techniques. In the time domain, seismic observation data usually contain rich frequency information. However, due to the filtering effects of subsurface layers, the bandwidth of the actual recorded seismic data is limited, and the data exhibit sparsity in the frequency domain. Based on this characteristic, under limited acquisition conditions, the reconstruction of missing seismic data utilizing compressed sensing theory can, to some extent, mitigate the problem of insufficient seismic data coverage.
In oil and gas seismic exploration, data reconstruction methods based on compressed sensing theory have been widely applied to address the issue of insufficient sampling. However, relevant discussions are not yet common in the acquisition and processing of natural earthquake data. In fact, due to environmental and site constraints, the acquisition of natural earthquake data also suffers missing and irregular sampling issues. Moreover, owing to the irregular distribution of acquisition stations, the reconstruction of natural earthquake data encounters greater challenges. Natural earthquake waveforms are more complex, and proposing a reliable scheme for reconstructing natural earthquake data under the condition of irregularly distributed acquisition stations is a relatively difficult problem.
For artificial seismic exploration data reconstruction, the trace spacing is small, and the waveforms of adjacent traces exhibit good consistency. In Chinese continental natural earthquake observation stations, the minimum station spacing is less than 30 km, and the teleseismic waveforms recorded at different stations also exhibit certain similarities. This study commences with natural teleseismic observation data, draws upon the experience of artificial seismic data reconstruction, and attempts to conduct research on the reconstruction of teleseismic data. Relevant experimental verifications have been carried out.
To verify the reconstruction effect of the algorithm, we first use the reflectivity method to calculate the theoretical seismogram, simulating the teleseismic P-wave data recorded by the Inner Mongolia movable array. Thirty-six seismic stations receive the data, with a sampling interval of 2 ms and 5501 sampling points. The simulated seismic data are obtained through calculation of seismic travel time, and the missing teleseismic P-wave data are recovered, verifying the effectiveness of the method. Compared with the original record, the reconstructed seismic record signals can restore the waveform relatively well; the reconstructed result is generally consistent with the original record. In terms of amplitude, the reconstructed result is significantly smaller, and the frequency is also higher, which shows that the reconstruction method has the effect of suppressing random noise. Simultaneously, there are certain differences in the waveforms across different stations, and the analysis suggests that the number of iterations for certain station data is insufficient, or there are discrepancies in parameter adjustments.
We applied the seismic data reconstruction method that based on compressed sensing to process P-wave arrival times of teleseismic events. Firstly, the curvelet transform is utilized as a sparse transform, and a regularized inversion model based on the L1 norm is established. The iterative shrinkage-thresholding algorithm （ISTA） is employed to solve this model. Subsequently, the compressed sensing theory is applied to the reconstruction of teleseismic data observed by the portable seismic array in the Inner Mongolia region. On this basis, data reconstruction is performed on the acquired real earthquake data, and the reconstructed P-wave arrival time data are picked to verify the effectiveness of the method through teleseismic tomography.
The practice of natural earthquake data reconstruction demonstrates that natural earthquake data exhibit a sparse representation in the curvelet transform domain. Based on the seismic data itself, when seismic data are missing or the natural earthquake observation data are incomplete, the compressed sensing theory can be employed to reconstruct the seismic data. Concurrently, this method can be utilized to reconstruct data with poor signal-to-noise ratio and obtain high signal-to-noise ratio seismic data. In this study, the fast marching teleseismic tomography （FMTT） method is used to invert the velocity structure from the original data, sampled data, and reconstructed seismic data, respectively. The results indicate that when data are missing, the calculated tomographic velocity structure deviates significantly from that calculated with complete data. The relative error between the tomographic result obtained from the reconstructed data and that from the complete data is within 0.02%. The vertical cross-section shows that the tomographic results obtained from the original data and reconstructed data exhibit highly similar travel time residuals, and the spatial positions and shapes of the main high and low velocity anomaly zones are highly consistent. This signifies that the compressed sensing based theory reconstruction method can recover the imaging results from the sampled data. The practice of three-dimensional P-wave imaging proves that the data reconstruction technique based on compressed sensing theory can improve the resolution of seismic tomography. The results also demonstrate the potential application value of compressed sensing acquisition technology in natural earthquake data, which can provide and broaden the research ideas for exploring new array observation methods and data acquisition strategies for natural earthquakes.
-
Keywords:
- compressive sensing /
- curvelet transform /
- teleseismic P-wave /
- seismic reconstruction /
- L1 norm
-
引言
地震体波走时反演通过计算大量交叉的地震波射线路径来获取射线所经过介质的速度信息，可有效地降低反演的非唯一性（Rawlinson et al，2010）。然而，受到地震台站分布稀疏的限制，地震波射线分布具有明显的不均匀性，从而影响了成像的分辨率和精度（赵杨，2018）。地震台站的个数和分布相对于要求解的地下结构的参数而言远远不够，因此，层析成像本质上是一个求解欠定反问题的过程，获得的解具有多解性，为此，科研人员经常采用加密地震台站、减小解空间范围等方法来克服该问题。
压缩感知理论的核心思想是先挖掘信号的稀疏特性，再利用非线性重建算法恢复原始信号（Donoho，2006；付明柏，2013；孔德辉，2017；郑雪辰，2019）。由于地震波场具有连续性，缺失或不规则的地震数据可以通过压缩感知理论得到恢复（Candès et al，2006a）。时间域的地震观测数据的频率信息通常较为丰富，然而经过地层的滤波作用，实际采集到的地震数据的频谱宽度会受到限制（孔德辉，2017），使得地震数据在频率域则表现出稀疏性（Herrmann，Hennenfent，2008；Zhou et al，2015）。基于上述特性，在采集条件有限的情况下，根据压缩感知理论，重建缺失的地震数据可在一定程度上弥补地震数据不足的问题（Zhang et al，2007；Wang et al，2016；孔德辉，2017）。
压缩感知理论数据重建方法已很好地应用于油气地震勘探（Herrmann，Hennenfent，2008；曹静杰等，2012，2017，2020；白兰淑等，2014；Cao et al，2015；Bai et al，2020），而在天然地震采集和数据处理中的相关讨论却不多见。实际上，由于受环境和场地限制，天然地震数据采集同样存在缺失和不规则的问题，并且由于采集台站分布的不规则，天然地震的数据重建更加富有挑战性。Ismael等（2012）在地震台站布设空区进行地震数据模拟重建，并计算震源机制解，结果表明由该重建数据计算得到的震源机制解结果与基于周边台站实际采集数据计算的震源机制解结果吻合。白兰淑等（2022）采用压缩感知方法获得了高分辨率接收函数叠加成像。压缩感知方法作为一种新兴的采样及信号恢复方法，能很好地从非完备和非精确的采集数据中恢复出稳定的采样信号（Candès et al，2006b），且基于压缩感知理论重建人工地震数据已经取得了一些成果，但是对于天然地震波形的重建更加复杂，如何在采集台站不规则的情况下提出可靠的重建天然地震数据的方案是科研人员面临的比较困难的问题。人工地震勘探数据重建道间距小，相邻道所记录的波形具有良好的一致性，我国大陆天然地震观测台站最小间距不足30 km，不同台站记录的远震波形同样具有一定的相似性。
本研究从天然远震观测数据着手，借鉴人工地震数据重建经验，尝试开展远震地震数据重建的研究，并进行相关的试验验证。本文拟基于压缩感知理论，建立基于L1范数的正则化反演模型，采用迭代收缩阈值法进行求解，并开展远震P波层析成像以验证该数据重建方法的有效性，最后将该方法应用于内蒙古地区观测到的部分地震台阵数据，以期对提高现有地震台网的成像分辨率提供技术支撑。
1. 基于压缩感知理论的天然地震数据重建方法
2006年，压缩感知采样定理首次被证明并开始应用（Donoho，2006；Candès et al，2006b），当采样信号满足稀疏性条件时，可采用某个线性投影的方式来对信号进行压缩，即
$$ y ＝ {\boldsymbol{\varPhi}} x ＝ {\boldsymbol{\varPhi}} {{\varPsi}} \alpha {\text{，}} $$ (1) 式中，$ y $为观测信号，$ {{\boldsymbol{\varPhi}} } $为测量矩阵，$ x $为原始信号，$ \varPsi $为变换基，$ \alpha $则用来表示信号的稀疏。
地震信号采集过程可以表示为
$$ {\boldsymbol{R}}\boldsymbol{x}{\text{＋}} \mathrm{\varepsilon }＝d \text{，} $$ (2) 式中：$ {\boldsymbol{x}} $为完整的地震数据（大小为M×N，M为地震道个数，N为地震记录长度）；$ \boldsymbol{R} $为采样矩阵，大小为M×N （M＜N），这里表示将x中的部分记录道置零；$ \varepsilon $为长度为N的可加性噪声；$ d $为长度为N的采样数据。根据地震数据的稀疏性，可令$ s {\text{＝}} \psi $x，其中，$ \psi $是一个稀疏变换算子，s是稀疏变换域系数。由于共轭转置也是其逆，即$ {{\psi }^{\mathrm{*}} {\text{＝}} \psi }^{-1} $，则式（2）变为
$$ {{{\boldsymbol{R}}}\psi }^{\mathrm{*}}s {\text{＋}} \varepsilon {\text{＝}} d \text{，} $$ (3) 由式（3）可知，由采样数据d求解稀疏解s是一个欠定问题，可通过如下约束优化获得稀疏解s：
$$ \mathrm{m}\mathrm{i}\mathrm{n}{\left\| {{{{\boldsymbol{R}}}}{\psi }^{\mathrm{*}}s{\text{－}}d} \right\|}_{2}^{2} {\text{＋}} {\lambda \left\| {s} \right\|}_{1} \text{，} $$ (4) 式中$ \lambda $为平衡残差的L2范数和解的L1范数的正则参数。
式（4）是一个凸优化问题，可以通过梯度类算法进行求解。在众多梯度类算法中，迭代收缩阈值算法（iterative shrinkage thresholding algorithm，缩写为ISTA）是一种非常稳定的算法，该算法在每次迭代中使用一个收缩软阈值得到更新的$ s $，具体的迭代方法为（Daubechies et al，2004）：
$$ {s}_{{n}+1} {\text{＝}} \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\left\{{{s}}_{{n}} {\text{＋}} \frac{1}{\mathrm{\alpha }}\mathrm{\psi } （ {\mathrm{\psi }}^{\mathrm{*}}{{s}}_{{n}}{\text{－}}{d} ） {\text{，} }\frac{\mathrm{\lambda }}{2\mathrm{\alpha }}\right\} \text{，} $$ (5) 式中：n为迭代次数；$ \alpha $为步长；$ \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t} （ {y} {\text{，}} {t} ） $为定义的软阈值函数，当输入$ y $为复数时，令$ y {\text{＝}} {{\textit{z}}}{\mathrm{e}}^{-\mathrm{i}\mathrm{\omega }} $，z为y的模，则有
$$ \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t} （ y {\text{，} }t ） =\left\{\begin{array}{l} （ {\textit{z}}{\text{－}}t ） {\mathrm{e}}^{-\mathrm{i}\omega }\qquad {\textit{z}} {\text{≥}} t，\\ 0 \qquad \qquad\quad \,\,\,\,\,{\textit{z}} ＜ t，\end{array}\right. $$ (6) 则式（4）的解为$ {x}_{n} {\text{＝}} {\psi }^{\mathrm{*}}{s}_{n} $。
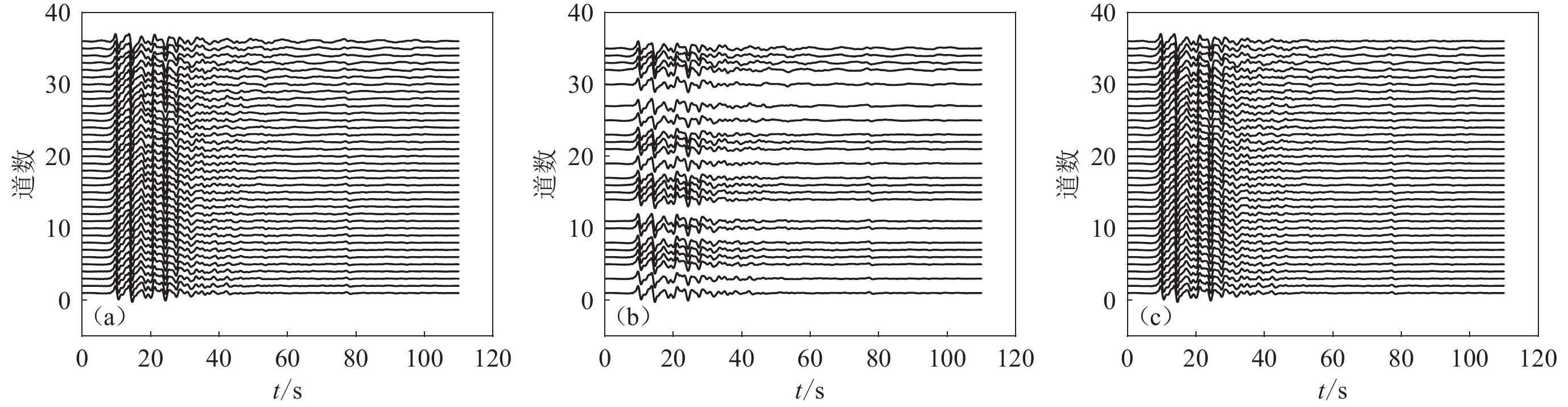
为了检验上述算法的重建效果，本文首先采用反透射系数法（Wang，1999）计算理论地震图以模拟天然地震P波数据，模拟内蒙古流动台阵记录的2012年11月13日20:42:14.620的M6.3地震，震中位置为（57.79°N，142.85°W），震源深度为9 km。台阵共布设36个地震台站用以接收数据，采样间隔为2 ms，采样点为5 501个。经计算得到了模拟地震数据（图1a），随机采样数据如图1b所示，重建数据如图1c所示。对比图1a与图1c，缺失的天然地震P波数据得以恢复，验证了该方法的有效性。
![]()
图 1 模拟天然地震数据重建（a） 原始数据；（b） 采样数据；（c） 重建数据Figure 1. Reconstruction of simulated natural earthquake data（a） Simulation data；（b） Sampling data；（c） Reconstruction data从单道地震原始记录波形（图2）可以看出，经过重建后的地震记录相比原始记录，信号形态能够被较好地恢复出来。从图2每幅图的后半部来看，图2a和图2b重建的结果与原始记录基本吻合；但从图2c和图2d来看，重建结果的幅值明显变小，频率也增高，说明重建方法具有压制随机噪声的效果，特别是图2d中的台站波形与其它台站波形存在一定的差异，其原因是对某一台站数据迭代次数不够，或者参数调节存在差异。
![]()
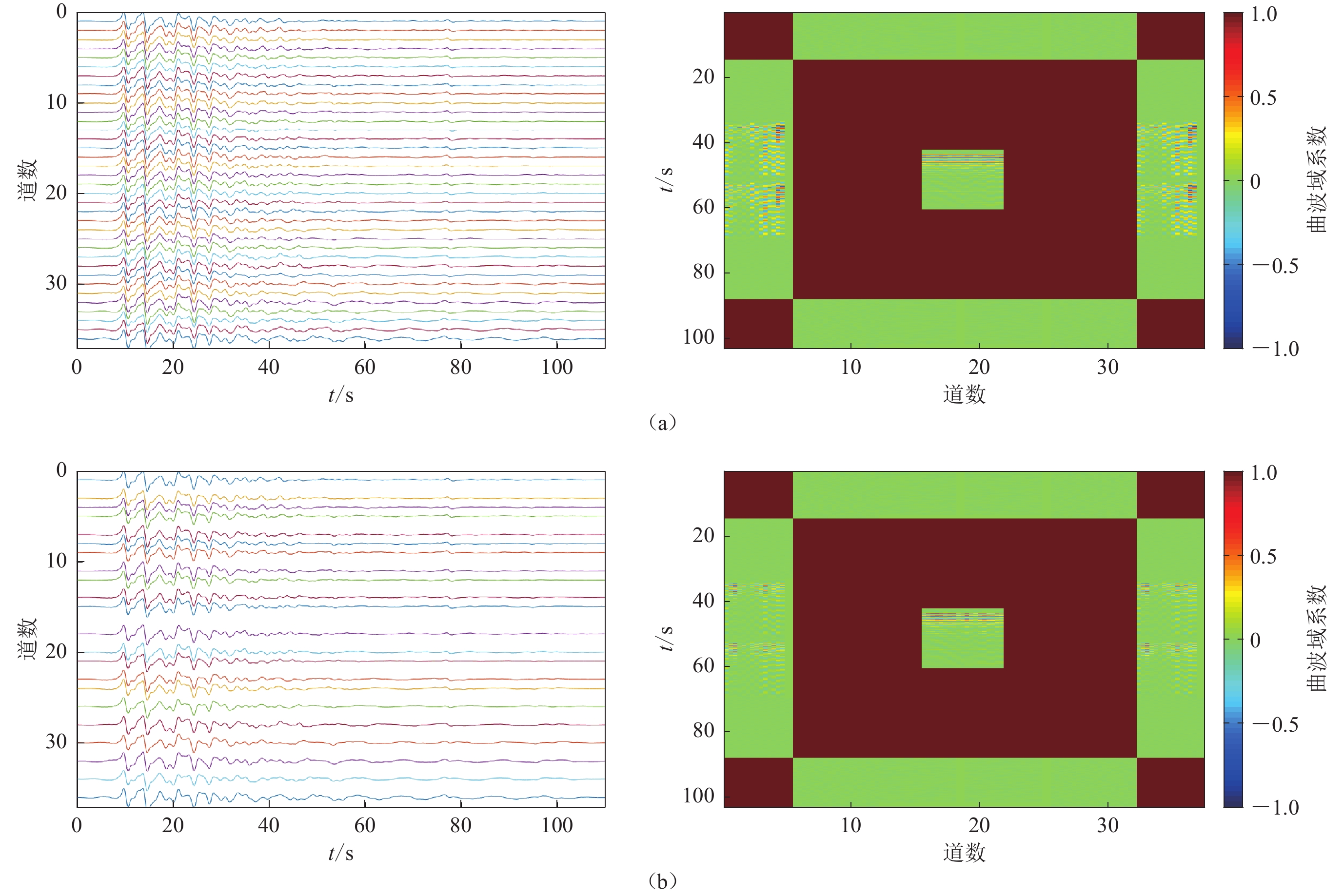
图 2 模拟地震数据和重建地震数据对比Figure 2. Comparison of the simulated seismic data with the reconstruction data（a） NM01；（b） NM02；（c） NM03；（d） NM04图3给出了模拟天然地震数据及其曲波域系数分布。图3a为完整的和随机采样60%的天然地震数据，图3b为其曲波域系数，图片中心表示低频系数，外围表示不同方向的高频系数。可以看到当随机采样地震数据变换到曲波域后，能量未很好地聚焦，曲波域系数较小。
![]()
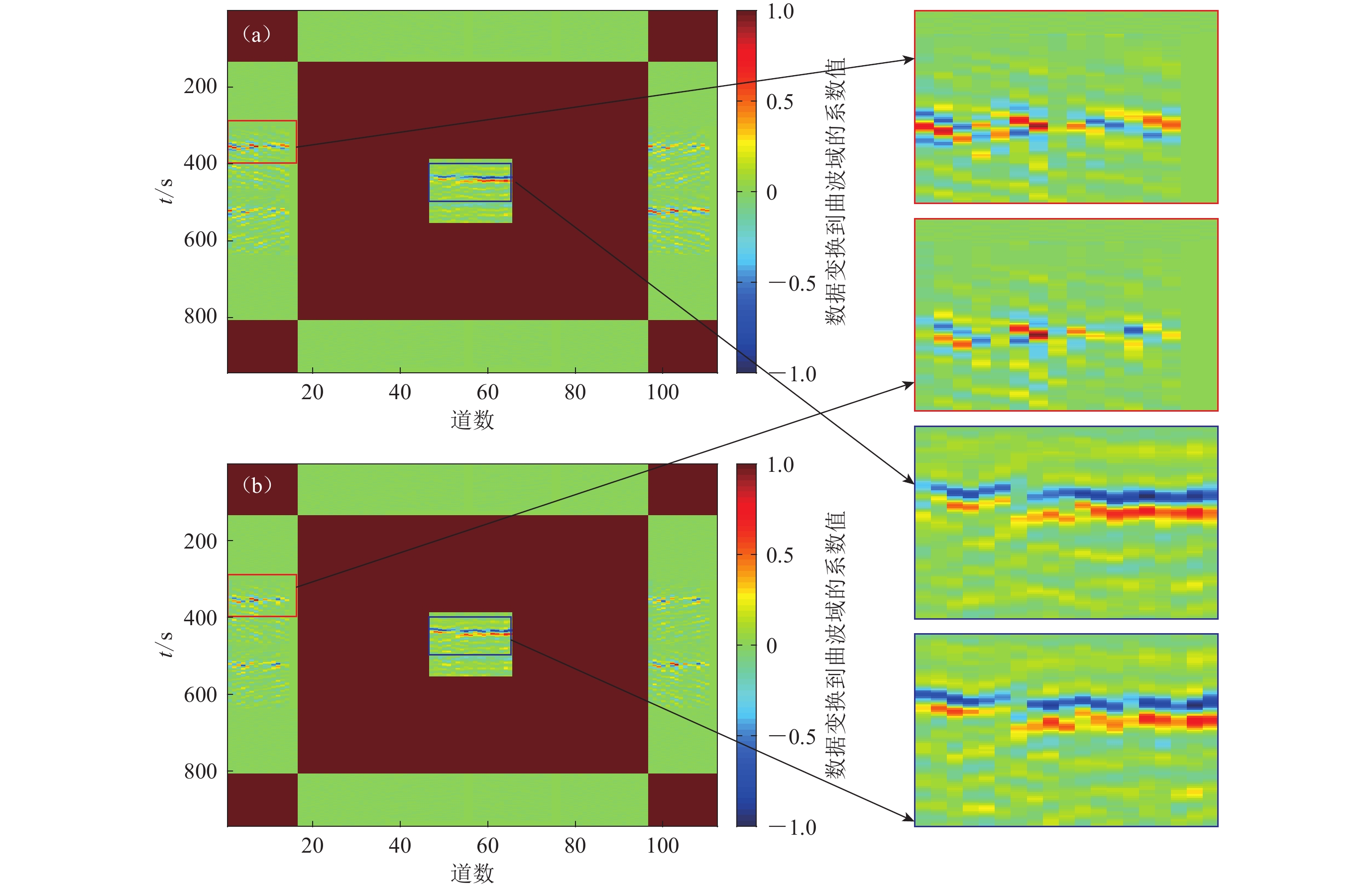
图 3 完整的（a）和随机采样60%的（b）模拟地震数据（左）及其曲波域系数分布（右）Figure 3. Complete （a） and 60% random sampling （b） simulated seismic data （left） and distribution of their curvelet coefficients （right）图4为部分天然地震真实数据的曲波域系数。由于本文用于计算的数据为P波到时，为了展示得更清晰，截取了只包含P波到时部分的数据进行再次展示。线框中红色表示正振幅，蓝色表示负振幅。对比同色线框可以发现，较大系数分布（深颜色部分）具有一定的相似性，且较大曲波域系数携带P波到时信息，因此可以采用本文方法重建天然地震P波到时数据。
![]()
图 4 部分天然地震完整的真实数据（a）和随机采样60%的真实数据（b）的曲波域系数分布图中红色和蓝色线框分别表示低频和高频P波到时的曲波域系数Figure 4. Distribution of curvelet domain coefficients of complete （a） and 60% random sampling （b） partial natural earthquake observed dataThe red and blue boxes represent the curvelet domain coefficients of low and high frequency P-wave arrival time2. 天然地震数据P波重建和到时分析
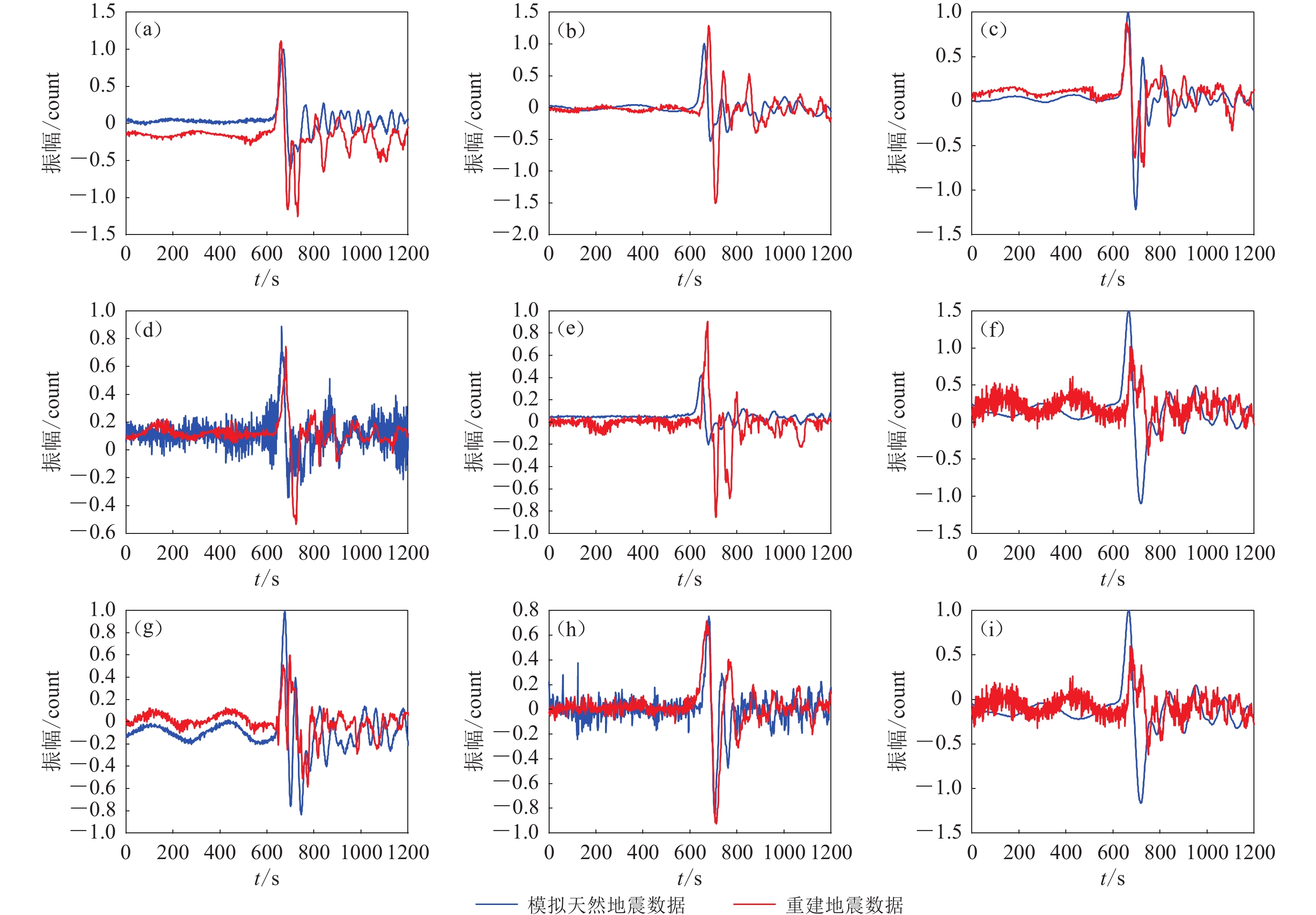
在验证了模拟数据后，我们开展了天然地震远震波形数据重建的试验（图5）。从图5可以看出，地震P波波形被很好地重构出来。与模拟地震数据相比，实际天然地震观测数据在采集的过程中会包含各种各样的噪声信号，其中一些规则相干噪声的信号通常会出现放大或增强的现象（图5c），但有效的地震观测信号均能较好地实现重建。为了能够清晰地展示重建效果，选取九个地震台站记录，对比分析重建后的地震数据与每个地震台站的实际观测数据（图6），可见：图6a，6c，6e，6f和6i两者吻合效果好；图6b与图6h重建过程中同时压制了噪声干扰；图6b与图6a在P波初至到时上重建效果好，但重建数据振幅出现了偏差。总体而言，这两者能够达到很好的吻合效果，尤其是在P波初动波形方面吻合得很好，说明该研究方法可以较好地实现缺失地震数据的重建。
![]()
图 5 天然地震P波波形数据重建试验（a） 内蒙古流动台阵记录到的M5.7地震的原始P波数据；（b） 对原始波形数据进行随机采样得到的记录，随机采样率为65%；（c） 对采样记录进行重建得到的地震波形记录Figure 5. The reconstruction test of P-waveform data for natural earthquakes![]()
图 6 内蒙古流动台阵部分台站实际记录到的地震数据与重建数据的对比Figure 6. Comparison of the real recorded seismic data from partial stations of portable array at Inner Mongolia with the reconstruction data（a） NM02；（b） NM08；（c） NM12；（d） NM13；（e） NM18；（f） NM20；（g） NM21；（h） NM24；（i） NM263. 基于层析成像验证压缩感知数据重建方法的有效性
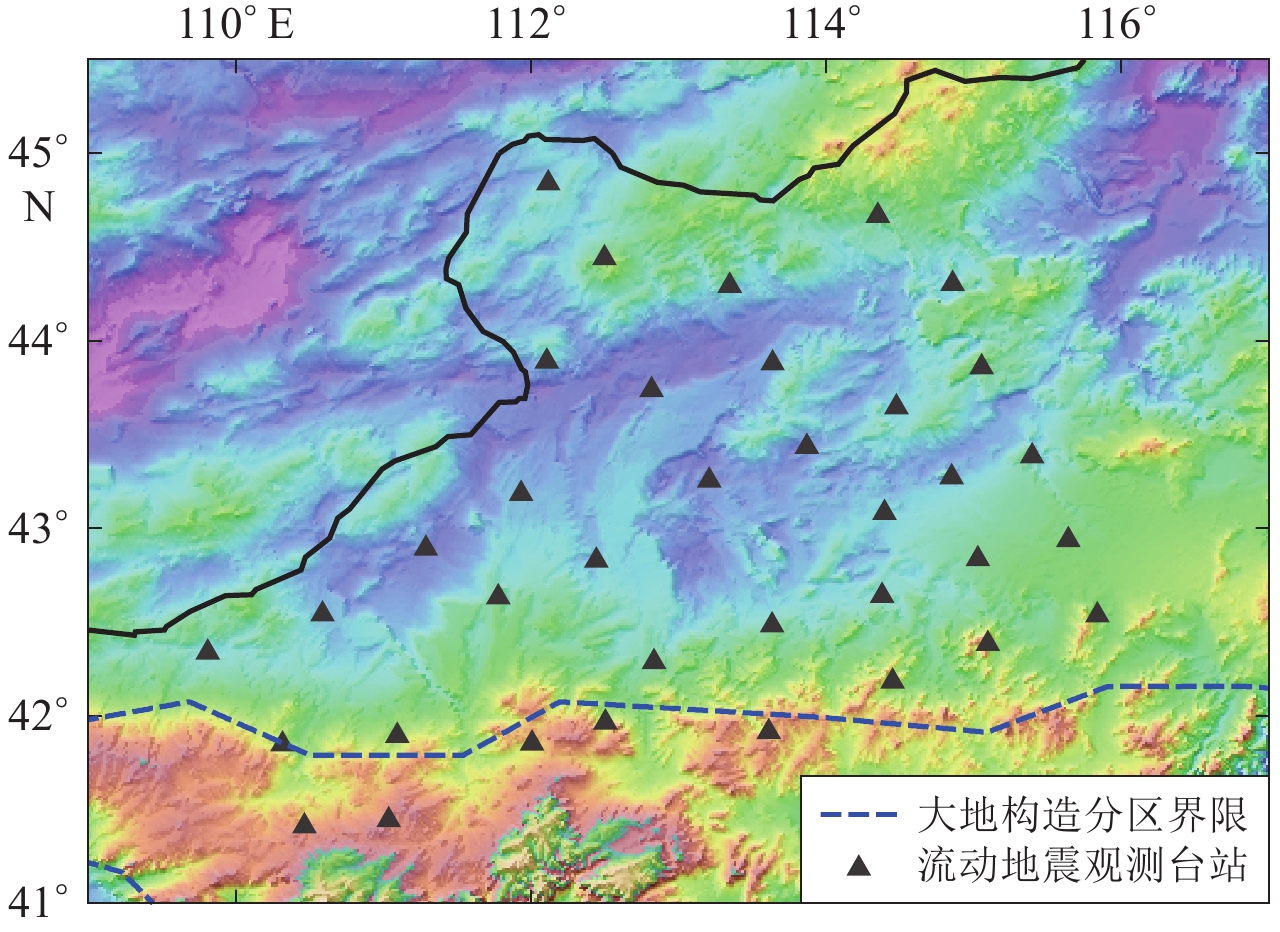
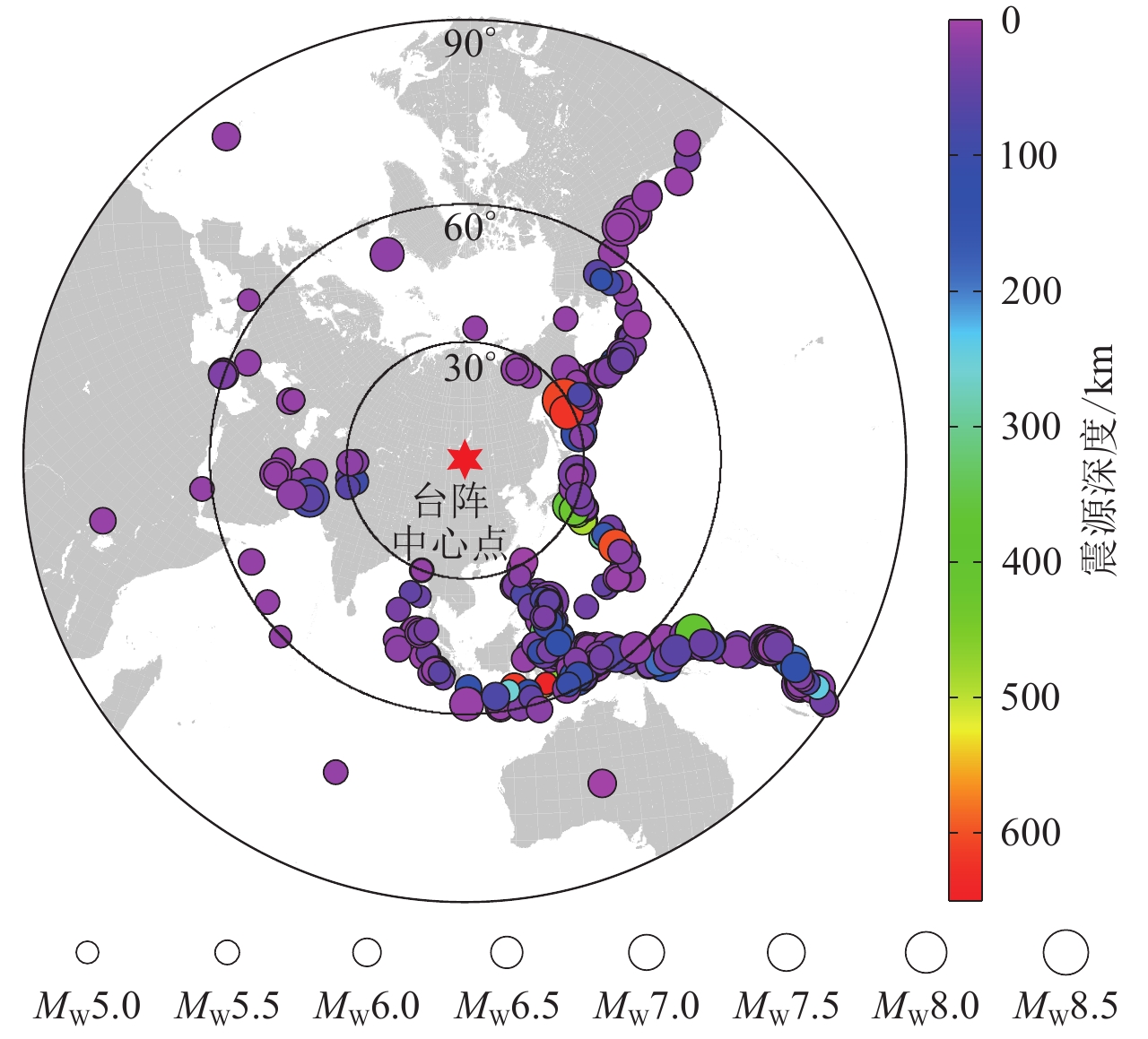
利用布设在内蒙古地区的36个流动地震观测台站（图7）于2012年10月至2014年3月期间所记录到的远震P波走时波形数据，基于以下三个原则对远震事件进行筛选：① 远震事件的震中距应处于30°—90°；② 远震事件的震级应不小于M5.5 ；③ 每个远震事件至少被26个地震台站记录到。
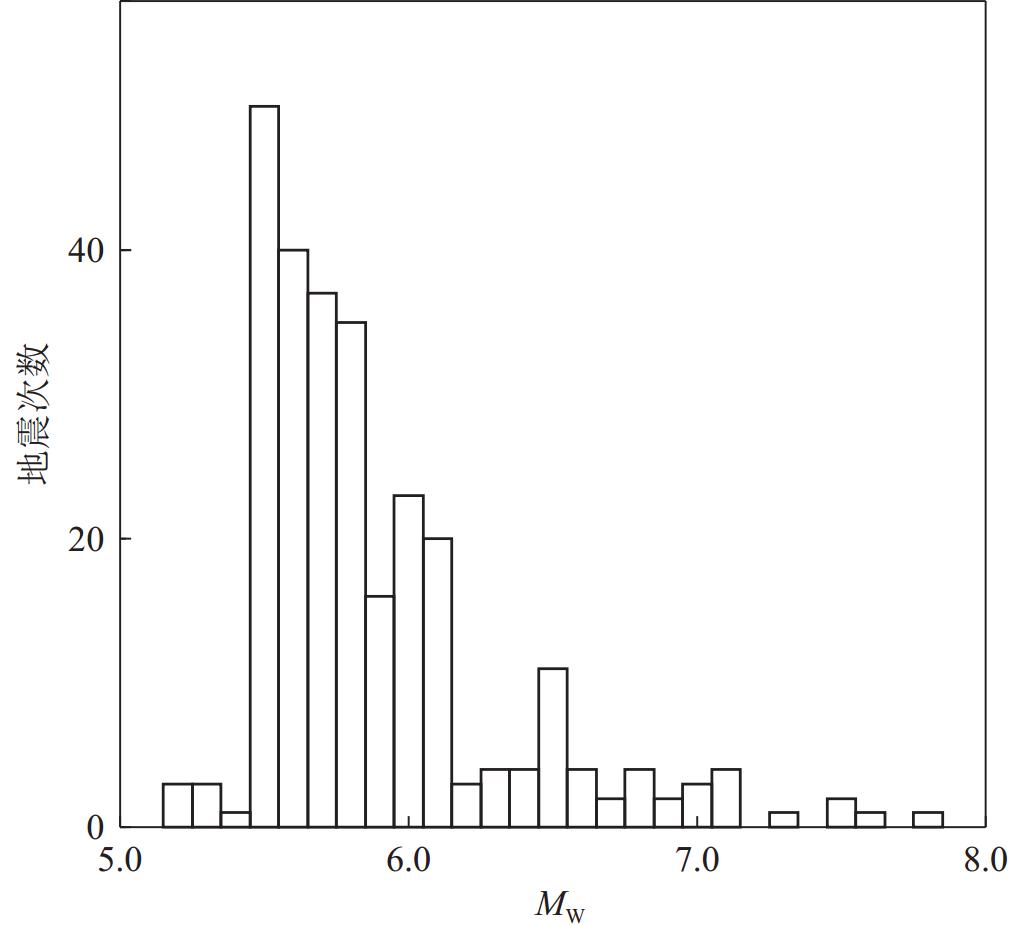
首先对选取的地震数据进行随机采样，采样率为50%，并对单个地震事件的采样数据进行数据重建；然后对波形数据（包括原始数据、采样数据和重建数据）进行预处理，滤波采用0.02—0.1 Hz频段；最后采用波形互相关方法拾取P波走时残差，共计得到9 000条原始P波走时数据，4 500条采样数据和9 000条重建后的地震数据，有效远震事件274个（图8），所选用的地震事件震级优势分布集中在M5.5—6.5 （图9）。
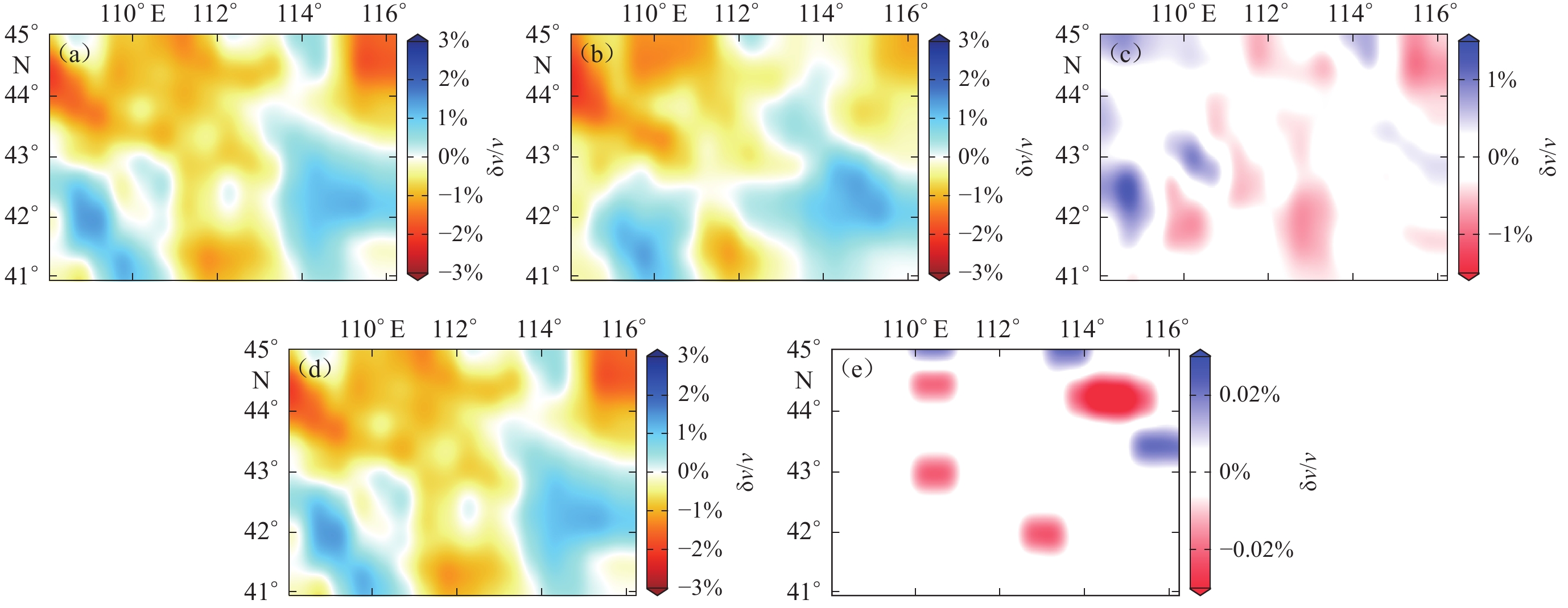
本文采用走时层析成像的方法对所获取的原始数据、采样数据和重建后的地震数据分别进行速度结构反演。图10a，10b，10d分别是对原始数据、采样数据和重建数据反演所获得的研究区位于600 km深度的水平切面，图10c表明数据缺失时计算的层析成像速度与使用完整数据计算的层析成像速度差别很大，图10e表明重建数据计算的层析成像结果与完整数据计算的层析成像结果相对误差在千分之二以内。图11a，11b，11d分别是原始数据、采样数据和重建数据反演获得的在同一位置（44°N，110°E）和（42°N，115°E）的垂直切面。由图10和图11不难发现，利用原始数据和重建数据获得的走时残差所反演的层析成像结果具有高度的相似性，主要的高低速异常的空间位置和形态具有高度一致性。这说明压缩感知理论重建方法可以由采样数据恢复出原始数据的成像结果。
![]()
图 10 600 km深度的P波速度扰动结果水平切片（a） 原始数据图；（b） 采样数据；（c） 图（a）与图（b）反演结果的差；（d） 重建数据；（e） 图（a）与图（d）反演结果的差Figure 10. Horizontal slices of P-wave velocity disturbance results at a depth of 600 km（a） Original data；（b） The sampled data；（c） The difference between the inversion results of Fig.（a） and Fig.（b）；（d） Reconstruction data； （e） The difference between the inversion results of Fig.（a） and Fig.（d）![]()
图 11 P波速度纵剖面示意图（a） 原始数据；（b） 采样数据；（c） 图（a）与图（b）反演结果的差；（d） 重建数据；（e） 图（a）与图（d）反演结果的差Figure 11. Schematic diagram of P-wave velocity vertical profile（a） Original data；（b） The sampled data；（c） The difference between the inversion results of Fig.（a） and Fig.（b）；（d） Reconstruction data； （e） The difference between the inversion results of Fig.（a） and Fig.（d）4. 结论
本文针对天然地震远震事件的P波到时数据，利用曲波变换建立了基于L1范数的正则化反演模型，并采用迭代收缩阈值算法（ISTA）求解该模型，之后将该方法应用于内蒙古地区流动地震台阵观测的远震数据数据，并拾取重建后的P波到时数据，最后开展远震层析成像以验证该方法的有效性。
天然地震数据重建试验表明天然地震数据在曲波变换中具有稀疏的表达，基于地震数据本身，在地震数据缺失或者天然地震观测数据不完备时，可以采用压缩感知理论算法完成地震数据的重建工作，同时可利用该方法对信噪比较差的数据进行重建，可获取高信噪比的地震数据。基于内蒙古地区流动地震台阵的三维P波成像实验表明了基于压缩感知理论方法的数据重建技术可以提高地震层析成像的分辨率。研究结果还表明了压缩感知理论在天然地震数据中具有潜在的应用价值，为后续探索天然地震新的台阵观测方式和数据采集提供了研究思路。
需要指出的是，本文采用的是二维数据重建方法获取的地震P波到时数据，基于获取的到时数据开展的三维P波层析成像在三维天然地震数据重建方面还存在改进和完善的空间，三维天然地震数据重建是后续的研究方向。
中国地震局地球物理研究所“国家数字测震台网数据备份中心（doi:10.11998/SeisDmc/SN）”、中国地震局地球物理研究所在内蒙古布设的临时台网提供了连续波形数据，四川省地震局、中国地震局成都青藏高原地震研究所李大虎研究员为地震数据处理和分析提出了宝贵的意见，中国地震局地球物理研究所张旭博士提供了天然地震数值模拟结果，作者在此一并表示感谢。
-
![]()
图 1 模拟天然地震数据重建
（a） 原始数据；（b） 采样数据；（c） 重建数据
Figure 1. Reconstruction of simulated natural earthquake data
（a） Simulation data；（b） Sampling data；（c） Reconstruction data
![]()
图 2 模拟地震数据和重建地震数据对比
Figure 2. Comparison of the simulated seismic data with the reconstruction data
（a） NM01；（b） NM02；（c） NM03；（d） NM04
![]()
图 3 完整的（a）和随机采样60%的（b）模拟地震数据（左）及其曲波域系数分布（右）
Figure 3. Complete （a） and 60% random sampling （b） simulated seismic data （left） and distribution of their curvelet coefficients （right）
![]()
图 4 部分天然地震完整的真实数据（a）和随机采样60%的真实数据（b）的曲波域系数分布
图中红色和蓝色线框分别表示低频和高频P波到时的曲波域系数
Figure 4. Distribution of curvelet domain coefficients of complete （a） and 60% random sampling （b） partial natural earthquake observed data
The red and blue boxes represent the curvelet domain coefficients of low and high frequency P-wave arrival time
![]()
图 5 天然地震P波波形数据重建试验
（a） 内蒙古流动台阵记录到的M5.7地震的原始P波数据；（b） 对原始波形数据进行随机采样得到的记录，随机采样率为65%；（c） 对采样记录进行重建得到的地震波形记录
Figure 5. The reconstruction test of P-waveform data for natural earthquakes
（a） P-waveform data of the M5.7 earthquake recorded by the Inner Mongolia mobile array；（b） The records obtained by random sampling to the data of Fig.5a with a rate of 65%；（c） Seismic waveform records obtained by the reconstruction of Fig.5b
![]()
图 6 内蒙古流动台阵部分台站实际记录到的地震数据与重建数据的对比
Figure 6. Comparison of the real recorded seismic data from partial stations of portable array at Inner Mongolia with the reconstruction data
（a） NM02；（b） NM08；（c） NM12；（d） NM13；（e） NM18；（f） NM20；（g） NM21；（h） NM24；（i） NM26
![]()
图 10 600 km深度的P波速度扰动结果水平切片
（a） 原始数据图；（b） 采样数据；（c） 图（a）与图（b）反演结果的差；（d） 重建数据；（e） 图（a）与图（d）反演结果的差
Figure 10. Horizontal slices of P-wave velocity disturbance results at a depth of 600 km
（a） Original data；（b） The sampled data；（c） The difference between the inversion results of Fig.（a） and Fig.（b）；（d） Reconstruction data； （e） The difference between the inversion results of Fig.（a） and Fig.（d）
![]()
图 11 P波速度纵剖面示意图
（a） 原始数据；（b） 采样数据；（c） 图（a）与图（b）反演结果的差；（d） 重建数据；（e） 图（a）与图（d）反演结果的差
Figure 11. Schematic diagram of P-wave velocity vertical profile
（a） Original data；（b） The sampled data；（c） The difference between the inversion results of Fig.（a） and Fig.（b）；（d） Reconstruction data； （e） The difference between the inversion results of Fig.（a） and Fig.（d）
-
白兰淑,刘伊克,卢回忆,王一博,常旭. 2014. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报,57(9):2937–2945. doi: 10.6038/cjg20140919 Bai L S,Liu Y K,Lu H Y,Wang Y B,Chang X. 2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics,57(9):2937–2945 (in Chinese).
白兰淑,吴庆举,张瑞青. 2022. 压缩感知高分辨率接收函数叠加成像及其应用[J]. 地球物理学报,65(11):4354–4368. doi: 10.6038/cjg2022P0419 Bai L S,Wu Q J,Zhang R Q. 2022. High-resolution receiver function imaging based on compressive sensing and its application[J]. Chinese Journal of Geophysics,65(11):4354–4368 (in Chinese).
曹静杰,王彦飞,杨长春. 2012. 地震数据压缩重构的正则化与零范数稀疏最优化方法[J]. 地球物理学报,55(2):596–607. doi: 10.6038/j.issn.0001-5733.2012.02.022 Cao J J,Wang Y F,Yang C C. 2012. Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization[J]. Chinese Journal of Geophysics,55(2):596–607 (in Chinese).
曹静杰,王尚旭,李文斌. 2017. 基于一种三维低冗余曲波变换和压缩感知理论的地震数据重建[J]. 中国石油大学学报(自然科学版),41(5):61–68. doi: 10.3969/j.issn.1673-5005.2017.05.007 Cao J J,Wang S X,Li W B. 2017. Seismic reconstruction with 3D low-redundancy curvelet transform and compressed sensing theory[J]. Journal of China University of Petroleum (Edition of Natural Science),41(5):61–68 (in Chinese).
曹静杰,杨志权,杨歧焱. 2020. 一种基于压缩感知的地震数据重建方法及其在城市活断层地震勘探中的应用[J]. 地球物理学进展,35(4):1545–1551. doi: 10.6038/pg2020DD0267 Cao J J,Yang Z Q,Yang Q Y. 2020. Compressive sensing based seismic reconstruction method and its application to seismic exploration of urban active faults[J]. Progress in Geophysics,35(4):1545–1551 (in Chinese).
付明柏. 2013. 基于异质矩阵完全的缺失数据恢复混合集成算法[J]. 云南师范大学学报(自然科学版),33(6):67–72. Fu M B. 2013. Mixed ensemble heterogeneous matrix completion for missing value estimation[J]. Journal of Yunnan Normal University (Natural Sciences Edition),33(6):67–72 (in Chinese).
孔德辉. 2017. 基于压缩感知的地震数据重建及若干问题研究[D]. 成都:电子科技大学:1–11. Kong D H. 2017. Research on Some Issues of Seismic Data Reconstruction Based on Compressed Sensing[D]. Chengdu:University of Electronic Science and Technology of China:1–11 (in Chinese).
赵杨. 2018. 地震体波走时与重力联合反演研究及在南北地震带南段的应用[D]. 北京:中国地质大学(北京):1–9. Zhao Y. 2018. Joint Inversion of Seismic Traveltime and Gravity Data and Its Application in Imaging Crustal Structure Around Southern Section of North-South Earthquake Belt[D]. Beijing:China University of Geosciences (Beijing):1–9 (in Chinese).
郑雪辰. 2019. 基于压缩感知理论和SPGL1算法的地震数据重建[D]. 西安:长安大学:1–9. Zheng X C. 2019. Seismic Data Reconstruction Based on Compressive Sensing and SPGL1 Algorithm[D]. Xi’an:Chang’an University:1–9 (in Chinese).
Bai L S,Lu H Y,Liu Y K. 2020. High-efficiency observations:Compressive sensing and recovery of seismic waveform data[J]. Pure Appl Geophys,177(1):469–485. doi: 10.1007/s00024-018-2070-z
Candès E,Demanet L,Donoho D,Ying L X. 2006a. Fast discrete curvelet transforms[J]. Multiscale Model Simul,5(3):861–899. doi: 10.1137/05064182X
Candès E J,Romberg J,Tao T. 2006b. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inform Theory,52(2):489–509. doi: 10.1109/TIT.2005.862083
Cao J J,Wang Y F,Wang B F. 2015. Accelerating seismic interpolation with a gradient projection method based on tight frame property of curvelet[J]. Explor Geophys,46(3):253–260. doi: 10.1071/EG14016
Daubechies I,Defrise M,De Mol C. 2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Commun Pure Appl Math,57(11):1413–1457. doi: 10.1002/cpa.20042
Donoho D L. 2006. Compressed sensing[J]. IEEE Trans Inform Theory,52(4):1289–1306. doi: 10.1109/TIT.2006.871582
Herrmann F J,Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames[J]. Geophys J Int,173(1):233–248. doi: 10.1111/j.1365-246X.2007.03698.x
Ismael V R,Mauricio S,Yu J G. 2012. A compressive sensing framework for seismic source parameter estimation[J]. Geophys J Int,191(3):1226–1236
Rawlinson N,Pozgay S,Fishwick S. 2010. Seismic tomography:A window into deep Earth[J]. Phys Earth Planet Inter,178(3/4):101–135.
Wang B,Chen X,Li J,Cao J. 2016. An improved weighted projection onto convex sets methods for seismic data interpolation and denoising[J]. IEEE J STARS,9:228–235.
Wang R J. 1999. A simple orthonormalization method for stable and efficient computation of Green’s functions[J]. Bull Seismol Soc Am,89(3):733–741. doi: 10.1785/BSSA0890030733
Zhang H L,Song S,Liu T Y. 2007. The ridgelet transform with non-linear threshold for seismic noise attenuation in marine carbonates[J]. Appl Geophys,4(4):271–275. doi: 10.1007/s11770-007-0027-6
Zhou Q B,Gao J H,Wang Z G. 2015. Sparse spike deconvolution of seismic data using trust-region based SQP algorithm[J]. J Comput Acoust,23(4):1540002. doi: 10.1142/S0218396X15400020
下载:
计量
- 文章访问数: 229
- HTML全文浏览量: 150
- PDF下载量: 177
