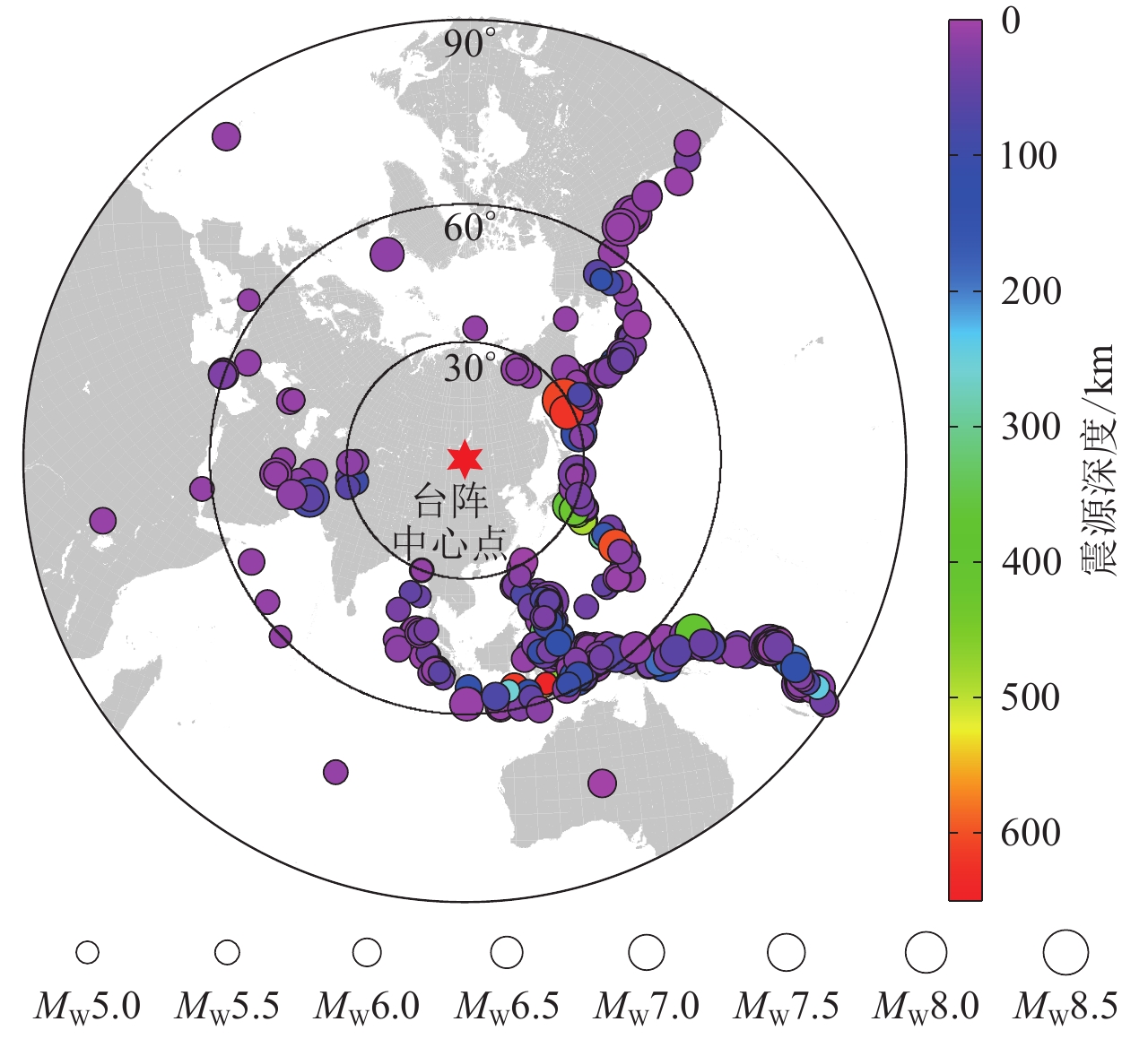
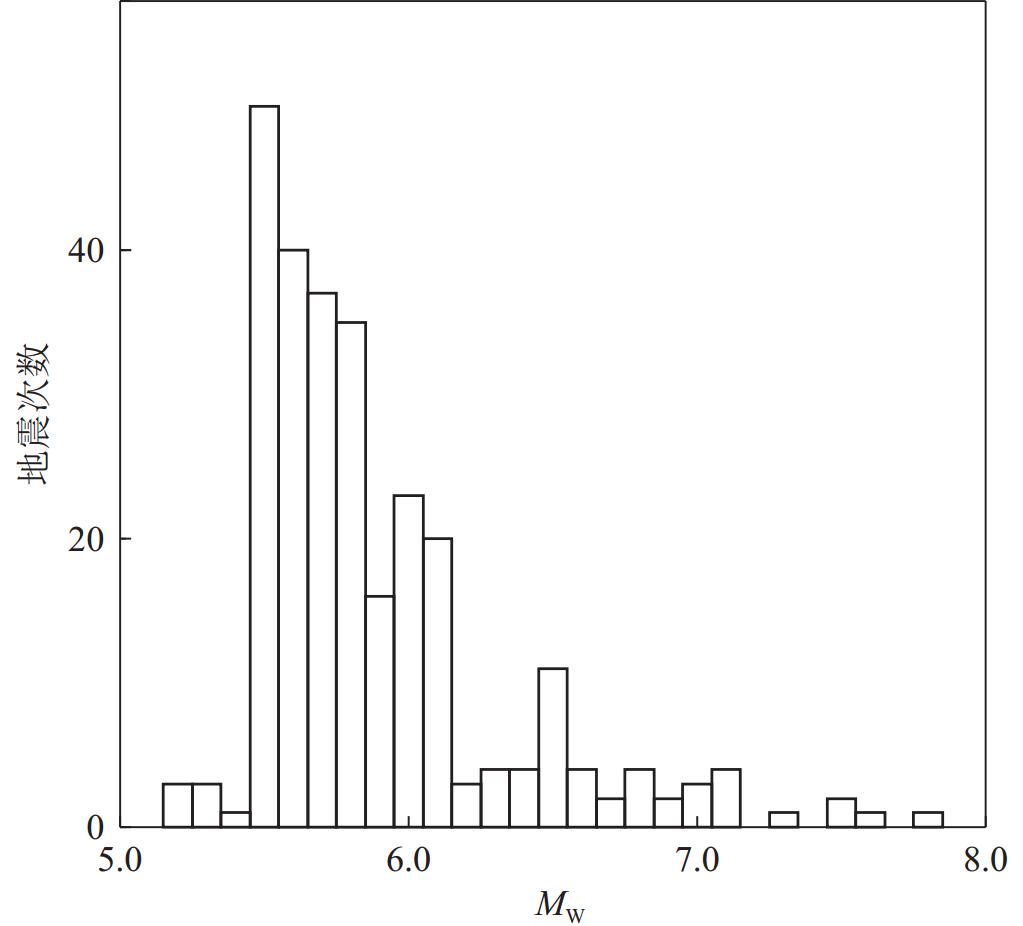
Teleseismic P-wave data reconstruction based on compressive sensing theory
-
摘要:
本文将基于压缩感知理论的地震观测数据重建方法用于天然远震事件的P波到时处理之中,基于曲波(curvelet)变换,建立基于L1范数的正则化反演模型,并采用迭代收缩阈值算法(ISTA)求解该模型。针对在内蒙古布设的流动地震台阵记录到的远震波形数据,对其进行稀疏采样,采用稀疏反演重建方法对欠采样数据进行重建,并拾取重建数据的P波到时,之后开展远震P波层析成像进行验证。研究结果表明,远震天然地震观测数据在曲波变换中表现出稀疏性,可利用压缩感知方法实现远震P波数据的完备化处理。基于内蒙古流动地震台阵数据三维P波成像也表明,基于压缩感知的数据重建技术可以提高地震层析成像的分辨率,且压缩感知采集技术在天然地震研究中具有潜在的应用价值。
Abstract:The non-uniformity and incompleteness of seismic data in space have long been one of the significant challenges affecting seismic imaging. The factors that cause the non-uniform spatial distribution of seismic data are primarily twofold: Firstly, the non-uniform distribution of earthquakes, which are the sources of seismic waves; Secondly, the non-uniform distribution of seismic stations used to record these waves. In areas where stations are difficult to built, such as mountainous regions and offshore locations, uniform array deployment becomes impractical. These factors lead to the acquisition of non-uniform and incomplete data, thereby reducing the resolution and accuracy of the imaging results.
The core principle of compressed sensing theory is to exploit the sparse nature of the signal and then employ a non-linear reconstruction algorithm to recover the original signal. Since seismic wavefields exhibit continuity, then missing or irregularly sampled seismic data can potentially be recovered through compressed sensing techniques. In the time domain, seismic observation data usually contain rich frequency information. However, due to the filtering effects of subsurface layers, the bandwidth of the actual recorded seismic data is limited, and the data exhibit sparsity in the frequency domain. Based on this characteristic, under limited acquisition conditions, the reconstruction of missing seismic data utilizing compressed sensing theory can, to some extent, mitigate the problem of insufficient seismic data coverage.
In oil and gas seismic exploration, data reconstruction methods based on compressed sensing theory have been widely applied to address the issue of insufficient sampling. However, relevant discussions are not yet common in the acquisition and processing of natural earthquake data. In fact, due to environmental and site constraints, the acquisition of natural earthquake data also suffers missing and irregular sampling issues. Moreover, owing to the irregular distribution of acquisition stations, the reconstruction of natural earthquake data encounters greater challenges. Natural earthquake waveforms are more complex, and proposing a reliable scheme for reconstructing natural earthquake data under the condition of irregularly distributed acquisition stations is a relatively difficult problem.
For artificial seismic exploration data reconstruction, the trace spacing is small, and the waveforms of adjacent traces exhibit good consistency. In Chinese continental natural earthquake observation stations, the minimum station spacing is less than 30 km, and the teleseismic waveforms recorded at different stations also exhibit certain similarities. This study commences with natural teleseismic observation data, draws upon the experience of artificial seismic data reconstruction, and attempts to conduct research on the reconstruction of teleseismic data. Relevant experimental verifications have been carried out.
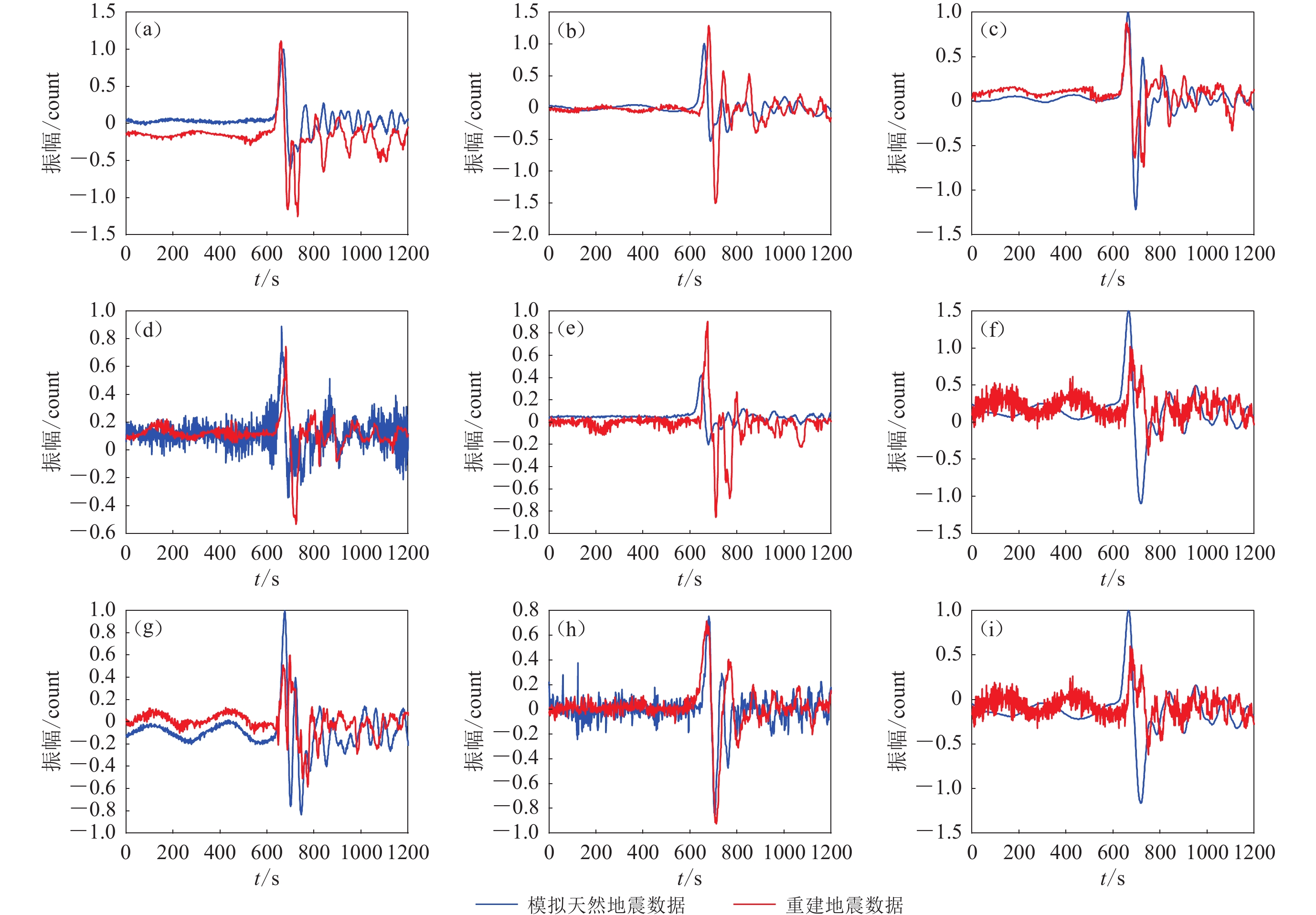
To verify the reconstruction effect of the algorithm, we first use the reflectivity method to calculate the theoretical seismogram, simulating the teleseismic P-wave data recorded by the Inner Mongolia movable array. Thirty-six seismic stations receive the data, with a sampling interval of 2 ms and 5501 sampling points. The simulated seismic data are obtained through calculation of seismic travel time, and the missing teleseismic P-wave data are recovered, verifying the effectiveness of the method. Compared with the original record, the reconstructed seismic record signals can restore the waveform relatively well; the reconstructed result is generally consistent with the original record. In terms of amplitude, the reconstructed result is significantly smaller, and the frequency is also higher, which shows that the reconstruction method has the effect of suppressing random noise. Simultaneously, there are certain differences in the waveforms across different stations, and the analysis suggests that the number of iterations for certain station data is insufficient, or there are discrepancies in parameter adjustments.
We applied the seismic data reconstruction method that based on compressed sensing to process P-wave arrival times of teleseismic events. Firstly, the curvelet transform is utilized as a sparse transform, and a regularized inversion model based on the L1 norm is established. The iterative shrinkage-thresholding algorithm (ISTA) is employed to solve this model. Subsequently, the compressed sensing theory is applied to the reconstruction of teleseismic data observed by the portable seismic array in the Inner Mongolia region. On this basis, data reconstruction is performed on the acquired real earthquake data, and the reconstructed P-wave arrival time data are picked to verify the effectiveness of the method through teleseismic tomography.
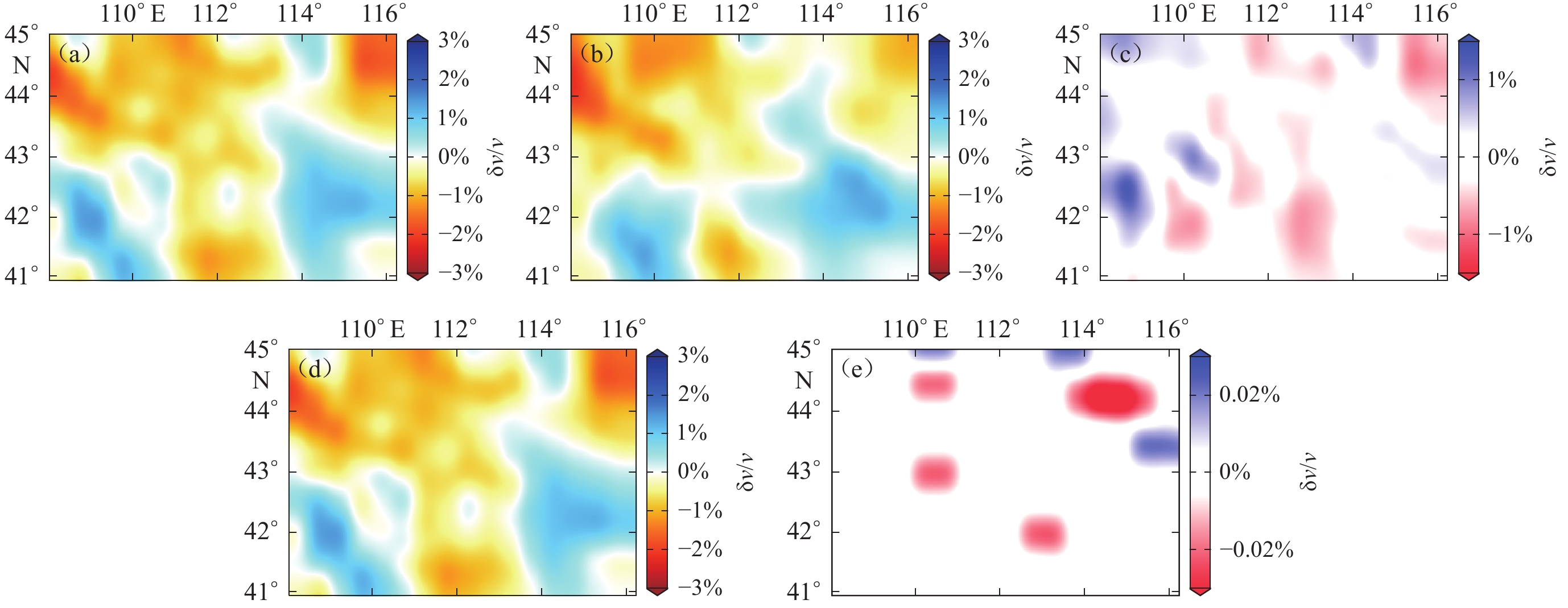
The practice of natural earthquake data reconstruction demonstrates that natural earthquake data exhibit a sparse representation in the curvelet transform domain. Based on the seismic data itself, when seismic data are missing or the natural earthquake observation data are incomplete, the compressed sensing theory can be employed to reconstruct the seismic data. Concurrently, this method can be utilized to reconstruct data with poor signal-to-noise ratio and obtain high signal-to-noise ratio seismic data. In this study, the fast marching teleseismic tomography (FMTT) method is used to invert the velocity structure from the original data, sampled data, and reconstructed seismic data, respectively. The results indicate that when data are missing, the calculated tomographic velocity structure deviates significantly from that calculated with complete data. The relative error between the tomographic result obtained from the reconstructed data and that from the complete data is within 0.02%. The vertical cross-section shows that the tomographic results obtained from the original data and reconstructed data exhibit highly similar travel time residuals, and the spatial positions and shapes of the main high and low velocity anomaly zones are highly consistent. This signifies that the compressed sensing based theory reconstruction method can recover the imaging results from the sampled data. The practice of three-dimensional P-wave imaging proves that the data reconstruction technique based on compressed sensing theory can improve the resolution of seismic tomography. The results also demonstrate the potential application value of compressed sensing acquisition technology in natural earthquake data, which can provide and broaden the research ideas for exploring new array observation methods and data acquisition strategies for natural earthquakes.
-
Keywords:
- compressive sensing /
- curvelet transform /
- teleseismic P-wave /
- seismic reconstruction /
- L1 norm
-
-
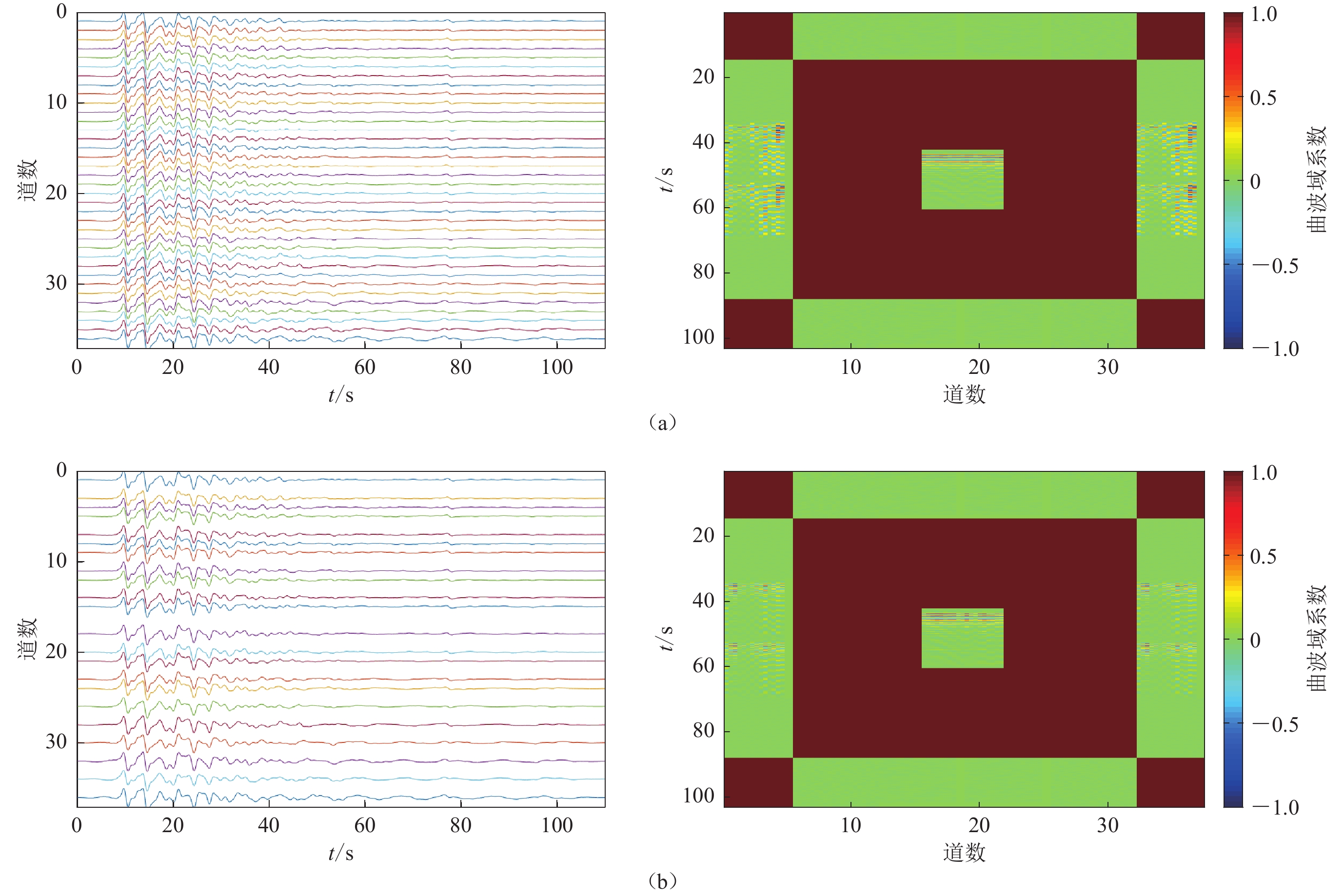
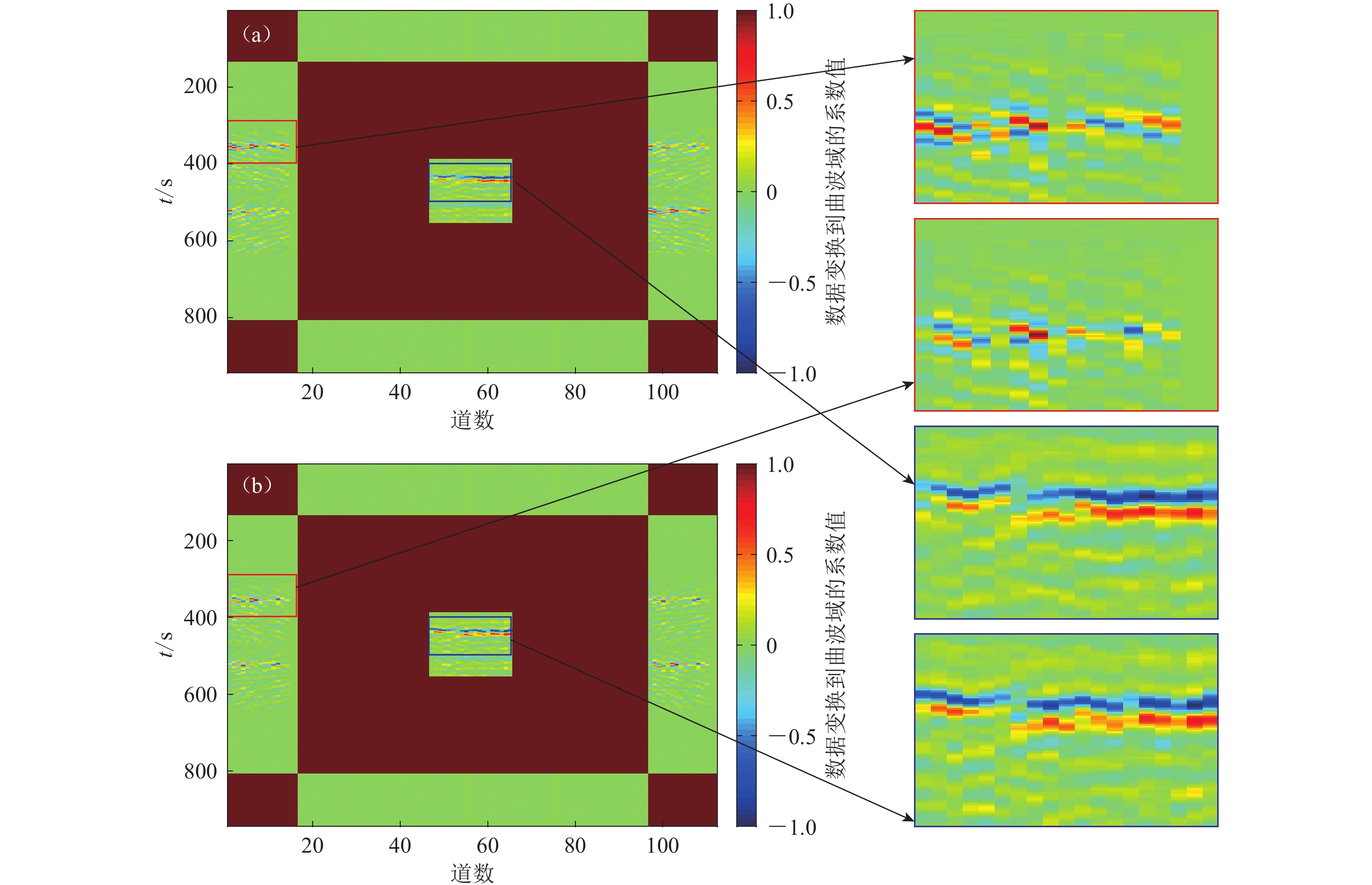
图 4 部分天然地震完整的真实数据(a)和随机采样60%的真实数据(b)的曲波域系数分布
图中红色和蓝色线框分别表示低频和高频P波到时的曲波域系数
Figure 4. Distribution of curvelet domain coefficients of complete (a) and 60% random sampling (b) partial natural earthquake observed data
The red and blue boxes represent the curvelet domain coefficients of low and high frequency P-wave arrival time
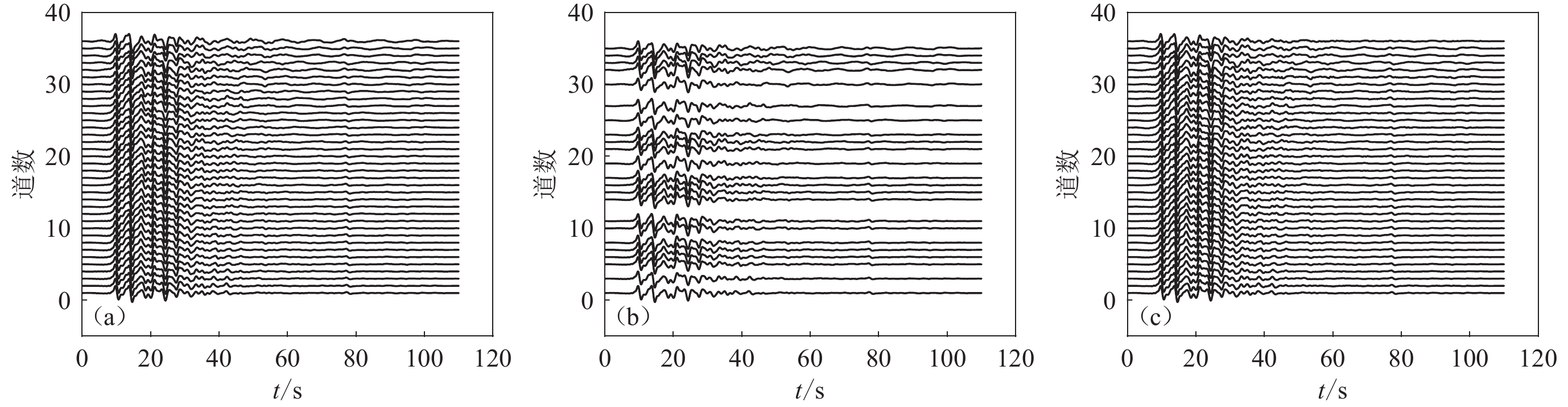
图 5 天然地震P波波形数据重建试验
(a) 内蒙古流动台阵记录到的M5.7地震的原始P波数据;(b) 对原始波形数据进行随机采样得到的记录,随机采样率为65%;(c) 对采样记录进行重建得到的地震波形记录
Figure 5. The reconstruction test of P-waveform data for natural earthquakes
(a) P-waveform data of the M5.7 earthquake recorded by the Inner Mongolia mobile array;(b) The records obtained by random sampling to the data of Fig.5a with a rate of 65%;(c) Seismic waveform records obtained by the reconstruction of Fig.5b
图 10 600 km深度的P波速度扰动结果水平切片
(a) 原始数据图;(b) 采样数据;(c) 图(a)与图(b)反演结果的差;(d) 重建数据;(e) 图(a)与图(d)反演结果的差
Figure 10. Horizontal slices of P-wave velocity disturbance results at a depth of 600 km
(a) Original data;(b) The sampled data;(c) The difference between the inversion results of Fig.(a) and Fig.(b);(d) Reconstruction data; (e) The difference between the inversion results of Fig.(a) and Fig.(d)
图 11 P波速度纵剖面示意图
(a) 原始数据;(b) 采样数据;(c) 图(a)与图(b)反演结果的差;(d) 重建数据;(e) 图(a)与图(d)反演结果的差
Figure 11. Schematic diagram of P-wave velocity vertical profile
(a) Original data;(b) The sampled data;(c) The difference between the inversion results of Fig.(a) and Fig.(b);(d) Reconstruction data; (e) The difference between the inversion results of Fig.(a) and Fig.(d)
-
白兰淑,刘伊克,卢回忆,王一博,常旭. 2014. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报,57(9):2937–2945. doi: 10.6038/cjg20140919 Bai L S,Liu Y K,Lu H Y,Wang Y B,Chang X. 2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics,57(9):2937–2945 (in Chinese).
白兰淑,吴庆举,张瑞青. 2022. 压缩感知高分辨率接收函数叠加成像及其应用[J]. 地球物理学报,65(11):4354–4368. doi: 10.6038/cjg2022P0419 Bai L S,Wu Q J,Zhang R Q. 2022. High-resolution receiver function imaging based on compressive sensing and its application[J]. Chinese Journal of Geophysics,65(11):4354–4368 (in Chinese).
曹静杰,王彦飞,杨长春. 2012. 地震数据压缩重构的正则化与零范数稀疏最优化方法[J]. 地球物理学报,55(2):596–607. doi: 10.6038/j.issn.0001-5733.2012.02.022 Cao J J,Wang Y F,Yang C C. 2012. Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization[J]. Chinese Journal of Geophysics,55(2):596–607 (in Chinese).
曹静杰,王尚旭,李文斌. 2017. 基于一种三维低冗余曲波变换和压缩感知理论的地震数据重建[J]. 中国石油大学学报(自然科学版),41(5):61–68. doi: 10.3969/j.issn.1673-5005.2017.05.007 Cao J J,Wang S X,Li W B. 2017. Seismic reconstruction with 3D low-redundancy curvelet transform and compressed sensing theory[J]. Journal of China University of Petroleum (Edition of Natural Science),41(5):61–68 (in Chinese).
曹静杰,杨志权,杨歧焱. 2020. 一种基于压缩感知的地震数据重建方法及其在城市活断层地震勘探中的应用[J]. 地球物理学进展,35(4):1545–1551. doi: 10.6038/pg2020DD0267 Cao J J,Yang Z Q,Yang Q Y. 2020. Compressive sensing based seismic reconstruction method and its application to seismic exploration of urban active faults[J]. Progress in Geophysics,35(4):1545–1551 (in Chinese).
付明柏. 2013. 基于异质矩阵完全的缺失数据恢复混合集成算法[J]. 云南师范大学学报(自然科学版),33(6):67–72. Fu M B. 2013. Mixed ensemble heterogeneous matrix completion for missing value estimation[J]. Journal of Yunnan Normal University (Natural Sciences Edition),33(6):67–72 (in Chinese).
孔德辉. 2017. 基于压缩感知的地震数据重建及若干问题研究[D]. 成都:电子科技大学:1–11. Kong D H. 2017. Research on Some Issues of Seismic Data Reconstruction Based on Compressed Sensing[D]. Chengdu:University of Electronic Science and Technology of China:1–11 (in Chinese).
赵杨. 2018. 地震体波走时与重力联合反演研究及在南北地震带南段的应用[D]. 北京:中国地质大学(北京):1–9. Zhao Y. 2018. Joint Inversion of Seismic Traveltime and Gravity Data and Its Application in Imaging Crustal Structure Around Southern Section of North-South Earthquake Belt[D]. Beijing:China University of Geosciences (Beijing):1–9 (in Chinese).
郑雪辰. 2019. 基于压缩感知理论和SPGL1算法的地震数据重建[D]. 西安:长安大学:1–9. Zheng X C. 2019. Seismic Data Reconstruction Based on Compressive Sensing and SPGL1 Algorithm[D]. Xi’an:Chang’an University:1–9 (in Chinese).
Bai L S,Lu H Y,Liu Y K. 2020. High-efficiency observations:Compressive sensing and recovery of seismic waveform data[J]. Pure Appl Geophys,177(1):469–485. doi: 10.1007/s00024-018-2070-z
Candès E,Demanet L,Donoho D,Ying L X. 2006a. Fast discrete curvelet transforms[J]. Multiscale Model Simul,5(3):861–899. doi: 10.1137/05064182X
Candès E J,Romberg J,Tao T. 2006b. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inform Theory,52(2):489–509. doi: 10.1109/TIT.2005.862083
Cao J J,Wang Y F,Wang B F. 2015. Accelerating seismic interpolation with a gradient projection method based on tight frame property of curvelet[J]. Explor Geophys,46(3):253–260. doi: 10.1071/EG14016
Daubechies I,Defrise M,De Mol C. 2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Commun Pure Appl Math,57(11):1413–1457. doi: 10.1002/cpa.20042
Donoho D L. 2006. Compressed sensing[J]. IEEE Trans Inform Theory,52(4):1289–1306. doi: 10.1109/TIT.2006.871582
Herrmann F J,Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames[J]. Geophys J Int,173(1):233–248. doi: 10.1111/j.1365-246X.2007.03698.x
Ismael V R,Mauricio S,Yu J G. 2012. A compressive sensing framework for seismic source parameter estimation[J]. Geophys J Int,191(3):1226–1236
Rawlinson N,Pozgay S,Fishwick S. 2010. Seismic tomography:A window into deep Earth[J]. Phys Earth Planet Inter,178(3/4):101–135.
Wang B,Chen X,Li J,Cao J. 2016. An improved weighted projection onto convex sets methods for seismic data interpolation and denoising[J]. IEEE J STARS,9:228–235.
Wang R J. 1999. A simple orthonormalization method for stable and efficient computation of Green’s functions[J]. Bull Seismol Soc Am,89(3):733–741. doi: 10.1785/BSSA0890030733
Zhang H L,Song S,Liu T Y. 2007. The ridgelet transform with non-linear threshold for seismic noise attenuation in marine carbonates[J]. Appl Geophys,4(4):271–275. doi: 10.1007/s11770-007-0027-6
Zhou Q B,Gao J H,Wang Z G. 2015. Sparse spike deconvolution of seismic data using trust-region based SQP algorithm[J]. J Comput Acoust,23(4):1540002. doi: 10.1142/S0218396X15400020




 下载:
下载: