An automatic S phase picking algorithm for local earthquake events
-
摘要: 基于特征值分解方法，本文讨论了一种适用于地方震事件S波震相到时拾取的自动处理算法。该算法计算参数少、简便快捷、易于实现，通过选用七个不同长度的时间窗，有效地减小了窗长选择不合理所引起的震相拾取误差。利用福建地震台网记录的9 855条三分向波形记录进行测试，结果表明：本文方法的S波平均拾取偏差为（0.003±1.34） s，其中79.6%的记录拾取偏差小于0.5 s，4.1%的记录拾取偏差超过2.0 s，说明本文方法能够满足日常工作基本需求。综上分析认为，波形记录质量是影响拾取算法结果精度的最主要因素，信噪比较高的记录，其S波到时拾取偏差显著优于信噪比较低的记录，对信噪比较低的部分记录进行带通滤波预处理后，S波震相拾取精度也有所提升。Abstract: Base on eigenvalue decomposition calculation, we discussed an automatic S phase picking algorithm suitable for local earthquake events. The algorithm needs few parameters, less computer resources and is easy to realize. By choosing seven time windows with different time length, it effectively reduce the S phase pick errors that caused by unreasonable time window selection. By taking 9 855 three-component records of Fujian seismic monitoring network, we test the applicability and accuracy of this algorithm. The results show that average S phase picking error by this method is （0.003±1.34） s, 79.6% of them are within 0.5 s, 4.1% of them are greater than 2.0 s, which indicates that the algorithm can meet the demands for daily S phase picking. All above-mentioned suggests that the quality of records is the most important factor that affects the accuracy of picking results, the S phase picking errors for high signal-noise ratio records are usually smaller than those for low signal-noise ratio records, and the accuracy of S phase picking for some low signal-noise ratio records will be improved after a band-pass filter preprocess.
-
Keywords:
- eigenvalue decomposition /
- S wave /
- seismic phase detection /
- real-time process /
- signal-noise ratio
-
引言
随着我国地震观测台站数量的不断增加，区域地震监测能力的逐渐增强，可监测震级的下限不断降低。密集地震观测台网产出高质量地震观测数据的同时，也对现有业务系统提出了更多的新需求，其中从实时产出的地震观测数据中准确判别和拾取不同类型的震相是最基础的、最迫切的需求之一。这些震相信息为更好地认识地壳介质结构、了解发震断层、获取震源信息、进行地震预警服务等提供数据支持。
为了更快更准确地从连续地震记录波形中判别和拾取出地震震相，许多学者都开展了系列研究，并提出了很多实用的算法。这些震相拾取算法可归纳为能量准则（Allen，1982；Baer，Kradolfer，1987；Lomax et al，2012；马强等，2013）、极化分析（Vidale，1986；Ruud，Husebye，1992；Amoroso et al，2012）、模糊分析（Chu，Mendel，1994）、人工神经网络（Dai，MacBeth，1995）、高阶统计量（Saragiotis et al，2002；Küperkoch et al，2012）、小波变换（Anant，Dowla，1997；刘希强等，1998，2000）及基于机器学习（Kong et al，2019；Perol et al，2018；Ross et al，2018a，b；Zhu et al，2018；李安等，2020）等几大类相关算法。
相较于初动清晰、信噪比较高的P波震相，S波震相由于受到P波尾波和（或）其它转换波震相的干扰，信噪比通常较P波要低得多，因此S波震相拾取结果的准确性普遍低于P波震相。即使是有经验的分析人员，仍无法保证S波震相拾取的准确性。现有的S波震相自动拾取算法大都是基于极化特征分析的方法（Flinn，1965；Vidale，1986；Jurkevics，1988；Cichowicz，1993），这些算法利用三分向地震波形记录，基于P波震相与S波震相的不同偏振特征，通过计算质点运动的偏振度、线性度等参数，寻找特征函数突变发生的点，进而判定S波震相到时的位置。此类方法大都适用于单台记录，算法有效性依赖于其有效剥离多种震相的能力，如将剪切波与面波分离等。Lois等（2013）即利用一个基于特征值分析的特征函数，提出了一种S波自动拾取时域算法，该算法对于P波、S波的极化方向不作任何假设，是一种近乎“零参数”的时域实时算法。本文则在该算法的基础上，进一步优化相关参数，并利用福建地震台网2015—2018年期间的9 855条三分向波形记录分析进行验证。
1. 方法
在实时地震数据处理中，通常采用滑动窗的方式将连续观测数据离散为固定长度的数据，而后再采用相应离线数据处理算法进行分析。同样，对于一段已知P波到时位置的波形记录，本文在P波到时后采用滑动窗将记录划分，并根据一定的滑动步长进行滑动处理，然后对各小窗的三分向波形记录求取特征值，进而可获得特征值时程，本文将该特征值时程作为S波识别特征函数。其中，由三分向波形求取特征值可采用数学分析中协方差矩阵分解的方式得到，特征值时程的物理含义是确定质点运动偏振方向。假定由三分向波形数据计算得到的协方差矩阵为
$${\boldsymbol{C}} {\text{＝}} \left[ {\begin{array}{*{20}{c}} {{\rm{cov}} {\text{（}}x{\text{，}}x{\text{）}}}&{{\rm{cov}} {\text{（}}x{\text{，}}y{\text{）}}}&{{\rm{cov}} {\text{（}}x{\text{，}}z{\text{）}}} \\ {{\rm{cov}} {\text{（}}y{\text{，}}x{\text{）}}}&{{\rm{cov}} {\text{（}}y{\text{，}}y{\text{）}}}&{{\rm{cov}} {\text{（}}y{\text{，}}z{\text{）}}} \\ {{\rm{cov}} {\text{（}}z{\text{，}}x{\text{）}}}&{{\rm{cov}} {\text{（}}z{\text{，}}y{\text{）}}}&{{\rm{cov}} {\text{（}}z{\text{，}}z{\text{）}}} \end{array}} \right]{\text{，}}$$ (1) 式中，
${\rm{cov}} {\text{（}}x{\text{，}}y{\text{）}} = \Big[\sum\limits_{i {\text{＝}} 1}^L {{\text{（}}{x_i} {\text{－}} \overline x{\text{）}}{\text{（}}{y_i} {\text{－}} \overline y{\text{）}}}\Big]\Big/ L$ ，L为滑动窗长度，且${\rm{cov}} {\text{（}}x{\text{，}}y{\text{）}} {\text{＝}} {\rm{cov}} {\text{（}}y{\text{，}}x{\text{）}}$ ，${\rm{cov}} {\text{（}}x{\text{，}}z{\text{）}} {\text{＝}} $ $ {\rm{cov}} {\text{（}}z{\text{，}}x{\text{）}}$ ，${\rm{cov}} {\text{（}}y{\text{，}}z{\text{）}} {\text{＝}} {\rm{cov}} {\text{（}}z{\text{，}}y{\text{）}}$ 。将式（1）分解即可分别得到三个特征值${\lambda _1}{\text{，}}{\lambda _2}{\text{，}}{\lambda _3}$ （${\lambda _1} {\text{＞}} {\lambda _2} {\text{＞}} {\lambda _3}$ ）及相应的三个特征向量${ {\boldsymbol{u}}_{{1}}}{\text{，}}{ {\boldsymbol{u}}_{{2}}}{\text{，}}{ {\boldsymbol{u}}_{{3}}}$ 。对于连续波形记录，即可得到特征值时程${\lambda _1}{\text{（}}t{\text{）}}{\text{，}}{\lambda _2}{\text{（}}t{\text{）}}{\text{，}} $ $ {\lambda _3}{\text{（}}t{\text{）}}$ 。据此也可分别计算得到信号偏振线性度、质点运动平面度、P波传播方位角、线性运动入射角等参数（Jurkevics，1988；马强，2008）。由于
${\lambda _1}{\text{（}}t{\text{）}}$ 对信号传播方向上的能量突变更为敏感（图1d），因此本文仅选择其作为特征函数。为了更好地体现信号中能量的微弱变化并突显信号突变位置，本文求取${\lambda _1}{\text{（}}t{\text{）}}$ 的平方根$f{\text{（}}t{\text{）}} {\text{＝}} \sqrt {{\lambda _1}{\text{（}}t{\text{）}}}$ （图1e），放大${\lambda _1}{\text{（}}t{\text{）}}$ 中低值成分的同时压低${\lambda _1}{\text{（}}t{\text{）}}$ 中高值成分进而减小其动态范围，实现对特征函数的压缩。尤其对于信噪比较低的事件波形，采用此方式的特征函数凸显信号中的能量突变位置更为有效。随后，选取P波初至到S尾波段对$f{\text{（}}t{\text{）}}$ 求取峰度系数$K{\text{（}}t{\text{）}} {\text{＝}} $ $ kur[f{\text{（}}t{\text{）}}]$ ，即可从特征函数中将S波到时位置进一步凸显出来（图1f）。应用该时间窗是为了避免将后续事件的初至震相错误识别为本次事件S波震相，但对于密集事件序列，该时间窗的选取比较困难。由图1f可见，在S波到时附近$K{\text{（}}t{\text{）}}$ 呈现一个显著的陡坎，但S波到时点位于陡坎起始最低处，因此在实际应用中很难准确拾取，需要进一步处理，即对$K{\text{（}}t{\text{）}}$ 求取一阶差分$\Delta K{\text{（}}t{\text{）}}$ ，此时S波到时与$\Delta K{\text{（}}t{\text{）}}$ 峰值位置相一致，S波到时位置将更容易判别，据此即可对S波粗到时进行拾取。最后，应用自回归赤池信息准则（Akaike information criteria，缩写为AIC）（Akaike，1974）在所拾取S波粗到时位置附近精确判别（前后各取0.3 s），即可获得准确可靠的S波到时信息。![]()
图 1 本文S波拾取方法算例示意图事件发震时刻为2015-01-02 00:33:56.89，震中距为3.8 km的GTSK台站记录，窗长为0.2 s。图（a−c）为三分向波形记录；图（d）为特征值时程；图（e）为特征函数f （t）；图（f）为峰度系数时程K（t）；图（g）为求取差分后特征函数ΔK（t）Figure 1. An example of S phase picking by using the algorithm of this studyThe origin time of the event is 00:33:56.89 on 2 January 2015. The wavforms were recorded by the station GTSK with epicentral distance 3.8 km，and window length is taken as 0.2 s. Figs. （a） to （c） are three-component seismic records；Fig. （d） shows the history of three eigenvalues；Fig. （e） is the characteristic function f （t）；Fig. （f） shows time history of Kurtosis coefficient K（t），and Fig. （g） shows the differential characteristic function ΔK（t）滑动时窗长度是本文算法中需要确定的重要参数。若选择较短的时窗，该算法对于特征函数中微小的改变过于敏感，拾取到的S波到时位置将超前；若选择过长的时窗，算法将缺乏必要的敏感度，拾取到的S波到时位置将显著滞后。实时地震数据处理中，算法的鲁棒性是一个重要的指标，选择某一固定时间窗长度显然无法满足所有事件的需求。为此，本文采用多窗口综合加权方法，窗口长度为0.2—1.4 s，间隔0.2 s，共7个。首先在各窗口中拾取S波到时Si，并计算S震相信噪比Ri，然后依据信噪比综合加权给出S波到时位置，即
$${S_{\rm{f}}} {\text{＝}} \dfrac{{\displaystyle\sum\limits_{i {\text{＝}} 1}^7 {{S_i}{R_i}} }}{{\displaystyle\sum\limits_{i {\text{＝}} 1}^7 {{R_i}} }}{\text{.}}$$ (2) 2. 数据
本文研究中收集了福建台网2015—2018年记录的1 862次地方震事件，震级范围为ML−0.5—4.2，仅挑选其中震中距小于100 km的9 855条三分向地震动记录计算分析，在此震中距范围内，初至S波震相均为Sg。本文以人工地震编目提供的Sg震相拾取结果为参考，对比采用本文方法的拾取震相到时拾取位置，以验证本文算法的准确性及实用性。本研究中使用的台站观测记录以仙游震群和台湾海峡南部震群为主，这两个震群的观测数据量约占所有分析记录1/3左右，各台站记录数量空间分布如图2所示。本文所用台站记录在震中距100 km内基本呈均匀分布，震中距分布如图3所示。
![]()
图 2 本文所用台站记录随震中距和震级分布Figure 2. Epicentral distance and magnitude distribution for earthquake records used in this study3. 结果与讨论
应用本文方法得到的S波到时拾取结果与人工编目S震相拾取结果间的偏差统计情况如图4所示。结果显示，相较于人工拾取结果，本文方法的S波震相到时拾取平均偏差为（−0.003±1.34） s，其中拾取偏差小于0.2 s的记录所占比例为63.9%，拾取偏差小于0.5 s的记录所占比例为79.6%，即应用本文方法能够较准确地对大部分S波震相到时进行拾取。但从图3中也可以明显看出，应用本文方法的S波震相到时拾取结果有超前于人工拾取结果的趋势，因而造成图4b中统计直方图的偏态分布。本文将测试数据进一步划分为仙游震群、台湾海峡震群及其它事件三类，每类分别包括1 276条、2 330条和6 249条记录，并分析不同类别的S波到时拾取结果精度，结果如图5所示。由该图可见，不同的类别事件应用本文方法的S波拾取结果偏差分布较为一致，均表现出超前于人工拾取结果的趋势，三类事件的S波拾取偏差分别为（−0.018±1.68） s，（−0.053±1.56） s和（0.011±1.17） s。综上可见，本文所研究的相关算法具有较好的适用性，应用于不同区域的事件时均表现稳定。
![]()
图 4 应用本文方法的S波震相到时拾取偏差统计图（a）为各记录S震相拾取偏差散点图，图（b）和（c）为S震相拾取偏差统计直方图Figure 4. Statistics of S phase arrival time pick errors by using our methodFig. （a） gives S phase picking error for each record，Figs. （b） and （c） show the histogram of the phase picking error![]()
图 5 分区域S波震相到时拾取偏差结果统计（a） 仙游震群；（b） 台湾海峡南部震群；（c） 其它事件Figure 5. Statistics of S phase arrival time picking error in different regions（a） Xianyou sequence；（b） Southern Taiwan Strait sequence；（c） Other events此外，由图4还可以看出，仍有约11.2%的记录的S波震相到时拾取偏差超过±1.0 s，其中约4.1%的记录的S波震相到时拾取偏差超过±2.0 s，图6分别列举出三个拾取偏差较大的记录情况。进一步分析后，可将引起拾取偏差过大的原因归纳为三个方面。首先，信噪比较低是造成S波震相拾取偏差较大的显著原因。如图6a中所示波形记录，由于S波震相受到前序P波尾波的污染，信噪比较低，即使对于有经验的分析人员仍较难准确拾取，这也是通用S波震相到时拾取算法准确度不高的主要困难所在。本文采用式（3）截取人工拾取S波到时前后各2 s窗长内的波形记录并计算均方根进而得到各记录的信噪比，对于采样率为100 的记录：
![]()
图 6 S波震相到时拾取偏差较大的波形记录（a） 低信噪比记录结果；（b） 图（a）中记录1—20 Hz带通滤波后的结果；（c） 多事件叠加记录结果；（d） EW向异常记录结果Figure 6. Waveforms with large S phase arrival time picking error（a） The result for a low SNR record；（b） The result for the record in Fig. （a） after 1−20 Hz band-pass filtering；（c） The result for a multi-event record；（d） The result for an abnormal record in EW component$${\rm{SNR}} {\text{＝}} {\dfrac{{\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i {\text{＝}} s}^{s {\text{＋}} n} {{x_i}} } } }{ {\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i {\text{＝}} s {\text{－}} n}^s {{x_i}} } }}}{\text{，}}$$ (3) 式中s为人工拾取S波到时位置，n为数据长度（取200）.
随后，对406条S波到时拾取偏差超过±2.0 s的记录的信噪比进行统计，并与其它记录的信噪比情况进行对比，如图7所示。可以直观地看出低信噪比（＜2.0）记录在拾取偏差超过±2.0 s的记录中占有最大比例（图7a），与之相应，对于其余拾取误差较小的记录，高信噪比记录所占的比例较高（图7b）。图7以信噪比2.0为界，分别给出了低信噪比和高信噪比情况下S波震相拾取误差分布情况。由该结果可见：对于低信噪比波形记录，S波震相拾取误差超过1.0 s的比例为19%，显著多于高信噪比波形记录中的比例（9%）；且高信噪比波形记录中S波震相拾取误差小于0.2 s的比例（70%）更明显高于低信噪比波形记录中的比例（52%）。由此，作者认为观测记录信噪比是显著影响S波震相拾取精度的最重要因素。表1分别列出了针对不同信噪比记录，应用本文方法统计得到的S波震相拾取精度结果。可见，随着记录信噪比的提高，S波拾取残差呈平均值减小、标准差降低的趋势，与图7、图8所示结果一致。此外，从应用本文方法拾取的S－P到时差与人工拾取S－P到时差的对比（图9a）中也可以看出，偏差较大（如＞±2.0 s）记录的信噪比大多较低，而且随着震中距增加（S－P到时差增大），S波拾取结果的偏差分布也随之更为离散，显然这也与记录信噪比逐渐降低有关。同时，本文也对比了不同震群事件的S波拾取精度（图9b-d），本文算法在不同震群中的表现也较为一致，其中：仙游震群（图9b）中震中距较小的记录占比较高，算法对于此部分记录（＜5.0 s）也显示了更佳的性能，显然其信噪比也更高；同理海峡震群（图9c）和其它事件（图9d）中大震中距记录占比也相对更高，S波拾取残差随信噪比降低也变得更为离散，再次说明了记录的信噪比在应用本文S波拾取算法中的重要性。
![]()
图 7 地震记录信噪比的分布（a） 拾取偏差大于2.0 s的406条记录；（b） 拾取偏差小于2.0 s的9449条记录Figure 7. SNR distribution of seismic records（a） 406 records with S phase picking errors larger than ±2.0 s；（b） 9449 records with S phase picking errors less than ±2.0 s表 1 不同信噪比记录的S波到时拾取偏差统计Table 1. Statistic on S phase picking error for different SNR recordsSNR 记录数量 偏差均值/s 偏差中值/s 偏差标准差/s ＜2 2 953 0.135 0.040 1.92 2—5 6 416 −0.051 0.050 0.99 ≥5 486 −0.202 0.040 0.96 ![]()
图 8 不同信噪比记录S波震相拾取偏差分布（a） 信噪比小于2.0的记录；（b） 信噪比大于2.0的记录Figure 8. Pi chart of S phase detection error for different SNR records（a） Records with SNR less than 2.0；（b） Records with SNR larger than 2.0![]()
图 9 应用本文方法所得的S－P到时差与人工拾取结果对比及其信噪比分布（a） 所有记录；（b） 仙游震群；（c） 台湾海峡震群；（d） 其它事件Figure 9. Comparison of the arrival time differences for S−P by our method with those by manual picking and SNR distributions（a） All records；（b） Xianyou sequence；（c） Taiwan Strait sequence；（d） Other events若对事件波形进行带通滤波（如1—20 Hz），则可在一定程度上提高记录质量，也将有利于提高S波震相的拾取精度。图6b展示了图6a所示波形记录经1—20 Hz零相移带通滤波后再次应用本文方法的S波震相拾取结果。图10则分别为该记录滤波前后应用本文方法的具体识别效果，其中各子图所展示内容与图1一致。如前文已提及，不同滑动窗长下，S波到时拾取位置也会有所差异，因而本文采用式（2）对不同窗长下的S波到到时拾取位置进行加权综合，而图1和图10仅为某一窗长（分别为0.2 s和1.0 s）下的拾取结果，与图6中所示S波到时综合加权判别结果（虚线）会有所差异。对比可见，由于波形记录质量显著提高，S波震相拾取也更为准确，相较于人工拾取结果的偏差仅为0.36 s。需要说明的是，本文图4中所示震相拾取偏差均基于原始波形，未经带通滤波。鉴于上述分析，可推测出，若能够通过带通滤波提高部分低信噪比记录的信噪比水平，则震相拾取的偏差将得以改善。作者也将收集相关资料，继续深化该部分的研究。
![]()
图 10 图6a中信噪比较低记录带通滤波前（a）、后（b）的S波到时拾取各子图意思同图1，事件发震时间为2015-01-08 05:48:44.56，台站ZPCH的震中距为99.8 km，窗长为1.0 sFigure 10. S phase picking for a low SNR record in Fig. 6a before （a） and after （b） band-pass filteringEach subfigure has the same meaning as Fig. 1. The event occurred at 05:48:44.56 on 8 January 2015，which was recorded by the station ZPCH with epicentral distance 99.8 km. And time window length is taken as 1.0 s针对地震序列（尤其是大震后的密集余震序列）的处理能力也是考验震相拾取算法实用性的一个重要指标。鉴于序列震事件记录的复杂性及多样性，现有常规处理算法（如STA/LTA，AR-AIC，Z-detect等）均不能较为有效地处理和应对，本研究所涉及相关算法本质上也属于这类算法范畴。如前文所述，该算法不仅依赖于P波到时位置，而且仅能在P波到时之后的一段时间窗内识别唯一一个S波到时位置。显然，该算法基本不具备处理更为复杂的情况下序列地震的能力。图6c展示了一个密集序列的波形记录，在30 s内记录了多个小震事件，由于记录过于复杂，人工分析也仅标注了其中主要的S波震相到时（图6c中所标识Sg震相），而本文方法则只拾取到了序列中的一个可能的S波震相。由于本文方法尚不具备连续拾取后续震相的功能，因此本文方法在此类序列地震记录中的处理结果欠佳。在实际业务系统应用中，可适当提高S波尾波段阈值（即缩短事件持续时间），部分程度上可弥补在序列事件处理中的不足。
此外，由于波形记录本身存在的质量缺陷也是造成S波震相拾取偏差过大的显著影响因素。本文中所讨论相关算法的有效性和可靠性均依赖特征值分析结果，而一旦所分析的波形存在异常，则将直接影响特征值的分解结果，进而造成S波到时拾取结果的较大偏差。由图6d可见，由于EW向分量波形显著异常（该分向无输出），特征值计算错误，最终导致S波拾取结果出现较大偏差。尽管此类问题在实际业务应用中无法完全避免，但通过对记录波形质量的分析监控，能够有效地避免将异常波形纳入处理，从而提高S波到时拾取结果的准确性。
4. 结论
本文基于特征值分解算法，研究了一种可用于地方震S波震相实时提取的实用化算法。该算法对P、S波偏振方向不作任何假设，通过应用多个滑动时间窗即可较准确地拾取出S波震相到时，避免由于窗口长度选择不合理而造成的拾取偏差，满足地震信号的实时处理需求。应用福建地震台网地震观测的数据测试结果表明，该算法S波震相拾取精度高，适用于实时地震信息处理系统，但尚不具备密集序列连续处理能力。此外，由于应用该算法前需要首先已知P波到时信息，因此S波震相到时拾取的可靠性一定程度上也依赖于P波震相到时拾取的准确程度。但相较于S波震相，P波震相初动更为明显，因而更易于拾取，拾取精度更有保障。本文仅以福建地震台网100 km范围内的地方震事件为主，所拾取震相也主要为Sg震相，重点对该算法的适用性展开分析讨论，因而所得相关结论也可能不够全面。作者将继续收集相关波形数据，以更充分地论证该算法的适用性及其在实际数据处理系统中应用的可靠性。
随着地震观测台站数量的不断增加及观测数据质量的逐步提升，近年来深度学习等人工智能算法在地震数据处理领域内的应用也越来越多。尤其是在震相拾取方面，已经有多个学者提出了高性能、高可信的相关震相拾取算法，如GPD算法（Ross et al，2018a）、U-net算法（赵明等，2019）、PhaseNet算法（Zhu，Beroza，2018）等。作者也将应用这类算法开展相关研究，并将其与传统方法进行整合，以期更快、更准、更全地产出震相到时信息。
审稿专家为本文提出了建设性的修改意见，作者在此表示感谢。
-
![]()
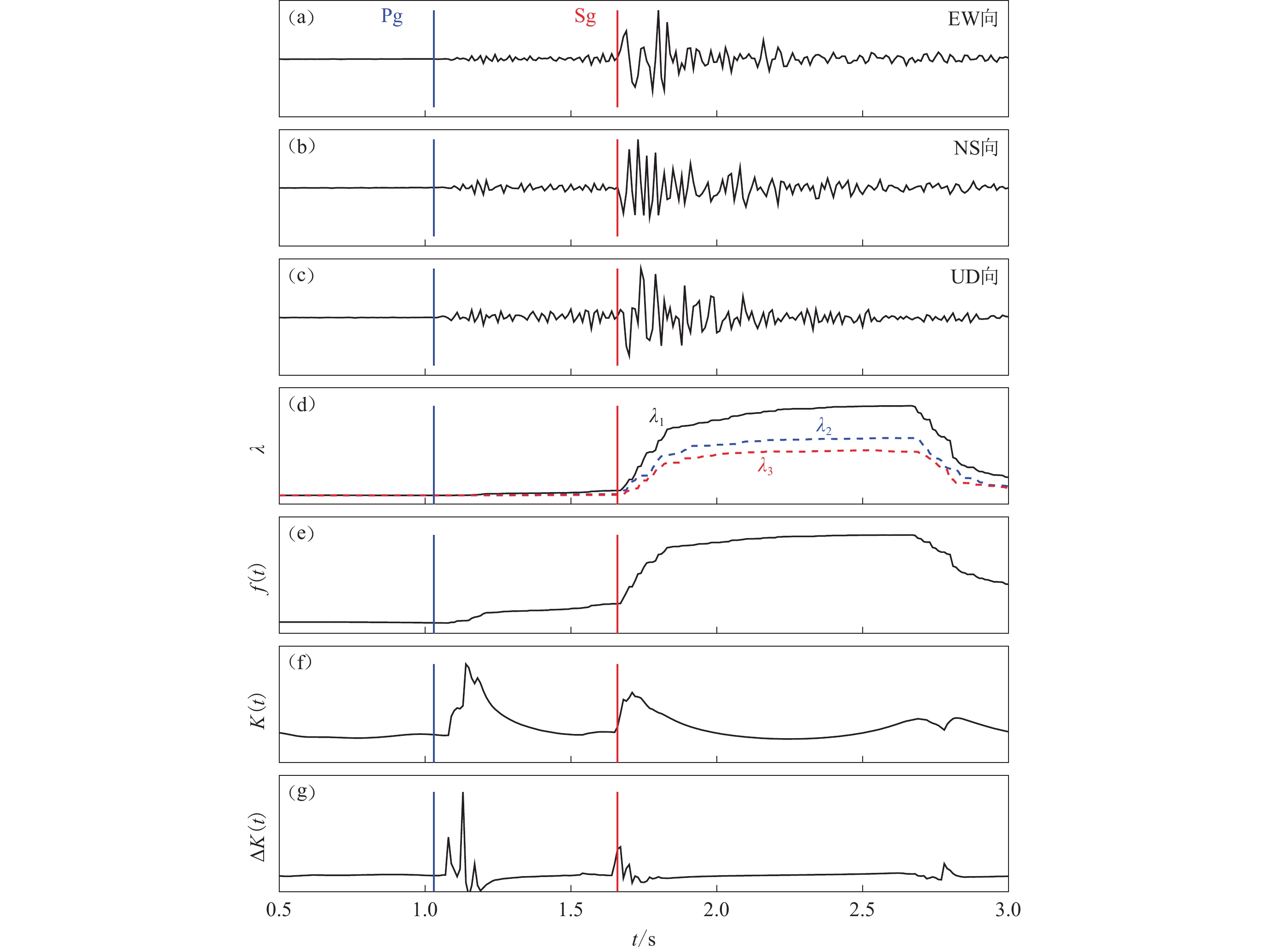
图 1 本文S波拾取方法算例示意图
事件发震时刻为2015-01-02 00:33:56.89，震中距为3.8 km的GTSK台站记录，窗长为0.2 s。图（a−c）为三分向波形记录；图（d）为特征值时程；图（e）为特征函数f （t）；图（f）为峰度系数时程K（t）；图（g）为求取差分后特征函数ΔK（t）
Figure 1. An example of S phase picking by using the algorithm of this study
The origin time of the event is 00:33:56.89 on 2 January 2015. The wavforms were recorded by the station GTSK with epicentral distance 3.8 km，and window length is taken as 0.2 s. Figs. （a） to （c） are three-component seismic records；Fig. （d） shows the history of three eigenvalues；Fig. （e） is the characteristic function f （t）；Fig. （f） shows time history of Kurtosis coefficient K（t），and Fig. （g） shows the differential characteristic function ΔK（t）
![]()
图 2 本文所用台站记录随震中距和震级分布
Figure 2. Epicentral distance and magnitude distribution for earthquake records used in this study
![]()
图 4 应用本文方法的S波震相到时拾取偏差统计
图（a）为各记录S震相拾取偏差散点图，图（b）和（c）为S震相拾取偏差统计直方图
Figure 4. Statistics of S phase arrival time pick errors by using our method
Fig. （a） gives S phase picking error for each record，Figs. （b） and （c） show the histogram of the phase picking error
![]()
图 5 分区域S波震相到时拾取偏差结果统计
（a） 仙游震群；（b） 台湾海峡南部震群；（c） 其它事件
Figure 5. Statistics of S phase arrival time picking error in different regions
（a） Xianyou sequence；（b） Southern Taiwan Strait sequence；（c） Other events
![]()
图 6 S波震相到时拾取偏差较大的波形记录
（a） 低信噪比记录结果；（b） 图（a）中记录1—20 Hz带通滤波后的结果；（c） 多事件叠加记录结果；（d） EW向异常记录结果
Figure 6. Waveforms with large S phase arrival time picking error
（a） The result for a low SNR record；（b） The result for the record in Fig. （a） after 1−20 Hz band-pass filtering；（c） The result for a multi-event record；（d） The result for an abnormal record in EW component
![]()
图 7 地震记录信噪比的分布
（a） 拾取偏差大于2.0 s的406条记录；（b） 拾取偏差小于2.0 s的9449条记录
Figure 7. SNR distribution of seismic records
（a） 406 records with S phase picking errors larger than ±2.0 s；（b） 9449 records with S phase picking errors less than ±2.0 s
![]()
图 8 不同信噪比记录S波震相拾取偏差分布
（a） 信噪比小于2.0的记录；（b） 信噪比大于2.0的记录
Figure 8. Pi chart of S phase detection error for different SNR records
（a） Records with SNR less than 2.0；（b） Records with SNR larger than 2.0
![]()
图 9 应用本文方法所得的S－P到时差与人工拾取结果对比及其信噪比分布
（a） 所有记录；（b） 仙游震群；（c） 台湾海峡震群；（d） 其它事件
Figure 9. Comparison of the arrival time differences for S−P by our method with those by manual picking and SNR distributions
（a） All records；（b） Xianyou sequence；（c） Taiwan Strait sequence；（d） Other events
![]()
图 10 图6a中信噪比较低记录带通滤波前（a）、后（b）的S波到时拾取
各子图意思同图1，事件发震时间为2015-01-08 05:48:44.56，台站ZPCH的震中距为99.8 km，窗长为1.0 s
Figure 10. S phase picking for a low SNR record in Fig. 6a before （a） and after （b） band-pass filtering
Each subfigure has the same meaning as Fig. 1. The event occurred at 05:48:44.56 on 8 January 2015，which was recorded by the station ZPCH with epicentral distance 99.8 km. And time window length is taken as 1.0 s
表 1 不同信噪比记录的S波到时拾取偏差统计
Table 1 Statistic on S phase picking error for different SNR records
SNR 记录数量 偏差均值/s 偏差中值/s 偏差标准差/s ＜2 2 953 0.135 0.040 1.92 2—5 6 416 −0.051 0.050 0.99 ≥5 486 −0.202 0.040 0.96 
下载: 导出CSV
-
李安,杨建思,彭朝勇,郑钰,刘莎. 2020. 基于样本增强的卷积神经网络震相拾取方法[J]. 地震学报,42(2):163–176. doi: 10.11939/jass.20190070 Li A,Yang J S,Peng C Y,Zheng Y,Liu S. 2020. Seismic phase identification using the convolutional neural networks based on sample enhancement[J]. Acta Seismologica Sinica,42(2):163–176 (in Chinese). doi: 10.11939/jass.20190070（inChinese）
刘希强,周蕙兰,郑治真,沈萍,杨选辉,马延路. 1998. 基于小波包变换的弱震相识别方法[J]. 地震学报,20(4):373–380. doi: 10.3321/j.issn:0253-3782.1998.04.005 Liu X Q,Zhou H L,Zheng Z Z,Shen P,Yang X H,Ma Y L. 1998. Identification method of weak seismic phases on the basis of wavelet packet transform[J]. Acta Seismologica Sinica,20(4):373–380 (in Chinese).
刘希强,周蕙兰,沈萍,杨选辉,马延路,李红. 2000. 用于三分向记录震相识别的小波变换方法[J]. 地震学报,22(2):125–131. doi: 10.3321/j.issn:0253-3782.2000.02.002 Liu X Q,Zhou H L,Shen P,Yang X H,Ma Y L,Li H. 2000. Identification method of seismic phase in three-component seismograms on the basis of wavelet transform[J]. Acta Seismologica Sinica,22(2):125–131 (in Chinese).
马强. 2008. 地震预警技术研究及应用[D]. 哈尔滨: 中国地震局工程力学研究所: 14–39. Ma Q. 2008. Study and Application on Earthquake Early Warning[D]. Harbin: China Earthquake Administration, Institute of Engineering Mechanics: 14–39 （in Chinese）. 马强,金星,李山有,陈绯雯,廖诗荣,韦永祥. 2013. 用于地震预警的P波震相到时自动拾取[J]. 地球物理学报,56(7):2313–2321. doi: 10.6038/cjg20130718 Ma Q,Jin X,Li S Y,Chen F W,Liao S R,Wei Y X. 2013. Automatic P-arrival detection for earthquake early warning[J]. Chinese Journal of Geophysics,56(7):2313–2321 (in Chinese). doi: 10.6038/cjg20130718（inChinese）
赵明,陈石,房立华,Yuen D A. 2019. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报,62(8):3034–3042. doi: 10.6038/cjg2019M0495 Zhao M,Chen S,Fang L H,Yuen D A. 2019. Earthquake phase arrival auto-picking based on U-shaped convolutional neural network[J]. Chinese Journal of Geophysics,62(8):3034–3042 (in Chinese).
Akaike H. 1974. A new look at the statistical model identification[J]. IEEE Trans Automat Control,19(6):716–723. doi: 10.1109/TAC.1974.1100705
Allen R. 1982. Automatic phase pickers:Their present use and future prospects[J]. Bull Seismol Soc Am,72(6B):S225–S242. doi: 10.1785/BSSA07206B0225
Amoroso O,Maercklin N,Zollo A. 2012. S-wave identification by polarization filtering and waveform coherence analyses[J]. Bull Seismol Soc Am,102(2):854–861. doi: 10.1785/0120110140
Anant K S,Dowla F U. 1997. Wavelet transform methods for phase identification in three-component seismograms[J]. Bull Seismol Soc Am,87(6):1598–1612.
Baer M,Kradolfer U. 1987. An automatic phase picker for local and teleseismic events[J]. Bull Seismol Soc Am,77(4):1437–1445. doi: 10.1785/BSSA0770041437
Chu C K P,Mendel J M. 1994. First break refraction event picking using fuzzy logic systems[J]. IEEE Trans Fuzzy Syst,2(4):255–266. doi: 10.1109/91.324805
Cichowicz A. 1993. An automatic S-phase picker[J]. Bull Seismol Soc Am,83(1):180–189.
Dai H C,MacBeth C. 1995. Automatic picking of seismic arrivals in local earthquake data using an artificial neural network[J]. Geophys J Int,120(3):758–774. doi: 10.1111/j.1365-246X.1995.tb01851.x
Flinn E A. 1965. Signal analysis using rectilinearity and direction of particle motion[J]. Proc IEEE,53(12):1874–1876. doi: 10.1109/PROC.1965.4462
Jurkevics A. 1988. Polarization analysis of three-component array data[J]. Bull Seismol Soc Am,78(5):1725–1743.
Küperkoch L,Meier T,Brüstle A,Lee J,Friederich W. 2012. Automated determination of S-phase arrival times using autoregressive prediction:Application to local and regional distances[J]. Geophys J Int,188(2):687–702. doi: 10.1111/j.1365-246X.2011.05292.x
Kong Q K,Trugman D T,Ross Z E,Bianco M J,Meade B J,Gerstoft P. 2019. Machine learning in seismology:Turning data into insights[J]. Seismol Res Lett,90(1):3–14. doi: 10.1785/0220180259
Lois A,Sokos E,Martakis N,Paraskevopoulos P,Tselentis G A. 2013. A new automatic S-onset detection technique:Application in local earthquake data[J]. Geophysics,78(1):KS1–KS11. doi: 10.1190/GEO2012-0050.1
Lomax A,Satriano C,Vassallo M. 2012. Automatic picker developments and optimization:FilterPicker:A robust,broadband picker for real-time seismic monitoring and earthquake early warning[J]. Seismol Res Lett,83(3):531–540. doi: 10.1785/gssrl.83.3.531
Perol T,Gharbi M,Denolle M. 2018. Convolutional neural network for earthquake detection and location[J]. Sci Adv,4(2):e1700578. doi: 10.1126/sciadv.1700578
Ross Z E,Meier M A,Hauksson E,Heaton T H. 2018a. Generalized seismic phase detection with deep learning[J]. Bull Seismol Soc Am,108(5A):2894–2901. doi: 10.1785/0120180080
Ross Z E,Meier M A,Hauksson E. 2018b. P wave arrival picking and first-motion polarity determination with deep learning[J]. J Geophys Res:Solid Earth,123(6):5120–5129. doi: 10.1029/2017JB015251
Ruud B O,Husebye E S. 1992. A new three-component detector and automatic single-station bulletin production[J]. Bull Seismol Soc Am,82(1):221–237.
Saragiotis C D,Hadjileontiadis L J,Panas S M. 2002. PAI-S/K:A robust automatic seismic P phase arrival identification scheme[J]. IEEE Trans Geosci Remote Sens,40(6):1395–1404. doi: 10.1109/TGRS.2002.800438
Vidale J E. 1986. Complex polarization analysis of particle motion[J]. Bull Seismol Soc Am,76(5):1393–1405.
Zhu L J, Peng Z G, McClellan J. 2018. Deep learning for seismic event detection of earthquake aftershocks[C]//52nd Asilomar Conference on Signals, Systems, and Computers. Pacific Grove: IEEE: 1121–1125.
Zhu W Q,Beroza G C. 2018. PhaseNet:A deep-neural-network-based seismic arrival-time picking method[J]. Geophys Int J,216(1):261–273. doi: 10.1093/gji/ggy42
-
期刊类型引用(0)
其他类型引用(2)
计量
- 文章访问数: 491
- HTML全文浏览量: 127
- PDF下载量: 74
- 被引次数: 2
