An early earthquake alarming method using seismic P-wave double-parameter based on Bayesian theory
-
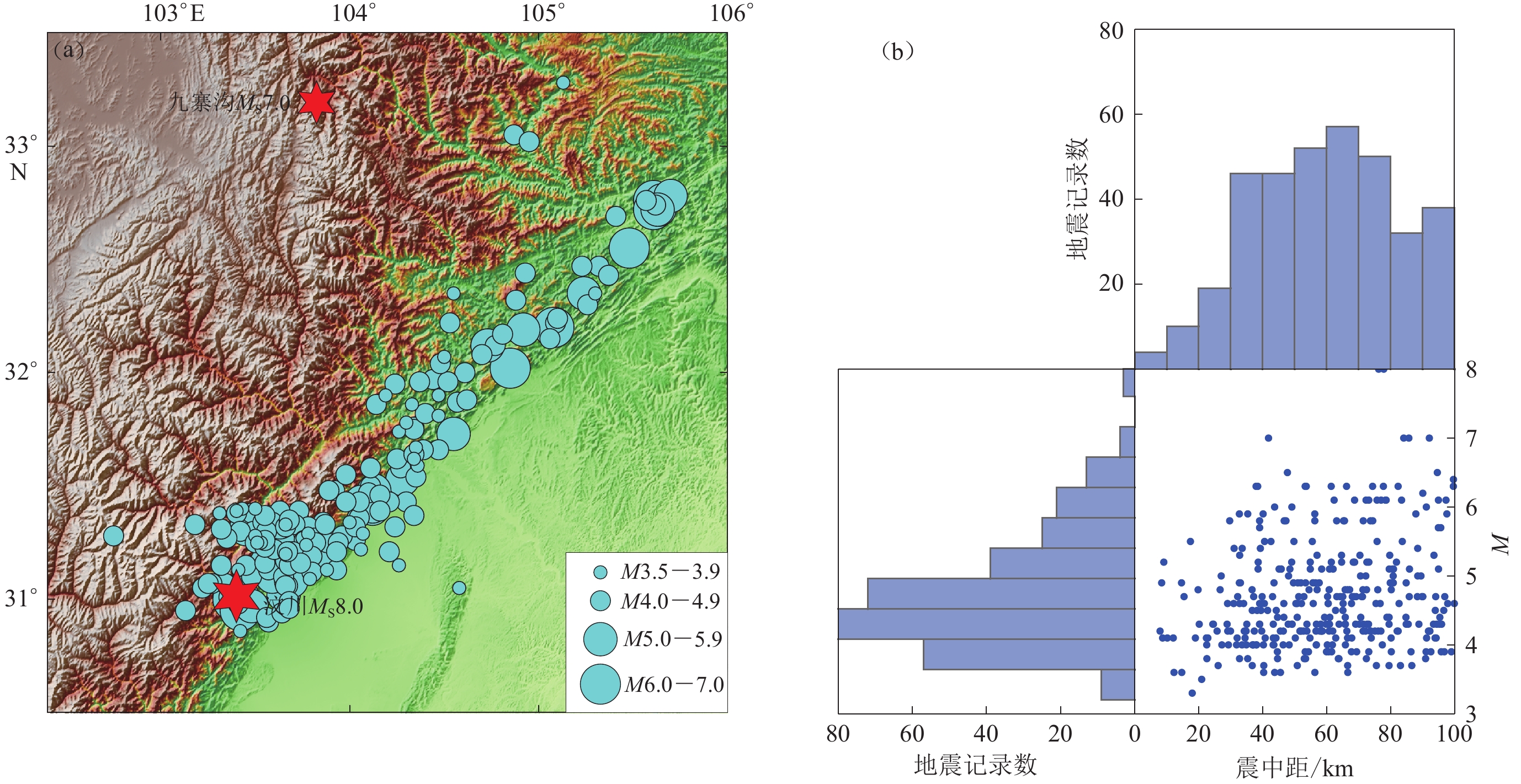
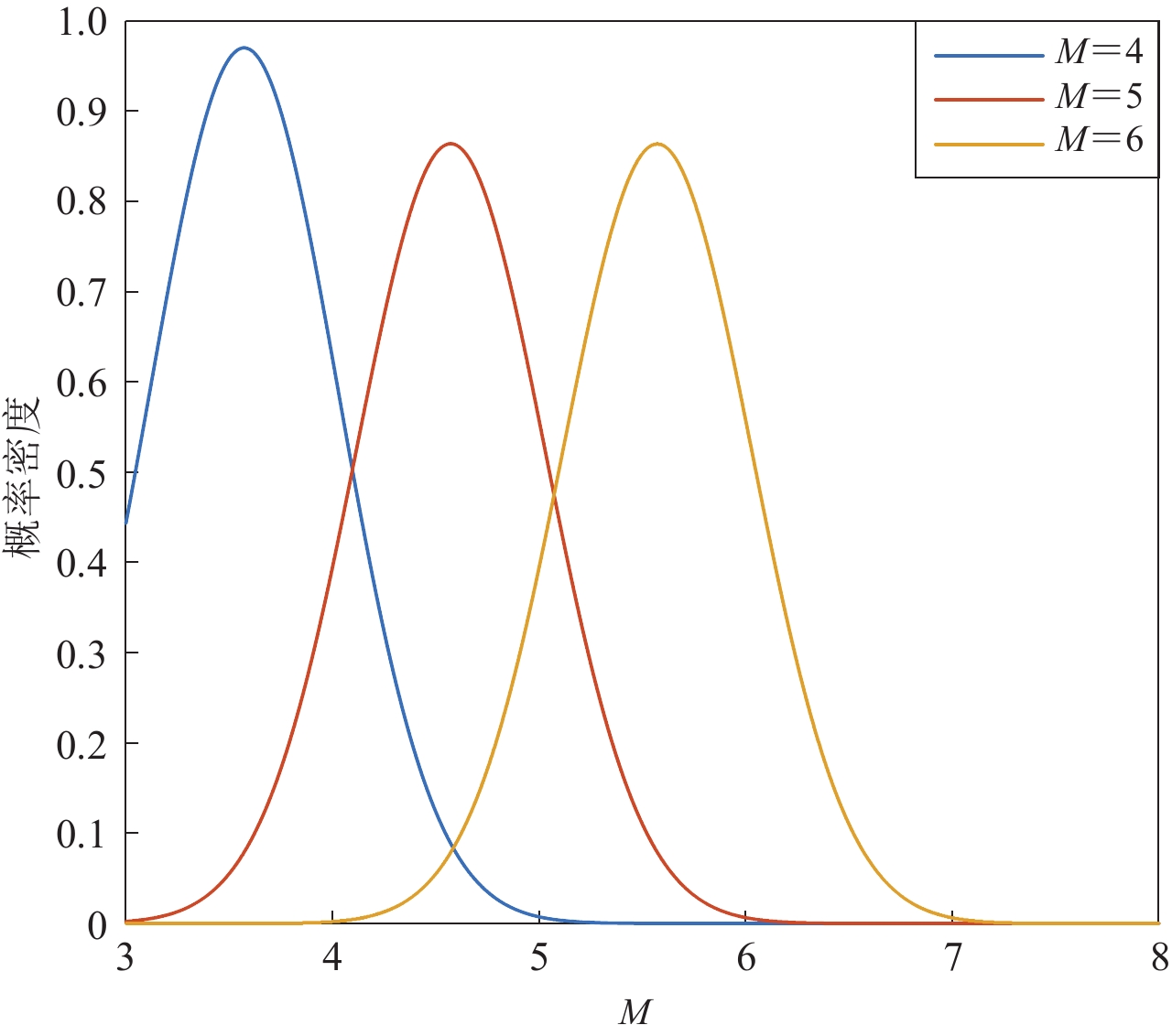
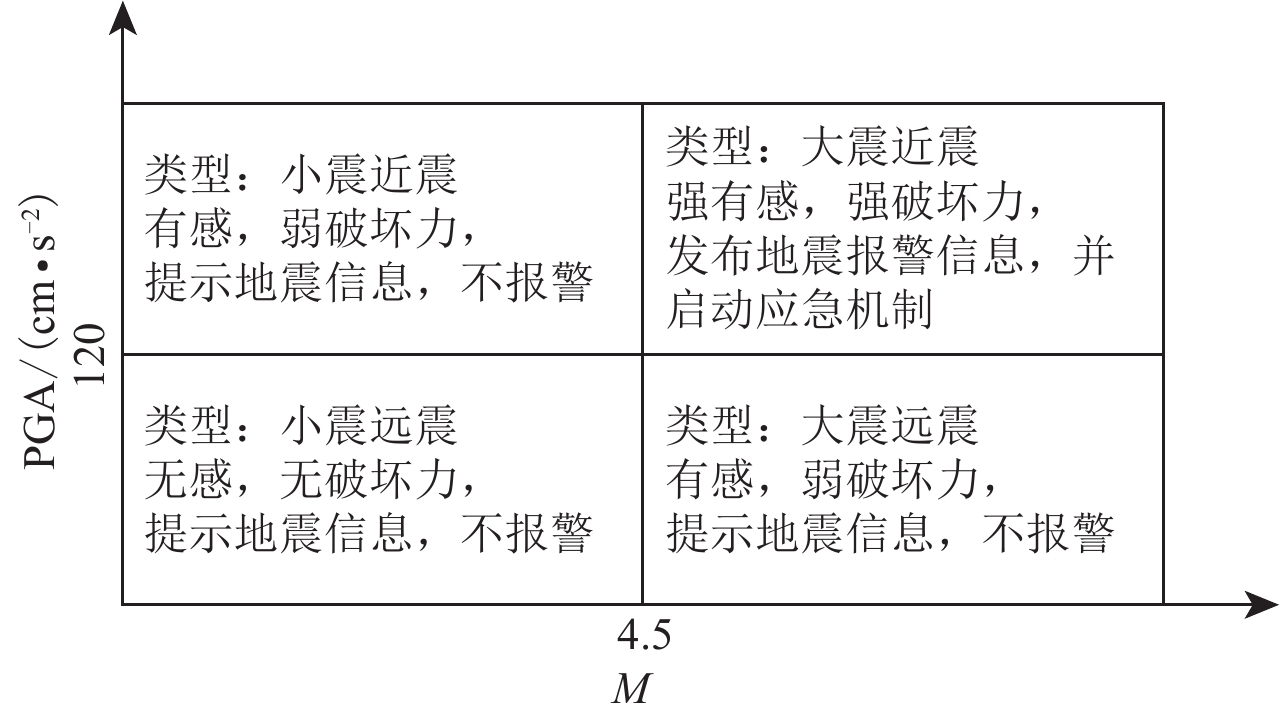
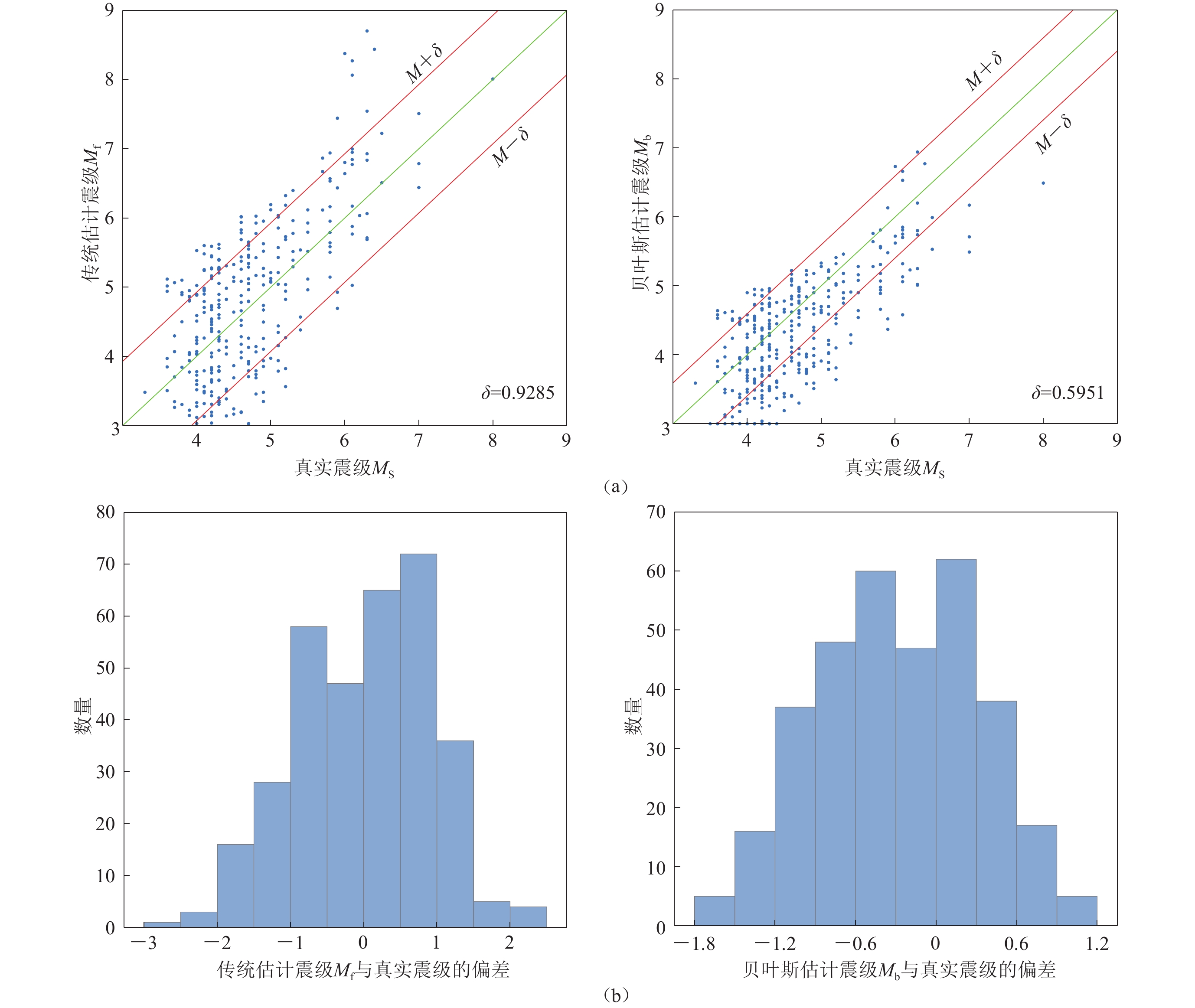
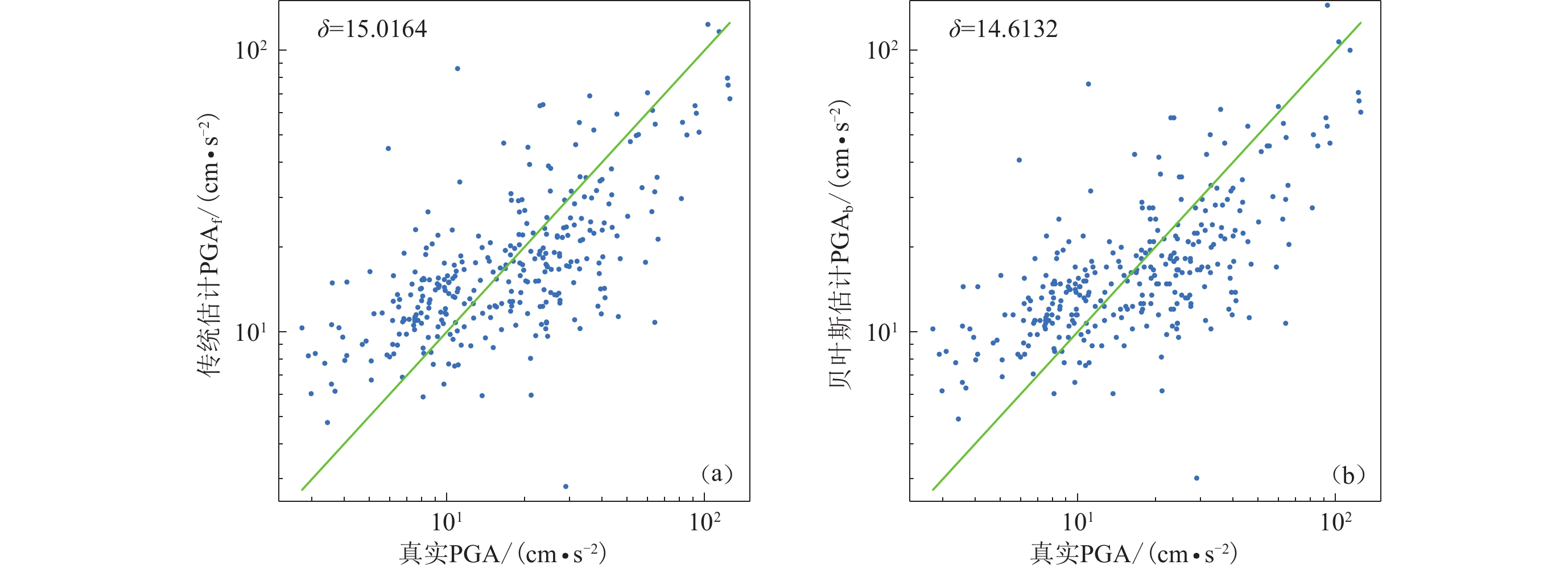
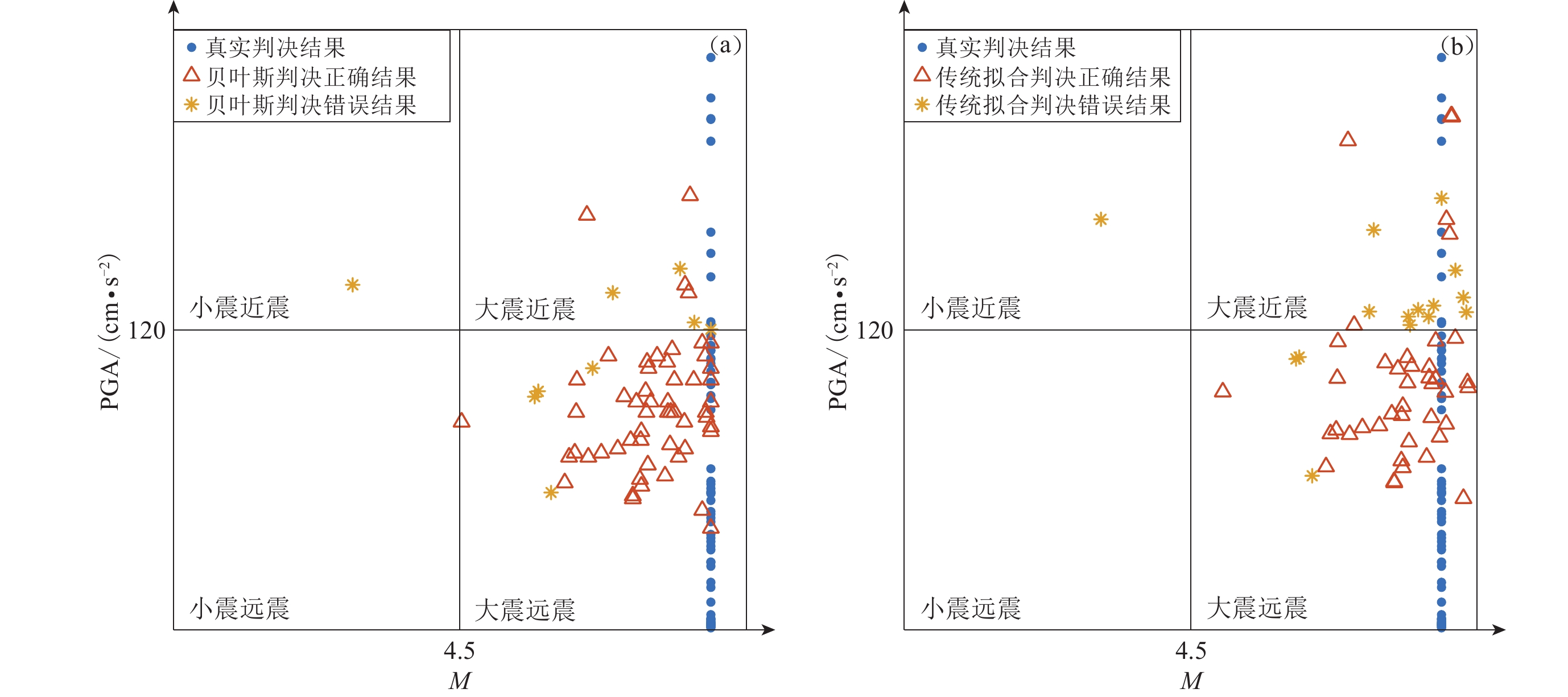
摘要: 为了及时、准确、可靠地发出地震预警信息，本文提出了一种基于贝叶斯理论的地震P波双参数预警方法。选取中国地震台网中心记录的四川地区的355条地震数据，统计P波触发后前3 s的P波平均周期τc和位移幅值Pd，结合贝叶斯理论建立震级和峰值加速度的预测模型，并以震级M4.5和峰值加速度为120 cm/s2为预警阈值，建立了地震危害性判别模型。与传统拟合方法进行对比仿真分析，并以汶川MS8.0地震为震例，进行地震危害性判别实验与分析。实验结果表明：本文提出的基于贝叶斯理论的地震 P 波双参数预警方法比传统拟合方法地震漏报率低 15.15%，可以快速、准确地估计震级与峰值加速度，并有效地评估地震的危害性，能够为地震监测预警提供数据支持和决策依据。Abstract: In order to send out earthquake alarm information timely, accurately and reliably, an early earthquake alarm method using P-wave double-parameter alarm method based on Bayesian theory is proposed in this paper. Based on 355 earthquake data recorded at Sichuan Province of China Earthquake Networks Center, the median period τc and ground motion amplitudes Pd in the first 3 seconds after P-wave triggering are calculated. Combined with Bayesian theory, the prediction model of magnitude and peak ground acceleration is established. Taking the magnitude M＝4.5 and PGA＝120 cm/s2 as the alarm threshold, the seismic hazard discrimination model is established. Compared with the traditional fitting method, the simulation analysis of earthquake early warming based on Bayesian theory, and then the Wenchuan MS8.0 earthquake is taken as an example to carry out the earthquake hazard identification. The experimentalresults show that early earthquake alarming method using seismic P-wave double-parameter based on Bayesian theory is 15.15% lower than the traditional fitting method, which can can quickly and accurately estimate the magnitude and peak acceleration, and effectively assess the hazard of earthquake, which can provide data support and decision-making basis for earthquake monitoring and alarming.
-
Key words:
- earthquake alarm /
- Bayesian theory /
- magnitude prediction /
- PGA prediction
-
图 1 选取地震的震中（a）和震中距、震级及地震记录数（b）的分布
Figure 1. Locations of earthquakes （a） and the number of earthquakes corresponding to different magnitudes and epicentral distances （b）
图 3 不同PGA的lgPGA概率密度分布
Figure 3. Probability density distributions of lgPGA with different PGA
图 5 实际震级与传统方法预测震级Mf和基于贝叶斯理论的预测震级Mb的比较（a）及其误差分布（b）
Figure 5. Comparison of value M with fitting predicted values Mf and Bayesian predictors Mb （a） and the error distribution （b） of predicted magnitude
图 6 真实值PGA与传统拟合预测值PGAf （a）和基于贝叶斯理论的预测值PGAb（b）的比较
Figure 6. Comparison of real values PGA with fitting predicted values PGAf （a） and Bayesian predictors PGAb （b）
图 7 基于贝叶斯理论的预测方法（a）和传统拟合方法（b）所得结果与真实数据判别结果的对比
Figure 7. Comparison of discrimination results by Bayesian theory method （a） and fitting method （b） with real data
表 1 实验数据与结果
Table 1. Experimental data and results
台站位置 贝叶斯理论预测结果 地震危害性判别结果 东经/° 北纬/° MS PGA/（cm·s−2） 贝叶斯方法 传统拟合方法 真实 102.20 29.90 7.03 79.43 大震远震 大震远震 大震远震 102.90 30.20 6.35 104.71 大震远震* 大震近震 大震近震 103.80 30.90 7.71 173.78 大震近震 大震近震 大震近震 102.90 30.10 7.11 107.15 大震远震 大震近震# 大震远震 102.20 28.30 6.91 53.70 大震远震 大震远震 大震远震 102.60 29.50 6.88 75.86 大震远震 大震远震 大震远震 102.10 29.40 6.02 69.18 大震远震 大震远震 大震远震 102.20 29.70 4.52 83.18 小震近震 小震近震 大震远震 103.50 30.60 3.00 138.04 小震近震* 小震近震* 大震近震 103.60 30.30 7.77 123.03 大震近震# 大震近震# 大震远震 102.40 29.30 7.94 85.11 大震远震 大震远震 大震远震 注：表中地震危害性判别结果中右上角标准为*的表示漏报；标注为#的表示误报。 
下载: 导出CSV
-
方嘉治,张颖,汪逵,董奕. 2020. 地震动场地影响校正在烈度速报中的应用研究[J]. 华南地震,40(3):17–26. Fang J Z,Zhang Y,Wang K,Dong Y. 2020. The research on application of site correction of ground motion in rapid reporting of seismic intensity[J]. South China Journal of Seismology,40(3):17–26 (in Chinese). 冯继威.2019. 大震地震动场的实时估计[D]. 哈尔滨: 中国地震局工程力学研究所:1–164. Feng J W. 2019.Real-time Estimation of the Ground Motion Field of Large Earthquakes[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Adminiistration: 1–164 （in Chinese）. 郭凯,温瑞智,彭克银. 2016. 地震预警系统的效能评估和社会效益分析[J]. 地震学报,38(1):146–154. doi: 10.11939/jass.2016.01.015 Guo K,Wen R Z,Peng K Y. 2016. Effectiveness evaluation and social benefits analyses on earthquake early warning system[J]. Acta Seismologica Sinica,38(1):146–154. 郝美仙,周银兴,张建中,张珂,尹战军. 2020. τc方法在内蒙古地区预警震级计算中的应用[J]. 中国地震,36(1):136–145. Hao M X,Zhou Y X,Zhang J Z,Zhang K,Yin Z J. 2020. Application of τc method in the early warning magnitude calculation in Inner Mongolia region[J]. Earthouake Research in China,36(1):136–145. 李世杰,吕悦军,刘静伟. 2018. 古登堡-里希特定律中的b值统计样本量研究[J]. 震灾防御技术,13(3):636–645. Li S J,Lü Y J,Liu J W. 2018. Research on b-value statistical sample size in Gutenberg Richter law[J]. Technology for Earthquake Disaster Prevention,13(3):636–645 (in Chinese). 龙承厚,赖敏,余桦,黎大虎. 2011. 地震有效峰值加速度与地震烈度相关性研究[J]. 四川地震,2011(2):26–31. Long C H,Lai M,Yu H,Li D H. 2011. Study on the correction between effective peak ground acceleration and seismic intensity[J]. Earthquake Research in Sichuan,2011(2):26–31 (in Chinese). 马强,李水龙,李山有,陶冬旺. 2014. 不同地震动参数与地震烈度的相关性分析[J]. 地震工程与工程振动,34(4):83–92. Ma Q,Li S L,LiS Y,Tao D W. 2014. On the correlation of ground motion parameters withseismic intensity[J]. Earthquake Engineering and Engineering Dynamics,34(4):83–92 (in Chinese). 宋晋东,教聪聪,李山有,侯宝瑞. 2018. 基于地震P波双参数阈值的高速铁路Ⅰ级地震警报预测方法[J]. 中国铁道科学,39(1):138–144. doi: 10.3969/j.issn.1001-4632.2018.01.19 Song J D,Jiao C C,Li S Y,Hou B R. 2018. Prediction method of first-level earthquake warning for high speed railway based on two-parameter threshold of seismic P-wave[J]. China Railway Science,39(1):138–144 (in Chinese). 武俊奇. 2016. 基于Bayes原理的渐进地面震动强度预警与P波特征参数研究[D]. 北京: 北京交通大学: 37–70. Wu J Q. 2016. Research on Progressive Ground Motion Intensity Warning Based on Bayes Principle and Characteristic Parameters of the P-Wave[D]. Beijing: Beijing Jiaotong University: 37–70 （in Chinese）. 张晁军,陈会忠,蔡晋安,侯燕燕,许洪华,李卫东. 2014. 地震预警工程的若干问题探讨[J]. 工程研究-跨学科视野中的工程,6(4):344–370. Zhang C J,Chen H Z,Cai J A,Hou Y Y,Xu H H,Li W D. 2014. Discussion on some issues of earthquake early warning engineering[J]. Journal of Engineering Studies,6(4):344–370 (in Chinese). 赵岑. 2013. P波预警中的震级预测和PGA、PGV估算研究[D]. 成都: 西南交通大学: 33–61. Zhao C. 2013. Study on the Characteristics of P-Wave to Estimate Magnitude and PGA, PGV in the Field of Earthquake Early Warning[D]. Chengdu: Southwest Jiaotong University: 33–61 （in Chinese）. 中国地震台网中心. 2020. 国家地震科学数据中心[DB/OL]. [2020-03-07]. http://data.earthquake.cn. China Earthquake Networks Center. 2020. China earthquake data center[DB/OL]. [2020-03-07]. http://data.earthquake.cn （in Chinese）. 周银兴,张素灵,郭凯,张岩. 2015. 高速铁路地震预警系统控车方案研究[J]. 震灾防御技术,10(1):116–125. doi: 10.11899/zzfy20150112 Zhou Y X,Zhang S L,Guo K,Zhang Y. 2015. High speed train control strategy in earthquake early warning system[J]. Technology for Earthquake Disaster Prevention,10(1):116–125 (in Chinese). Iervolino I,Convertito V,Giorgio M,Manfredi G,Zollo A. 2006. Real-time risk analysis for hybrid earthquake early warning systems[J]. J Earthq Eng,10(6):867–875. Kanamori H. 2005. Real-time seismology and earthquake damage mitigation[J]. Ann Rev Earth Planet Sci,33:195–214. doi: 10.1146/annurev.earth.33.092203.122626 Zollo A,Amoroso O,Lancieri M,Wu Y M,Kanamori H. 2010. A threshold-based earthquake early warning using dense accelerometer networks[J]. Geophys J Int,183(2):963–974. doi: 10.1111/j.1365-246X.2010.04765.x -
查看大图
计量
- 文章访问数: 335
- HTML全文浏览量: 118
- PDF下载量: 9
- 被引次数: 0