The centroid moment tensor solution of the 2021 MW7.5 Maduo，Qinghai，earthquake
-
-
关键词:
- 青海省玛多MW7.5地震 /
- 矩心矩张量解 /
- 断层参数 /
- 体波反演
-
引言
一般结构抗震设计时，仅考虑水平向地震作用的影响，往往忽视了竖向地震作用对结构产生的影响（王国权，2001；周正华等，2007）。在我国抗震设计中，仅遇到高烈度区或近场的大跨结构、悬臂结构和超高层工程结构才考虑竖向地震动的作用，将竖向地震动影响系数的最大值取为水平向的0.65倍（中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局，2010）。然而，近年来发生的几次强地震，在近场产生了较强的竖向地震动，部分竖向峰值加速度远远超过水平向峰值加速度。许多研究人员对这一特征进行了深入研究，其结果显示竖向与水平向的加速度谱比为一周期函数，而且与场地条件相关，短周期内的谱比大于2/3而长周期的谱比小于2/3 （Bozorgnia，Niazi，1995；Dimitriu et al，1999；周正华等，2003；Ambraseys，Douglas，2003；耿淑伟，陶夏新，2004；徐龙军，谢礼立，2007；贾俊峰，欧进萍，2010；李恒，秦小军，2010；谢俊举等，2010）。
近年来，南北地震带的川滇甘陕地区发生了大量的破坏性地震（汶川地震、玉树地震、芦山地震等），该地区布设了大量的强震台站，因而获得了大量的强震动数据。随着各种特殊结构物的大量兴建，竖向地震作用的研究受到了工程界的广泛重视（徐龙军，谢礼立，2007；李恒，秦小军，2010；齐娟等，2014）。目前，直接以我国大量强震动记录为数据基础进行的竖向地震动研究相对来说较少，为此，本文将以南北地震带川滇甘陕地区的强震动记录（M≥4）为研究对象，统计分析不同场地、震中距和震级等因素下的竖向与水平向的反应谱比，以期为工程结构的竖向抗震设计提供一定的参考依据。
1. 强震动记录来源与分组
本文选取南北地震带川滇甘陕地区最大峰值加速度（peak ground acceleration，简写为PGA）≥10 cm/s2 的强震动记录作为统计资料，剔除明显不合理的强震动记录并进行基线校正处理，最终获得研究区域内有详细场地条件的强震动记录802组。为了更好地统计分析，按照大震近场、大震远场、小震近场、小震远场的分类对所获取的数据进行分类（赵培培，2017；赵培培等，2017），其柱状图结果绘于图1。由于我国场地类别划分中Ⅱ类场地的分布范围较广，因此所得的Ⅱ类场地上的强震动记录较多，又由于该地区发生大震的次数有限，所以图1中小震远场Ⅱ类场地的强震动记录较多，这可能会对统计分析结果产生一定的影响。图2给出了不同类别场地上强震动记录随震级、震中距的变化趋势。
![]()
图 2 强震动记录随震级、震中距的分布图Figure 2. Distribution of strong ground motion recordings along with magnitude and epicentral distance2. 竖向与水平向反应谱比的总体特征
本文先计算出所用强震动记录中阻尼比为0.05的加速度谱。为了更好地分析竖向与水平向反应谱比的总体特征，对每组强震动记录计算谱比，然后再对谱比进行平均，其结果如图3所示。可见：竖向与水平向的谱比并不是规范规定的一个定值0.65，而是随着周期而变化；谱比P（T）总体的平均值为0.57，比规范所规定的0.65要偏小些；0—0.1 s周期内的谱比曲线存在一峰值0.71，远高于0.65；其余大部分周期内的谱比值均小于0.65。因此，竖向反应谱不应简单地取为水平向反应谱的一定值，而应考虑其随周期的变化。
3. 竖向与水平向反应谱比与场地类别的关系
大量的研究表明，竖向与水平向的谱比主要受场地类别的影响（耿淑伟，陶夏新，2004；贾俊峰，欧进萍，2010；李恒，秦小军，2010）。本文按照小震、大震、场地类别将同场地类别的强震动记录谱比进行平均，得到平均谱比曲线，如图4所示，其中小震的谱比曲线周期最长取到3 s，大震的谱比曲线周期最长取到10 s。表1列出了小震、大震情况下不同场地的平均谱比分段均值。
![]()
图 4 小震（a）、大震（b）情况下不同场地的平均谱比P曲线Figure 4. Average spectral ratio P curves for different sites on the condition of small （a） and strong （b） earthquakes表 1 不同场地各周期段的谱比平均值Table 1. Average spectral ratio for several periods on different sites周期T/s 谱比均值 Ⅰ类 Ⅱ类 Ⅲ类 小震 ＜0.1 0.57 0.74 0.58 ［0.1—1.0） 0.53 0.56 0.38 ［1.0—3.0］ 0.56 0.67 0.42 ［0—3.0］ 0.55 0.65 0.41 大震 ＜0.1 0.65 0.63 0.49 ［0.1—1.0） 0.63 0.54 0.36 ［1.0—3.0） 0.87 0.76 0.46 ［3.0—10.0］ 1.25 0.97 0.54 ［0—10.0］ 1.11 0.88 0.51 从图4可看出，场地类别对竖向与水平向谱比的影响比较显著，不同场地的平均谱比曲线的形状基本相似，Ⅰ类和Ⅱ类场地基本呈两边高、中间低的现象，但不同场地的谱比变化规律有所不同。小震时，Ⅱ类场地的谱比值基本上要高于Ⅰ类场地；0—0.1 s周期内，Ⅱ类场地的谱比值要高于 《建筑抗震设计规范》 （以下简称为“规范”）（中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局，2010）所规定的0.65，且峰值可达0.9，Ⅰ类场地和Ⅲ类场地的谱比值基本低于0.65；0.1—1.0 s周期内，除个别Ⅲ类场地的谱比值稍高于0.65外，其余情况下的谱比值均远远小于“规范”所规定的0.65；1.0—3.0 s周期范围内，Ⅱ类场地的谱比值大部分要高于0.65，其余情况均小于0.65，Ⅲ类场地的谱比值在周期大于0.1 s时产生了剧烈的上下振荡现象，造成这种现象的原因可能是该场地类别上的强震动记录数量较少而引起的统计偏差。大震时，随着场地变软，全周期段的谱比值不断地减小；Ⅲ类场地的谱比值在全周期内均小于0.65；周期大于1.0 s的范围内Ⅰ类和Ⅱ类场地的谱比值随周期的增大呈增大趋势，而且远远高于“规范”所规定的0.65，Ⅰ类场地的峰值高达1.41，Ⅱ类场地的峰值也在1.05。从大震统计的结果来看，该结果与谢俊举等（2010）关于汶川主震竖向与水平向谱比值的统计分析结果基本相近。
从表1可看出：小震时，Ⅱ类场地在＜0.1 s和1.0—3.0 s周期范围内的谱比均值高于0.65，其余情况下的谱比均值均小于0.65；大震时，不同周期段的谱比均值均随着场地变软而降低；全周期段的平均谱比值除Ⅲ类场地外均远远高于规范规定的0.65；除小于0.1 s周期外，Ⅰ类和Ⅱ类场地的中长周期平均谱比均值远高于0.65。
4. 竖向与水平向反应谱比与震级的关系
按照震级区间 ［ 4—5.5）， ［ 5.5—6.5）， ［ 6.5—7.5）和≥7.5分组，求取每个震级区间内的谱比均值，从而得到同场地不同震级区间内的平均谱比P（T）曲线，如图5所示；将图5中不同震级区间的谱比曲线进行分段求其平均值，结果列于表2。
![]()
图 5 不同场地条件下不同震级区间的平均谱比P曲线（a） Ⅰ类场地；（b） Ⅱ类场地；（c） Ⅲ类场地Figure 5. Average spectral ratio P curves for different magnitude intervals under different site condition（a） Class Ⅰ；（b） Class Ⅱ；（c） Class Ⅲ表 2 不同震级区间的平均谱比均值列表Table 2. Average spectral ratio of different magnitude intervals场地类别 周期T/s 平均谱比均值 4.0≤M＜5.5 5.5≤M＜6.5 6.5≤M＜7.5 M≥7.5 Ⅰ类 ＜0.1 0.53 0.67 0.69 0.63 ［0.1—1.0） 0.49 0.67 0.63 0.60 ［1.0—3.0） 0.50 0.79 0.83 0.87 ［3.0—10.0］ 0.43 0.81 1.06 1.19 ［0—10.0］ 0.45 0.79 0.97 1.07 Ⅱ类 ＜0.1 0.74 0.74 0.61 0.64 ［0.1—1.0） 0.57 0.54 0.55 0.54 ［1.0—3.0） 0.64 0.74 0.75 0.76 ［3.0—10.0］ 0.59 0.79 0.99 0.95 ［0—10.0］ 0.60 0.76 0.90 0.87 Ⅲ类 ＜0.1 0.57 0.58 – 0.40 ［0.1—1.0） 0.46 0.36 – 0.38 ［1.0—3.0） 0.50 0.37 – 0.45 ［3.0—10.0］ 0.54 0.59 – 0.44 ［0—10.0］ 0.53 0.53 – 0.44 从图5可看出，震级对不同场地条件下的竖向与水平向反应谱比有一定的影响。Ⅱ类场地下，反应谱比在周期小于1.0 s的范围内随震级的增大呈减小的趋势，在大于1.0 s的周期内随着震级的增大呈增大的趋势；Ⅱ类场地下，不同震级区间的谱比曲线均在0.1 s周期以内出现一峰值，而后迅速下降至谷底，谷底位置基本处于0.3 s周期，谷底过后则随着周期的增大谱比值有上升的趋势；Ⅱ类场地下，不同震级区间的谱比曲线表现为“马鞍形”，在＞3.0 s的周期内，谱比值随着震级的增大呈增大的趋势。当M≥5.5时，Ⅰ类与Ⅱ类场地不同震级的平均谱比在周期＞1.0 s时均远远大于0.65，而且平均谱比峰值远高于1.0。由于Ⅲ类场地上的强震数量过少，所以在分析震级对谱比的影响时存在一定的偏差，尚待收集更多的Ⅲ类场地资料进一步分析。
由表2的统计结果可以看出：Ⅰ类和Ⅱ类场地在M≥5.5的各个震级区间的平均谱比除个别外基本高于0.65，尤其是长周期段的谱比均值远高于“规范”规定的0.65定值，有些谱比均值甚至大于1.0；Ⅰ类和Ⅱ类场地在M≥5.5的整个周期内的谱比均值要远高于0.65；Ⅰ类和Ⅱ类场地的平均谱比均值随震级的增大而增大；Ⅲ类场地上的谱比均值基本在0.65以下。
5. 竖向与水平向反应谱比与震中距的关系
由于Ⅰ类和Ⅲ类场地的强震数据较少，本文仅就强震动数据比较丰富的Ⅱ类场地，对小震和大震下不同震中距的平均谱比进行统计分析，各分组的平均谱比曲线如图6所示；将不同震中距的平均谱比进行分段求其平均值，其计算结果列于表3。
![]()
图 6 小震（a）和大震（b）下不同震中距R范围内Ⅱ类场地的平均谱比P曲线Figure 6. Average spectral ratio P curves for small （a） and strong （b） earthquakes with different epicentral distance R ranges for the site class Ⅱ表 3 不同震中距R下的平均谱比值Table 3. Average spectral ratio within different epicentral distance R ranges周期T/s 平均谱比值 R＜20 km 20 km≤R＜60 km 60 km≤R＜100 km R≥100 km 小震 ＜0.1 0.67 0.75 0.77 0.69 ［0.1—1.0） 0.49 0.57 0.57 0.62 ［1.0—3.0］ 0.55 0.68 0.70 0.70 ［0.0—3.0］ 0.54 0.65 0.66 0.67 周期T/s 平均谱比值 R＜50 km 50 km≤R＜100 km 100 km≤R＜200 km R≥200 km 大震 ＜0.1 0.71 0.75 0.64 0.53 ［0.1—1.0） 0.52 0.53 0.55 0.55 ［1.0—3.0） 0.84 0.78 0.82 0.67 ［3.0—10.0］ 0.87 0.96 1.13 0.89 ［0.0—10.0］ 0.83 0.89 1.01 0.81 由图6可见：不同震中距的平均谱比曲线的形状基本一致，不管是小震还是大震，其谱比曲线均呈中间低、两边高的变化趋势，而且均在小于0.1 s周期内出现一峰值，在0.1—1.0 s周期内出现一波谷，在周期大于1.0 s后随着周期的增加不同震级的平均谱比值也在不断增大；小震情况下，不同震中距的平均谱比在短周期内的谱比峰值均在0.8以上，小震远场在周期大于1.0 s时的谱比峰值均高于0.65；大震情况下，0.1 s周期内、200 km震中距以内的谱比峰值高于0.65，周期大于1.0 s的平均谱比峰值均高于1.0，远远高于“规范”所规定的0.65定值，说明该地区的大震在周期大于1.0 s时具有较大的竖向地震作用。
从表3可知：不同震中距的平均谱比均值在0.1—1.0 s周期内均低于0.65，在周期＞1.0 s时小震远场的谱比均值高于0.65，在全周期内的谱比均值基本处于0.65左右；大震在0.1 s周期内、震中距小于100 km时的谱比均值大于0.65，在周期＞1.0 s时不同震中距的谱比均值均远远高于0.65，全周期内不同震中距的谱比均值均高于0.8，远远高于“规范”所规定的0.65，这说明“规范”中规定的0.65有待商榷。
6. 讨论与结论
本文以我国南北地震带川滇甘陕地区的M≥4.0强震动资料为基础，对竖向与水平向加速度反应谱比按照总体特征、场地、震级和震中距进行了统计分析。结果显示：竖向与水平向反应谱的谱比并不是某一定值，而是随周期的变化而变化；竖向与水平向反应谱比值会受到场地、震级和震中距等因素的影响，平均谱比值在大震时随着场地条件的变软而变小，Ⅱ类场地在周期大于1.0 s时的平均谱比值随震级的增大而增大，不管何种情况下，Ⅱ类场地的平均谱比曲线均呈两边高、中间低的特征。对谱比的分段求平均值可知，无论是何种分组情况，平均谱比均值在0.1—1.0 s周期内基本低于“规范”所规定的0.65定值， Ⅰ类和Ⅱ类场地下周期大于1.0 s时的大震谱比均值远远高于0.65，Ⅱ类场地下周期大于1.0 s时的小震远场以及5.5≤M＜6.5时的谱比均值均大于0.65； Ⅰ类和Ⅱ类场地下，全周期段的谱比均值基本上大于0.65。然而，大部分的抗震规范取水平向地震作用的0.65倍作为竖向地震作用，这显然不太合适，因此本文建议根据现有的竖向强震动记录，按照水平向反应谱的标定方式来确定竖向地震作用，从而将其应用于结构的竖向抗震设计。
此外，相对于Ⅱ类场地， Ⅰ类和Ⅲ类场地的强震动记录较少，因此关于Ⅰ类和Ⅲ类场地的统计分析有待于积累更多的强震动记录。
-
![]()
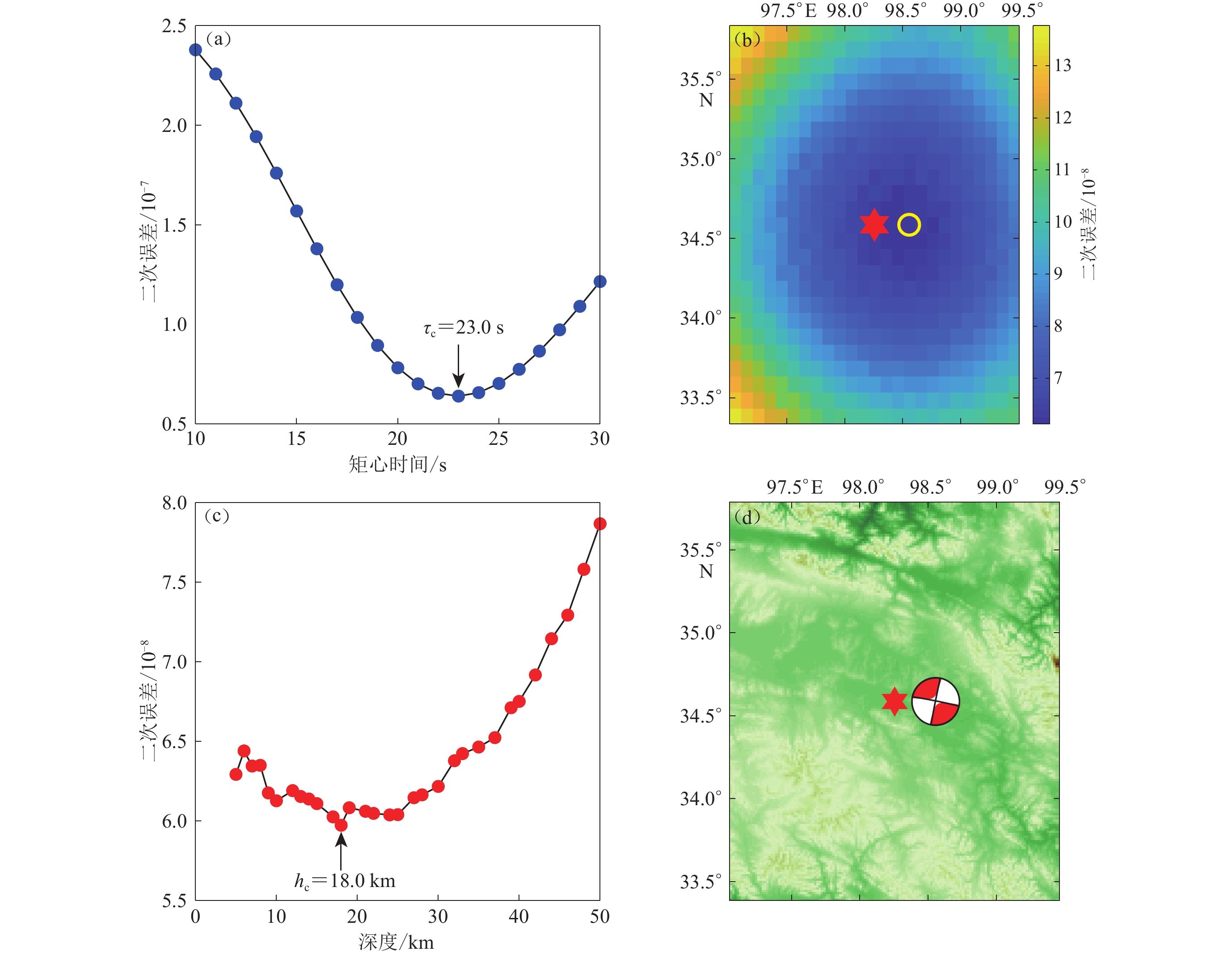
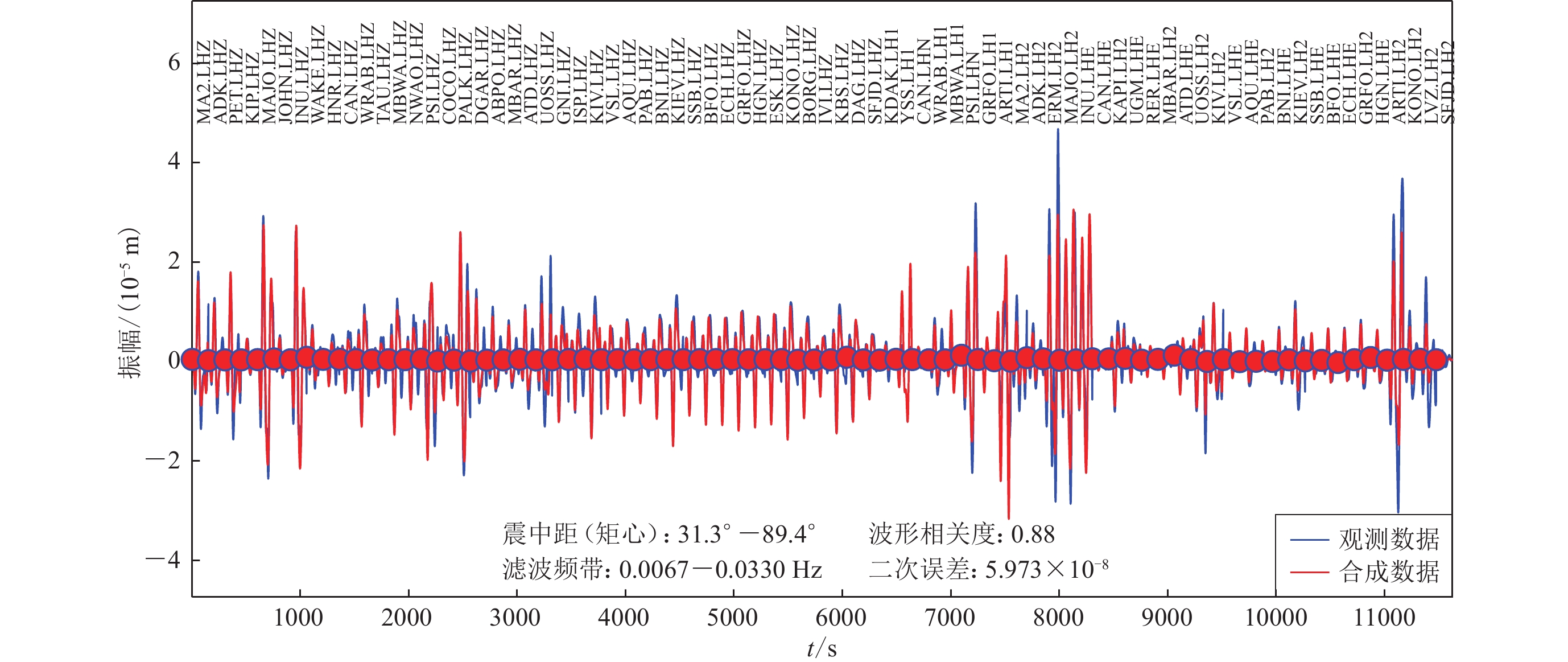
图 1 矩心矩张量解反演过程
（a） 矩心时间τc的搜索；（b） 矩心水平空间的搜索，黄色圆圈表示矩心水平坐标；（c） 矩心深度hc的搜索；（d） 矩心相对震中位置，红色沙滩球表示矩心矩张量解，红色星形表示震中
Figure 1. Inversion process of the centroid moment tensor
（a） Search for centroid time τc；（b） Search for the horizontal location of the centroid；（c） Search for centroid depth hc；（d） The centroid location （beach-ball） with respect to the instrumental epicenter （red hexagon）
![]()
图 2 矩心矩张量反演参数以及台站分布与反演结果
Figure 2. The parameters of the centroid moment tensor inversion，the station distribution and the inversion results
![]()
图 3 观测数据与合成数据的比较
Figure 3. Comparison between the observed （blue） and synthetic （red） waveforms
![]()
图 4 青海MW7.5地震矩心矩张量解的对比及较大余震分布
Figure 4. Comparison of the centroid moment tensor solutions of the MW7.5 Qinghai earthquake together with larger aftershocks
![]()
1 青海MW7.5地震矩心矩张量解的对比及较大余震分布（更新后）
1. Comparison of the centroid moment tensor solutions of the MW7.5 Qinghai earthquake together with larger aftershocks （updated）
表 1 GCMT，USGS与本研究所得青海玛多MW7.5地震的矩心矩张量解
Table 1 The centroid moment tensor solutions of the MW7.5 Maduo，Qinghai，earthquake from GCMT，USGS and this study
机构 矩张量/（1020 N·m） 矩心参数 Mrr Mtt Mpp Mrt Mrp Mtp τc/s 北纬/° 东经/° 深度/km GCMT （2021） −0.220 0.840 −0.620 0.186 −0.224 1.510 15.4 34.65 98.46 12 USGS （2021） −0.598 0.648 −0.050 −0.589 0.402 0.898 12.9 34.59 98.25 23.5 本文 −0.160 0.804 −0.643 −0.058 −0.063 1.745 23.0 34.59 98.55 18 
下载: 导出CSV
表 2 GCMT，USGS与本研究所得青海玛多MW7.5地震的最佳双力偶解
Table 2 The best double-couple solutions of the MW7.5 Maduo，Qinghai， earthquake from GCMT，USGS and this study
机构 标量地震矩
/（1020 N·m）双力偶成分
占比节面I 节面II 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° GCMT （2021） 1.710 95% 282 83 −9 13 81 −173 USGS （2021） 1.306 99% 92 67 −40 200 53 −151 本文 1.896 96% 281 88 1 191 89 178
下载: 导出CSV
1 GCMT，USGS与本研究所得青海玛多MW7.5地震矩心矩张量解
1 The centroid moment tensor solutions of the MW7.5 Maduo，Qinghai，earthquake from GCMT，USGS and this study
机构 矩张量/（1020 N·m） 矩心参数 Mrr Mtt Mpp Mrt Mrp Mtp τc/s 北纬/° 东经/° 深度/km GCMT （2021） −0.220 0.840 −0.620 0.186 −0.224 1.510 15.4 34.65 98.46 12 USGS （2021）（W震相） −0.598 0.648 −0.050 −0.589 0.402 0.898 12.9 34.59 98.25 23.5 USGS （2021）（矩心解） −0.454 0.963 −0.509 −1.252 0.718 1.618 15.79 34.81 98.25 26 本文 −0.160 0.804 −0.643 −0.058 −0.063 1.745 23.0 34.59 98.55 18
下载: 导出CSV
2 GCMT，USGS与本研究所得青海玛多MW7.5地震最佳双力偶解
2 The best double-couple solutions of the MW7.5 Maduo，Qinghai，earthquake from GCMT，USGS and this study
机构 MW 标量地震矩
/（1020 N·m）双力偶
成分占比节面I 节面II 走向
/°倾角
/°滑动角
/°走向
/°倾角
/°滑动角
/°GCMT （2021） 7.42 1.710 95% 282 83 −9 13 81 −173 USGS （2021）（W震相） 7.34 1.306 99% 92 67 −40 200 53 −151 USGS （2021）（矩心解） 7.51 2.323 82% 99 79 −38 197 53 −166 本文 7.45 1.896 96% 281 88 1 191 89 178
下载: 导出CSV
-
张喆, 梁皓, 许力生. 2020. 2020年6月23日墨西哥MW7.4 地震矩心矩张量解 [J]. 地震学报, 42（4）: 504–508. doi: 10.11939/jass.20200104. Zhang Z,Liang H,Xu L S. 2020. The centroid moment tensor solution of the 23 June 2020 MW7.4 Mexico earthquake[J]. Acta Seismologica Sinica,42(4):504–508 (in Chinese).
张喆,许力生. 2021. 2021年2月13日日本本州东海岸MW7.2地震矩心矩张量解[J]. 地震学报,43(2):255–259. doi: 10.11939/jass.20210025 Zhang Z,Xu L S. 2021. The centroid moment tensor solution of the February 2021 MW7.2 earthquake in East Coast of Honshu,Japan[J]. Acta Seismologica Sinica,43(2):255–259 (in Chinese).
GCMT. 2021. Global CMT catalog[EB/OL]. [2021-05-21]. https://www.globalcmt.org/CMTsearch.html.
USGS. 2021. M7.3: Southern Qinghai, China[EB/OL]. [2021-05-21]. https://earthquake.usgs.gov/earthquakes/eventpage/us7000e54r/executive.
Wang R J. 1999. A simple orthonormalization method for stable and efficient computation of the Green’s function[J]. Bull Seismol Soc Am,89(3):733–741.
-
期刊类型引用(6)
1. 孙丽娜，齐玉妍，张合. 河北及邻区地震类型特征及震后早期最大余震预估方法的研究. 震灾防御技术. 2025(01): 63-76 . 
百度学术
2. 周依，曹筠，马旭东，单连君. 唐山老震区现今地震活动特征. 地震研究. 2024(03): 430-440 . 百度学术
3. Jinxin Hou，Yunpeng Zhang，Liwei Wang，Zhirong Zhao. Earthquake relocation using a 3D velocity model and implications on seismogenic faults in the Beijing-Tianjin-Hebei region. Earthquake Research Advances. 2024(02): 55-64 . 必应学术
4. 周依，马旭东，王想. 唐山地区地震视应力时空变化特征. 大地测量与地球动力学. 2024(10): 1059-1063 . 百度学术
5. 曹筠，周依，高晨，刘书峰，陈安，张素欣，冯向东，吴鹏，陈肇东. 2020年7月12日河北唐山5.1级地震发震断层判定及其区域构造意义. 地震地质. 2024(05): 993-1011 . 百度学术
6. 陈婷，余海琳，章阳，孙丽娜. 唐山地区三维b值分布特征研究. 华北地震科学. 2022(01): 34-40 . 百度学术
其他类型引用(1)
-
其他相关附件
计量
- 文章访问数: 1774
- HTML全文浏览量: 930
- PDF下载量: 246
- 被引次数: 7
