引言

地电阻率前兆观测已在我国开展40多年，结果表明，大震前在震源区及其附近一般都会出现视电阻率的变化，是一种比较可靠的地震前兆观测(张国民等，2001；杜学彬，2010)． 然而，地电阻率观测大部分采用对称四极装置在地表进行，这样的观测系统观测到的视电阻率变化是观测范围内位于不同深度的各地层电阻率变化的综合反映． 众所周知，气候交替变化会使地下水位和近地表层介质含水量发生变化，进而导致浅部地层介质电阻率发生变化，显然这种变化与地震孕育无关，反而会对地电阻率观测结果造成干扰． 而孕震过程或地壳构造运动会导致观测区深部地层电阻率发生变化，按照目前的认识，这种变化才具有地震前兆意义． 为获得深部电阻率变化，须加大供电极距和供电电流强度，加大观测环境保护的范围，但这与地方经济建设之间会产生矛盾．

解决上述矛盾的方法之一是深埋装置电极(井下)观测. 过去30多年已有研究人员进行过深埋装置电极电阻率观测的实验研究(苏鸾声等，1982；刘允秀等，1985；孟庆武，阎洪朋，1991)，但由于缺乏理论研究，对实验结果的分析难以深入. 聂永安等通过求得水平层状介质点源激励解析解的方式，从理论上研究了3层结构在地表和基岩中四极对称电阻率观测结果与装置深度、 供电极距之间的关系(聂永安，姚兰予，2009；聂永安等，2010). 解滔等(2012)利用这一方法对井下电阻率观测中地表电流的干扰影响进行了计算分析，研究结果对实施井下电阻率观测时，为压制地表电流干扰影响而如何选择台址电性结构和电极埋深、 确定干扰源避让距离等方面具有参考意义. 但上述方法对3层以上的复杂结构未进行分析．

本文以边界积分方程为数学工具，利用物理意义明确的影响系数概念，模拟研究四极装置在地层中不同深度时影响系数的变化规律． 边界积分方程不仅能对任意层数的一维介质进行模拟，也适用于二维、 三维介质的研究；影响系数则可以直观地反映不同地层电阻率变化对观测到的视电阻率变化的影响程度. 因此观测装置在不同深度的影响系数对井下电阻率观测中装置电极埋设深度的选择具有较好的参考及指导意义．

1.   二维边界积分方程与影响系数简介

1.1   边界积分方程

采用的二维正演数值模拟方法是作者提出的边界积分方程法. 该方法在以往的研究中已就二维电性结构从理论和数值模拟两方面证明了其准确性(毛先进，鲍光淑，1998)．

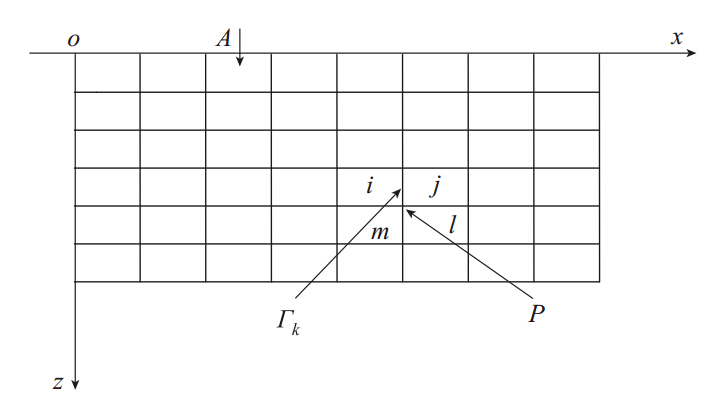
对地下介质电性结构为二维、 点电流源(可在地表或地下)供电这种常见的情况(图1)，剖面上任意一网格节点P(点电流源所在位置A点除外)的二维电位u_p(λ)满足如下边界积分方程：

图  1  二维地电阻率模型A点箭头表示点电流源,P表示第i,j,l,m等4个单元的共同顶点(网格节点),Γ_k表示第k层边界

Figure  1.  Two-dimensional model of geoelectrical resistivity The arrow at A presents current source，P presents the conjunct vertex of the ith，jth，lth，mth elements，Γ_k presents the kth boundary

下载: 全尺寸图片 幻灯片

通过如下定义的傅里叶逆变换，可将二维电位转换为可以用仪器测量的三维电位U_P，即

式(1)、 式(2)中: f_P为与P点相邻各单元的电导率σ_i，σ_j，σ_l，σ_m的线性组合；λ为与空间傅里叶变换相联系的波数；I为点源电流强度；A为点电源位置；φ为格林函数，等于单位强度的点源在均匀半空间内激发的电位分布，其“源”在P点；Δσ_k为边界Γ_k两边的电导率之差；n为Γ_k的正方向；N为边界总数；σ₀为背景电导率．

正演计算，即已知源分布和各单元电导率，求解空间电位． 按照式(1)分别给出所有节点的边界积分方程，离散后可得线性方程组

式中：U =(u₁，u₂，…，u_NJ)^T，N_J为节点总数；A 为N_J阶系数方阵；B 为由格林函数和点电流源位置确定的N_J阶列向量． 求解式(3)即可得到各节点的二维电位，然后据式(2)作傅里叶逆变换，可求得各节点电位，进一步计算可得到视电阻率等参数．

图1中每个单元的电导率可根据实际情况或需要给定，因此边界积分方程可以对任意分布的电阻率模型作模拟计算．

1.2   影响系数

对于一维情形，假定地电阻率观测区是水平层状介质，共n层，各层电阻率为ρ_i，层厚为h_i. 又假定底层的层厚无限大，即h_n→∞，在地表或地下四极对称装置观测到的视电阻率ρ_s为地下各层电阻率和层厚的函数，即

假定仅仅是电阻率变化，层厚保持不变． 对式(4)取对数且求微分得到

令

式中，S_i为影响系数，表示在给定的观测装置下，第i层电阻率变化对观测到的视电阻率变化的贡献大小，可以由介质电性参数和装置参数计算出来． 于是式(5)可改写为

2.   影响系数随观测装置埋深的变化

影响系数与地电阻率结构有关，实际的地电阻率结构因场地而异． 定性来看，水平层状电阻率分层均匀结构存在下伏高阻与下伏低阻两种情形． 在地表观测的情况下，一般认为与下伏低阻结构相比，下伏高阻结构不利于获得深部电阻率变化的信息. 在地下观测时是否也是如此，下文将对下伏高阻与下伏低阻两种情形分别进行研究．

2.1   下伏低阻结构计算结果

给定一个7层的水平层状电阻率分层均匀结构模型，第1—7层电阻率依次为80，60，90，120，60，160，50 Ω · m，第1—6层厚度均为50 m，第7层厚度→∞. 计算中设定对称四极 装置中供电极A，B与测量极M，N在地表或在地下同一深度，取AB=950 m，MN=300 m．

表1给出了对称四极装置在地表时常用的转换函数法(钱家栋等，1986)与本文采用的边界积分方程法分别计算得到的结果. 下面这两种方法分别称为方法1和方法2． 由表1可见，对下伏低阻结构，无论是视电阻率还是各层影响系数，两种方法的计算结果都十分相近，进一步表明了方法2的准确性．

表  1  对称四极装置在地表时影响系数的计算结果(下伏低阻结构)

Table  1.  The calculation results of influence coefficient with the observation array on the ground (The resistivity of the bed strata is the lowest)

下载: 导出CSV 

| 显示表格

表2给出了对称四极装置在地表和地下不同深度时，用方法2计算得到的下伏低阻结构各层介质的影响系数． 由表2可见两个显著特点： ① 底层介质影响系数S₇随装置埋深的增加而单调增加，这表明观测装置埋得越深，观测到底层电阻率变化的能力越强；② 底层以上各层介质影响系数(S₁—S₆)并不是随装置埋深的增加而单调减小，而是表现为“减小—增加—减小”或“增加—减小—增加—减小”起伏变化的特点，只有装置埋深进入底层以后影响系数才随装置埋深而单调减小． 以装置埋深在0，50，100，150 m为例(表2)，地表层的影响系数S₁的值分别为0.083 6，0.080 9，0.106 9，0.110 7，呈现“减小—增加”特征，底层的影响系数S₇的值分别为0.165 6，0.175 8，0.204 8，0.281 5，呈单调“增加”特征. 如果装置埋深为100 m，无论是从S₁的绝对值还是从S₁与S₇的比值来看，不仅不会压制反而会放大表层的变化． 上述特点①表明装置埋设深度对压制表层变化能力的影响是明显的，总体上观测装置埋得越深，压制表层影响、 观测到底层电阻率变化的能力越强；特点②表明装置埋设深度在底层上表面以上时，在某些深度上不仅不会压制反而会放大表层的变化．

表  2  利用本文方法得到的下伏低阻结构各层介质影响系数的计算结果

Table  2.  The calculation results of influence coefficient with the observation array in different depth using the method proposed in this paper (The resistivity of the bed strata is the lowest)

下载: 导出CSV 

| 显示表格

2.2   下伏高阻结构计算结果

将上述下伏低阻结构中底层(即第7层)电阻率变为200 Ω · m，其它各层电阻率及层厚度不变，依然设定对称四极装置中供电极A，B与测量极M，N在地表或在地下同一深度，取AB=950 m，MN=300 m．

表3给出了对称四极装置在地表时分别用方法1和方法2计算得到的各层影响系数． 可见对下伏高阻结构，无论是视电阻率还是各层影响系数，两种方法的计算结果均十分相近．

表  3  对称四极装置在地表时影响系数的计算结果(下伏高阻结构)

Table  3.  The calculation results of influence coefficient with the observation array on the ground (The resistivity of the bed strata is the highest)

下载: 导出CSV 

| 显示表格

表4给出了对称四极装置在地表和地下不同深度时，用方法2计算得到的下伏高阻结构各层介质的影响系数． 可见其具有与上述下伏低阻结构相同的两个特点.

表  4  利用本文方法得到的下伏高阻结构各层介质影响系数的计算结果

Table  4.  The calculation results of influence coefficient with the observation array in different depth using the method proposed in this paper (The resistivity of the bed strata is the highest)

下载: 导出CSV 

| 显示表格

3.   观测装置在底层时影响系数随供电极距的变化

上述研究表明，装置埋深进入底层后，埋深越大，压制表层影响和观测到底层电阻率变化的能力越强，但观测系统建设与维护的技术难度也随之增大，因此有必要研究观测装置在底层适当深度时影响系数随供电极距的变化．

表5和表6分别给出了下伏低阻与下伏高阻结构观测装置埋深350 m(即在底层顶面以下50 m)时各层介质的影响系数随供电极距AB从250 m到950 m的计算结果． 据表5和表6可知，观测装置在底层时，总体来看底层介质影响系数S₇随供电极距AB的减小而增加，第1—3层介质的影响系数则单调减小．

表  5  观测装置埋深350 m时不同供电极距下各层介质影响系数的计算结果(下伏低阻结构)

Table  5.  The calculation results of influence coefficient with the observation array in depth of 350 m(The resistivity of the bed strata is the lowest)

下载: 导出CSV 

| 显示表格

表  6  观测装置埋深350 m时不同供电极距下各层介质影响系数的计算结果(下伏高阻结构)

Table  6.  The calculation results of influence coefficient with the observation array in depth of 350 m(The resistivity of the bed strata is the highest)

下载: 导出CSV 

| 显示表格

按上述模型参数，以下伏低阻结构为例(表5)，在AB=250 m时，假定第1—2层介质电阻率受到降雨或潜水位变化等因素影响均减小90%，而第3—6层为不受影响层，其电阻率不变；再假定同时底层介质电阻率受构造运动影响减小5%，按式(5)计算，其视 电阻率的变化率dρ_s/ρ_s=-0.046 03，即-4.603%. 其中底层电阻率变化的贡献是S₇×(-5%)=0.863 0×(-5%)=-4.315%，第1—2层电阻率变化的贡献是(S₁+S₂)×(-90%)= 0.003 2×(-90%)=-0.288%. 因此观测到的电阻率变化主要反映了底层的变化，从而压制了浅层干扰，可以很好地观测到底层的变化． 如果AB=950 m，则dρ_s/ρ_s=-0.099 295，即-9.929 5%. 其中底层电阻率变化的贡献是S₇×(-5%)=0.729 5×(-5%)=-3.647 5%，第1—2层电阻率变化的贡献是(S₁+S₂)×(-90%)=0.069 8×(-90%)=-6.282%，表明压制浅层干扰的效果不理想． 这说明，即便装置埋设在底层，若供电极距AB选择不合适也达不到理想的压制表层干扰及观测到底层变化的目的． 对下伏高阻结构，利用表6的数据分析，也可以得到类似的结果．

显然，合适的供电极距与电阻率结构有关，应在查明电阻率结构后通过理论计算与分析再确定．

4.   讨论与结论

本文采用水平层状介质模型，应用边界积分方程法计算了不同装置埋深、 不同装置参数下的影响系数及其与结构参数间的关系． 对称四极装置中供电极A，B与测量极M，N在地表或在地下同一深度时，得到如下结论：

1)对水平层状电阻率分层均匀介质，底层介质影响系数随装置埋深的增加而单调增加，即观测装置埋得越深，观测到底层电阻率变化的能力越强；底层以上各层介质影响系数并不是随装置埋深的增加而单调减小，而是表现为“减小—增加—减小”或“增加—减小—增加—减小”起伏变化的特点．

2)装置埋设深度对压制表层变化能力的影响是明显的，总体上观测装置埋得越深，压制表层影响及观测到底层电阻率变化的能力越强；装置埋设深度在底层上表面以上时，在某些深度上不仅不会压制反而会放大表层的变化．

3)装置埋设到底层时，供电极距AB选择不合适也达不到理想的压制表层干扰与观测到底层变化的目的． 合适的供电极距与电阻率结构有关，应在查明电阻率结构后通过理论分析与计算再确定．

需要说明的是，本文并不是企图而且也没有给出深埋装置电极电阻率观测中确定电极埋设深度的简单的、 公式化的方法. 实际上本文的研究结果表明，影响系数与电阻率结构、 电极埋深、 电极距等关系密切. 因此，针对一个给定的观测场地，如何选择合适的电极埋深、 电极距等参数，需要在了解其电阻率结构后通过影响系数的计算结果再来分析确定．

本文研究过程中与中国地震局兰州地震研究所梁子斌副研究员进行了有益的讨论，审稿专家对本文提出了宝贵的修改意见，在此一并致以诚挚的谢意．