Earthquake loss prediction based on random forest algorithm
-
摘要:
针对现有的基于实际震害评估的大多研究仅限于某特定区域和某种结构类型，且所采用的数据样本量也十分有限，本文基于随机森林模型，采用2011年3月11日东日本MW9.0地震的37万8 037条建筑物实际震害数据，利用美国应用技术协会发布的地震震害等级划分标准（ATC-13）预测了建筑物地震破坏所引起的损失，对建筑物损失的影响因素进行了特征重要性分析。结果显示：通过合成少数类过采样技术（SMOTE）解决数据不均衡和贝叶斯优化超参数之后，得到了基于随机森林的预测模型测试集的准确率为68.8%，轻微破坏、中等破坏、严重破坏、倒塌等四种破坏等级的召回率分别为65.0%，53.6%，74.8%，81.8%；考虑生命安全性能将模型转换为二分类之后，模型准确率进一步提高至87.5%，极大地改善了现有研究应用于建筑损失预测中数据样本量受限、数据不均衡等导致的最严重破坏等级精度低等问题。对随机森林模型特征重要性的研究表明：震中距、峰值加速度和vS30是最影响模型输出的特征。
Abstract:Rapid assessment of building damage and its severity after an earthquake is crucial for emergency response and recovery. Accurate earthquake damage assessment is crucial for pre-earthquake disaster prevention and mitigation, post-earthquake disaster relief, and rapid reconstruction. Most existing studies based on actual earthquake damage assessment are limited to a specific region and a particular structure type, and the number of data samples used is also limited, resulting in subpar generalization performance for the model. Many factors affect the loss of buildings due to earthquakes. Traditional methods cannot fully consider the complex mapping relationship between the influencing factors. Therefore, finding a method to quickly and accurately assess building damage is essential. Machine learning provides a data-driven artificial intelligence method that can handle complex nonlinear relationships between input and output parameters by learning the underlying laws of big data. This paper proposes an earthquake damage prediction model based on combination of Bayesian optimization algorithm, synthetic minority over-sampling technique （SMOTE）, and random forest algorithm. The core of the Bayesian optimization algorithm takes prior knowledge into account. It can continuously update and iterate until the optimal parameter combination is fitted, solving the problem of slow efficiency of traditional parameter adjustment. The core of the SMOTE method is to generate data samples of a few categories, solving the problem of uneven distribution of data samples. Based on the random forest model, this paper uses 378 037 actual building damage data from the March 11, 2011, MW9.0 Tohoku-Oki, Japan earthquake, comprehensively considers multidimensional building information such as ground shaking information, site information, and structural characteristics, and uses the earthquake damage classification issued by the American Applied Technical Council （ATC-13）. This model can predict the damage caused by earthquake damage to buildings and analyze the feature importance of factors affecting building damage. The results show that after using SMOTE method to solve data imbalance and the Bayesian approach to optimize hyper-parameters, the accuracy on the test set of the random forest-based prediction model is 68.8%, and the recall rates for minor damage, moderate damage, severe damage and collapse are 65.0%, 53.6%, 74.8%, and 81.8%, respectively; the accuracy of the model is further increased to 87.5% by considering the life safety performance to convert the model to dichotomous classification, which significantly improves the existing research problems in building loss prediction, such as limited data, lack of regional generalization, lack of diversity in building attributes, imprecise classification of damage levels and low accuracy of the most severe damage state. The study of the importance of random forest features showed that the epicenter distance, PGA and vS30 have the most significant influences on the model output.The earthquake damage assessment model established by this study can achieve rapid and relatively accurate prediction of building damage caused by earthquakes, which is beneficial for pre-earthquake planning and timely rescue after the earthquake.
-
Keywords:
- building loss data /
- random forest /
- earthquake loss prediction /
- feature importance
-
引言
地震破坏对建筑物的安全和使用寿命构成严重威胁。准确地预测建筑物的破坏程度乃至建筑物的损失，可为震前规划和震后救援等提供决策性的依据。
传统的建筑物损失评估方法主要包括经验法、统计法（孙柏涛，胡少卿，2005；于红梅等，2006）和分析方法（Singhal，Kiremidjian，1996）等。经验法主要通过专家的工程经验对建筑物损失进行评估，例如：美国应用技术协会$ ［ $Applied Technology Council （缩写为ATC），1985$ ］ $利用Whitman等（1973）的破坏概率矩阵方法，针对美国加州地震易损性，采用问卷形式综合了50多名专家的意见得到建筑物损失估计系数；Miyakoshi等（1997）基于1995年阪神地震的建筑物破坏数据，采用回归分析方法得到易损性曲线，并将其用于未来的震害预测。经验法一般耗时长、工作量大且受到震害数据不足等的影响，未考虑影响建筑物损失的特征重要性。统计法是根据真实震害数据统计评估建筑物损失破坏，但由于缺少大量详实的震后建筑物群体破坏资料，需要进一步提高建筑物特征的深度和广度。分析方法指使用有限元分析来量化结构在地震动作用下的动力响应，继而依据响应结果给出结构损失，但分析结果取决于给定的参数和假设，缺乏与真实地震损失对比验证（Calvi et al，2006），无法考虑真实地震的不确定性。综上所述，上述三种建筑物损失评估方法均忽略了地震潜在的不确定性，缺少大量真实地震破坏资料的对比验证，更未考虑各影响因素对地震破坏的影响程度，因此存在一定的缺陷。
近年来机器学习在地震工程领域得到了广泛应用（鲍跃全，李惠，2019；隗永刚，蒋长胜，2021；杨旭等，2021；Harirchian et al，2021a），但其应用于地震损失预测的研究尚处于起步阶段。Mangalathu等（2020）基于2014年美国加利福尼亚州纳帕（Napa）南部地震造成的2 276栋建筑物破坏数据，依据ATC-20对受损建筑物进行分类，基于随机森林（random forest，缩写为RF）方法预测建筑物遭受的地震破坏，虽然测试集总体的准确率达到66.0%，但倒塌破坏等级的预测准确率仅为13.0%；Roeslin等（2020）基于2017年墨西哥普埃布拉（Puebla）地震造成的237栋建筑物的破坏数据，根据欧洲98版地震烈度表（European Macroseismic Scale-98，缩写为EMS-98）对受损建筑物进行分类，采用随机森林方法得到总体的预测准确率为67.0%。虽然上述研究实现了利用机器学习方法预测地震损失且得到了不错的准确率，但是仍存在以下几个问题：一是采用的数据样本量有限，难以体现机器学习在数据驱动方面的特性；二是研究区范围通常为城市级别且只针对单一结构类型，缺乏足够区域和建筑物结构类型的泛化能力；三是有的研究仅选取两个破坏等级表示建筑物状态，不能更好地描述建筑物破坏的多种破坏状态；四是最严重破坏等级的准确率有限，有的仅有13%。综上所述，需要进一步利用更加详实的地震破坏资料结合建筑物特性系统地评估地震灾害损失，为震前防御和震后损失预测提供依据（王自法等，2014；赵登科等，2021）。
为了解决上述不足，本文详细整理了2011年3月11日东日本MW9.0地震产生的37万8 037条实际建筑物破坏数据，拟基于随机森林算法设计一个地震损失预测模型。该模型以地震动强度、建筑物基本特征等信息为模型输入，考察其对不同建筑物破坏程度的预测分类性能，比较地震影响因素的重要性，以期为震害预测和风险评估提供一定参考。
1. 数据准备
由原始数据建立训练模型需要以下四个步骤：第一步，采集数据集信息；第二步，处理、合并数据集并对其依据规范进行分类，划分训练集和测试集；第三步，筛选数据中的关键特征，降低模型复杂程度；第四步，使用预处理后的数据集训练模型。
1.1 数据集
1.1.1 建筑物及其损失数据库
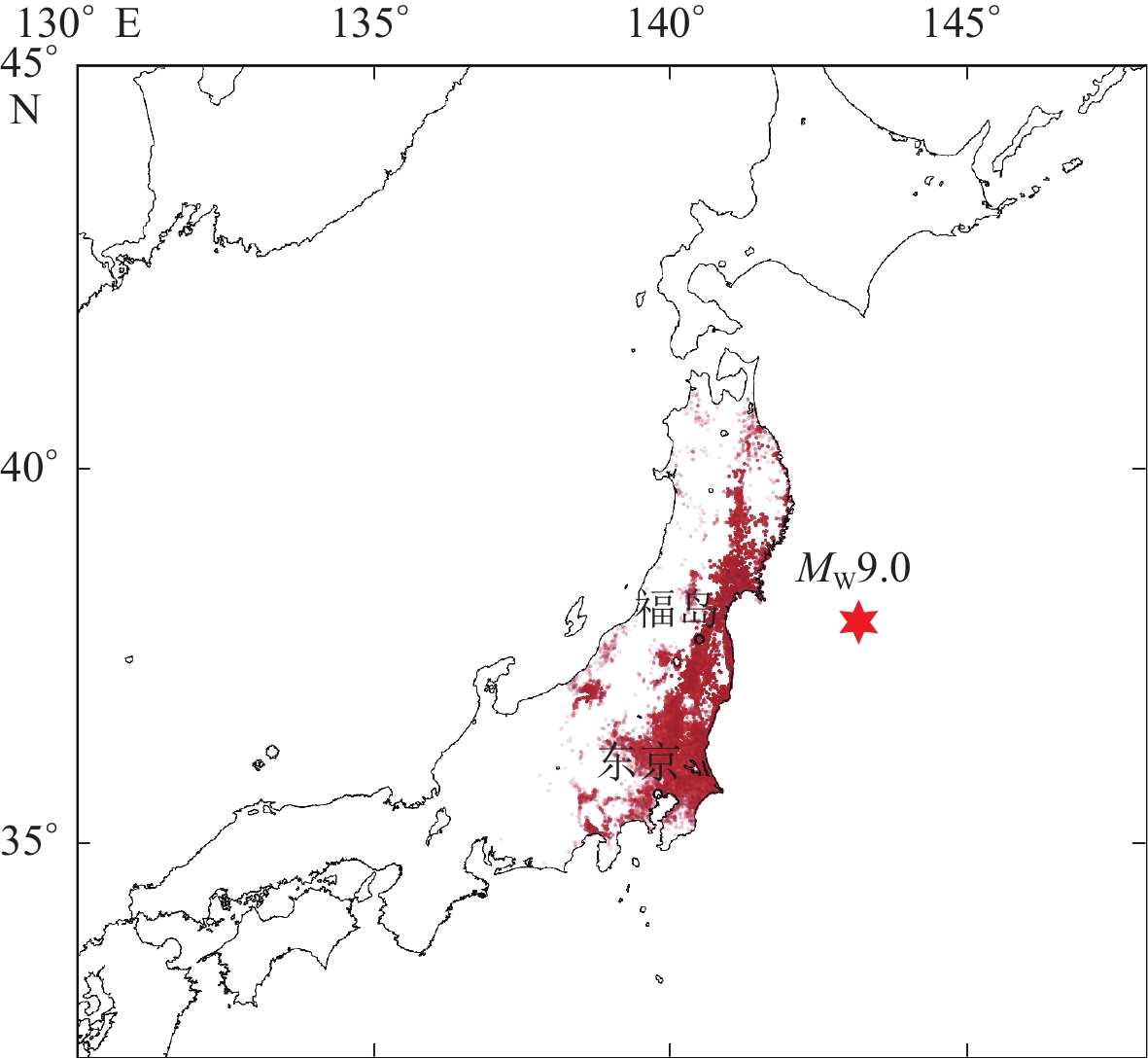
2011年3月11日日本东北海岸地区发生MW9.0地震，该地震造成高达2.8万人死亡和数百万的建筑物受损。美国佛利德斯（Validus）研究中心收集了震后建筑物详细破坏资料，包括建筑物的地区编号、建造年代、层数、结构类型、损失率等建筑物基本特征。本文使用到的建筑物破坏数据分布如图1所示。
![]()
图 1 2011年东日本MW9.0大地震的建筑物损失分布颜色深浅代表地区发生建筑物破坏的数量大小，颜色越深，建筑物破坏数量越多Figure 1. Distribution of building damage resulted from 2011 MW9.0 Tohoku-Oki earthquakeThe shade of the color represents the amount of building damage occurred in the area。The darker the color，the more the building damage1.1.2 地震动参数和vS30
地震损失分析除了考虑建筑物的结构类型、层数、建造年代等特征外，还需考虑地震动强度指标（intensity measure，缩写为IM）和场地相关的因素。在现有研究中，地震动峰值加速度（peak ground acceleration，缩写为PGA）和谱加速度（spectral acceleration，缩写为Sa）是应用最广泛的地震动参数。针对已受损的建筑物，由于无法准确地计算其自振周期，故本研究使用PGA作为地震动参数。直接对目标建筑物场地处的PGA进行估计，PGA估计通常采用基于衰减关系的经验法，因此本文使用Zhao 等（2016a，b）提出的基于日本强震记录的衰减模型。
除此之外，地下30 m深度的平均剪切波速vS30参考Wald和Allen （2007）利用地形坡度法匹配建筑物所在的场地信息。
1.2 数据预处理
常用的数据预处理步骤有：
1） 数据清洗。主要处理数据中存在缺失值、异常值等问题，删除数据中部分特征不明的数据，以提高模型质量。本研究选取的数据不包括以下：① 建造年代、结构类型、屋顶类型等类型不明数据；② 损失率≤5%的建筑物数据。由于建筑物损失率在5%以下时，建筑物修复费用为自付额，建筑物损失均被记录为0%；③ PGA小于0.05g的建筑物数据。
2） 数据合并。数据集包括原始震害调查数据库、建筑物基本信息等，且从不同的来源获得。使用Python数据库中的Merge函数通过数据的邮政编码或者经纬度将两数据进行合并，得到完整的数据集，将其保存至数据库用于后续模型训练。
1.3 分类特征标签的定义及数据集划分
本文中建筑物破坏程度由损失率（damage ratio，缩写为Dr）表示，该指数由美国佛利德斯研究中心统计计算，以百分比形式表示，定义为建筑物损失价值与建筑物总价值的比值。参考美国应用技术协会所发布的地震震害评估标准ATC-13 （McCormack，Rad，1997）将损失率划分为四种破坏等级，即5%＜Dr≤10%时为“轻微破坏” 、10%＜Dr≤30%时为“中等破坏” 、30%＜Dr≤60%时为“严重破坏” 、60%＜Dr≤100%时为“倒塌” ，分别记作数字0，1，2，3，标记的样本用于分类模型训练。四种破坏等级的数据统计见表1。
表 1 依据ATC-13划分的四种破坏等级数据统计Table 1. Statistics on four types of damage levels data according to ATC-13建筑物破坏等级 损失率 记录数量 轻微破坏（0类） 5%＜Dr≤10% 136 334 中等破坏（1类） 10%＜Dr≤30% 178 594 严重破坏（2类） 30%＜Dr≤60% 33 079 倒塌（3类） 60%＜Dr≤100% 30 029 总数量 378 037 机器学习模型的泛化性能主要体现在对于未知数据的预测表现，故本研究将原始数据集划分为训练集和测试集。采用机器学习领域最经典的“八二原则”对原始样本数据进行划分，即从总体样本数据集中选取80%作为训练集，剩余20%的样本数据集作为测试集，这样得到训练集30万2 429组和测试集7万5 608组。
1.4 特征因素选择
在实际记录的地震数据中，一组数据通常包含多个特征，需要从数据中选择相关特征，并考虑输入的特征对模型预测和获取难易程度是否具有决定性影响，其主要目的是为了降低维度，达到降低模型复杂程度的目的。本文参考张风华等（2004）以及张桂欣和孙柏涛（2018），引进以往研究常用的四个研究对象：结构类型、建造年代、建筑用途和层数，此外增加PGA、震中距、vS30等其它特征信息，最终确定11个特征作为模型输入，如表2所示。这些特征综合考虑了地震造成建筑物损失的主要影响因素。
表 2 建筑物数据集的机器学习模型输入特征Table 2. Input features of machine learning model for building datasets类别 影响因素 影响因素的特征描述 计算方法或数据来源 地震
信息PGA 地震动峰值加速度 Zhao等（2 016a，b）公式 震中距 地震震中至建筑物地面距离 Robusto （1 957）计算
两点经纬度距离公式建筑物
信息层数 建筑物层数 数据库 地区编号 47个都道府县 建筑物建造年代 ① 1 867—1910；② 1 911—1 924；③ 1 925—1 987；④ 1 988—2 011 外墙材料类型 ① 混凝土；② 蒸压轻质混凝土；③ 砌块；④ 砂浆；⑤ 抹灰；
⑥ 镶石砖；⑦ 金属板；⑧ 玻璃板；⑨ 石板；⑩ 金属陶瓷；
⑪ 土藏造；⑫ 木制壁板；⑬ 木板建筑物结构类型 ① 木结构；② 混合结构（木和砂浆）；③ 土藏造；④ 砌块；
⑤ 砌体结构；⑥ 钢结构；⑦ 混凝土结构；⑧ 其它柱子材料类型 ① 混凝土柱；② 防火涂层钢结构；③ 钢结构；④ 木框架；
⑤ 双料组合；⑥ 其它屋顶材料类型 ① 混凝土；② 金属板；③ 石板；④ 瓷砖瓦；⑤ 合成树脂；
⑥ 木板；⑦ 茅草建筑物使用用途 ① 住宅；② 其它 场地信息 vS30 地表以下30 m土层的加权平均剪切波速 USGS （2 007） 由于数据集中的建筑物信息如屋顶类型、结构类型、建造年代等特征都属于类别数据，在训练模型前需要将文字数字化，因此使用Python程序数据库函数LabelEncoder编码将每一种特征类别数据转化为数字数据。具体见表2。
2. 机器学习模型
2.1 随机森林模型
随机森林算法是由Breiman （2001）提出，常用于解决回归和分类问题，其基本原理是一种基于决策树和引导聚集算法（Bagging）的集成机器学习方法，将若干个决策树模型并行组合，根据多数投票原则确定最终结果。相较于其它机器学习算法而言，随机森林算法的优势如下：
1） 采用并行计算方法，可提高训练速度，更适用于本文的震害大数据处理；
2） 采用随机节点方式划分属性，可有效减少高维度特征带来的计算量；
3） 基于Booststrap方法随机放回采样，提高了模型的泛化能力，充分考虑了建筑物损失的不确定性；
4） 由多个决策树集成，对异常值不敏感，有利于处理数据中的噪声信息。
此外，很多研究对比了各算法在震害预测方面的表现（Mangalathu et al，2020；Roeslin et al，2020；Ghimire et al，2022；Stojadinović et al，2022），随机森林均表现出较高的预测准确率。因此，本文基于Python语言通过调用Scikit-learn数据库（Pedregosa et al，2011）搭建随机森林分类模型。
2.2 模型评估方法
混淆矩阵是一种评估机器学习预测模型性能的可视化方法，可以直观地观察分类模型的分类性能，将实际类别与预测类别所占的百分比表格化。以二分类问题为例，将预测结果分为真阳性（true positives）、真阴性（ture negatives）、假阳性（false positives）和假阴性（false negatives），具体见表3。在实际研究中，数据有上万条，单纯地计算机器学习模型正确和错误预测结果的样本数目难以评估模型的优劣性，因此利用混淆矩阵方法在统计数据的基础上定义模型的三种度量：精确率（precision）、召回率（recall）和准确率（accuracy），其中精确率是正确分配的预测标签的百分比，召回率是正确分配的实际标签的百分比，准确率是数据样本中所有预测中判断正确（包括正类和负类）的比例，具体表达式如下：
表 3 混淆矩阵Table 3. Confusion matrix混淆矩阵 预测值 正类 负类 真实值 正类 真阳性 假阴性 负类 假阳性 真阴性 $$ 精确率＝\frac{真阳性}{真阳性 ＋ 假阳性}， $$ (1) $$ 召回率＝\frac{真阳性}{真阳性 ＋ 假阴性}， $$ (2) $$ 准确率＝\frac{真阳性＋真阴性}{真阳性＋假阳性＋假阴性＋真阴性}. $$ (3) 3. 模型训练及优化
3.1 模型训练
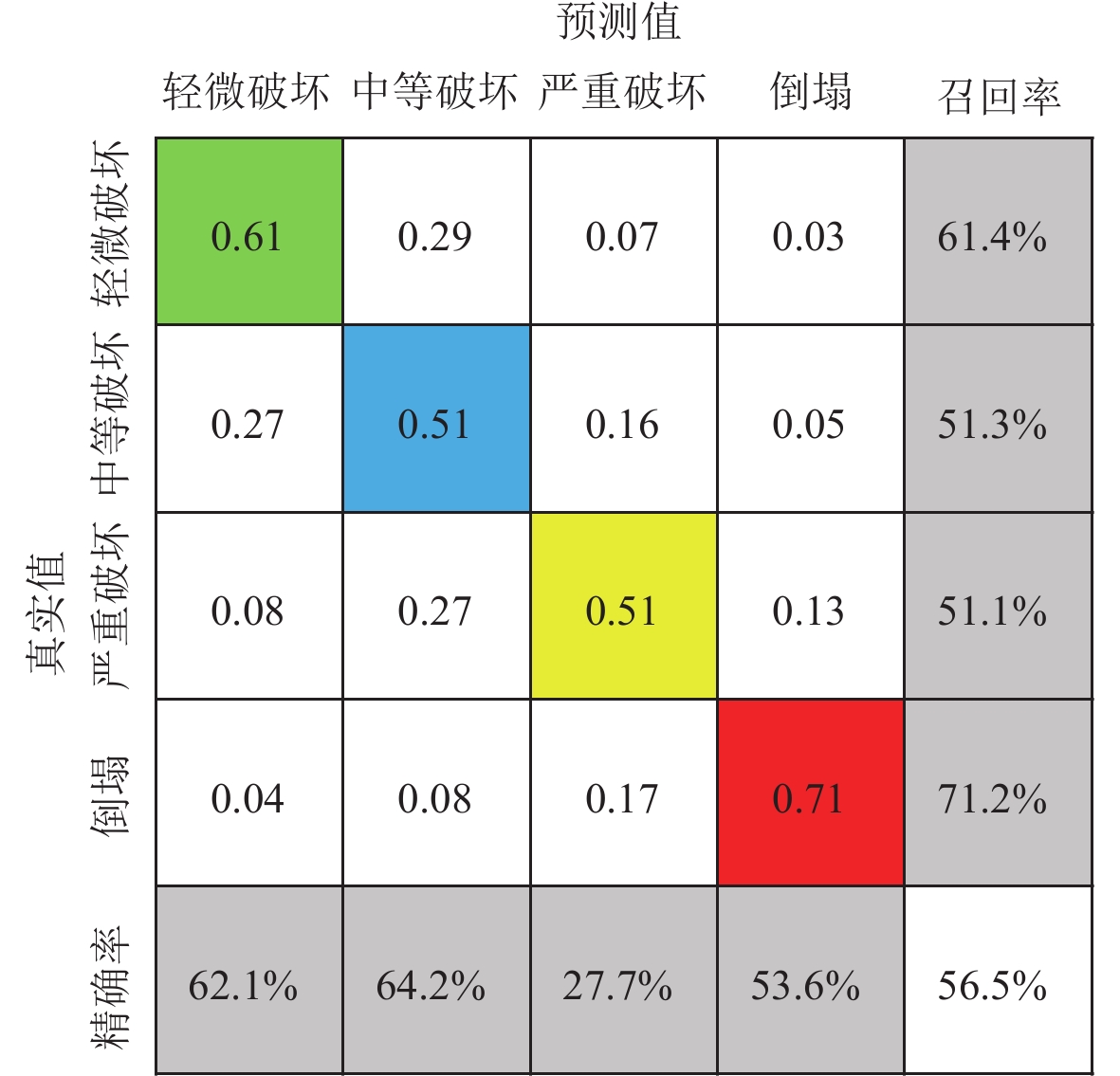
在完成数据集的预处理工作后，将1.4节涉及的11个特征输入随机森林模型中进行训练，所得结果如图2所示。可见：该模型的测试集准确率为56.5%，轻微破坏、中等破坏、严重破坏和倒塌这四种破坏等级测试集的召回率分别为61.4%，51.3%，51.1%和71.2%，精确率分别为62.1%，64.2%，27.7%和53.6%，其中2类（严重破坏）和3类（倒塌）的精确率相对较低，且整体准确率不高，造成这一结果有两个重要原因：第一，一般地震发生后，震灾区受损较轻的建筑物数量往往远多于发生严重破坏的建筑物，这使得震害数据集不平衡，此时准确率并不能很好地体现模型对于少数类样本的分类性能，而数据集中包含大量的多数类样本，因此多数类的准确率在整体准确率中占主导；第二，四种破坏等级的数据集不均衡。从表1看出，0类（轻微破坏）和1类（中等破坏）的数据量分别是其它两类的4倍及以上，精确率定义的是正确分配的预测标签所占的百分比，即使错误预测少数量的0类或1类，也会降低2类、3类的精确率。因此，为了进一步提高模型的分类性能，需要对数据集进行平衡化处理，并对模型进行超参数优化。
3.2 随机森林模型优化
3.2.1 数据集平衡化处理
为了解决上述数据集中出现的不均衡状况，研究人员提出了随机过采样、合成少数类过采样技术（synthetic minority oversampling technique，缩写为SMOTE）（Chawla et al，2002）、随机欠采样等方法。其中，SMOTE方法是通过对每一个少数类样本与其近邻之间的线性插值实现过采样，该方法在解决不平衡数据分类问题上已取得了良好的效果（杨毅等，2017；张天翼，丁立新，2021），因此本文采用SMOTE方法处理数据集中的不均衡问题。
3.2.2 模型的超参数优化
使用机器学习算法的过程中常涉及学习参数和模型的超参数调整，以便输出最优的结果，目前研究中常用的超参数优化方法有网格搜索（Lerman，1980；王健峰，2012）和随机搜索（Bergstra，Bengio，2012；张浩，2018）。网格搜索通过遍历网格内所有点从而确定最优的参数组合，但该方法耗时较长、算力要求高、当参数过多时训练成本呈指数上升。随机搜索通过随机采样参数的组合范围，提高调参效率，但是对于参数较多的机器学习算法，该方法依然效率低、精度差。
为了解决上述两种方法的缺陷，本文选用贝叶斯优化方法（Snoek et al，2012；Shahriari et al，2016）来进行超参数优化。该方法是一种非常高效的优化算法，其性能优于其它全局优化方法（Shahriari et al，2016）。将此方法应用到机器学习算法的超参数优化的具体步骤如下：① 确定决策树个数、决策树最大深度等随机森林模型超参数，将分类准确率作为优化目标函数，即贝叶斯优化的目标是找到恰当的超参数值，使优化目标函数最大；② 利用高斯过程模型拟合目标函数，建立超参数组合和预测目标函数的代理模型，基于该代理模型进一步利用采集函数选择最优的超参数并计算对应的目标函数值，同时根据历史观测值不断地搜索使得目标函数最大，该部分充分考虑了已有的观测值；③ 不断地迭代，直至拟合近似符合条件的目标函数。使用贝叶斯优化方法确定随机森林模型中四个重要的超参数值列于表4。
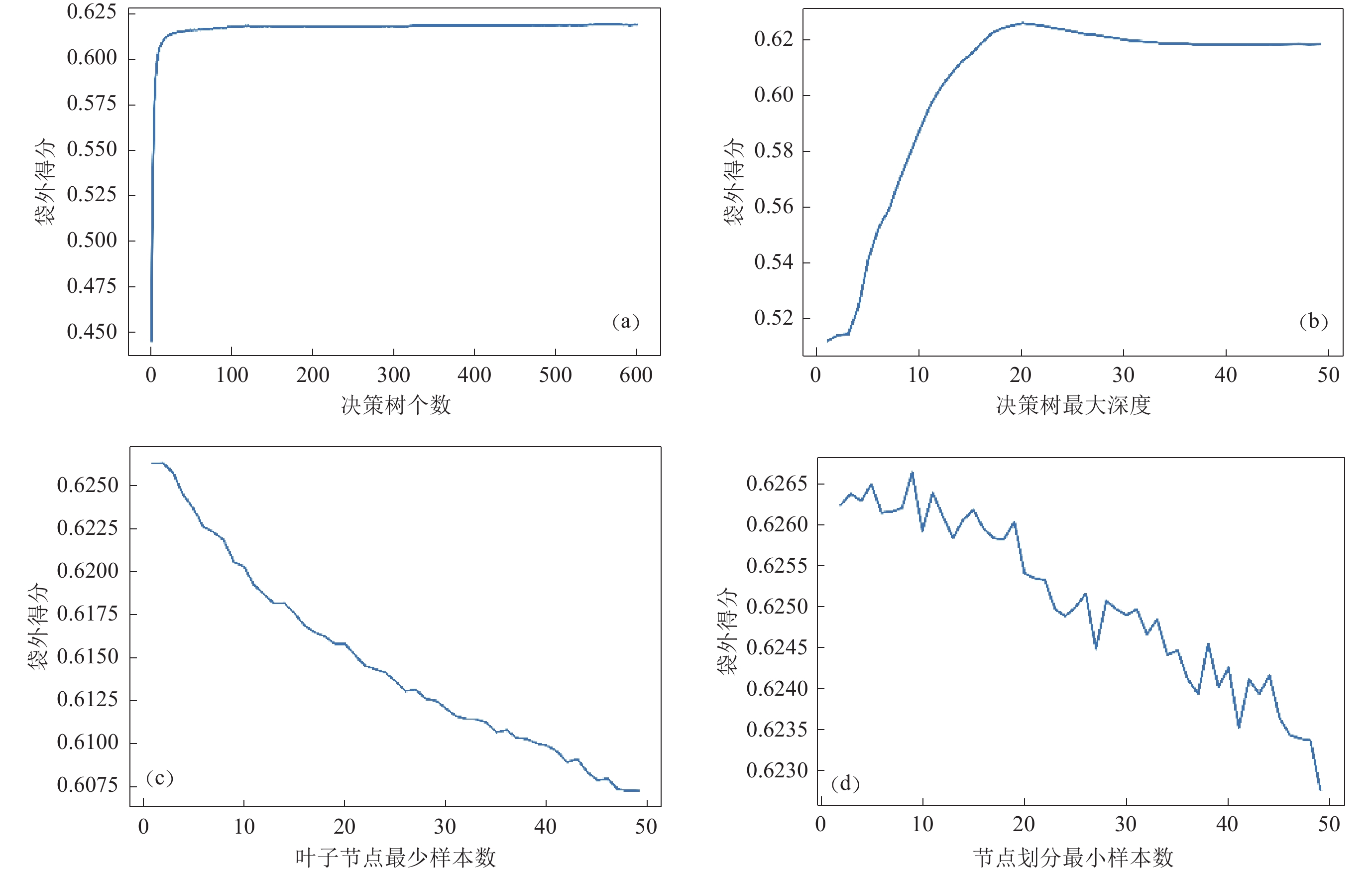
表 4 随机森林模型超参数优化方法对比Table 4. Comparison of hyper-parameter optimization methods for random forest models超参数优化方法 决策树棵数 决策树最大深度 叶子节点最少样本数 节点划分最小样本数 模型准确率 贝叶斯优化 654 48 1 2 68.8% 学习曲线方法 550 20 2 8 65.9% 为进一步论证贝叶斯超参数优化方法的优越性，利用学习曲线（learning curve，缩写为LC）搜索全局最优参数组合，并使用袋外得分评估参数取值的性能。利用学习曲线的调参根据超参数对于模型的影响程度依次进行，具体步骤如下：① 将决策树个数取值区间设置为1—600，步长为1，通过搜索得到该曲线的袋外得分最大值为0.62，对应的决策树为550棵（图3a）；② 在此基础上调整决策树最大深度，其相应的学习曲线如图3b所示，叶子节点最少样本数和节点划分最小样本数的学习曲线分别如图3c和3d所示。最终学习曲线方法优化的超参数列于表4。
![]()
图 3 随机森林四个超参数的学习曲线图（a） 决策树个数；（b） 决策树最大深度；（c） 叶子节点最少样本数；（d） 节点划分最小样本数Figure 3. Learning curves of four hyper-parameters for random forest model（a） Number of estimators；（b） Maximum depth of estimators；（c） Minimum number of samples required to be at a leaf node；（d） Minimum number of samples required to split an internal node综合比较上述贝叶斯优化和学习曲线方法的结果（表4）可知，贝叶斯优化超参数组合可得到更高的模型准确率，因此采用该方法进一步讨论模型的分类性能。
4. 模型结果
4.1 模型预测结果
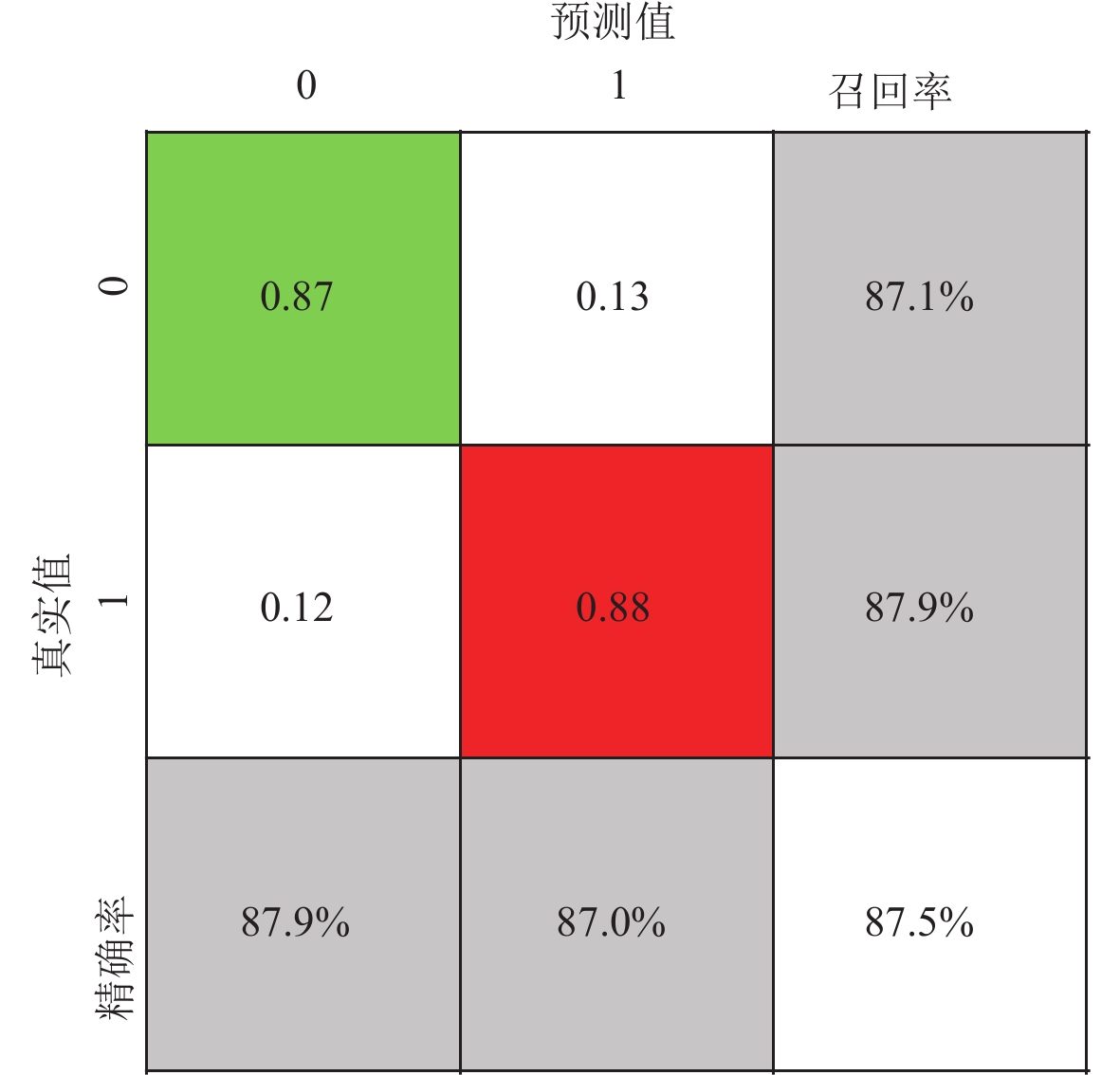
通过对模型采用上述SMOTE方法和贝叶斯优化超参数，可得到使用混淆矩阵评估模型优化后测试集的分类性能结果，如图4所示。
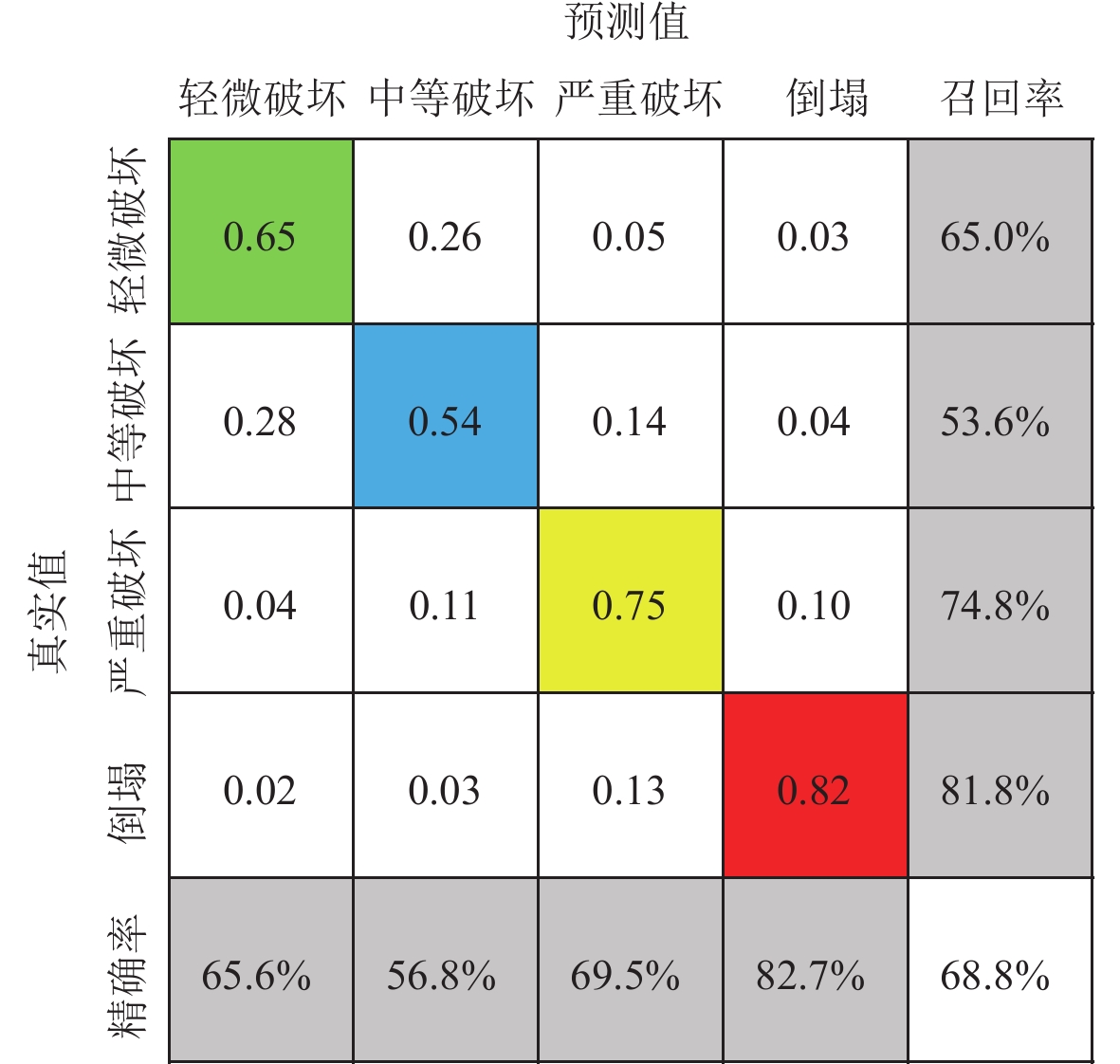
如前所述，测试集是模型未知的数据，用于评估模型的分类性能。图4为随机森林测试集标签分配结果的混淆矩阵，可以看出：对于0类（轻微破坏），召回率为65.0%，精确率为65.6%；对于1类（中等破坏），召回率为53.6%，精确率为56.8%；对于2类（严重破坏），召回率为74.8%，精确率为69.5%；对于3类（倒塌），召回率为81.8%，精确率为82.7%。此外，主对角线方格对应于四种破坏等级的准确率及整体准确率，因此随机森林测试集的整体准确率为68.8%。
通过3.2节对模型的改进，模型的分类性能得到一定的提升，改进后的模型整体准确率提高了12.3%，其中0，1，2和3类这四种分类的召回率分别提高了3.6%，2.3%，23.7%和10.6%。
值得注意的是，1类的召回率仅有53.6%，相对较低，从图4可以观察到1类实际值被错误分配到0类建筑物占1类总样本数量的28.0%。根据统计，损失率介于10%—15%的1类建筑物数量占1类总样本数量的48.1%，此区间下的0类与1类建筑物属性区别度较小，因此这部分的样本容易被错误分配到0类，这在建筑物损失的实际评估中是可以接受的，其原因在于调查中破坏不明显或者需要进一步评估也会降低一级标准，如果机器学习错误地将实际标签分配到跨越两个及以上破坏等级就需要更多关注（Mangalathu et al，2020）。
4.2 影响地震损失特征的重要性分析
随机森林重要性分析的原理是获取每个特征在决策树的贡献值，取其平均值，然后比较各个特征平均贡献值的大小，通常采用袋外误差率来评估特征重要性。特征A的重要性可表示为：
$$ I_{A} ＝ \frac{1}{N}\sum\limits_{i ＝ 1}^1 {|{{{E}}_2}－ {E_1}|} ，$$ (4) 式中：N为决策树数目，E1为每棵决策树对应袋外数据的预测误差值，E2为对袋外数据随机加入特征A的噪声后重新计算所得的预测误差值。
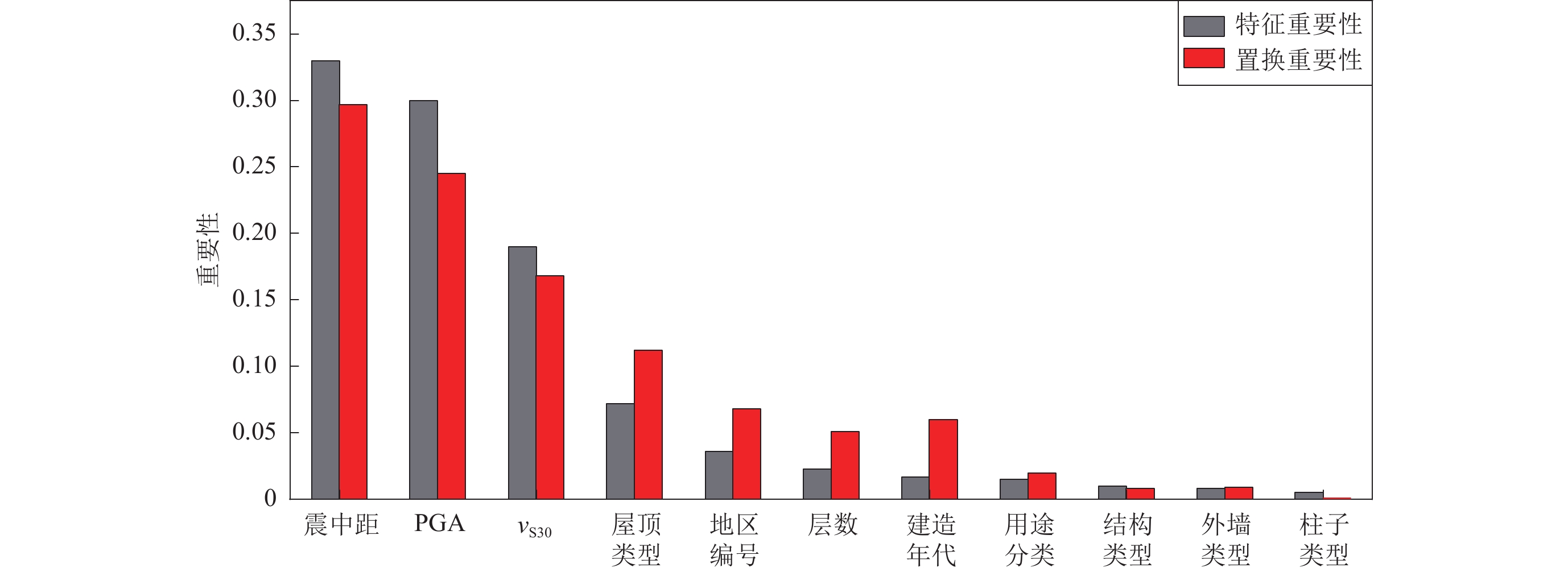
本节在3.2节优化模型基础上采用随机森林特征重要性（feature importance，缩写为FI）输出各影响因素的重要性排序，结果如图5所示，可见：影响建筑物损失的主要因素的重要性排序为震中距＞PGA＞vS30＞屋顶类型＞地区编号＞层数＞建造年代＞用途分类＞结构类型＞外墙类型＞柱子类型。
![]()
图 5 特征重要性和置换重要性排序方法比较Figure 5. Comparison of feature importance and permutation importance ranking methods为了进一步验证特征重要性方法的重要性排序的可靠性，下面将基于3.2节优化模型采用eli5数据库下的置换重要性（permutation importance，缩写为PI）进行11个特征的重要性排序。置换重要性方法是在模型训练结束后，将测试集某一列数据的顺序打乱，根据评估模型性能来判断该特征对应模型结果的重要性程度。结果如图5所示，影响建筑物损失的主要因素的重要性排序为震中距＞PGA＞vs30＞屋顶类型＞地区编号＞建造年代＞层数＞用途分类＞外墙类型 ＞结构类型＞柱子类型。
综合上述两种重要性排序方法结果对比印证可得：采用FI和PI方法论证地震损失的主要影响因素的重要性排序是相同的，最重要的因素为震中距、PGA和vS30，且其重要性远大于其它特征；后六个特征排序略有差异，其中层数和建造年代、结构类型和外墙类型发生次序互换。
4.3 模型适用性
为了进一步提升模型预测精度，提高震后及时救援工作质量，参考Tesfamariam和Liu （2010）中考虑生命安全的性能分类，将轻微破坏、中等破坏等级划分为0类，将严重破坏、倒塌等级划分为1类，在3.2.2节超参数不变的情况下，混沌矩阵如图6所示。结果显示：模型测试集的准确率达到87.5%，其中0类（轻微破坏、中等破坏）和1类（严重破坏、倒塌）的召回率分别为87.1%和87.9%。相较于Suryanita等（2017）和Mansourdehghan等（2022）的结果，本节模型所得的考虑生命安全的性能分类准确率更高。
收集近年已发表的研究方向类似的文献比较本文模型的结果优劣。现有研究数据分为两类：数值模拟和震后实地调查。部分基于数值模拟数据应用于地震损失预测的结果较好，例如：Yuan等（2022）开发了一个多地震动参数输入的人工神经网络分类器，其总体精度为67.5%；Hwang等（2021）基于四层和八层钢筋混凝土框架建筑物倒塌状态建立了二分类模型，使用六种机器学习方法识别建筑物是否发生倒塌，预测精度均达到90%以上。但上述研究从分类类型、结构类型、建筑物多方面多样化等均逊色于实地调查的研究数据。相对而言考虑震后建筑物的真实反应，研究更有意义。表5列举了基于实地调查数据的震害预测相关研究，对比可知：从分类类型、研究数据、最严重破坏状态准确率、模型整体准确率等五个方面综合考察，本文模型结果相较已有结果均有不同程度的提升。
表 5 基于实地调查数据的震害预测研究结果比较Table 5. Comparison of seismic damage prediction research results based on field survey data来源 模型类型 分类
类型研究数据 最严重破坏
状态准确率模型
准确率Harirchian等（2 021b） 极端随机树 三分类 2 016年厄瓜多尔地震，172座受损钢筋混凝土建筑物 55.0% 70.2% 三分类 2 010年海地地震，145座受损钢筋混凝土建筑物 41.2% 58.5% 四分类 2 017年韩国浦项市地震，74座受损建筑物 50.0% 60.0% Harirchian等（2 020c） 支持向量机 三分类 2 016年厄瓜多尔地震，171座受损钢筋混凝土建筑物 54.0% 60.0% 三分类 2 010年海地地震，142座受损钢筋混凝土建筑物 54.0% 68.0% 四分类 2 015年尼泊尔地震，138座受损钢筋混凝土建筑物 33.0% 67.0% 四分类 2 017年韩国浦项市地震，67座受损建筑物 2 0.0% 48.0% Harirchian等（2 020a） 多层感知器 五分类 1 999年土耳其迪兹杰地震，484座受损建筑物 71.4% 52.0% Harirchian等（2 020b） 支持向量机 五分类 1 999年土耳其迪兹杰地震，484座受损建筑物 54.5% 52.0% Mangalathu和Burton （2 019） 长短期记忆网络 三分类 2 014年美国纳帕南部地震， 3423 座受损建筑物63.0% 86.0% Mangalathu等（2 020） 随机森林 三分类 2 014年美国纳帕南部地震， 2276 座受损建筑物13.0% 66.0% Roeslin等（ 2020） 随机森林 二分类 2 017年墨西哥普埃布拉地震，237座受损建筑物 78.0% 67.0% Stojadinović等（2 022） 随机森林 五分类 2 010年塞尔维亚克拉列沃地震，1 979座受损建筑物 30.0% 85.0% Ghimire等（2 022） 随机森林 三分类 2 015年尼泊尔地震，76.2万座受损建筑物 70.0% 64.0% 本文 随机森林 四分类 2 011年东日本大地震，37.8万座受损建筑物 81.8% 68.8% 二分类 88.0% 87.5% 5. 讨论与结论
本文应用大量详细的地震损失资料，利用随机森林算法系统全面地研究了2011年3月11日东日本MW9.0地震的建筑物损失，分析了11个影响建筑物损失的因素的重要性，实现了地震损失预测与机器学习的交叉应用，极大地改善了现有研究应用于建筑物损失预测中数据受限、研究地域泛化能力缺乏、研究建筑物属性多方面多样化缺乏、破坏等级划分不精细和最严重破坏状态精度低的问题。
本文探讨使用机器学习算法来预测建筑物损失的有效性。随机森林算法可有效地应用于震后快速损失预测评估，通过采用SMOTE方法和贝叶斯优化超参数，模型整体准确率可达68.8%，相比较初始模型提高12.3%，轻微破坏、中等破坏、严重破坏和倒塌这四种破坏等级召回率分别为65.0%，53.6%，74.8%和81.8%，分别提升了3.6%，2.3%，23.7%和10.6%。
为了对比不同全局超参数优化方法的性能表现，本研究采用贝叶斯优化和学习曲线分别对模型进行调参，结果显示经过贝叶斯优化后模型精度更高。
采用不同原理的特征重要性和置换重要性方法相互印证了11个特征的重要性，其中震中距、PGA和vS30是影响建筑物损失最主要的因素。
在考虑生命安全性能情况下，将模型预测目标转换为二分类，模型整体准确率达到87.5%，保证模型精度的同时，进一步提高了模型的适用性和震后及时救援工作质量。
本文将机器学习方法应用于震害预测领域，有效地进行了地震损失评估和数据特征的提取，进一步分析影响地震的重要因素，结果显示基于大数据方法下利用机器学习进行地震损失预测的巨大潜力，下阶段将收集其它国家地区的详细样本数据以验证本模型的适用性；增加多次地震事件的样本数据，以进一步增加模型的泛化能力；通过增加更多的数据维度作为模型训练，提高震害预测精确度。
-
![]()
图 1 2011年东日本MW9.0大地震的建筑物损失分布
颜色深浅代表地区发生建筑物破坏的数量大小，颜色越深，建筑物破坏数量越多
Figure 1. Distribution of building damage resulted from 2011 MW9.0 Tohoku-Oki earthquake
The shade of the color represents the amount of building damage occurred in the area。The darker the color，the more the building damage
![]()
图 3 随机森林四个超参数的学习曲线图
（a） 决策树个数；（b） 决策树最大深度；（c） 叶子节点最少样本数；（d） 节点划分最小样本数
Figure 3. Learning curves of four hyper-parameters for random forest model
（a） Number of estimators；（b） Maximum depth of estimators；（c） Minimum number of samples required to be at a leaf node；（d） Minimum number of samples required to split an internal node
![]()
图 5 特征重要性和置换重要性排序方法比较
Figure 5. Comparison of feature importance and permutation importance ranking methods
表 1 依据ATC-13划分的四种破坏等级数据统计
Table 1 Statistics on four types of damage levels data according to ATC-13
建筑物破坏等级 损失率 记录数量 轻微破坏（0类） 5%＜Dr≤10% 136 334 中等破坏（1类） 10%＜Dr≤30% 178 594 严重破坏（2类） 30%＜Dr≤60% 33 079 倒塌（3类） 60%＜Dr≤100% 30 029 总数量 378 037 
下载: 导出CSV
表 2 建筑物数据集的机器学习模型输入特征
Table 2 Input features of machine learning model for building datasets
类别 影响因素 影响因素的特征描述 计算方法或数据来源 地震
信息PGA 地震动峰值加速度 Zhao等（2 016a，b）公式 震中距 地震震中至建筑物地面距离 Robusto （1 957）计算
两点经纬度距离公式建筑物
信息层数 建筑物层数 数据库 地区编号 47个都道府县 建筑物建造年代 ① 1 867—1910；② 1 911—1 924；③ 1 925—1 987；④ 1 988—2 011 外墙材料类型 ① 混凝土；② 蒸压轻质混凝土；③ 砌块；④ 砂浆；⑤ 抹灰；
⑥ 镶石砖；⑦ 金属板；⑧ 玻璃板；⑨ 石板；⑩ 金属陶瓷；
⑪ 土藏造；⑫ 木制壁板；⑬ 木板建筑物结构类型 ① 木结构；② 混合结构（木和砂浆）；③ 土藏造；④ 砌块；
⑤ 砌体结构；⑥ 钢结构；⑦ 混凝土结构；⑧ 其它柱子材料类型 ① 混凝土柱；② 防火涂层钢结构；③ 钢结构；④ 木框架；
⑤ 双料组合；⑥ 其它屋顶材料类型 ① 混凝土；② 金属板；③ 石板；④ 瓷砖瓦；⑤ 合成树脂；
⑥ 木板；⑦ 茅草建筑物使用用途 ① 住宅；② 其它 场地信息 vS30 地表以下30 m土层的加权平均剪切波速 USGS （2 007）
下载: 导出CSV
表 4 随机森林模型超参数优化方法对比
Table 4 Comparison of hyper-parameter optimization methods for random forest models
超参数优化方法 决策树棵数 决策树最大深度 叶子节点最少样本数 节点划分最小样本数 模型准确率 贝叶斯优化 654 48 1 2 68.8% 学习曲线方法 550 20 2 8 65.9%
下载: 导出CSV
表 5 基于实地调查数据的震害预测研究结果比较
Table 5 Comparison of seismic damage prediction research results based on field survey data
来源 模型类型 分类
类型研究数据 最严重破坏
状态准确率模型
准确率Harirchian等（2 021b） 极端随机树 三分类 2 016年厄瓜多尔地震，172座受损钢筋混凝土建筑物 55.0% 70.2% 三分类 2 010年海地地震，145座受损钢筋混凝土建筑物 41.2% 58.5% 四分类 2 017年韩国浦项市地震，74座受损建筑物 50.0% 60.0% Harirchian等（2 020c） 支持向量机 三分类 2 016年厄瓜多尔地震，171座受损钢筋混凝土建筑物 54.0% 60.0% 三分类 2 010年海地地震，142座受损钢筋混凝土建筑物 54.0% 68.0% 四分类 2 015年尼泊尔地震，138座受损钢筋混凝土建筑物 33.0% 67.0% 四分类 2 017年韩国浦项市地震，67座受损建筑物 2 0.0% 48.0% Harirchian等（2 020a） 多层感知器 五分类 1 999年土耳其迪兹杰地震，484座受损建筑物 71.4% 52.0% Harirchian等（2 020b） 支持向量机 五分类 1 999年土耳其迪兹杰地震，484座受损建筑物 54.5% 52.0% Mangalathu和Burton （2 019） 长短期记忆网络 三分类 2 014年美国纳帕南部地震， 3423 座受损建筑物63.0% 86.0% Mangalathu等（2 020） 随机森林 三分类 2 014年美国纳帕南部地震， 2276 座受损建筑物13.0% 66.0% Roeslin等（ 2020） 随机森林 二分类 2 017年墨西哥普埃布拉地震，237座受损建筑物 78.0% 67.0% Stojadinović等（2 022） 随机森林 五分类 2 010年塞尔维亚克拉列沃地震，1 979座受损建筑物 30.0% 85.0% Ghimire等（2 022） 随机森林 三分类 2 015年尼泊尔地震，76.2万座受损建筑物 70.0% 64.0% 本文 随机森林 四分类 2 011年东日本大地震，37.8万座受损建筑物 81.8% 68.8% 二分类 88.0% 87.5%
下载: 导出CSV
-
鲍跃全,李惠. 2019. 人工智能时代的土木工程[J]. 土木工程学报,52(5):1–11. Bao Y Q,Li H. 2019. Artificial intelligence for civil engineering[J]. China Civil Engineering Journal,52(5):1–11 (in Chinese).
孙柏涛,胡少卿. 2005. 基于已有震害矩阵模拟的群体震害预测方法研究[J]. 地震工程与工程振动,25(6):102–108. Sun B T,Hu S Q. 2005. A method for earthquake damage prediction of building group based on existing earthquake damage matrix[J]. Earthquake Engineering and Engineering Vibration,25(6):102–108 (in Chinese).
王健峰. 2012. 基于改进网格搜索法SVM参数优化的说话人识别研究[D]. 哈尔滨:哈尔滨工程大学:25−26. Wang J F. 2012. Study on Speaker Recognition Based on Improved Grid Search Parameters Optimization Algorithm of SVM[D]. Harbin:Harbin Engineering University:25−26 (in Chinese).
王自法,Park S,Lee S,崔凯. 2014. 提高地震灾害损失估计精度的几点研究[J]. 地震工程与工程振动,34(4):110–114. Wang Z F,Park S,Lee S,Cui K. 2014. Quantification improvement of earthquake loss estimation[J]. Earthquake Engineering and Engineering Dynamics,34(4):110–114 (in Chinese).
隗永刚,蒋长胜. 2021. 人工智能技术在地震减灾应用中的研究进展[J]. 地球物理学进展,36(2):516–524. doi: 10.6038/pg2021EE0164 Wei Y G,Jiang C S. 2021. Research progress of artificial intelligence technology in the application of earthquake disaster reduction[J]. Progress in Geophysics,36(2):516–524 (in Chinese).
杨旭,李永华,盖增喜. 2021. 机器学习在地震学中的应用进展[J]. 地球与行星物理论评,52(1):76–88. Yang X,Li Y H,Gai Z X. 2021. Machine learning and its application in seismology[J]. Reviews of Geophysics and Planetary Physics,52(1):76–88 (in Chinese).
杨毅,卢诚波,徐根海. 2017. 面向不平衡数据集的一种精化Borderline-SMOTE方法[J]. 复旦学报(自然科学版),56(5):537–544. Yang Y,Lu C B,Xu G H. 2017. A refined borderline-SMOTE method for imbalanced data set[J]. Journal of Fudan University (Natural Science),56(5):537–544 (in Chinese).
于红梅,许建东,张素灵,潘波. 2006. 基于集集地震的建筑物易损性统计分析[J]. 防灾科技学院学报,8(4):17–20. doi: 10.3969/j.issn.1673-8047.2006.04.004 Yu H M,Xu J D,Zhang S L,Pan B. 2006. The statistical analysis of building vulnerability research on Jiji earthquake[J]. Journal of Institute of Disaster Prevention,8(4):17–20 (in Chinese).
张风华,谢礼立,范立础. 2004. 城市建构筑物地震损失预测研究[J]. 地震工程与工程振动,24(3):12–20. doi: 10.3969/j.issn.1000-1301.2004.03.002 Zhang F H,Xie L L,Fan L C. 2004. A study on disaster loss prediction caused by damaged structures under earthquake[J]. Earthquake Engineering and Engineering Vibration,24(3):12–20 (in Chinese).
张桂欣,孙柏涛. 2018. 基于模糊层次分析的建筑物单体震害预测方法研究[J]. 工程力学,35(12):185–193. Zhang G X,Sun B T. 2018. Seismic damage prediction for a single building based on a fuzzy analytical hierarchy approach[J]. Engineering Mechanics,35(12):185–193 (in Chinese).
张浩. 2018. 自动化特征工程与参数调整算法研究[D]. 成都:电子科技大学:26. Zhang H. 2018. Research of Automatic Feature Engineering and Parameter Adjustment Algorithm[D]. Chengdu:University of Electronic Science and Technology of China:26 (in Chinese).
张天翼,丁立新. 2021. 一种基于SMOTE的不平衡数据集重采样方法[J]. 计算机应用与软件,38(9):273–279. Zhang T Y,Ding L X. 2021. A new resampling method based on SMOTE for imbalanced data set[J]. Computer Applications and Software,38(9):273–279 (in Chinese).
赵登科,王自法,刘渊,仝文博. 2021. 基于新西兰实际震害资料的地震损失不确定性分析[J]. 地震工程与工程振动,41(2):84–95. Zhao D K,Wang Z F,Liu Y,Tong W B. 2021. Earthquake loss uncertainty based on detailed loss data in New Zealand[J]. Earthquake Engineering and Engineering Dynamics,41(2):84–95 (in Chinese).
Applied Technology Council. 1985. Earthquake Damage Evaluation Data for California[M]. Redwood City:Applied Technology Council:167−219.
Bergstra J,Bengio Y. 2012. Random search for hyper-parameter optimization[J]. J Machine Learn Res,13:281–305.
Breiman L. 2001. Random forests[J]. Mach Learn,45(1):5–32. doi: 10.1023/A:1010933404324
Calvi G M,Pinho R,Magenes G,Bommer J J,Restrepo-Vélez L F,Crowley H. 2006. Development of seismic vulnerability assessment methodologies over the past 30 years[J]. ISET J Earthq Technol,43(3):75–104.
Chawla N V,Bowyer K W,Hall L O,Kegelmeyer W P. 2002. SMOTE:Synthetic minority over-sampling technique[J]. J Artif Intell Res,16:321–357. doi: 10.1613/jair.953
Ghimire S,Guéguen P,Giffard-Roisin S,Schorlemmer D. 2022. Testing machine learning models for seismic damage prediction at a regional scale using building-damage dataset compiled after the 2015 Gorkha Nepal earthquake[J]. Earthq Spectra,38(4):2970–2993. doi: 10.1177/87552930221106495
Harirchian E,Lahmer T,Rasulzade S. 2020a. Earthquake hazard safety assessment of existing buildings using optimized multi-layer perceptron neural network[J]. Energies,13(8):2060. doi: 10.3390/en13082060
Harirchian E,Lahmer T,Kumari V,Jadhav K. 2020b. Application of support vector machine modeling for the rapid seismic hazard safety evaluation of existing buildings[J]. Energies,13(13):3340. doi: 10.3390/en13133340
Harirchian E,Kumari V,Jadhav K,Raj Das R,Rasulzade S,Lahmer T. 2020c. A machine learning framework for assessing seismic hazard safety of reinforced concrete buildings[J]. Appl Sci,10(20):7153. doi: 10.3390/app10207153
Harirchian E,Hosseini S E A,Jadhav K,Kumari V,Rasulzade S,Işık E,Wasif M,Lahmer T. 2021a. A review on application of soft computing techniques for the rapid visual safety evaluation and damage classification of existing buildings[J]. J Build Eng,43:102536. doi: 10.1016/j.jobe.2021.102536
Harirchian E,Kumari V,Jadhav K,Rasulzade S,Lahmer T,Raj Das R. 2021b. A synthesized study based on machine learning approaches for rapid classifying earthquake damage grades to RC buildings[J]. Appl Sci,11(16):7540. doi: 10.3390/app11167540
Hwang S H,Mangalathu S,Shin J,Jeon J S. 2021. Machine learning-based approaches for seismic demand and collapse of ductile reinforced concrete building frames[J]. J Build Eng,34:101905. doi: 10.1016/j.jobe.2020.101905
Lerman P M. 1980. Fitting segmented regression models by grid search[J]. J R Stat Soc Series C Appl Stat,29(1):77–84.
Mangalathu S,Burton H V. 2019. Deep learning-based classification of earthquake-impacted buildings using textual damage descriptions[J]. Int J Disast Risk Reduct,36:101111. doi: 10.1016/j.ijdrr.2019.101111
Mangalathu S,Sun H,Nweke C C,Yi Z X,Burton H V. 2020. Classifying earthquake damage to buildings using machine learning[J]. Earthq Spectra,36(1):183–208. doi: 10.1177/8755293019878137
Mansourdehghan S,Dolatshahi K M,Asjodi A H. 2022. Data-driven damage assessment of reinforced concrete shear walls using visual features of damage[J]. J Build Eng,53:104509. doi: 10.1016/j.jobe.2022.104509
McCormack T C,Rad F N. 1997. An earthquake loss estimation methodology for buildings based on ATC-13 and ATC-21[J]. Earthq Spectra,13(4):605–621. doi: 10.1193/1.1585971
Miyakoshi J,Hayashi Y,Tamura K,Fukuwa N. 1997. Damage ratio functions of buildings using damage data of the 1995 Hyogo-Ken Nanbu earthquake[C]//Proceedings of the 7th International Conference on Structural Safety and Reliability. Kyoto:International Association for Structural Safety and Reliability:349−354.
Pedregosa F,Varoquaux G,Gramfort A,Michel V,Thirion B,Grisel O,Blondel M,Prettenhofer P,Weiss R,Dubourg V,Vanderplas J,Passos A,Cournapeau D,Brucher M,Perrot M,Duchesnay E. 2011. Scikit-learn:Machine learning in Python[J]. J Mach Learn Res,12:2825–2830.
Robusto C C. 1957. The Cosine-Haversine formula[J]. Am Math Mon,64(1):38–40.
Roeslin S,Ma Q,Juárez-Garcia H,Gómez-Bernal A,Wicker J,Wotherspoon L. 2020. A machine learning damage prediction model for the 2017 Puebla-Morelos,Mexico,earthquake[J]. Earthq Spectra,36(S2):314–339.
Shahriari B,Swersky K,Wang Z Y,Adams R P,De Freitas N. 2016. Taking the human out of the loop:A review of Bayesian optimization[J]. Proc IEEE,104(1):148–175. doi: 10.1109/JPROC.2015.2494218
Singhal A,Kiremidjian A S. 1996. Method for probabilistic evaluation of seismic structural damage[J]. J Structural Eng,122(12):1459–1467. doi: 10.1061/(ASCE)0733-9445(1996)122:12(1459)
Snoek J,Larochelle H,Adams R P. 2012. Practical Bayesian optimization of machine learning algorithms[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe:Curran Associates Inc.:2951−2959.
Stojadinović Z,Kovačević M,Marinković D,Stojadinović B. 2022. Rapid earthquake loss assessment based on machine learning and representative sampling[J]. Earthq Spectra,38(1):152–177. doi: 10.1177/87552930211042393
Suryanita R,Maizir H,Yuniarto E,Zulfakar M,Jingga H. 2017. Damage level prediction of reinforced concrete building based on earthquake time history using artificial neural network[C]//The 6th International Conference of Euro Asia Civil Engineering Forum. Seoul:Euro Asia Civil Engineering Forum, 138 :02024.
Tesfamariam S,Liu Z. 2010. Earthquake induced damage classification for reinforced concrete buildings[J]. Struct Saf,32(2):154–164. doi: 10.1016/j.strusafe.2009.10.002
USGS. 2007. vS30 models and data[DB/OL]. [2022-08-01]. https://earthquake.usgs.gov/data/vs30/.
Wald D J,Allen T I. 2007. Topographic slope as a proxy for seismic site conditions and amplification[J]. Bull Seismol Soc Am,97(5):1379–1395. doi: 10.1785/0120060267
Whitman R V,Reed J W,Hong S T. 1973. Earthquake damage probability matrices[C]//Proceedings of the Fifth World Conference on Earthquake Engineering. Rome:Palazzo dei Congressi (EUR):2531−2540.
Yuan X Z,Chen G D,Jiao P,Li L J,Han J,Zhang H B. 2022. A neural network-based multivariate seismic classifier for simultaneous post-earthquake fragility estimation and damage classification[J]. Eng Struct,255:113918. doi: 10.1016/j.engstruct.2022.113918
Zhao J X,Liang X,Jiang F,Xing H,Zhu M,Hou R B,Zhang Y B,Lan X W,Rhoades D A,Irikura K,Fukushima Y,Somerville P G. 2016a. Ground-motion prediction equations for subduction interface earthquakes in Japan using site class and simple geometric attenuation functions[J]. Bull Seismol Soc Am,106(4):1518–1534. doi: 10.1785/0120150034
Zhao J X,Zhou S L,Zhou J,Zhao C,Zhang H,Zhang Y B,Gao P J,Lan X W,Rhoades D,Fukushima Y,Somerville P G,Irikura K. 2016b. Ground‐motion prediction equations for shallow crustal and upper-mantle earthquakes in Japan using site class and simple geometric attenuation functions[J]. Bull Seismol Soc Am,106(4):1552–1569. doi: 10.1785/0120150063
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 244
- HTML全文浏览量: 74
- PDF下载量: 61
- 被引次数: 1
